中小跨径桥梁座式桥台抗震性能参数敏感性分析

杨宝刚, 李永庆, 张 玥, 宋 飞

(1. 西安科技大学 建筑与土木工程学院, 陕西 西安 710054;2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710068)

0 引言

桥台作为衔接桥梁结构与公路工程的构筑物,是地震时桥梁结构中的薄弱环节[1]。在历次地震中,桥台破坏凸显严重,其主要原因是桥台背墙与主梁发生碰撞引起台后填土失效,从而导致桥台发生滑移、倾斜等破坏。桥台的破坏不仅会导致自身丧失功能,而且还会诱发落梁、桥梁垮塌等严重震害。因此考虑上部结构—桥台—土体相互作用已成为桥梁抗震分析的趋势,自20世纪90年代开始,美国学者采用台帽与背墙分离的结构对上部结构—桥台—土体系统进行了一系列大尺寸拟静力试验与理论研究[2-4],基于这些研究成果,CALTRANS抗震设计标准将背墙纵向挤压回填土的力-位移关系进行双折线简化。随后许多学者[5-9]在进行桥梁整体抗震分析时,采用CALTRANS抗震设计标准[10]中反映台后填土力学性能的非线性弹簧来模拟上部结构—桥台—土体相互作用。

然而以上研究大部分所采用模拟桥台的方法忽视了桥台自身强度的贡献,刘洋[11]初步探索桥台强度对连续梁桥抗震分析的影响,发现考虑桥台强度和不考虑桥台强度对主梁位移及桥墩位移延性影响较大,并建议在桥梁抗震分析时考虑桥台强度。CALTRANS标准将桥台分为整体式桥台和座式桥台,其中座式桥台在我国应用较为广泛,本文以某中小跨径梁桥的座式桥台为背景,采用正交数值模拟试验方法,选取峰值位移、峰值荷载、平均刚度以及位移延性系数作为桥台抗震性能评价指标,研究桥台构造参数变化对桥台的抗震性能影响规律,为后期的桥台抗震研究提供参考。

1 工程背景

本文以某3跨连续梁桥为依据,桥跨布置为3×30 m。上部结构由4片小箱梁组成,桥梁宽度布置为净-15+2×0.5 m护轮带;桥梁下部结构采用柱式墩;两侧均为座式桥台。两侧桥台上部结构构造基本相同,图1为一侧桥台构造图,图2是桥台配筋图。两侧桥台采用C30混凝土,HRB335钢筋,台后回填透水性好的砂土,压实度大于95%。

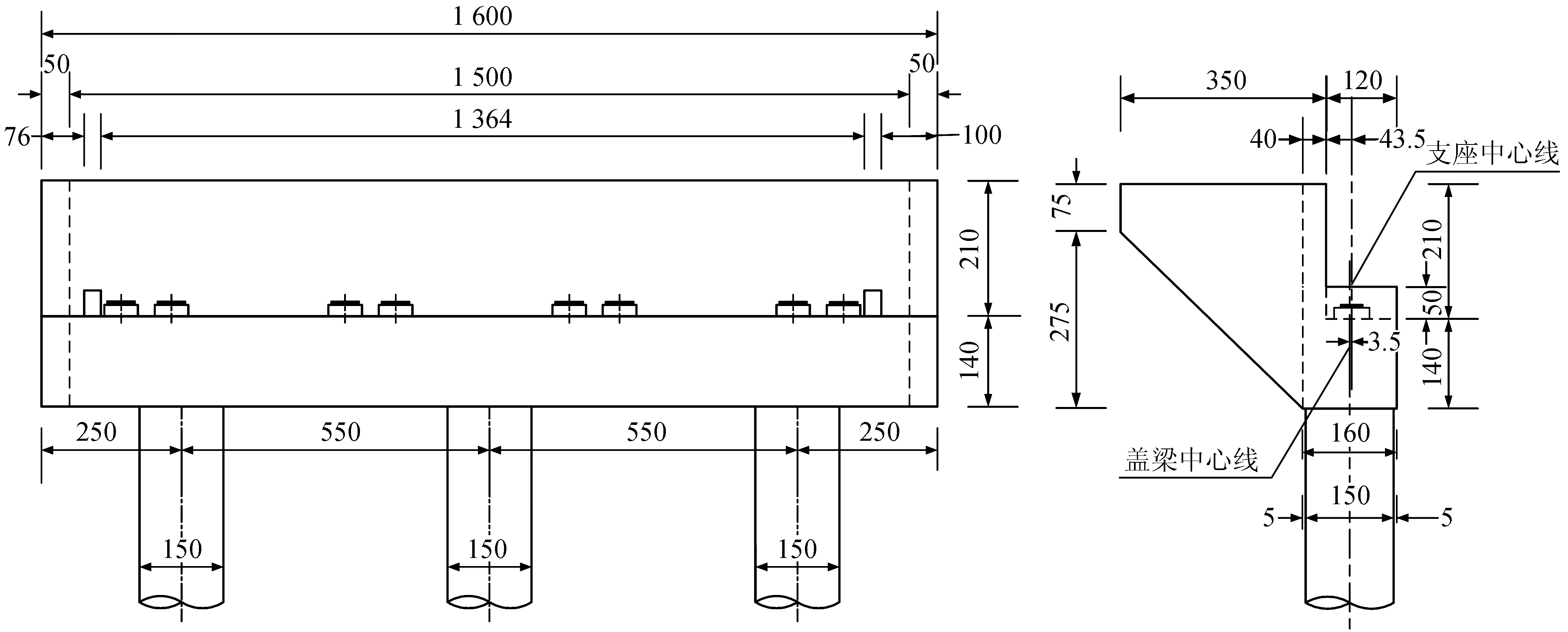
图1 座式桥台构造图(单位:cm)Fig.1 Structure of seat abutment (Unit:cm)

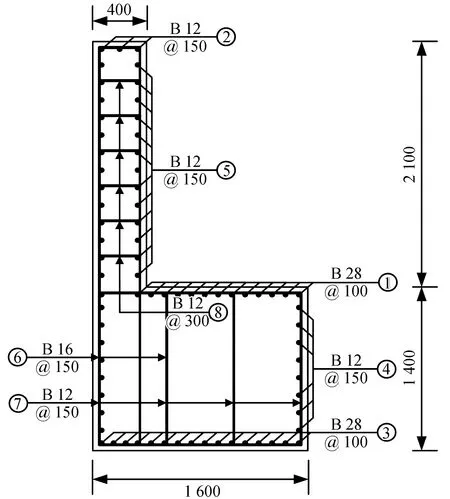
注:⑥背墙箍筋⑦台帽水平拉筋图2 桥台钢筋布置(单位:mm)Fig.2 Abutment steel layout (Unit:mm)

2 有限元模型

本文采用ABAQUS软件对座式桥台进行有限元建模分析,钢筋均采用两结点线性三维桁架单元(T3D2),混凝土和回填土采用八结点线性六面体减缩积分单元(C3D8R)。钢筋本构关系为理想双线性模型,混凝土应用塑性损伤模型,塑性参数指标分别设置为膨胀角30°,偏心率0.1,fb0/fc0为1.16,K为0.667,黏聚系数为0.005。钢筋及混凝土的其他材料参数按照《混凝土结构设计规范》[12]中相关规定选取,如表1所列。回填土选用莫尔-库仑模型,其参数采用Bozorgzadeh的回填土试验数据[13],满足CALTRANS抗震设计标准[10],详情列于表2。

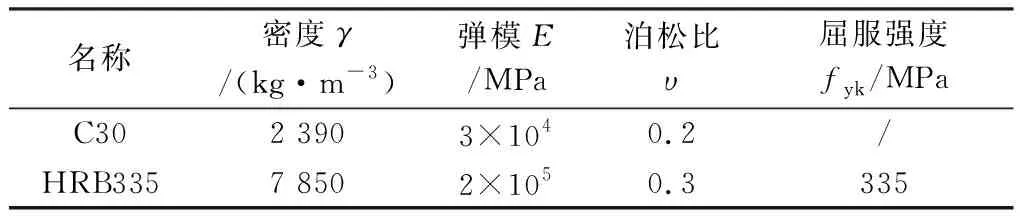
表1 混凝土及钢筋参数

表2 回填土参数

桥台由背墙、耳墙、台帽和基础四部分组成,桥台基础和台帽的强度和刚度较大,地震作用下一般不会发生破坏且变形很小[14],强度较低的耳墙对桥台—主梁纵桥向作用下贡献小[13],因此本文将桥台按照图3简化处理。

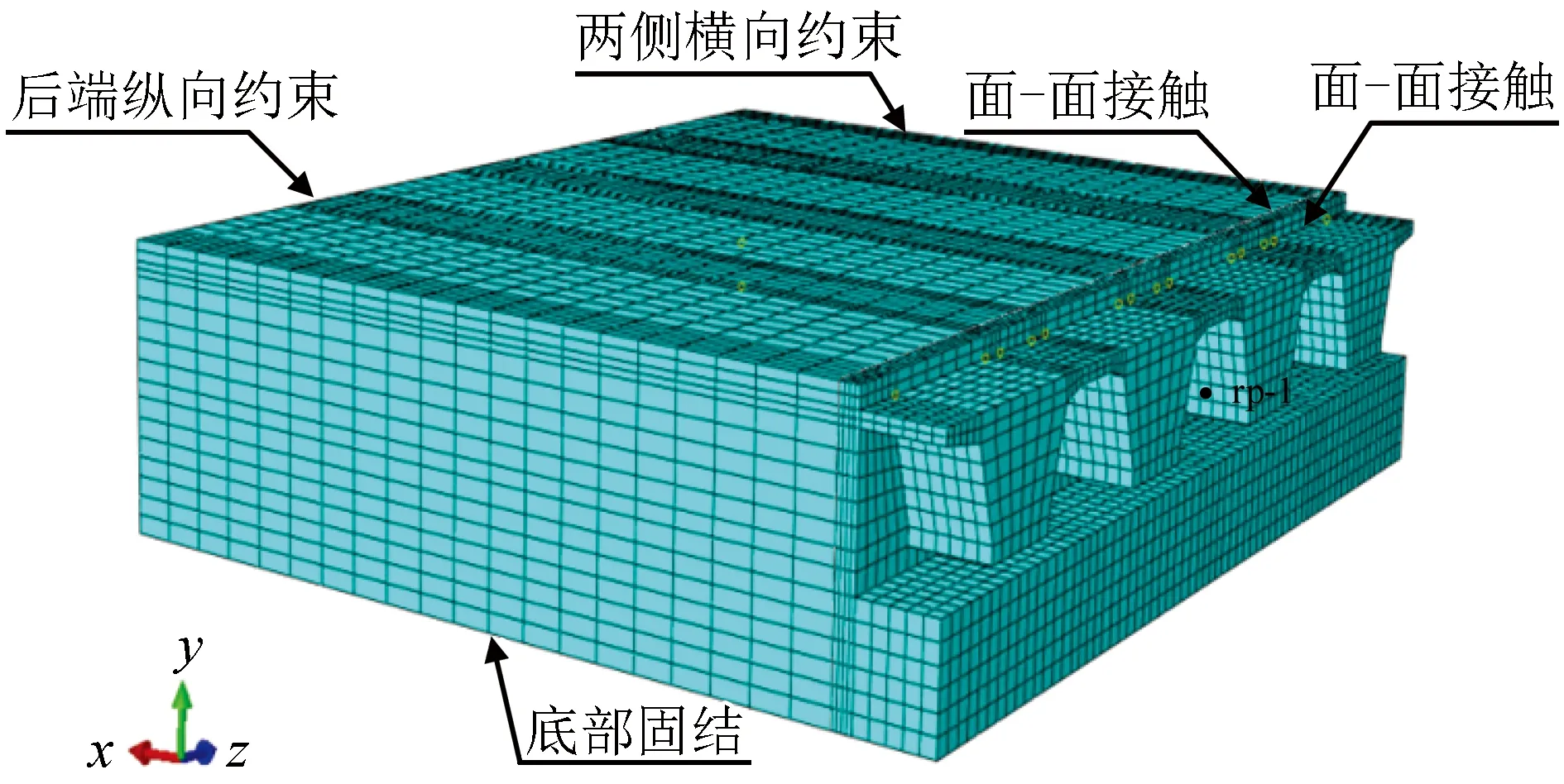
图3 有限元模型Fig.3 Finite element model

为了真实反映桥台构造参数对其抗震性能的影响,建立全尺寸有限元模型,约束条件为桥台底部和台后填土底部施加全部约束,台后填土后端约束纵桥向位移,模型两侧约束横桥向变形,回填土与背墙间、主梁与背墙间均采用面-面接触模拟上部结构-桥台-土体的相互作用。

采用pushover分析方法研究桥台抗震性能,对主梁表面形心rp-1进行位移控制,沿纵桥向缓慢加载,直至峰值荷载下降10%为止[15]。

3 正交数值试验设计

桥台构造参数对桥台抗震性能的敏感性分析体系为多因素共同作用的体系,本文选用正交试验设计法,对该体系进行多因素敏感性分析。根据该桥台原有的设计参数,并结合刘洋[11]及后续40座中小跨径桥梁座式桥台的统计数据,发现各钢筋直径基本不变,间距波动较大。本文借鉴Megally等[16]的研究成果,选取背墙箍筋间距(Sw)、台帽水平拉筋间距(Sa)、背墙厚度(b)以及主梁作用高度(主梁底部到台帽顶面的距离h)作为正交试验的影响因素进行参数分析。将每个影响因素分为3个水平,选用L9(34)正交表,需进行9次数值分析试验,各因素水平及正交数值模拟试验方案分别列于表3、表4。

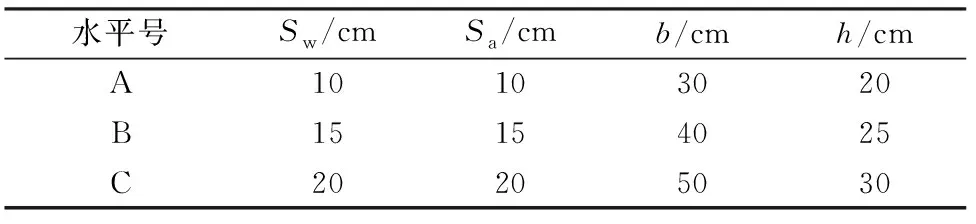
表3 因素水平表

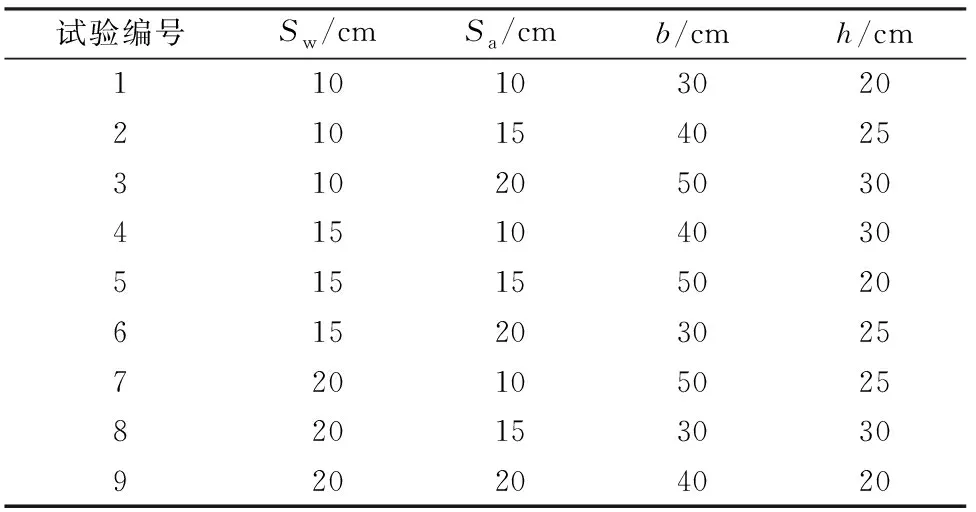
表4 正交数值模拟试验方案

4 参数敏感性分析

各个数值试验下主梁rp-1的力-位移骨架曲线如图4所示。为了能反映各构造设计参数变化对桥台抗震性能的影响程度,本文选取峰值位移、峰值荷载、平均刚度、位移延性系数4个指标为目标函数,以极差分析结果来表示桥台构造设计参数变化对各目标函数的敏感性。峰值荷载是桥台进行pushover静力分析过程中,所达到的最大荷载fult;峰值位移为峰值荷载所对应的位移ymax;平均刚度是过原点及50%峰值荷载点的割线刚度K50[17];位移延性系数为峰值位移ymax与50%峰值荷载点对应的位移y50的比值u,详细情况见图4。

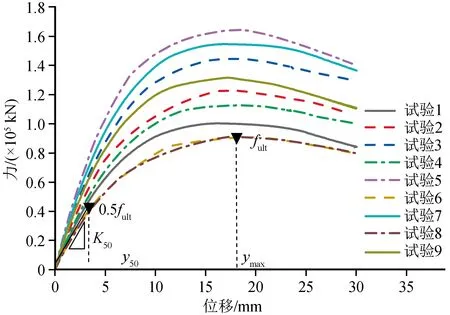
图4 各个数值试验下桥台的力-位移骨架曲线Fig.4 Force-displacement skeleton curves of abutment under various numerical tests

4.1 峰值位移影响

对峰值位移进行影响因素敏感性分析,表5为峰值位移各影响因素分析结果,图5为各因素敏感度数值对比图,图6为峰值位移与各影响因素的关系。

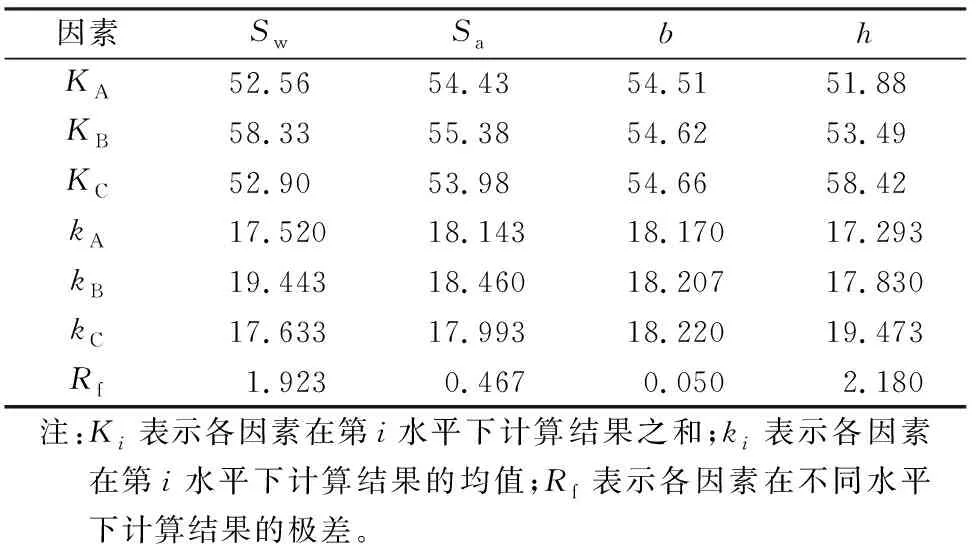
表5 峰值位移影响因素分析结果(单位:mm)

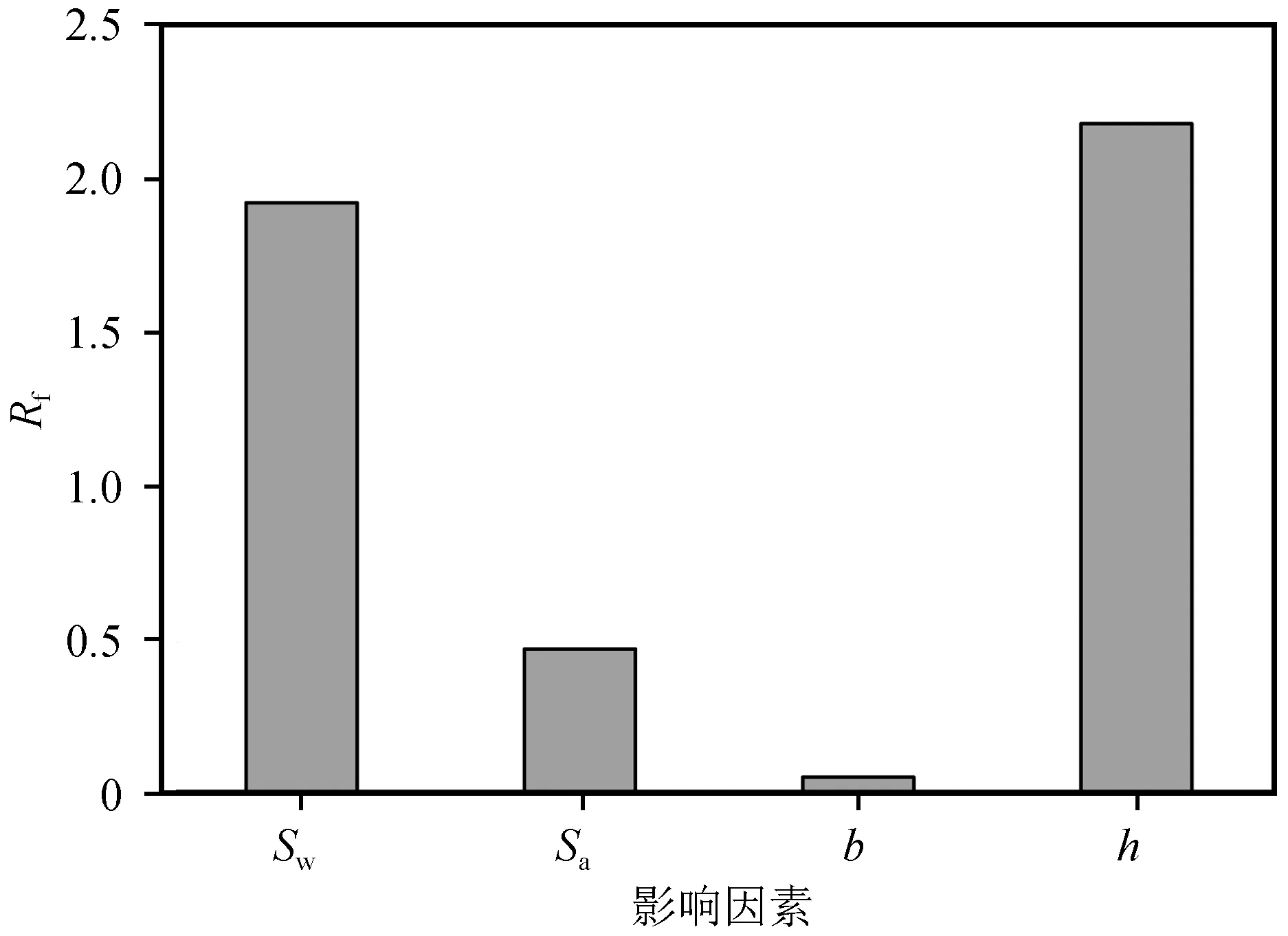
图5 峰值位移影响因素敏感度对比Fig.5 Sensitivity comparison of influencing factors of peak displacement

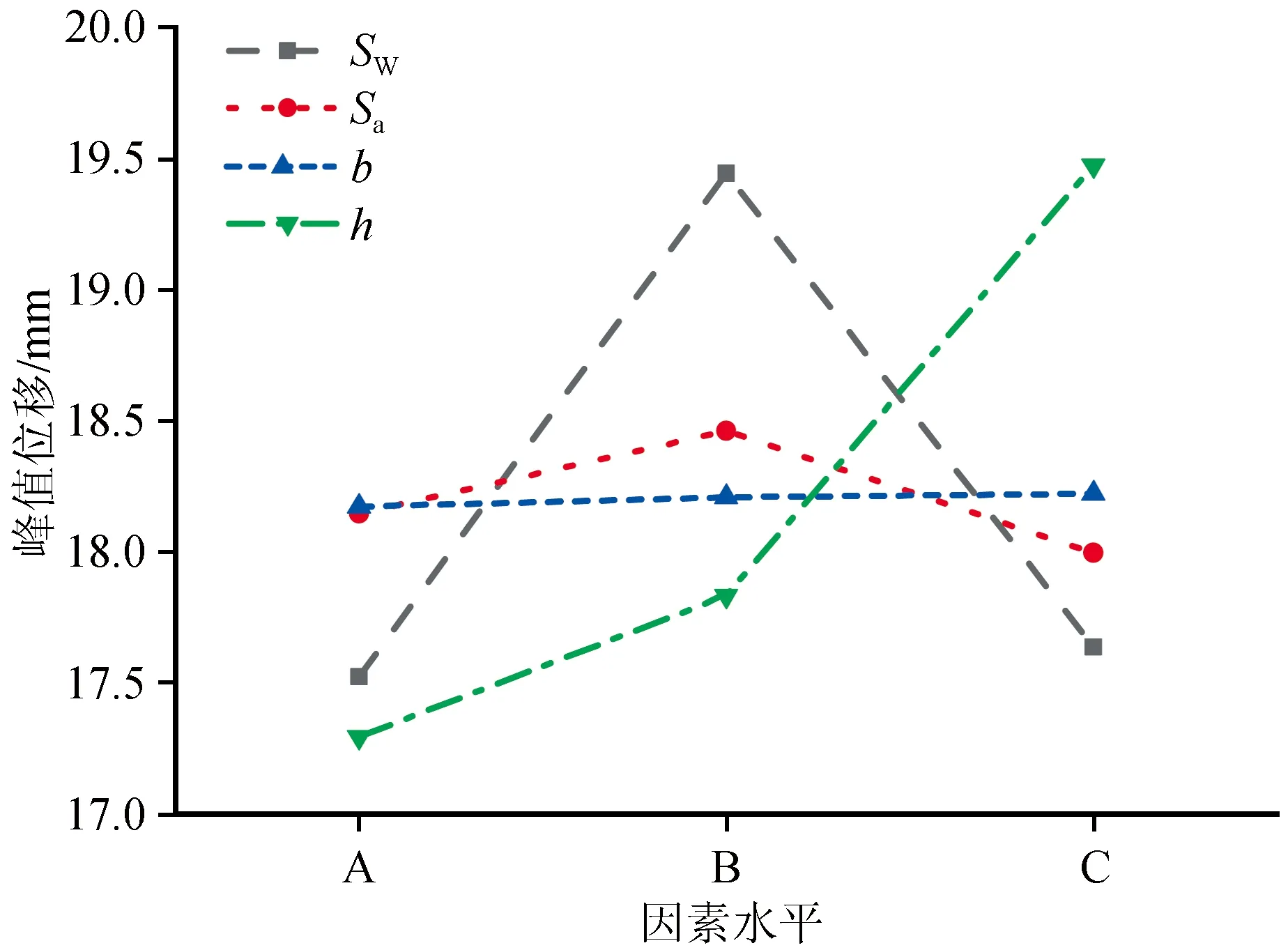
图6 峰值位移与影响因素的关系Fig.6 Relationship between the peak displacement and the influencing factors

根据峰值位移影响因素敏感性分析结果,主梁作用高度对桥台峰值位移影响最大,随着主梁作用高度的增大,峰值位移呈递增趋势,最大增加了9.2%;其次是背墙箍筋间距和台帽水平拉筋间距,由于多影响因素耦合,随着间距增大,峰值位移均呈先递增后递减的趋势,背墙箍筋间距增大使峰值位移变化值最大不超过11%,台帽水平拉筋间距增大使峰值位移变化值不超过2.6%;背墙厚度影响最小,峰值位移在数值上相差不大,不超过0.3%。

4.2 峰值荷载影响

对峰值荷载进行影响因素敏感性分析,表6为峰值荷载各影响因素分析结果,图7为各因素敏感度数值对比图,图8为峰值荷载与各影响因素的关系。

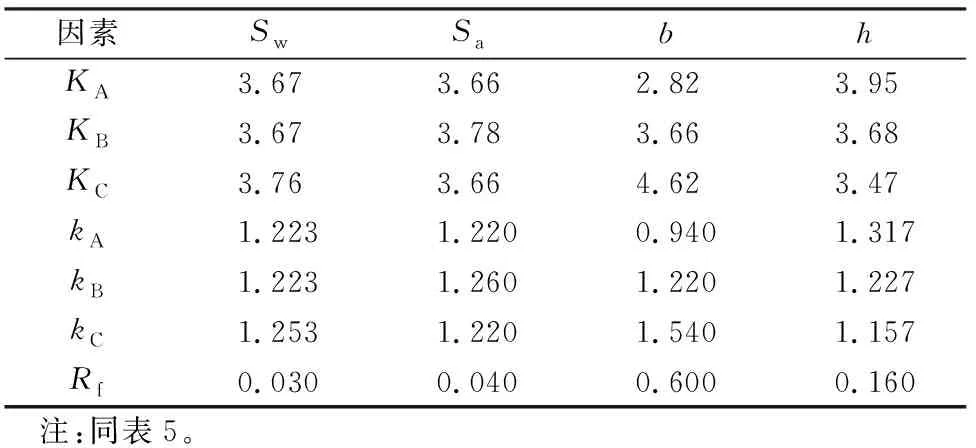
表6 峰值荷载影响因素分析结果 (×105 kN)Table 6 Analysis results of the factors affecting thepeak load (×105 kN)

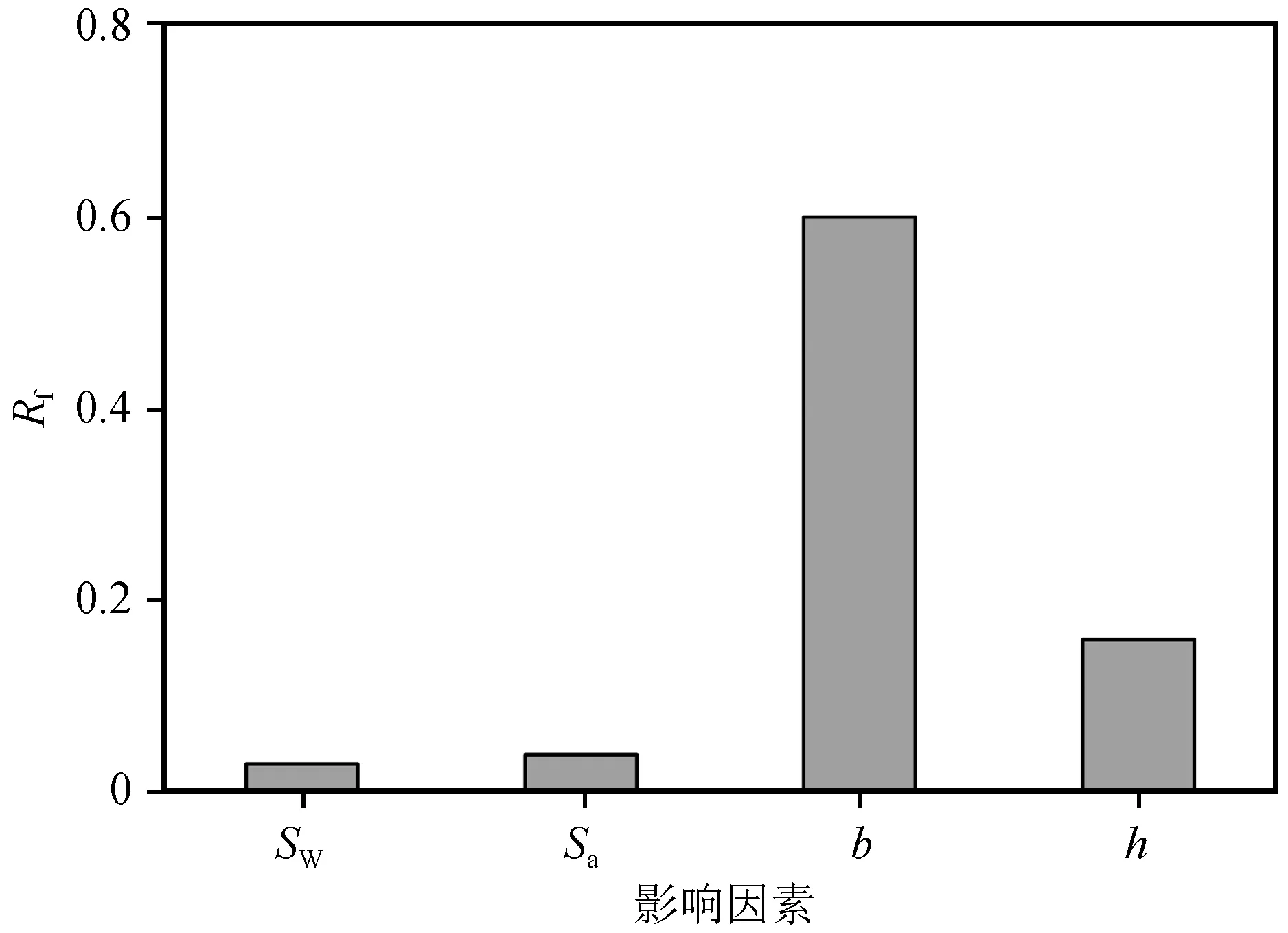
图7 峰值荷载影响因素敏感度对比Fig.7 Sensitivity comparison of influencing factors of peak load

根据峰值荷载影响因素敏感性分析结果,背墙厚度对桥台峰值荷载影响最大,随着背墙厚度的增大,峰值荷载呈递增趋势,最大增加了29.8%;其次是主梁作用高度,随着主梁作用高度增大,峰值位移呈递减的趋势,最大减小了6.8%;由于多影响因素耦合,随着台帽水平拉筋间距增大,峰值荷载呈先增大后减小趋势,数值上相差不超过3.3%;背墙箍筋间距对峰值荷载影响最小,峰值荷载变化不超过2.5%。

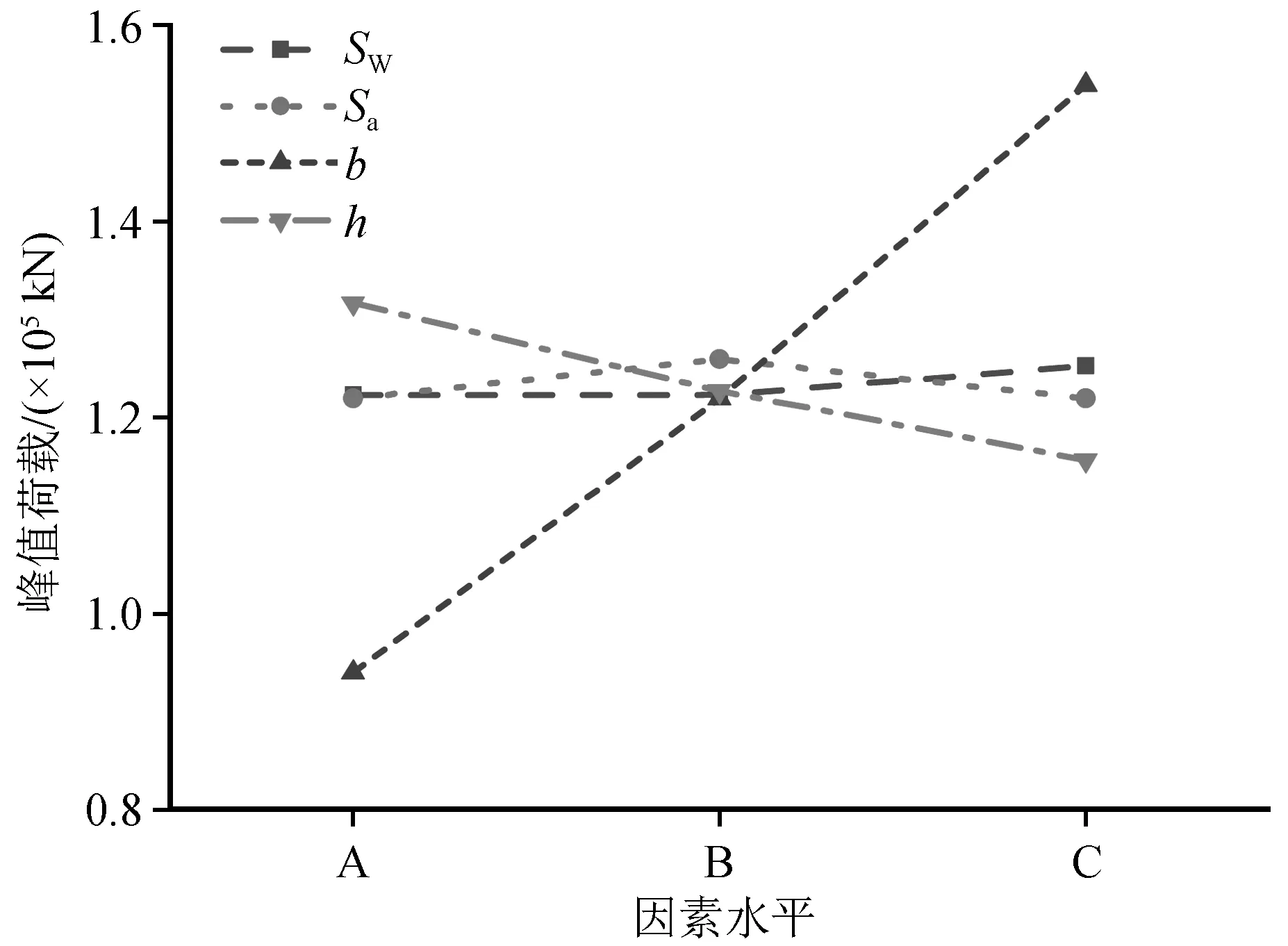
图8 峰值荷载与影响因素的关系Fig.8 Relationship between the peak load and the influencing factors

4.3 平均刚度影响

对平均刚度进行影响因素敏感性分析,表7为平均刚度各影响因素分析结果,图9为各因素敏感度数值对比图,图10为平均刚度与各影响因素的关系。

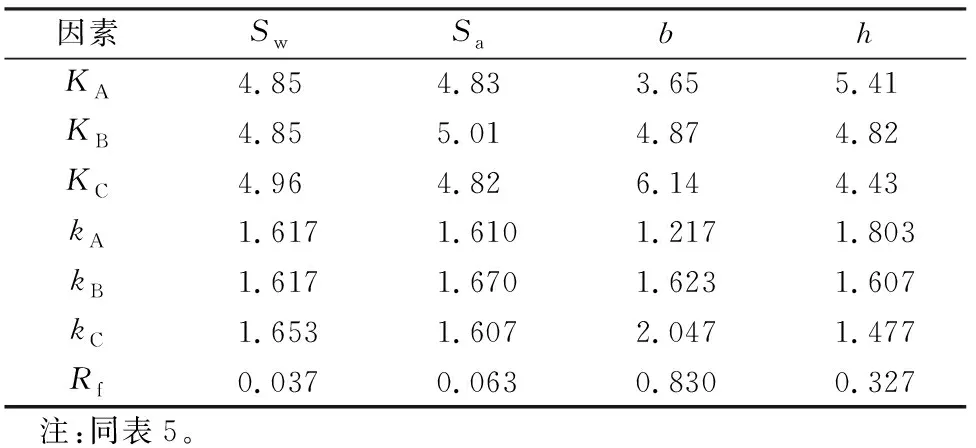
表7 平均刚度响因素分析结果 (×104 kN/mm)Table 7 Analysis results of the factors affecting the average stiffness (×104 kN/mm)

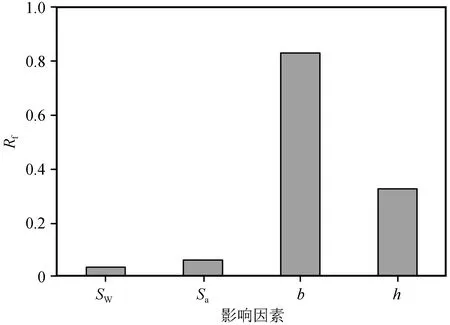
图9 平均刚度影响因素敏感度对比Fig.10 Sensitivity comparison of influencing factors of average stiffness

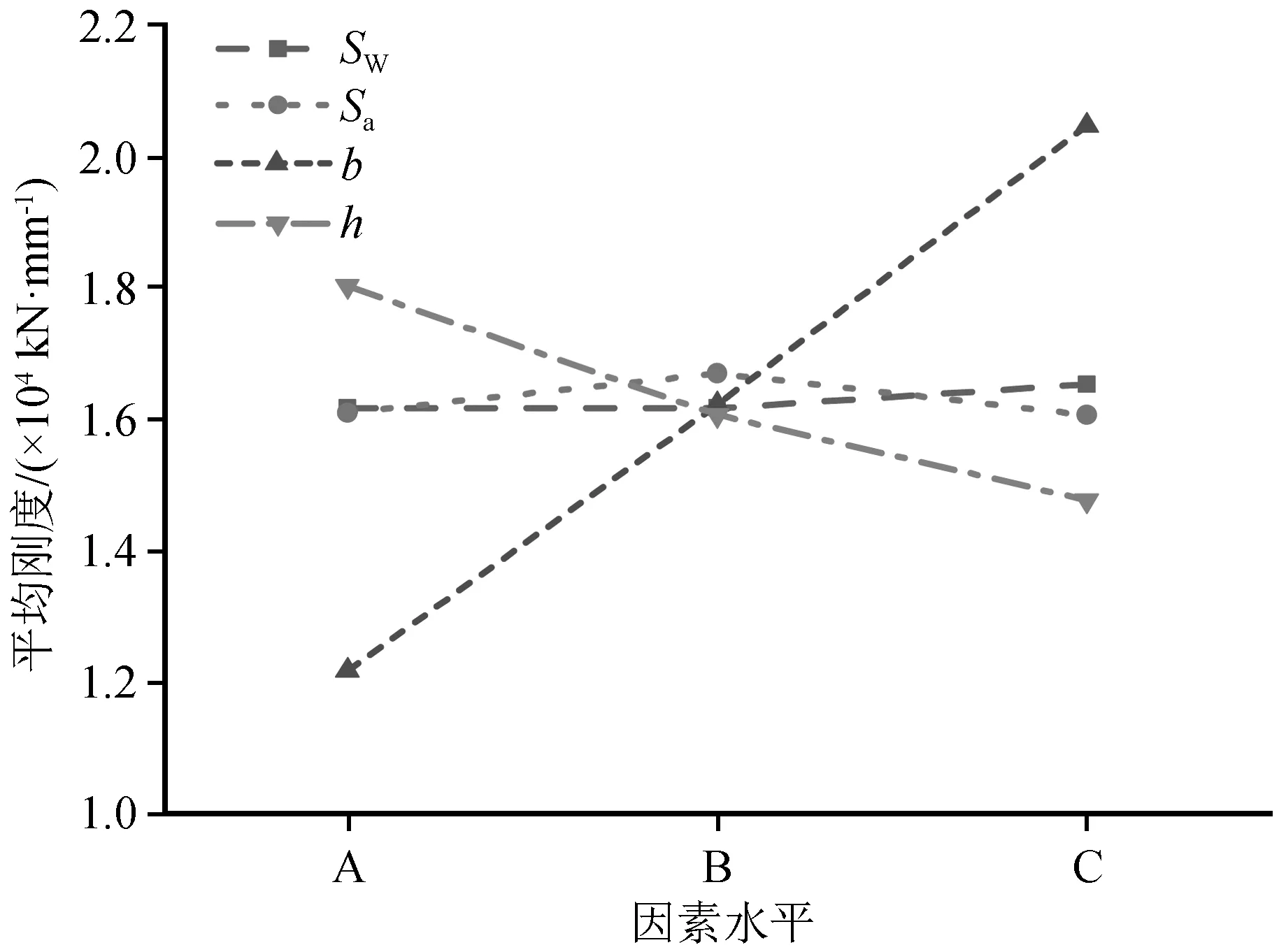
图10 平均刚度与影响因素的关系Fig.10 Relationship between the average stiffness and the influencing factors

根据平均刚度影响因素敏感性分析结果,背墙厚度对桥台平均刚度影响最大,随着背墙厚度的增大,平均刚度呈递增趋势,最大增加了33.36%;其次是主梁作用高度,随着主梁作用高度增大,平均刚度呈递减的趋势,最大减小了10.9%;由于多影响因素耦合,随着台帽拉筋间距增大,平均刚度呈先递增后递减的趋势,数值上相差不超过3.8%;背墙箍筋间距对平均刚度影响最小,平均刚度变化不超过2.3%。

4.4 位移延性系数影响

对位移延性系数进行影响因素敏感性分析,表8为位移延性系数各影响因素分析结果,图11为各因素敏感度数值对比图,图12为位移延性系数与各影响因素的关系。

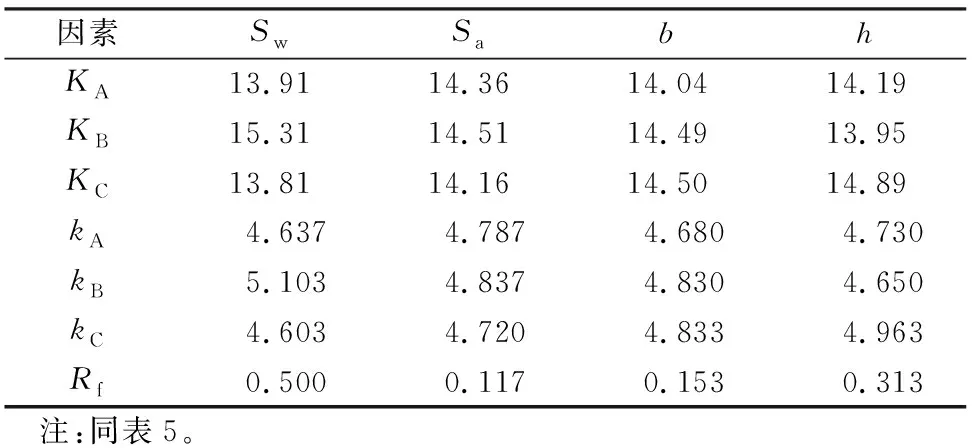
表8 位移延性系数影响因素分析结果

根据位移延性系数影响因素敏感性分析结果,背墙箍筋间距对桥台位移延性系数影响最大,其次是主梁作用高度。由于多种影响因素耦合,背墙箍筋间距和主梁作用高度的变化使桥台位移延性系数均呈现不单调趋势。随着箍筋间距的增大,位移延性系数呈先递增后递减的趋势,变化幅度不超过10%;随着主梁作用高度增大,位移延性系数呈先递增后递减的趋势,最大变化幅度为6.7%;随着背墙厚度增大,位移延性系数呈递增趋势,数值上相差不超过3.2%;台帽水平拉筋间距对位移延性系数影响最小,位移延性系数变化不超过2.5%。

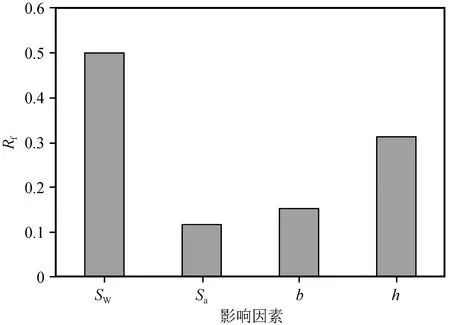
图11 位移延性系数影响因素敏感度对比Fig.11 Sensitivity comparison of influencing factors of displacement ductility coefficient

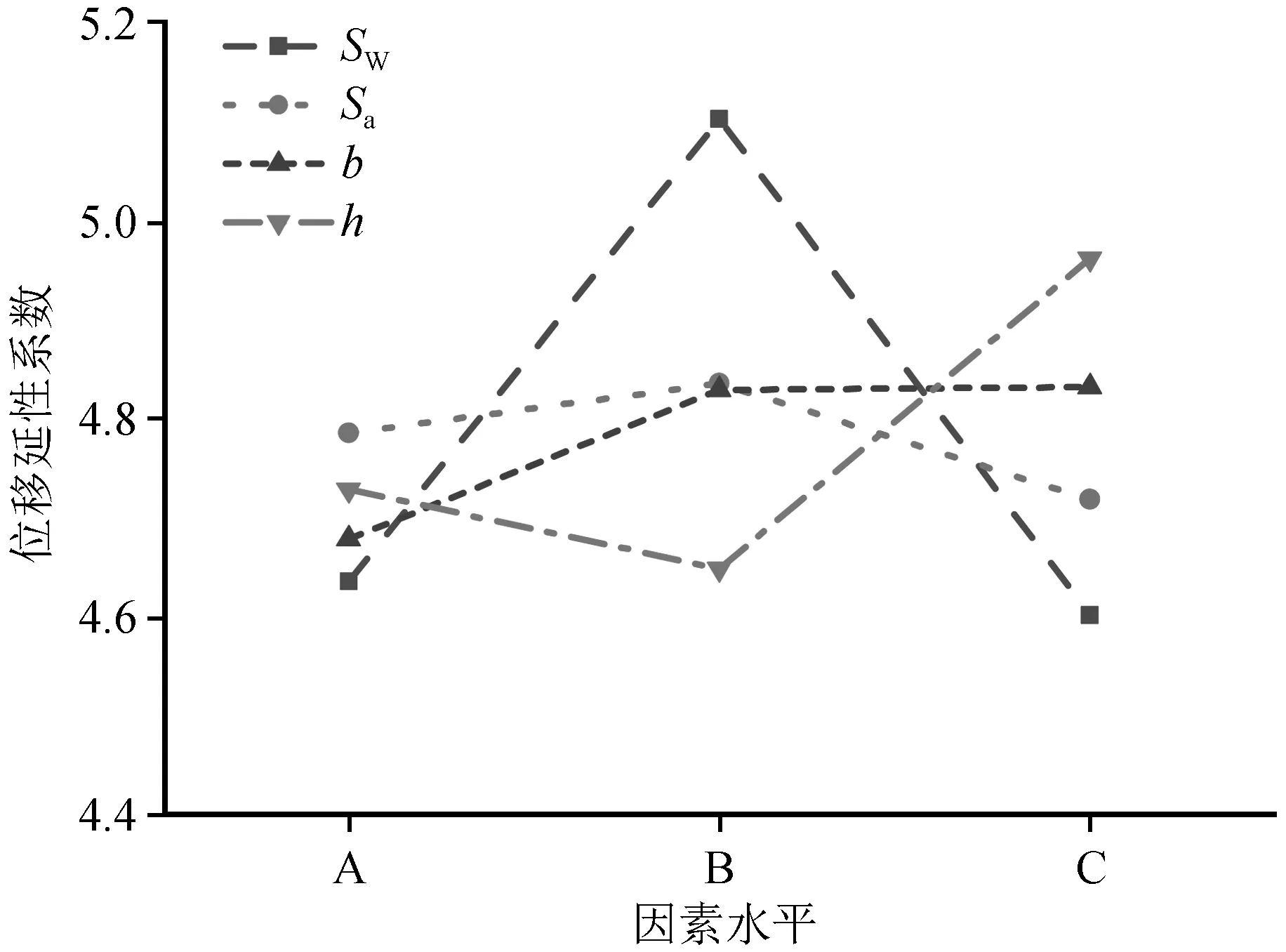
图12 位移延性系数与影响因素的关系Fig.12 Relationship between the displacement ductility ratio and the influencing factors

5 结论

本文基于某座3×30 m跨径桥桥台,并结合40多座中小跨径的座式桥台构造设计参数统计结果,建立座式桥台简化模型,进行pushover分析,采用正交数值试验方法研究了桥台上部结构参数变化对桥台抗震性能指标的影响规律及敏感性,得到以下结论:

(1) 对桥台峰值荷载和平均刚度影响最大、最敏感的构造参数是背墙厚度。随着背墙厚度的增加,峰值荷载和平均刚度最大分别增大29.8%和33.4%,适当增加背墙厚度对于桥台刚度的提高有着重要意义;

(2) 主梁作用高度和背墙箍筋间距对桥台峰值位移及位移延性有着较大影响。主梁作用高度的增大使桥台峰值位移最大增加9.2%,背墙箍筋间距的增大使峰值位移变化幅度不超过11%。主梁作用高度和背墙箍筋间距的增大使桥台位移延性系数变化幅度分别不超过10%和6.7%,可以结合桥台刚度的实际需求,适当增大主梁作用高度及背墙箍筋间距,提高桥台延性;

(3) 本论文在对桥台抗震性能进行参数敏感性分析时,采用pushover分析方法对桥台进行建模分析,尚未进行考虑主梁撞击的动力分析。随着此课题的深入研究,这些工作会进一步展开。