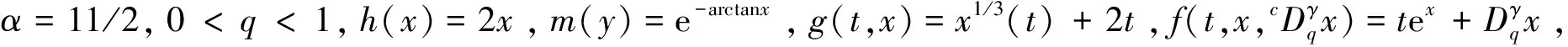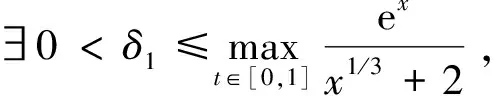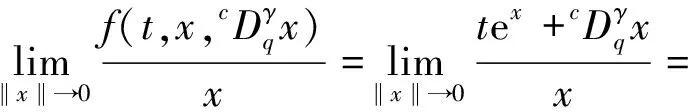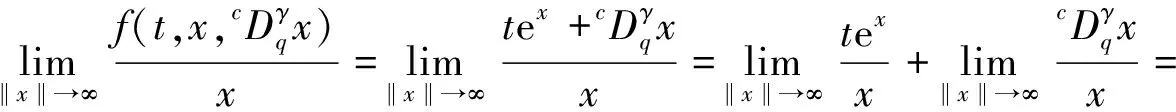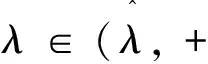关于分数阶q-差分方程正解的存在性
田春平 顾海波 孙会贤
(新疆师范大学数学科学学院,830017,乌鲁木齐)
1 引 言
分数阶微积分相对来说,能更加精确地描述实际问题,提供更丰富的信息.近年来,国内外分数阶差分边值问题的研究也非常的活跃[1-8].2015年, Li等人[9]通过不动点定理,研究了基于不含时的、定态的分数阶q-差分薛定谔方程边值问题:
(1)
并得到了方程解的存在性结果.对于分数阶q-差分方程边值问题的正解[10-15]也有许多学者作了探究.2019年,Mao等人使用迭代法研究了如下方程解的唯一性,其中非线性项含有两个空间变量,且对第二个空间变量可以是奇异的:
(2)
之后Liu等人[16]研究了一类带有扰动项的问题:
并利用混合单调算子不动点定理证明了该问题解的存在唯一性,构造出了两个迭代序列的逼近解.
基于以上讨论,本文主要研究如下方程在参数λ的影响下边值问题的解的存在性结果:
(3)

文章内容分为四个部分.在第二节中,给出了相关定义、性质和引理.第三节是本文主要结论,首先借助格林函数讨论了退化方程解的情况,以及在参数影响下解的存在性结果,然后给出具体实例进行说明.
2 预备知识
为便于定理证明的需要,下面给出一些定义、符号和引理.
记⎣α」是小于或等于α的最大整数,「α⎤是大于或等于α的最小整数.
定义1[4]在复数域C中,q-差分阶乘为
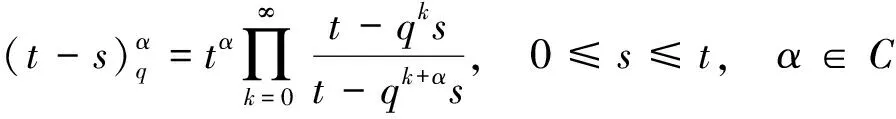
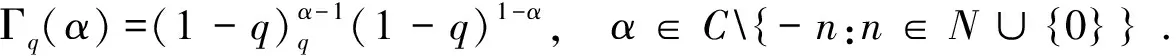
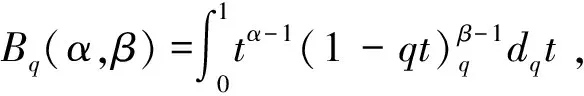
定义4[4]设f(t)是定义在q-几何集Tq中的实值函数,|q|<1,f(t)的q-微分定义为
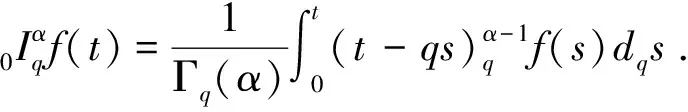
定义6[1]令α>0,n=「α⎤,则f(t)的Caputo型的q-α型分数阶微分定义如下:
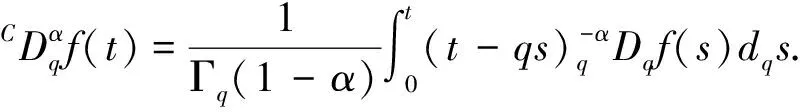

引理1[16]令p(t)∈C[0,1],方程
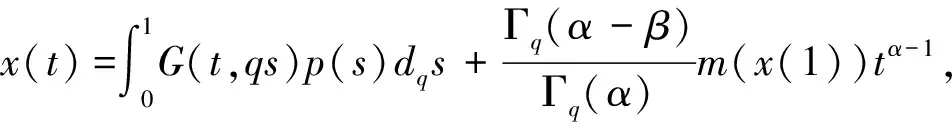
(4)
引理2[11,16]格林函数具有以下性质:
1)G(t,qs)≥0且G(t,qs)≤G(1,qs),∀0≤t,s≤1;
2)G(t,qs)≥tα-1G(1,qs),∀0≤t,s≤1;
4)0≤tα-1qα-β(1-qs)α-β-1≤Γq(α)G(t,qs)≤tα-1(1-qs)α-β-1;
证性质1),2)见文献[11], 性质4),5)见文献[16].下面证明性质3)成立.
≥1,
(1-qs)(α-β-1)-(1-qs)(α-1)
=(1-qs)·(1-q2s)·…·(1-qα-β-1s)-(1-qs)·(1-q2s)·…·(1-qα-1s)
=(1-qs)·(1-q2s)·…·(1-qα-β-1s)(1-(1-qα-βs)·(1-qα-β+1s)·…·(1-qα-1s)
<1,
引理3Gamma函数的性质:
1)Γq(α)>Γq(α-γ)>Γq(α-β)>1;
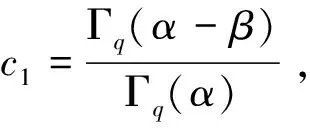

证性质1)、2)、3)同引理2性质3)证明类似, 在此不再验证.
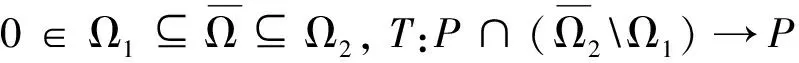
1)对于x∈P∩∂Ω1,‖Tx‖≤‖x‖,并且对于x∈P∩∂Ω2,‖Tx‖≥‖x‖(即锥拉伸),
或
2)对于x∈P∩∂Ω1,‖Tx‖≥‖x‖,并且对于x∈P∩∂Ω2,‖Tx‖≤‖x‖(即锥压缩),
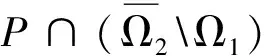
在本文中,做如下假设:
当固定t∈[0, 1]关于x是不减的,且存在常数σ∈(0,1),∀r∈(0,1]有g(t,rx)≥rσg(t,x),其中x∈[0,+∞);
(H2)g(t,0)在t∈[0,1]上不恒为0,且存在常数δ1>0,对任意t∈[0,1],使得f(t,x,y)≥δ1g(t,x),x,y∈[0,+∞);
(H3)m(x)关于x∈[0,∞)递减,且存在δ2>0,使0 注1其中(H1)蕴含着:∀r>1,有g(t,rx)≤rσg(t,x). 本节中将讨论分数阶方程在参数影响下正解的存在性. 由引理1可知方程(3)等价于下面的积分形式: (5) 其中G(t,qs)由(4)式给出. 当λ=0时,方程(3)退化为方程: (6) P1={x∈E0|∃常数0 定理1假设条件(H1)成立,那么方程(6)至少有一个正解x*∈P1,并且存在一个常数0 证(Ⅰ)首先断言T:P1→P1是不减的. ≥kTxtα-1, ≤(kTx)-1tα-1, 其中kTx是一个正常数,且满足: 和 因此,存在常数0 x0=δa(t) ,xn=T(xn-1),n=1,2,3…, y0=δ-1a(t) ,yn=T(xn-1),n=1,2,3…, 则有x0≤x1≤…≤xn≤…≤yn≤yn-1≤…≤y1≤y0,且∃x*∈P1,使xn(t)→x*(t)在[0,1]上一致成立. 事实上,0<δ<1,x0,y0∈P1且x0 x1=Tx0(t) ≥δσTa≥δσkTaa(t)≥δσ·δ1-σa(t)=x0, 所以有x0≤x1≤…≤xn≤…≤yn≤yn-1≤…≤y1≤y0. 令c0=δ2, 0 xn=T(xn-1)=Tn(x0)=Tn(δa(t))=Tn(c0δ-1a(t))≥c0σnTn(δ-1a(t))=c0σnTn(y0)=c0σnyn, 所以存在一个x*∈P1,使得xn(t)→x*(t)在[0,1]上一致成立,即(Ⅱ)成立.综上所述,T为连续算子,xn=Txn-1,令n→∞,有x*=Tx*是方程(3)的正解,因为∃x*∈P1,所以存在0 当λ>0时,在Banach空间E中,存在常数0<τ<1,定义 定义算子Tλ:P2→E,满足下述条件: 定理2假设条件(H1)-(H4)成立,则映射Tλ是全连续的. 证(Ⅰ)首先易知Tλ:P2→E是连续算子.其次∀x∈P2,由引理2得 =τα-1‖Tλx‖, 所以Tλ(P2)⊂P2. (Ⅱ)任取P2中一个有界子集Ω,Ω⊂P2,那么对∀x∈Ω,∃M>0使‖x‖≤M. 因为 所以‖Tλx‖E<∞,Tλ(Ω)是一致有界的. 其中 故 |Tλx(t2)-Tλx(t1)| 当t1→t2). 又 而 所以当t1→t2时, ‖Tλx(t2)-Tλx(t1)‖E→0,在空间E中Tλx是等度连续的.故由Ascoli-Arzela定理可得,Tλ:P→P是全连续算子.证毕. 记 则方程(3)至少存在一个正解x*,且min{u,v}≤‖x*‖≤max{u,v}. 证令Ωu={x∈E:‖x‖ 所以 也就是说,当x∈∂Ωu,有‖Tλx‖≤‖x‖.令 Ωv={x∈E:‖x‖≤v},∀x∈∂Ωv,τv<‖x‖ Tλx(t) 因此对x∈∂Ωv,有‖Tλx‖≥‖x‖. 定理4假设(H1)-(H4)成立,且(H5),(H6)其中一个成立,且 则对∀0<λ<λ*,方程(3)至少有一个正解. q:(0,∞)→(0,∞)是连续的.那么对于0<λ<λ*,∃0 易知 另外由假设(H5)与(H6)可知,∃v1,v2,0 因此 推论1若假设(H1)-(H6)成立, 那么对∀0<λ<λ*方程(3)至少存在两个正解. 定理5假设(H1)-(H4)成立,(H7),(H8)其中一个成立,且 下面将给出两个具体算例检验本文的研究结果. 例1考虑下面边值问题: (7) 显然∀r∈(0,1],∃σ=1/2,有g(t,rx)≥rσg(t,x), ∃δ2=1,使0≤m(y)≤1, 因此,假设(H1)-(H4),(H5)-(H6)成立,那么由推论1,边值问题(7)对任意λ∈(0,λ*)至少有两个正解存在. 例2考虑边值问题: (8) 显然∀r∈(0,1], ∃σ=1/2, 有g(t,rx)≥rσg(t,x), ∃δ2=1,使0≤m(y)≤1,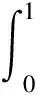
3 主要结果

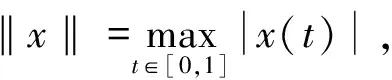
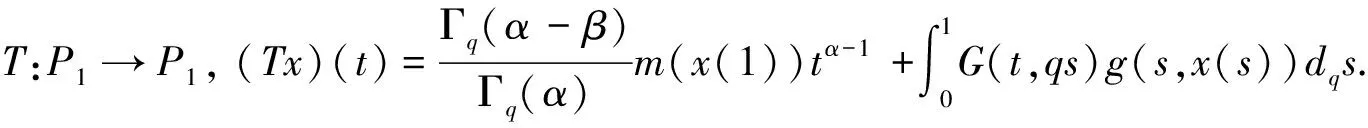
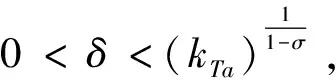

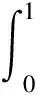
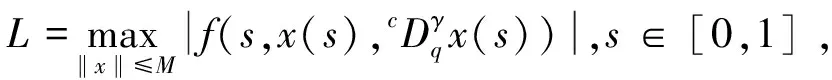
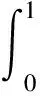
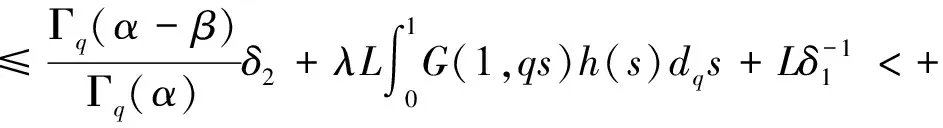
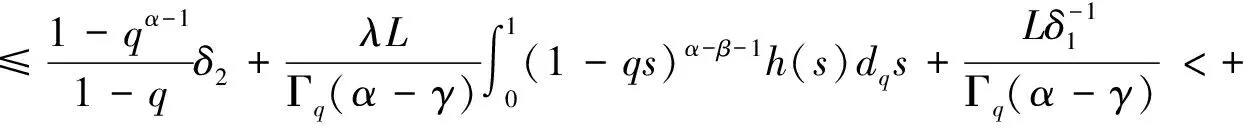
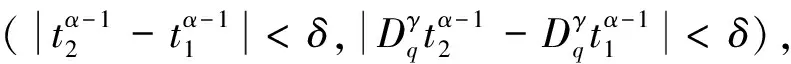
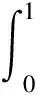

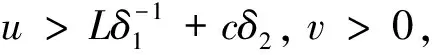
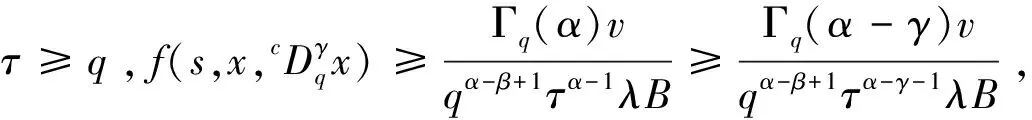

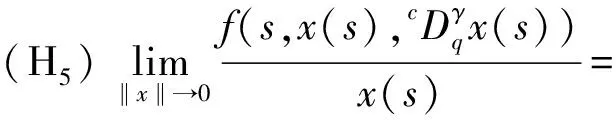
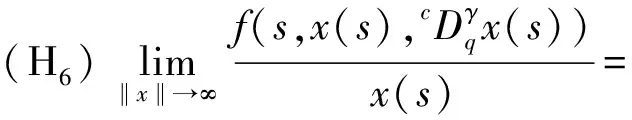
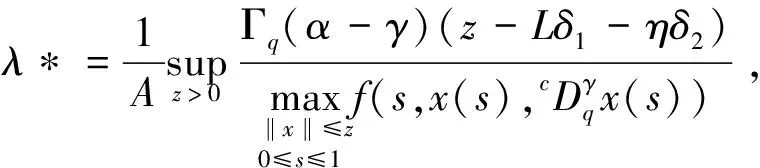

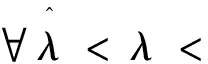
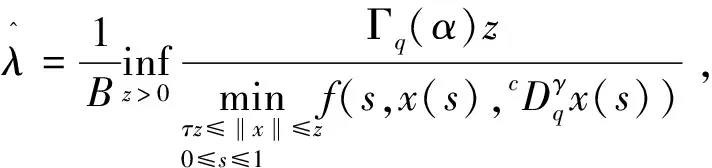

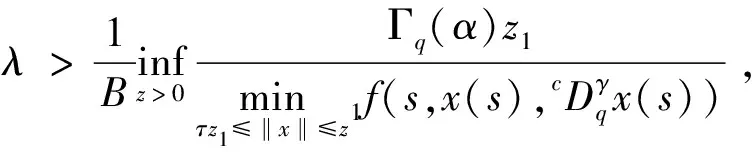

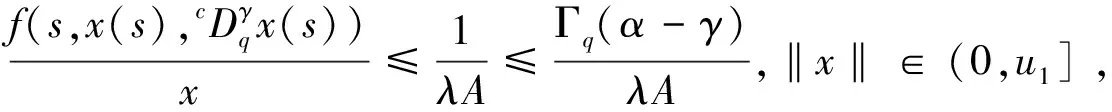

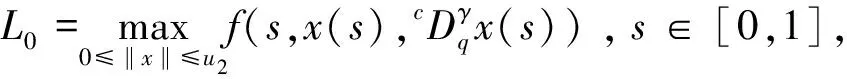
4 算 例