分数阶方程约束最优控制问题数值算法研究进展

周兆杰 王方圆 王起明 刘 杰

(山东师范大学数学与统计学院，250358，济南)

1 引 言

微分方程最优控制问题通常包含需要优化的目标泛函、控制变量和状态变量，其中控制变量和状态变量通过微分方程的形式耦合，通常称该微分方程为状态方程.根据对控制变量或状态变量施加的约束不同，微分方程最优控制问题可分为无约束问题、控制约束问题和状态约束问题.在过去的几十年中，关于整数阶微分方程最优控制问题的研究取得了很大的发展，已有许多知名学者在控制理论及数值算法方面做了大量的研究工作[1-7].

近年来，随着分数阶微积分理论及应用的快速发展，关于分数阶方程约束最优控制问题的研究引起了学者们的广泛关注.分数阶方程约束最优控制问题在工程领域中有着广泛的应用，例如，地下水的污染控制问题.该问题的目标在于使得地下水中污染物浓度在给定的区域中保持在一个可容许范围之内，同时又使得所付出的代价最小，其数学模型可表示为状态逐点约束的分数阶最优控制问题，其中状态变量代表污染物浓度，并并满足分数阶对流扩散方程.

与整数阶问题相比，分数阶导数的非局部性导致状态方程的解在时间区间端点或空间区域边界处具有奇性，即使已知数据是光滑的，也会使得带约束的分数阶最优控制问题解的光滑性要比整数阶控制问题解的光滑性差.此外，带约束的最优控制问题在数值离散后所得的代数系统是一个由离散状态方程、伴随方程及离散最优不等式耦合在一起的非线性系统，通常需要进行迭代求解.而分数阶导数的非局部性通常会导致离散后状态方程和伴随方程的系数矩阵不稀疏，这就使得用数值迭代方法求解上述代数系统时的耗费比整数阶最优控制问题大得多.这些问题给分数阶最优控制问题的数值求解和数值分析带来了很大困难.

随着分数阶微积分理论及数值计算方法的快速发展，关于分数阶最优控制问题理论及数值算法的研究成为国内外研究者广泛关注的一个热点问题.因此，本文将对近年来关于分数阶微分方程约束最优控制问题数值算法方面的研究工作进行梳理概述，并在此基础上进行研究展望，以期为分数阶方程约束最优控制问题的深入研究提供参考.

2 基础知识

分数阶微积分具有悠久的发展历史，众多数学家对这一领域进行了研究，提出了多种分数阶积分和导数的定义.近年来，分数阶微积分在物理、工程等领域中的应用日益广泛，这大大激发了学者们对分数阶微积分理论的研究兴趣.

2.1分数阶积分常用的分数阶积分定义主要有以下两种：

和

其中，ν∈L1(a,b)，0<μ<1，x∈[a,b],这里Γ(·)为Gamma函数.

2.2分数阶导数常用的分数阶导数定义有Rieman-Liouville型、Caputo型和分数阶拉普拉斯算子.

1)Rieman-Liouville型.Rieman-Liouville型左分数阶导数和右分数阶导数定义如下：

2)Caputo型.为了更好的完成工程与物理的建模，20世纪60年代意大利物理学家Caputo提出弱奇异的Caputo分数阶导数的定义，有效地解决了Rieman-Liouville型分数阶导数中的初值问题.Caputo型左分数阶导数和右分数阶导数定义如下：

3)分数阶拉普拉斯算子.常见的分数阶拉普拉斯算子的定义方式主要包括谱定义和积分定义两种.

① 谱定义的分数阶拉普拉斯算子为

其中，1<α<2，λk和ek分别为(-Δ)在Dirichlet或Neumann边界条件下的特征值和特征函数.

② 积分型分数阶拉普拉斯算子定义为

其中，1<α<2，常数C(d,α)定义为

“P.V.”表示积分的主值，定义为

Bε(x)是一个以x为心半径为ε的球.

2.3分数阶最优控制问题

2.3.1 时间分数阶最优控制问题 控制受限的时间分数阶最优控制问题可表示为

(1)

且满足下述条件：

(2)

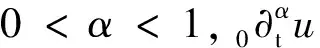
控制集的定义如下：

Uad={q∈L2(ΩT):a≤q(x,t)≤b,a,b∈R且a≤b}.

状态方程(2)还可以写为

故时间分数阶最优控制问题还有如下形式：

且满足下述条件：

上述模型中状态方程的初值可以不为0.

2.3.2 空间分数阶最优控制问题

1)一维问题.设Ω=(0，1)，Γ=∂Ω，一维的空间双边分数阶最优控制问题可表示为

且满足下述条件：

其中，常数r∈[0,1]，α∈(1,2).

约束集Uad的定义方式有多种，常见的有如下几种定义：

① 控制约束问题：Uad={q∈L2(Ω):a≤q(x)≤b,a,b∈R且a≤b}，κ=L2(Ω)；

② 逐点状态约束问题：Uad=L2(Ω)，κ={v∈C0(Ω)|v≤b}；

④ 混合约束问题：Uad={q∈L2(Ω):a≤q(x)≤b,a,b∈R且a≤b}，

在上述控制问题中，状态方程也可以带有变扩散系数，如

其中，0

2)二维问题.二维分数阶最优控制问题，常见的是带有分数阶拉普拉斯算子的分数阶最优控制问题，例如：

且满足下述条件：

这里Ω是二维区域，s∈(0,1)，约束集的定义可参考一维情况，分数阶拉普拉斯算子的定义可以是积分型的，也可以是谱定义的.需要指出的是，积分型定义的状态方程的边界条件是非局部的Ωc=R2Ω，而谱定义型状态方程的边界条件为局部的∂Ω.此外，两种定义下，状态方程解的正则性是不一样.

2.3.3 时空分数阶最优控制问题 将时间分数阶与空间分数阶结合，可以得到时空分数阶最优控制问题，例如，设Ω是Rd(d≥1)的有界开区域，∂Ω是边界，目标泛函为

且满足时空分数阶状态方程

其中，分数阶拉普拉斯算子为谱定义型，约束集的定义可参考一维空间分数阶最优控制情况.

2.3.4 其他类型分数阶最优控制问题 上述的最优控制问题都是分布型控制问题，近年来也有学者开始研究一些其他类型的分数阶最优控制问题[8,9].

1)分数阶稀疏控制问题.该问题形式为

且满足下述条件：

其中γ>0,α>0是正则化参数，s∈(0,1)，分数阶拉普拉斯算子为谱定义型.与之前的控制问题相比，这里的目标泛函不再光滑.

2)分数阶抛物Dirichlet外部控制问题.该问题形式为

且满足下述条件:

其中，J(·)是满足弱下半连续的泛函，Uad⊂L2((0,T)，L2(RNΩ))是闭凸集.

3 分数阶最优控制问题的数值算法

对分数阶微分方程约束最优控制问题，在适定性理论方面已有一些研究工作，比如，文献[10]研究了无约束的黎曼-刘维尔型时间分数阶最优控制问题，并分析了控制问题解的存在唯一性，推导了一阶最优性条件.文献[11]研究了状态约束的黎曼-刘维尔型时间分数阶最优控制问题，并分析了控制问题解的存在唯一性，推导了一阶最优性条件.文献[12]研究了带有逐点状态约束的分数阶最优控制问题，并建立了控制问题的适定性，推导了一阶最优性条件.在这些理论结果的基础上，近年来，研究者们发展了一系列求解分数阶偏微分方程约束最优控制问题的数值方法，主要包括有限元法、有限差分法、谱方法、快速算法等.

3.1有限元逼近众所周知，有限元法是求解微分方程的重要工具之一，已有大量的文献运用有限元法求解整数阶最优控制问题和分数阶微分方程.将有限元法应用于求解分数阶最优控制问题的研究工作，近年来受到学者的广泛关注.

3.1.1 时间分数阶最优控制问题 Antil H等人[13]对控制约束的时空分数阶最优控制问题进行了分析和数值逼近，在时间方向上采用L1格式离散，在空间方向上利用Caffarelli-Silvestre延拓将空间分数阶方程转化为半无限圆柱上维数增加一维的非一致椭圆问题，从而避免了直接对空间分数阶导数进行离散，并建立了时间整数阶情况下的先验误差估计，对时间导数为分数阶的情况，证明了离散格式的收敛性.

Zhou Z J等人[14]研究了时间分数阶扩散方程最优控制问题的Galerkin有限元逼近，对状态和伴随状态变量采用分段线性多项式逼近，控制变量采用变分离散，建立了有限元半离散格式的先验误差估计；基于时间分数阶导数的L1离散格式，建立了控制问题的全离散格式，在“先离散后优化”的基础上，推导了全离散一阶最优条件.

Liu Q Y等人[15]提出了一种时间分数阶对流扩散最优控制问题的数值逼近方法.该方法首先用有限元法对空间域进行离散化，然后用控制参数化方法逼近可容许控制，采用隐式有限差分法求解时间分数阶系统，最后得到一个最优参数选择问题.该问题用数值优化算法求解，并用数值结果验证了所提数值逼近方法的有效性和准确性.

Zhou Z J等人[16]将分片常数时间步长间断Galerkin方法与分片线性有限元方法相结合并用于求解控制受限的时间分数阶扩散方程最优控制问题，在先离散后优化方法的基础上，导出了离散一阶最优条件；并针对状态变量和伴随状态变量在时间区间端点处存在弱奇异性的特点，提出了一种基于步长倍频技术的时间自适应算法，用于指导时间网格的细化.

Gunzburger M等人[17]针对时间分数阶偏微分方程约束的最优控制问题提出了一种基于卷积求解时间离散的全离散有限元方法来确定最优系统的近似解，并证明了该方法的最优收敛性，即最优收敛性仅依赖于对数据的正则性假设，而不需要对最优性系统解的正则性进行额外的假设.

Zhang C Y等人[18]对时间分数阶扩散方程最优控制问题的时间步长间断Galerkin有限元逼近进行了先验误差分析，采用时步不连续Galerkin有限元法和变分离散法分别逼近状态变量和控制变量并讨论了最优控制问题的正则性.由于时间分数阶导数是非局部的，为了减少计算量，针对离散状态方程和伴随状态方程的块三角形Toeplitz结构研究者设计了一种快速梯度投影算法，提高了求解效率.

Antil H等人[9]提出了一类新的分数阶最优问题：分数阶抛物外部控制问题.由于分数阶算子的非局部性使得控制可以施加在外部区域，研究者便分别对Dirichlet和Robin最优控制问题进行了系统的分析，并通过数值算例进行了验证.Jin B T等人[19]研究了控制受限的时间分数阶最优控制问题的正则性及全离散有限元格式的先验误差估计，对时间方向离散采用了卷积积分和L1格式.

最近Wang T等人[20]研究了控制受限的带有非光滑初值的时间分数阶最优控制问题，对控制变量采用变分离散，建立了求解最优控制问题的全离散有限元格式，并分析了相应的误差估计，借助分层网格技术，获得了时间上的一阶精度.

3.1.2 空间分数阶最优控制问题 由于空间分数阶导数的定义方式不同，空间分数阶最优控制问题的形式也有多种.对于一维的双边分数阶扩散方程约束的最优控制问题，Zhou Z J等人[21]对带控制约束的空间分数阶最优控制问题进行了有限元逼近，在一阶最优性系统的基础上，证明了控制问题的正则性估计，并给出了状态、伴随状态和控制变量的先验误差估计，并基于离散状态方程和伴随状态方程系数矩阵的Toeplitz结构，构造了快速 Primal-dual Active Set算法，提高了有限元法的求解效率.

对于二维的分数阶控制问题，数值算法方面的研究工作主要集中在带有分数阶拉普拉斯算子的控制问题上.分数阶拉普拉斯算子的定义，常用的方式主要是积分形式定义和谱定义.对带有谱定义分数阶最优控制问题，Antil H等人[8,22-24]进行了一系列的研究，包括分布控制问题、稀疏控制问题等.由于谱定义的分数阶算子可以看做非一致椭圆算子的Dirichlet到Neumann 映射，为了避免直接对空间分数阶导数进行离散，利用Caffarelli-Silvestre延拓将空间分数阶方程转化为半无限圆柱上维数增加一维的非一致椭圆问题，从而将最优控制问题转化为等价的非一致椭圆型最优控制问题.非一致椭圆问题解的快速衰减使得截断方法在进行数值逼近时是一个合适的选择.基于此建立了有限元离散格式，并分析了相应的先验或后验误差估计理论.在文献[25]中，研究者将上述技术应用于一类空间分数阶导数的参数识别问题，建立了解的存在性及充分性条件，构建了半离散和全离散格式，并给出了收敛性分析.此外，Dohr S等人[26]研究了谱定义下分数阶拉普拉斯方程最优控制问题的有限元逼近问题.与 Antil H等人工作不同的是，Dohr S等人基于Balakrishnan公式计算状态方程解的近似，其中空间离散采用有限元法，额外涉及的积分采用sinc求积近似，并给出了控制变量采用变分方法离散和完全离散两种情况下的先验误差估计.

上述研究工作主要集中于控制变量受限问题，目前关于状态约束问题的研究工作还很少见.最近，Antil等人[30]研究了状态约束分数阶最优控制问题的有限元法逼近，借助Moreau-Yosida正则化技术，建立了状态约束分数阶最优控制问题的有限元离散格式及其相应的数值分析理论.Zhou Z J等人[31]研究了带积分状态约束的空间分数阶最优控制问题的有限元逼近问题并讨论了控制问题的一阶最优条件和正则性，导出了控制、状态、伴随状态和拉格朗日乘子的先验误差估计.由于分数阶导数的非局部性质导致离散状态方程和伴随状态方程系数矩阵的稠密，为了减少计算量，他们提出了一种基于系数矩阵Toeplitz结构的预处理快速投影梯度算法.

3.2谱方法分数阶导数具有非局部性，而谱方法通常采用全局基函数，所以是处理分数阶问题的有效方法之一.近年来谱方法被广泛地应用于求解分数阶微分方程及其约束的最优控制问题.

3.2.1 时间分数阶最优控制问题 Lotfi A等人[32]研究了Caputo型无约束分数阶最优控制问题的数值算法，该方法基于勒让德正交多项式基函数，将控制问题转化为一个代数方程组进行数值求解.Ye X Y等人[33]在无约束最优控制问题的框架下，运用谱方法求解了一类时间分数阶初值反问题，建立了目标函数最优解的唯一性和一阶必要最优条件，并提出了一种时空谱方法来数值求解得到的最优解问题，导出了谱逼近的先验误差估计.Ye X Y等人[34]进一步研究了状态积分约束的Caputo型时间分数阶最优控制问题的谱方法，建立了状态变量、控制变量的先验误差估计.Zaky M A等人[35]研究了求解无约束的时间分布阶最优控制问题的谱配置法，并建立了收敛性分析.上述研究工作采用的是传统的勒让德正交多项式.Li S Y等人[36]基于空间离散化的勒让德伪谱法和时间离散化的有限差分法，给出了时间分步扩散方程最优控制问题的数值解法，并利用拉格朗日插值基多项式逼近状态变量，得到了微分矩阵离散空间导数，讨论了控制问题的全离散格式.

3.2.2 空间分数阶最优控制问题 由于分数阶方程的解在边界处具有奇异性，为了适应奇异性，近年来研究者开始采用加权Jacobi多项式作为基函数去逼近分数阶方程的解[37,38]，该方法也被应用于分数阶最优控制问题.

文献[39]研究了一类空间Riesz分数阶最优控制问题的谱Galerkin逼近，分析了控制问题的解在加权Sobolev空间中的正则性，并采用加权Jacobi多项式作为基函数逼近状态变量，建立了加权范数意义下的先验误差估计.文献[40]讨论了带有积分形式的分数拉普拉斯式算子的分数阶对流扩散反应方程最优控制问题的谱Galerkin方法，分析了控制问题的解在加权Sobolev空间中的正则性，建立了加权范数意义下的最优先验误差估计.在上述工作基础上，文献[41]进一步研究了范数约束下分数阶对流扩散反应方程最优控制问题的谱Galerkin逼近，建立了加权范数意义下的最优先验误差估计.

最近，文献[42]研究了求解变扩散系数空间分数阶最优控制问题的谱方法，该方法采用加权Jacobi多项式作为基函数，依据先最优后离散的策略，构造了一种非直接谱方法.由于对于变扩散系数分数阶最优控制问题，传统的Galerkin变分形式不强制，给数值模拟带来困难.文献[42]中的方法可以有效的克服变系数所带来的困难.

3.3快速算法带约束的最优控制问题在数值离散后所得的代数系统是一个由离散状态方程、伴随方程及离散最优不等式耦合在一起的非线性系统，通常需要进行迭代求解.而分数阶导数的非局部性常导致离散后状态方程和伴随方程的系数矩阵不稀疏，这使得在数值迭代求解上述代数系统时的耗费比整数阶最优控制问题大很多，因此根据问题的特点设计快速计算方法是非常有必要的.

Du N等人[43]针对控制约束的分数阶扩散方程最优控制问题给出了Meerschaert和CN-WSGD两种有限差分格式, 并在传统的梯度投影算法的基础上利用Toepltiz矩阵的特殊结构提出了一种快速梯度投影算法，提高了求解效率.针对上述控制问题, Wu S L等人[44]提出并分析了时间并行算法，实现了梯度投影方法的快速计算，节省了计算时间.

Du N等人[45]针对具有确定性约束控制的随机空间分数阶扩散方程最优控制问题, 将梯度算法与随机Galerkin方法相结合，提出了一种快速随机Galerkin方法，有效地求解了非线性耦合系统.Wang F Y 等人[40]针对一类分数阶对流扩散反应方程最优控制问题，提出了快速的谱Galerkin近似.由于对流项和反应项的存在，离散状态方程和伴随方程的离散矩阵不再稀疏.为了提高求解效率，他们采用快速多项式变换来计算矩阵和向量的乘积，构造了快速投影梯度算法，提高了求解效率.

4 研究展望

近年来，针对分数阶方程约束最优控制问题，已取得了一系列优秀的研究成果，然而仍有许多问题尚未解决.

首先，分数阶最优控制问题解的适定性理论仍需完善，包括解的正则性等在内的一些理论尚不清楚，而这些理论是数值分析的基础.

其次，关于状态约束问题、边界或者外部控制问题方面的工作还很少.对于带有变扩散系数的分数阶最优控制问题[41],虽然已经进行了初步尝试，但仍有许多问题亟待解决.

最后，离散代数系统的快速优化迭代算法仍需研究.对分数阶问题，特别是高维的问题，如何针对问题的特征设计快速的优化迭代算法，提高计算效率，是一个非常有意义的研究领域.