解题应重视自然而至简的通解通法——从一道二元二次函数最值题的研究谈起

刘海涛

(安徽省芜湖市第一中学 241000)

1 试题呈现与分析

题目已知5x2y2+y4=1(x,y∈R)，则x2+y2的最小值是____．

分析该题形式上以二元方程为背景命题，主要考查分析、解决二元问题的能力，强化对转化与化归、函数与方程、消元与不等式求最值等数学思想方法的考查，体现了逻辑推理、数学运算等数学核心素养.试题结构虽简单、明了，但内涵丰富，本文尝试对该题从不同的角度予以思考，给出不同的解法.

2 解法探究

角度1整体处理，借助不等式求最值.

解法1(配凑+基本不等式法)由5x2y2+y4=1，得y2(5x2+y2)=1.

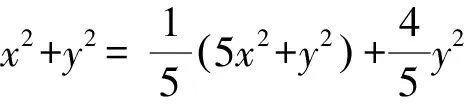
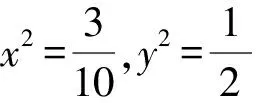
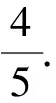
评注通过代数化简，将问题转化为y2与5x2+y2的问题，条件式为两者积为定值，目标式是与两者有关的和，自然想到借助基本不等式求解.

解法2 (待定系数+基本不等式法)

由(x2+y2)2=x4+2x2y2+y4，

设(x2+y2)2=x4+ty4+2x2y2+(1-t)y4，

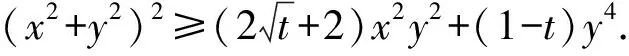
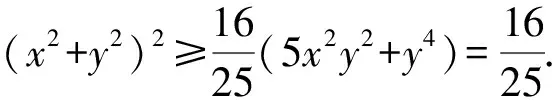
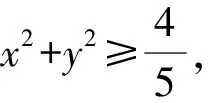
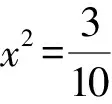
评注在得到(x2+y2)2=x4+2x2y2+y4后，联想利用不等式将其放缩为5x2y2+y4的倍数，但是这里对系数的配凑不太容易，于是考虑待定系数法.利用待定系数法配凑，再借助不等式求最值的方法，往往可以降低配凑系数带来的思维难度，读者在日常的解题中可以尝试该法的使用.

角度2化二元为一元，转化为一元函数最值问题.

解法3 (消元+基本不等式法)

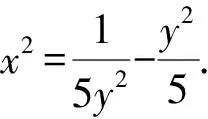
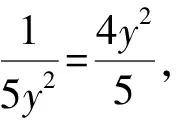
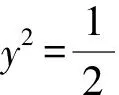
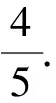
评注化二元为一元是解决二元函数的最直接做法，通法是消去其中一个变量，得到关于另一变量的函数，接着利用不等式、对勾函数等求出最值.

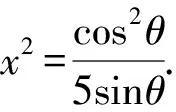
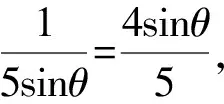
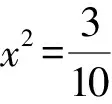
评注由条件式平方和为1的结构特征，联想cos2θ+sin2θ=1，所以想到利用三角换元，将二元(x,y)问题转化为一元(θ)问题，根据目标式特点选择合适方式求最值.

解法5(三角换元+函数最值法)令x2+y2=r2，由5x2y2+y4=1知x,y至少有一个不为0.

设x=rcosθ，y=rsinθ，代入5x2y2+y4=1，整理,得

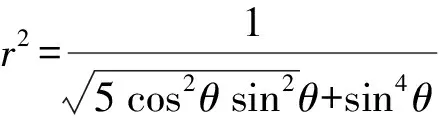
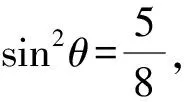
评注着眼于目标式特征，由于x,y至少有一个不为0，故设x=rcosθ，y=rsinθ，于是问题转化为三角函数问题，顺利实现减元，利用一元二次函数知识即可求出最值.

解法6(齐次化+基本不等式法)

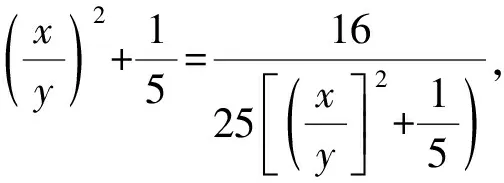
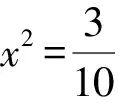
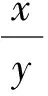
角度3 着眼于目标式，借助方程判别式.

解法7 (判别式法)设x2+y2=t(t>0)，则x2=t-y2.

代入5x2y2+y4=1，整理,得

关于y2的一元二次方程4y4-5ty2+1=0.

方程有解的充要条件为Δ=(-5t)2-16≥0，

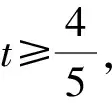
评注将目标式设为参数t，利用t将条件式转化为关于y2的一元二次方程，将问题转化为方程有解问题，借助判别式解题.

角度4 回顾函数本质，多元函数找对策.

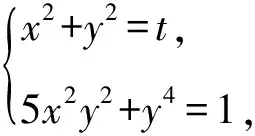
对x求导,得

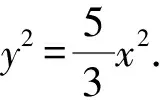
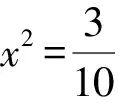
解法9(拉格朗日乘数法)构造函数f(x,y,λ)=x2+y2+λ(5x2y2+y4-1)，令f(x,y,λ)对x,y,λ的一阶偏导数为零，则

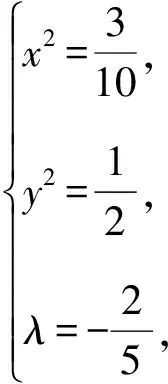
评注函数偏导法与拉格朗日乘数法都是高等数学背景下的解法，提供给读者参考.

3 变式推广，总结通解通法

若令x2=u，y2=v，则问题等价于：已知5uv+v2=1，求u+v的最小值.我们不难发现，问题的实质为以二元二次方程为背景的二元函数最值问题，类似问题频繁出现在高考和各类模拟考中，笔者经过整理，将此类问题根据条件式或目标式特征进行分类，并据此特征总结通解通法.

3.1 条件式为(ax+b)(cy+d)=m的二元最值问题

例1 若正实数x,y满足xy-2x-y=6，则xy的最小值为____.

解析由xy-2x-y=6,得(x-1)(y-2)=8.

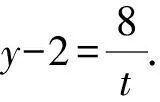
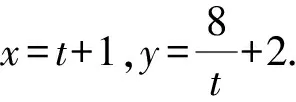
例2 设x,y∈R，且满足4x+y+2xy+1=0，则x2+y2+x+4y的最小值为____.

解析由4x+y+2xy+1=0,

得(2x+1)(y+2)=1.

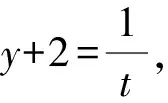
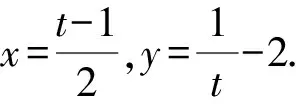
所以x2+y2+x+4y

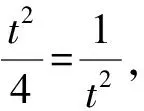
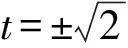
方法归纳一般地，若已知实数x,y满足(ax+b)(cy+d)=m(a,b,c,d,m均为非零实数)，求二元函数f(x,y)的最值，通法步骤为：

(2)将(1)中所得结果代入二元函数f(x,y)，得到关于t的一元函数；

(3)利用函数或不等式等方法解(2)中所得关于t的函数的最值.

3.2 条件式为(ax+by)(cx+dy)=m的二元最值问题

例3已知实数x,y满足5x2-y2-4xy=5，则2x2+y2的最小值等于( ).

解析由5x2-y2-4xy=5,得

(5x+y)(x-y)=5.

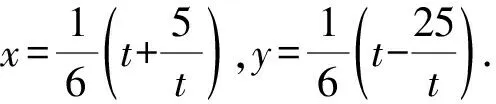
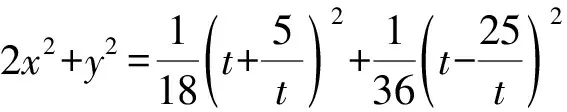
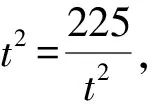
例4 已知正实数x,y满足2x2+2y2+5xy=1，则xy+x+y的最大值为____.

解析由2x2+2y2+5xy=1,

得(2x+y)(x+2y)=1.

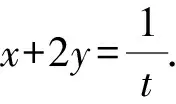
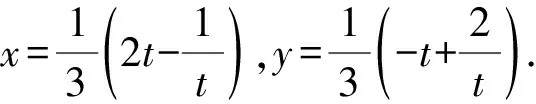
所以xy+x+y

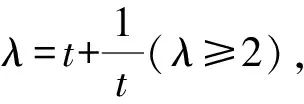
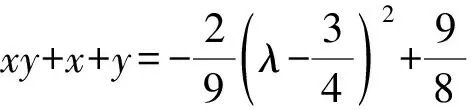
在λ∈[2，+∞)上单调递减.

方法归纳一般地，若已知实数x,y满足(ax+by)(cx+dy)=m(a,b,c,d,m均为非零实数，且ad≠bc)，求二元函数f(x,y)的最值，通法步骤为：

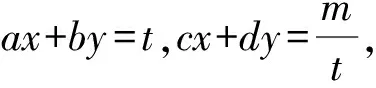
(2)将(1)中所得结果代入二元函数f(x,y)，得到关于t的一元函数；

(3)利用函数或不等式等方法解(2)中所得关于t的函数的最值.

3.3 条件式为(ax+by)2+(cx+dy)2=m的二元最值问题

例5 若正数x,y满足x2+y2+xy=9，则x+2y的最大值为____.

解析由x2+y2+xy=9,得

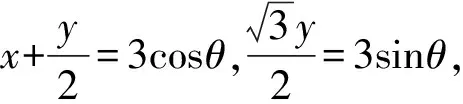
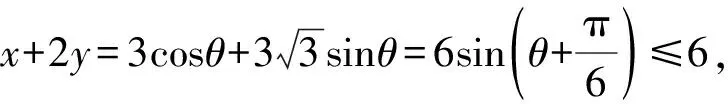
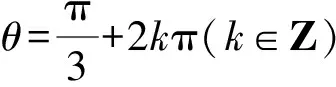
例6 已知x,y∈R，且满足x2+4y2+2xy=6，求z=x2+4y2的最值.

解析由x2+4y2+2xy=6,得

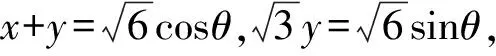
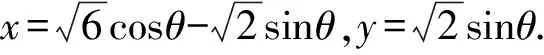
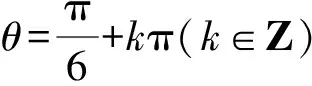
方法归纳一般地，若已知实数x,y满足(ax+by)2+(cx+dy)2=m(a,b,c,d均为非零实数，m为正实数，且ad≠bc)，求二元函数f(x,y)的最值，通法步骤为：

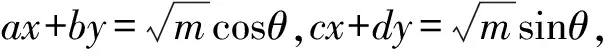
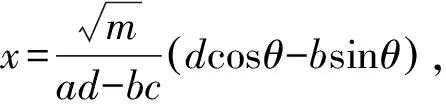
(2)将(1)中所得结果代入二元函数f(x,y)，得到关于θ的一元函数；

(3)利用三角函数或不等式等知识解(2)中所得关于θ的函数的最值.

3.4 目标式为ax+by的二元最值问题

例7 已知正数x,y满足x+2y+2xy=8，则x+2y的最小值是( ).

解析设x+2y=t(t>0)，则x=t-2y.

代入x+2y+2xy=8，整理,得

关于y的方程4y2-2ty+8-t=0(y>0).

方程有解的充要条件为

Δ=(-2t)2-16(8-t)≥0，

解得t≥4，

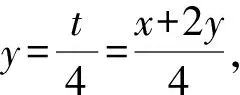
即x=2y时等号成立.

所以x+2y的最小值为4.

方法归纳一般地，若已知二元二次方程f(x,y)=0，求二元一次函数ax+by(a,b均为非零实数)的最值，通法步骤为：

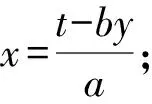
(2)将(1)中所得结果代入二元二次方程f(x,y)=0，得到关于y的一元二次方程；

(3)利用判别式解(2)中所得关于y的方程有解对应的t的取值范围，验证等号成立取得所求最值.

3.5 目标式为ax2+by2的二元最值问题

例8 若实数x,y满足x2+2xy-y2=7，则x2+y2的最小值为____.

解析设x2+y2=r2，易知x,y不同时为0，所以r≠0.

设x=rcosθ，y=rsinθ，代入x2+2xy-y2=7，

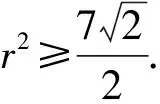
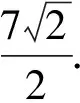
方法归纳一般地，若已知二元方程f(x,y)=0，求二元二次函数ax2+by2(a,b>0)的最值，通法步骤为：

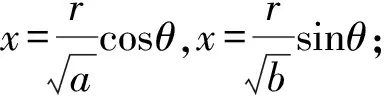
(2)将(1)中所得结果代入二元方程f(x,y)=0，得到关于θ的方程；

(3)利用三角函数的有界性等知识解(2)中所得关于θ的方程，得到关于r2的不等式，得到r2的取值范围，即得ax2+by2的最值.

4 教学启示

数学解题的目的是什么？是求出问题的答案吗？是，但不全是！解题的目的是巩固数学基础知识、落实数学基本技能、感悟数学思想方法、提升数学思维活动经验，所以对一道典型问题，尤其是高考题的多角度分析与解答是非常有必要的.用多种方法解答同一道数学题，不仅能更牢固地掌握相关的数学知识，还能更灵活地运用所学知识．通过一题多解，分析、比较各种解法，可以找到最佳的解题途径，从而发散学生的思维能力，对巩固知识和解题能力大有裨益，是提高数学成绩的一条捷径．

当然并非解法越多越好，在寻求多解的过程中要突出通性、通法的辐射、迁移的作用，要追求水到渠成、自然而然的解题方法.正如数学家加德纳说：“数学的真谛在于不断寻求越来越简单的方法证明定理和数学问题”.笔者认为这里所谓的“简单”，不是指特殊的技巧，或书写过程的简洁，而是解答一道问题的思维过程是自然的、简单的，运用的知识也是基础的，正所谓“大道至简”，因此文章中将近些年一些高考和模拟考中的关于二元最值题，按照条件式或者目标式的结构特征进行分类，总结其通解通法，以求让学生能“做一题，通一类”，真正实现“一题多解，多解归一”.另外，笔者认为在日常的教学中，教师还要指导学生结合自身掌握程度和实际情况，选择最佳的解题方法，不要一味追求某一种解法，要学会从不同解法中汲取不同的数学思想，提高自身的数学核心素养.