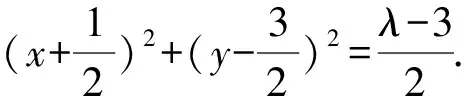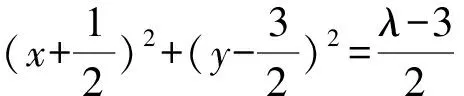二次曲线系在圆锥曲线四点共圆问题中的应用

李鸿昌

(贵州省贵阳市北京师范大学贵阳附属中学 550081)

1 预备知识

1.1 二次曲线系

两个二次曲线通常有四个交点(这些交点中可能有重合的，也可能有虚的).如果这两个二次曲线的方程分别为f1(x,y)=0和f2(x,y)=0(fi(x,y)=0是x,y的二次式)，那么过它们交点的二次曲线束可写成λf1(x,y)+μf2(x,y)=0，其中λ,μ为实数且不全为0.

当二次曲线退化为直线时，即得到直线束方程.

1.2 直线系方程

设直线l1:m1x+n1y+c1=0与直线l2:m2x+n2y+c2=0相交于点P，则过点P的直线束方程可写成λ(m1x+n1y+c1)+μ(m2x+n2y+c2)=0,其中λ,μ为实数且不全为0.

特别地，过点P的曲线束方程为(m1x+n1y+c1)(m2x+n2y+c2)=0.

1.3 圆系方程

过两条直线f1=0,f2=0与一条二次曲线f(x,y)=0的4个交点的二次曲线束方程为f(x,y)+λf1f2=0(λ为参数)，仅当此方程中x2与y2的系数相同时表示圆.

2 典例分析

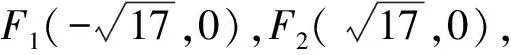
(1)求C的方程；

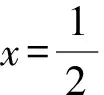
解析(1)因为|MF1|-|MF2|=2，所以M的轨迹C为双曲线的右支，且

c2=17，2a=2，c2=a2+b2，

解得a=1，b=4.

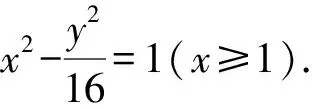
(2)由|TA|·|TB|=|TP|·|TQ|，得

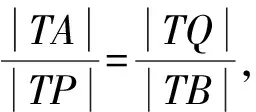
所以△ATQ∽△PTB.

从而∠ABP=∠AQP.

因此A,B,Q,P四点共圆.

由题意知，直线AB和PQ的斜率均存在且不等于0，则直线AB的方程为

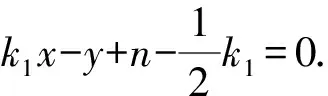
同理直线PQ的方程为

则过A,B,Q,P四点的二次曲线系方程为

(*)

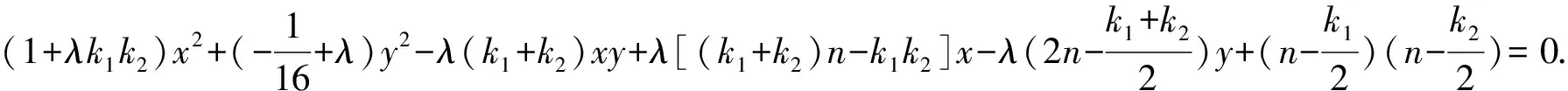
因为A,B,Q,P四点共圆，所以该圆也是曲线(*)中的一条曲线.

方程(*)为圆的充要条件是

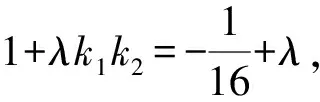
因为λ≠0，

所以k1+k2=0.

因此直线AB的斜率与直线PQ的斜率之和等于0.

点评根据双曲线方程及直线AB和PQ的方程，可写出过A,B,Q,P四点的二次曲线系方程. 再由条件“|TA|·|TB|=|TP|·|TQ|”得到A,B,Q,P四点共圆，所以二次曲线系方程中x2与y2的系数相同，从而得到k1+k2=0.

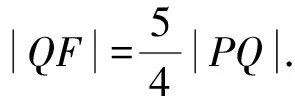
(1)求C的方程；

(2)过点F的直线l与C相交于A,B两点，若AB的垂直平分线l′与C相交于M,N两点，且A,M,B,N四点在同一圆上，求l的方程.

解析(1)设Q(x0,4)，代入y2=2px,得

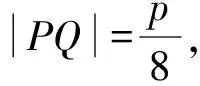
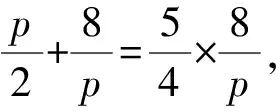
解得p=2.

所以C的方程为y2=4x.

(2)由题意知直线l与x轴不垂直，故可设l的方程为x=my+1.

故可设AB的垂直平分线l′的方程为

于是过A,M,B,N四点的二次曲线系方程为

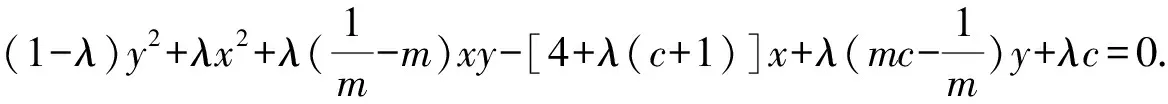
因为A,M,B,N四点共圆，

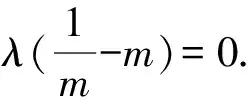
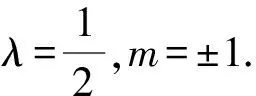
故直线l的方程为

x-y-1=0或x+y-1=0.

点评由题意可设出l和l′的方程，然后写出过A,M,B,N四点的二次曲线系方程，根据A,M,B,N四点共圆，知方程中x2与y2的系数相同且xy的系数为0，从而得到l的方程.

3 应用

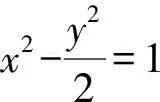
(1)求直线AB的方程；

(2)如果线段AB的垂直平分线与双曲线相交于C,D两点，那么A,B,C,D四点是否共圆，为什么？

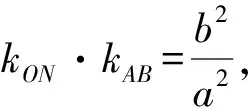
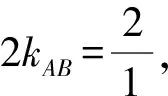
所以直线AB的方程为y-x-1=0.

(2)易知直线CD的方程为y+x-3=0.

所以过A,B,C,D四点的二次曲线系方程为

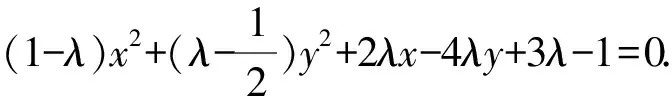
该曲线方程表示圆的充要条件是

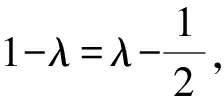
此时圆的方程为x2+y2+6x-12y+5=0.

因此A,B,C,D四点在圆x2+y2+6x-12y+5=0上，即A,B,C,D四点共圆.

题2(2005年湖北卷)设A,B是椭圆3x2+y2=λ上的两点，点N(1，3)是线段AB的中点，线段AB的垂直平分线与椭圆相交于C,D两点.

(1)确定λ的取值范围，并求直线AB的方程；

(2)试判断是否存在这样的λ，使得A,B,C,D四点共圆？并说明理由.

解析(1)由于点N(1，3)是线段AB的中点，

所以N(1，3)在椭圆3x2+y2=λ内.

故3×12+32<λ，

即λ>12.

因此λ的取值范围是λ∈(12,+∞).

3kAB=-3，即kAB=-1.

所以直线AB的方程x+y-4=0.

(2)易知直线CD的方程为x-y+2=0.

所以过A,B,C,D四点的二次曲线系方程为

3x2+y2-λ+μ(x+y-4)(x-y+2)=0.

即(3+μ)x2+(1-μ)y2-2μx+6μy-8μ-λ=0.

该曲线方程表示圆的充要条件是

3+μ=1-μ，即μ=-1.

此时圆的方程为