BBM方程的精确行波解研究
刘红霞,韩青秀,伍 芸,于亚峰
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
考虑如下的BBM方程
(1)
其中α,β,γ是常数。方程(1)是由 Benjamin等[1]于 1972年提出的一个正则化的非线性长波方程,该方程是一个改进的 KdV 方程。主要用于对(1+1)维上单向传播的小振幅重力波进行建模。文献[1-4]从不同方面对方程展开了研究并获得BBM方程在不同参数条件下的显示解。文献[5]利用符号计算得到了BBM方程丰富的行波解。目前求解非线性方程精确解的方法主要有首次积分法、动力系统分支理论[6-7]、各种函数展开法和辅助函数法[8-10]、齐次平衡法[11]。动力系统分支理论在我们的研究中起到非常重要的作用,获得的精确解不仅在物理科学中有着非常重要的作用,也有助于进一步了解该模型所描述的物理现象。而本文主要应用微分方程定性理论与动力系统分支方法,求解方程(1)的非线性行波解,并在不同的参数条件下,得到不同于文献[3]的行波解的精确参数表示。
为了研究方程(1)的非线性波,设c>0是波速,u(x,t)=φ(ξ),ξ=x+ct。将u=φ(ξ)代入BBM方程可得
cφ′+αφ′+βφφ′-cγφ‴=0
(2)
对(2)式两边积分可得
(3)
其中g是积分常数且g≠0。
令φ′=y,可得到下面的平面系统
(4)
其中k=c+α。
很明显,系统(4)是一个有着Hamiltonian函数的Hamiltonian系统
(5)
如果令
则我们有下面的结果:
当Δ>0时,f(φ)有2个零点φ1和φ2,它们的表达式为
(6)
当Δ=0时,f(φ)有1个零点φ0,它的表达式为
当Δ<0时,f(φ)没有零点。

利用微分方程动力系统的定性理论,我们有下面的结论。
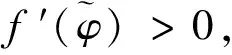
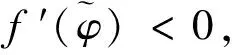

1 BBM方程的行波解的精确参数表达式
命题1 在如下任一情形时:
1)g>0,γ>0,β>0,k>0;
2)g>0,γ>0,β>0,k<0;
3)g<0,γ>0,β>0,k>0;
4)g<0,γ>0,β>0,k<0。
(7)
(8)
其中
证明在(5)式中,令H(φ1,0)=h1,则有
(9)
由(4)式得
(10)
积分(10)式有
(11)
同理,在(5)式中,令H(φ2,0)=h2,则有
(12)

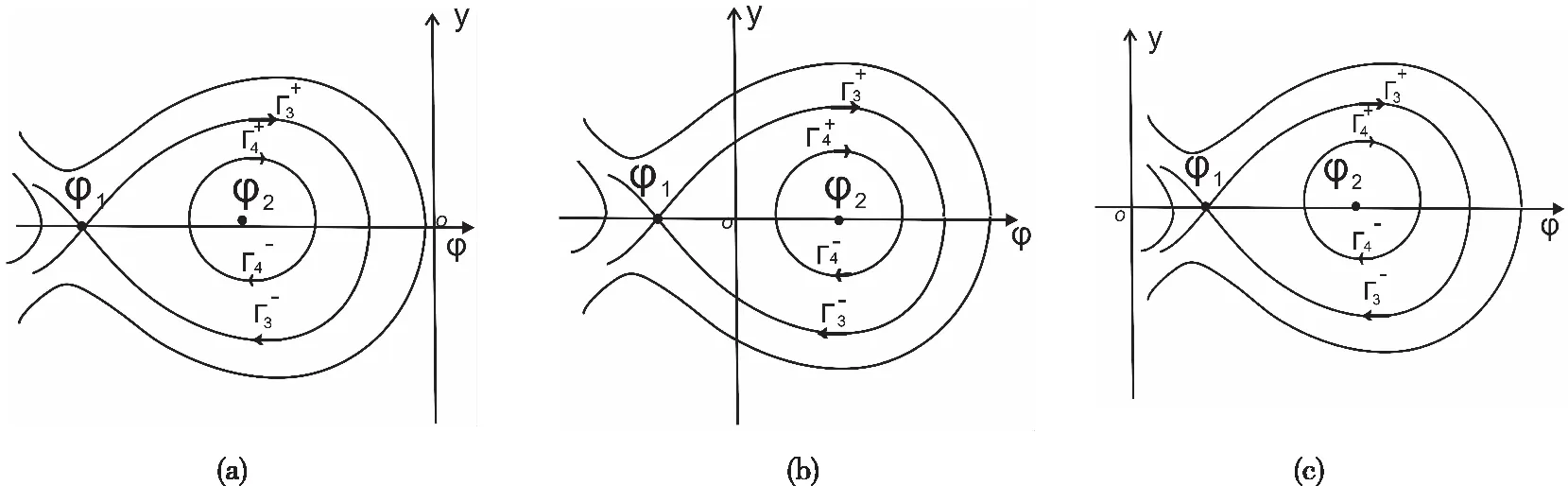
图和的轨道图
由(4)式可得
(13)
积分(13)式有
(14)
命题2 在如下任一情形时:
1)g>0,γ>0,β<0,k>0;
2)g>0,γ>0,β<0,k<0;
3)g<0,γ>0,β<0,k>0;
4)g<0,γ>0,β<0,k<0。
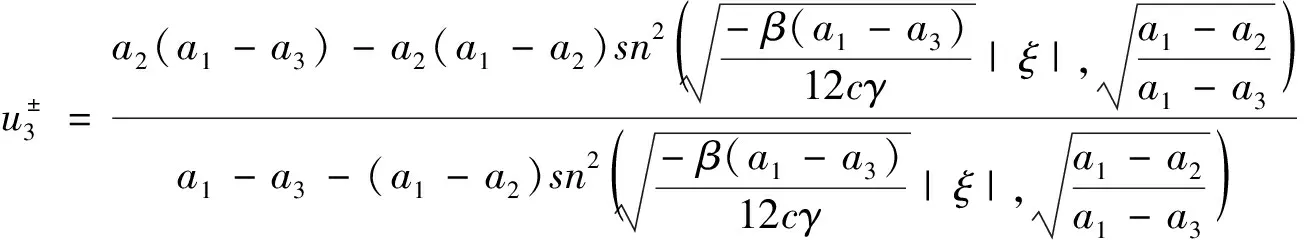
(15)
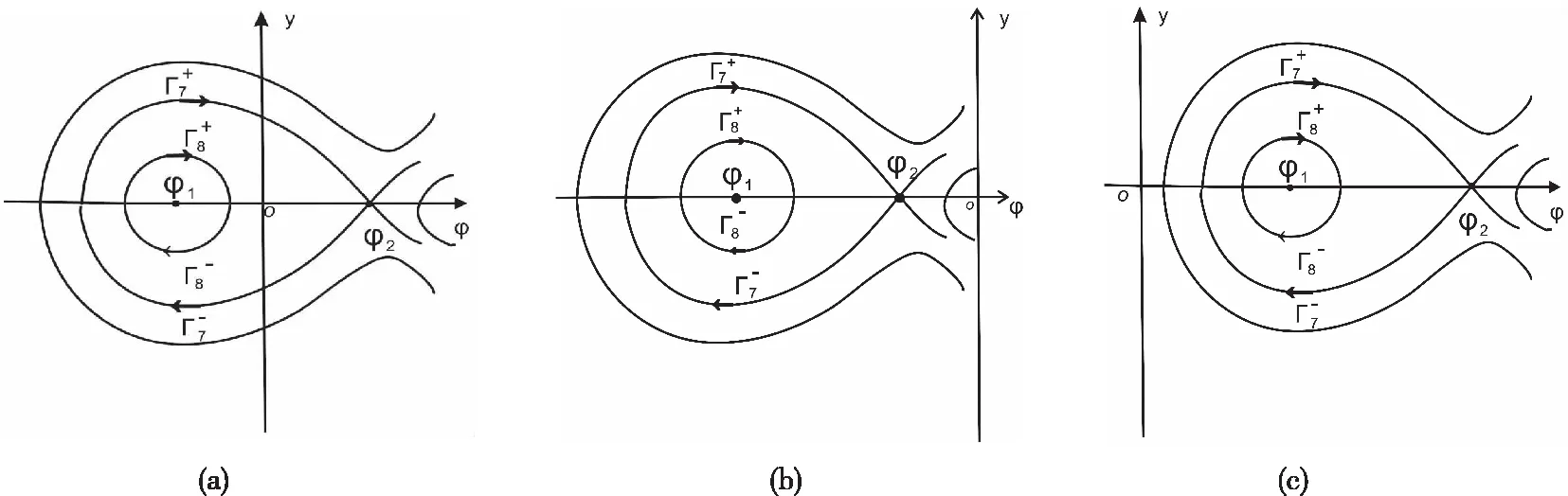
图和的轨道图

证明在(5)式中,令H(φ1,0)=h1,则有
(16)
由(4)式得到
(17)
同理,在(5)式中,令H(φ2,0)=h2则有
(18)
由(4)式可得
(19)
对(19)式积分得
(20)
命题3 在如下任一情形时:
1)g>0,γ<0,β>0,k>0;
2)g>0,γ<0,β>0,k<0;
3)g<0,γ<0,β>0,k>0;
4)g<0,γ<0,β>0,k<0。
(21)
其中

图和的轨道图

证明 在(5)式中, 令H(φ2,0)=h2,则有
(22)
由(4)式可得
(23)
积分(23)式得
(24)
同理,在(5)式中,令H(φ1,0)=h1,则有
(25)
由(4)式可得
(26)
命题4 在如下任一情形时:
1)g>0,γ<0,β<0,k>0;
2)g>0,γ<0,β<0,k<0;
3)g<0,γ<0,β<0,k<0;
4)g<0,γ<0,β<0,k>0。
证明在(5)式中,令H(φ2,0)=h2,则有
(27)
同理,在(5)式中,令H(φ1,0)=h1,则有
图和的轨道图
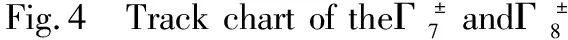

(28)

