解析几何“搭台”，核心素养“唱戏”——以2021 年全国新高考Ⅰ卷解析几何解答题为例

文/岭南师范学院附属中学 谢飞燕

《普通高中数学课程标准（2017 年版2020 年修订）》指出：在学习数学和应用数学的过程中，学生能发展数学抽象、数学建模、逻辑推理、数学运算、数据分析、直观想象等数学学科核心素养.因此，我们让学生在学习数学知识的过程中如何发展并形成核心素养，是新一轮课程改革的任务.培养学生数学核心素养要贯彻到每一节课中，落实到每一道题的解决过程之中，细化到每道题的每个步骤.下面以2021 年全国新高考Ⅰ卷解析几何解答题为例，通过解析几何问题的解答探究提出课堂教学中如何提升学生的数学核心素养，正所谓解析几何“搭台”，核心素养“唱戏”.

一、试题再现

（2021 年全国新高考Ⅰ卷第21 题）在平面直角坐标系xOy 中，已知点0），|MF1|-|MF2|=2，点M 的轨迹为C.（1）求C 的方程；（2）设点T在直线上，过T 的两条直线分别交C 于A、B 两点和P，Q 两点，且|TA|·|TB| = |TP|·|TQ|，求直线AB 的斜率与直线PQ 的斜率之和.

二、解法探究

1.第一问解法分析

分析1：第一问利用双曲线的定义可知轨迹C 是以点F1、F2为左、右焦点的双曲线的右支，求出a、b 的值，即可得出轨迹C 的方程.

解法1：因为|MF1|-|MF2| =2所以，轨迹C 是以点F1、F2为左、右焦点的双曲线的右支，设轨迹C 的方程为=1（a＞0，b＞0），则2a=2，可得a=所以，轨迹C 的方程为

评析：掌握了双曲线的定义，才能辨别出问题的条件与定义的不同之处，准确不漏地写出轨迹C的方程.不少考生可能忽略了双曲线定义中的“绝对值”字眼而误认为轨迹C 是双曲线，这充分暴露了考生在解析几何方面严重缺乏数学抽象的核心素养所以对双曲线的定义未能真正地理解，未能从双曲线的标准方程中抽象出双曲线的两支，题中的轨迹C 只是双曲线的右支，并非整条双曲线.

分析2：第一问也可以用解析法，根据求轨迹的步骤，先设出点C 的坐标（x，y）根据题中的等式，代入坐标得到关于x，y 的方程并化简则可得出轨迹C 的方程.

解法2：设点C（x，y），∵|MF1|-

评析：解析几何法的基础是解析法，解法2 回归原始的解析几何思想，学生只要回忆之前推导椭圆的标准方程时的那段“艰苦”的历程，重复体验一下那两次平方的过程即可.当然这里的化简过程考察了考生的数学运算核心素养，并且要求不低，会算可能也会出错，即“会而不对”.解析法遵循“建立坐标系—设点—列出限制【 —代入坐标—化简—检验”等步骤，一般情况下最后一步可以省略，所以坐标法步骤简称“建设现（限）代化”五个步骤，但此题最后一步必不可少，不少考生没有检验从而忽略了化简过程中的隐藏【 x＞0导致得出不完整的答案.

2.第二问解法分析

设直线PQ 的斜率为k2，同理可得因为|TA|·|TB| = |TP|·|TQ|，即整理可得，即（k1-k2）（k1+k2）=0，显然k1-k2≠0，故k1+k2=0.

评析：圆锥曲线综合问题常用的“设直线方程—联立方程组—消元—韦达定理……”解题策略，对于第二问，大部分考生都能完成前四步，但又只能到此“望题兴叹”了.因为按照两点间的距离公式代入运算非常复杂，对学生的运算要求很高，此时优化运算变得尤为重要.我们孰悉的圆锥曲线弦长公式其实是直线上两点间的距离公式，若A（x1，y1），B（x2，y2）是直线y=kx+b（k ≠0）的两点，则| AB | =

分析2：因为题中涉及两个线段的长度的乘积，可以借用向量的数量积解决问题，由T，A，B 三点共线可知，现利用向量的坐标运算和前面得到的根与系数的关系求解.

评析：整体考虑|TA| |TB|，利用向量工具解决问题可以避免运用弦长公式在运算过程中出现绝对值或根号等象征着复杂运算的符号，运用向量作为工具解决解析几何问题是常用方法之一.

分析3：考虑到第二问中的|TA|和|TB|为过点T 的直线与双曲线的交点所形成的线段的长度，利用点T 建立直线的参数方程，根据参数方程中t 的几何意义可快速求得|TA|和|TB|，可以简化部分数学运算.

代入双曲线可得（16 cos2αsin2α）t2+（16cosα-2msinα）t-12-m2=0

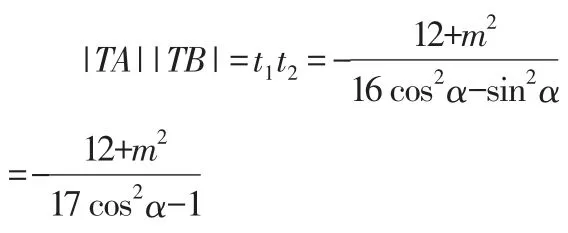
因为| TA | · | TB | = |TP| ·|TQ|，所以cos2α=cos2β.

则cosα+cosβ=0，所以α=π-β即两斜率和为零.

评析：引入参数，用直线的参数方程或曲线参数方程中参数的几何意义搭起题目中量与量之间的关系，建立方程进行运算求解，这是解析几何中常用的方法，但可能是学生们对参数方程的学习不够，很少能把解析几何问题与参数方程联系一起，特别是在新高考中取消了最后一道大题即往年的选做题后，学生对参数方程更陌生了.

3.教学思考

加强学生对解析几何知识本质的理解，提升其数学抽象与直观想象素养.注重学生的运算能力培养，提升其数学运算核心素养.探索数学中几何关系如何代数化的途径，提升学生逻辑推理素养.