基于GRNN的光谱共焦位移测量方法分析与研究

李春艳，李庚鹏，刘继红，罗豆，刘佳奕

（西安邮电大学电子工程学院，西安710121）

0 引言

光谱共焦技术利用色散原理实现光学微位移的非接触式精密测量。与激光三角测量［1］、激光干涉测量［2］、光栅干涉［3］等测量技术相比，光谱共焦技术以超高的测量分辨率实现多表面层析探测，同时不受物体表面弯曲、倾斜影响，普遍适用于各种环境及材料。该技术使用宽谱光源通过色散物镜产生轴向色差，建立光谱波长焦点位置与波长间精确的对应关系，利用光谱仪探测聚焦于物体表面反射回来的色散光谱的峰值波长，实现物体表面轴向位置的精确测量［4-7］。光谱仪探测到的光谱数据受到诸多因素影响：1）色散物镜未经校正的单色像差；2）光源及分光系统的光谱依赖性；3）光谱信号离散采样间隔的限制；4）光谱仪的器件噪声、暗电流噪声等。对光谱信号的归一化光强最大值点处的波长进行直接提取，并解算对应的焦点位置，容易使峰值波长与焦点位置的映射关系出现不可忽略的非线性，造成色散模型的波动进而引起高度相关的测量误差［8-10］。光谱共焦技术由激光扫描共焦显微镜（Laser Scanning Confocal Microscopy，LSCM）发展而来，LSCMs 技术利用轴向光强响应特性曲线峰值位置对应于光学系统的物镜焦点位置的原理实现位置测量，它们有着类似的峰提取方法。传统的寻峰方法包括最值法、质心法、高斯拟合法等［11］。最值法适用于理想状态下的光谱信号，质心法适合对称信号的峰值寻找，高斯法适合形如高斯分布的信号，光谱共焦系统的出射光光谱波峰受到器件噪声等干扰，呈非对称分布，不完全遵循高斯分布。TAN J B 提出了一种基于sinc2的光谱拟合算法［12］，实现LSCMs 表面形貌测量过程中的峰值提取，但是光谱共焦系统的测量过程不经过轴向扫描操作，光轴上的光强分布不遵循sinc2分布，反射光谱也比LSCMs 更宽、更不规则。神经网络是一种常用的处理非线性问题的方法，目前神经网络方法已广泛应用于光学领域中确定输入与输出响应的关系，如光谱仪、数码相机或传感器的校准等方面［13］。广义回归神经网络（General Regression Neural Network，GRNN）是一种以概率密度函数为基础的径向基网络，训练简洁、收敛速度快，非线性映射精度高［14-15］。本文将采集到光谱信号作为样本数据输入GRNN 模型，实现光谱共焦系统的轴向信号响应曲线的表征，提高反射光谱的信噪比，并通过提取GRNN 模型表征的光谱曲线峰值波长，修订色散波长与焦点位置之间的对应关系，提高系统测量的分辨率与稳定性。

1 光谱共焦测量系统

如图1所示，光源发出宽光谱复色白光，经色散系统产生轴向色散，在一定范围内的出射光轴上，形成了单色聚焦位置Zmin～Zmax与各光谱色散光波波长λmin～λmax之间的精确对应关系。

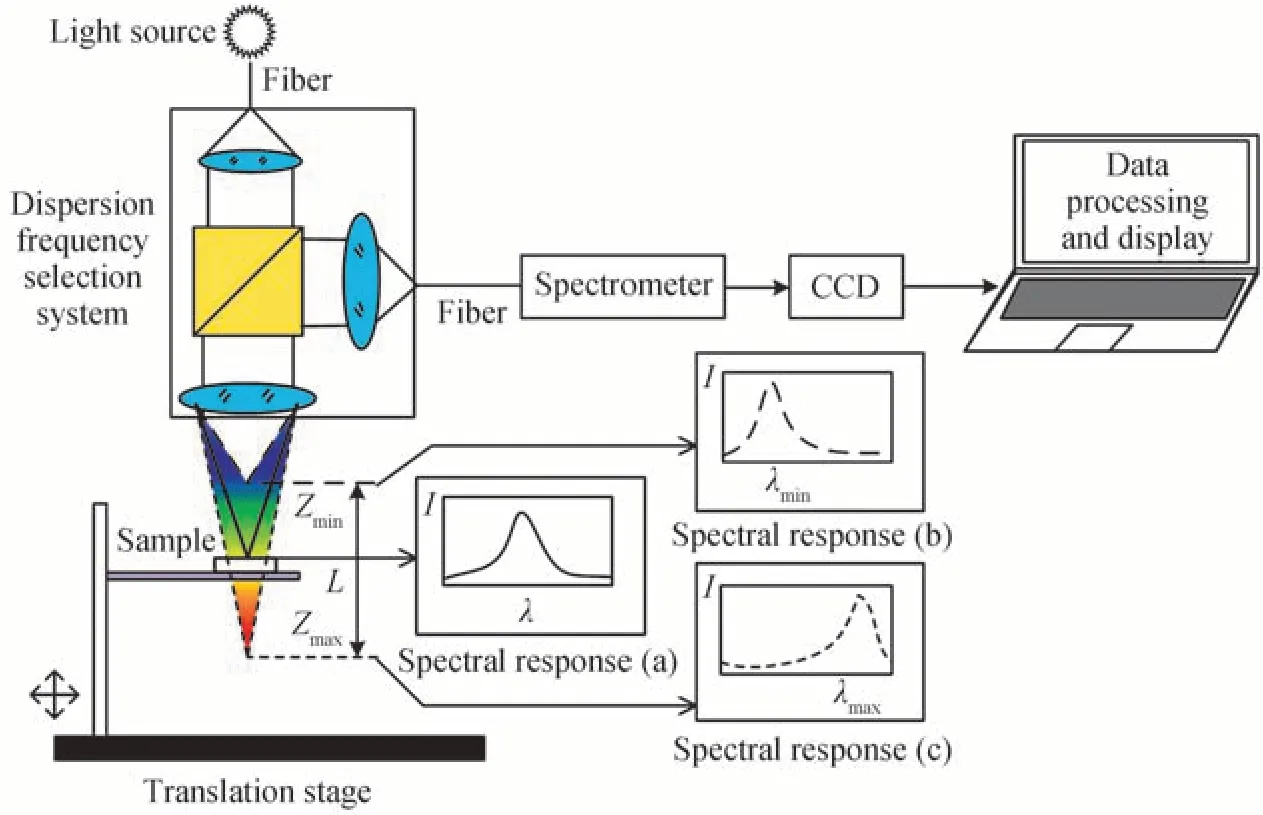
图1 光谱共焦位移传感器原理Fig.1 Schematic diagram of spectral confocal displacement sensor

当被测样品位于光源的色散范围内，样品表面反射回特定的色散光波λ，其他光波无法在样品表面聚焦而形成弥散斑，反射后能够通过分光器件、圆孔光阑等到达光谱仪的光能极弱。如图1所示，被测样品表面的聚集色散光波λ在返回的光谱响应（a）中以波峰形式呈现，通过反解波长λ，即可实现样品表面轴向位置的精确测量。当色散光波λmin与λmax分别聚焦于轴向位置点Zmin与Zmax处，则分别对应图1 中的光谱响应（b）、（c），色散范围对应的轴向间距L，即为可测量的位移范围。

2 GRNN 理论基础及网络结构

广义回归神经网络是一种基于径向基函数，高度并行式的前馈网络模型。该网络利用样本数据输入变量X与输出变量Y的联合概率密度函数f（X，Y）作为后验条件，对预测输出进行Parzen 非参数核回归，得到输出变量Y的最大概率输出值为

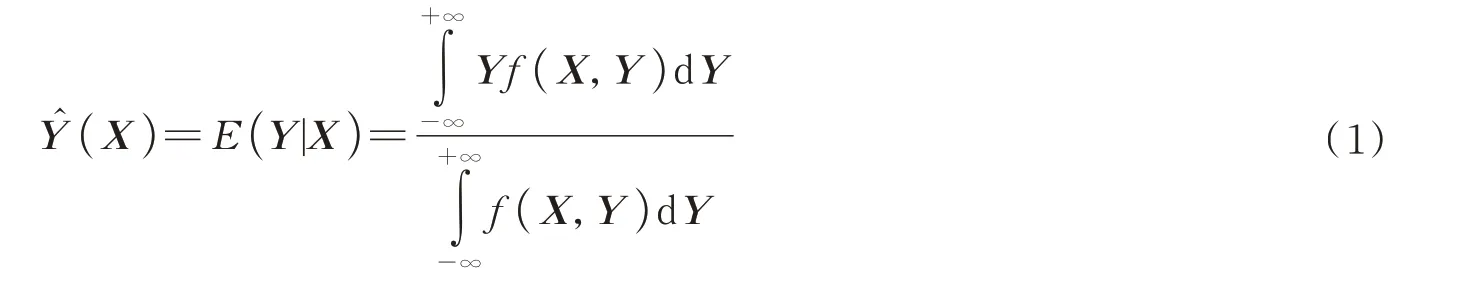
式中的联合概率密度函数f(X，Y)为

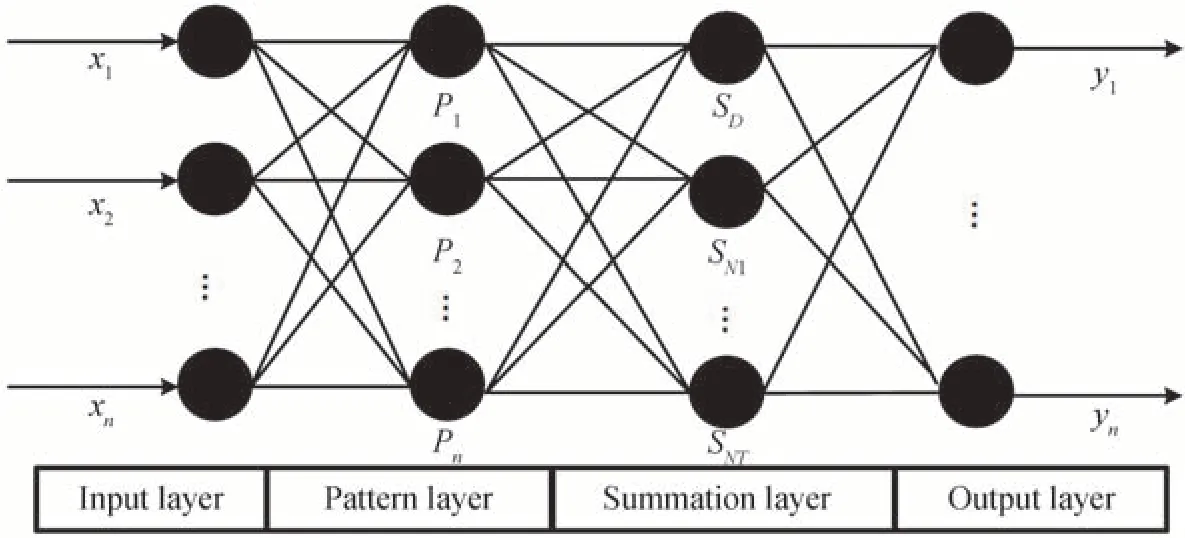
图2 广义回归神经网络结构图Fig.2 Structure diagram of generalized regression neural network

3 实验验证

本文将采集到的光谱数据作为GRNN 网络的样本数据，其中光谱信号的波长λ作为GRNN 模型的输入变量，波长对应的归一化强度（Normalized Intensity）作为输出变量，利用基于概率密度函数的非参数核回归，得到波长对应的归一化强度的最大概率输出值，重新拟合光谱曲线。由于GRNN 网络的样本输出将样本点附近的样本数据的权重考虑在内，一定程度上能够消除光谱信号随机噪声的影响，提高光谱信噪比的作用，进而抵消光谱信号由于一系列影响因素引起的表征误差。

为了评价所提出的光谱表征算法的性能，搭建光谱共焦实验系统，其中宽光谱光源选用Thorlabs 光纤耦合式白光LED 及LEDD1B 驱动器；色散系统选用欧姆龙ZW-S5030 光纤同轴位移传感器，零位工作距离设定为该探头的测定中心距离30mm，色散范围为±2mm；光谱仪选用分辨率为0.5nm 的CCS100 小型光谱仪；并采用TH200R5S2A 多模光纤耦合器连接光源、色散系统与光谱仪，将宽谱白光传输至色散探头并接收样品表面反射的色散光。

3.1 不同数据处理模型的比较

实验系统中将反射镜固定于连胜LSSP-13XVR 五轴精密位移台上，首先将反射镜移动至色散探头的零点工作位置，利用光谱仪对光谱数据进行采集。如图3（a）所示为光谱共焦系统在零点工作状态的原始谱图。为了避免无用的光谱信号对数据处理的影响，对原始的光谱数据进行去噪处理与强度归一化处理后，仅截取半高全宽谱段范围内的光谱作为峰值提取的样本数据。然后采用传统的最值法、质心法、高斯拟合法以及所提出的GRNN 方法对处理后的光谱数据进行进一步处理，将提取到的峰值波长与通过欧姆龙光纤同轴位移传感器获取的色散探头零点工作位置的标定波长573.3 nm 进行比较，与标定波长的偏差值即为峰值波长的提取误差。

图3 色散探头零点工作状态的原始谱图曲线Fig.3 Original spectrum curve of zero working state of dispersion probe

如图3（b）所示为原始谱图去除背景噪声，光强归一化等操作后截取的有用光谱数据，波长范围为565～580 nm，实际采样间隔为0.1 nm，为改善由于离散采样信号引起的峰值波长提取误差，利用线性插值函数处理截取的光谱数据，通过在拟合曲线上真实像素之间插值等距虚拟像素，将数据采样间隔缩小为0.01 nm，波长波动差异将缩小到真实像素区间的十分之一，降低原始波动数据的计算权重，通过虚拟像素获得1 500个数据，通过最值法获得的峰值波长为573.4 nm，与标定波长相差0.1 nm。质心法提取的峰值波长为573.08 nm 与标定波长相差0.08 nm。图4（a）与4（b）所示分别为高斯拟合与多高斯拟合的拟合效果，多高斯拟合效果明显优于单高斯拟合函数，将拟合均方根误差（Root Mean Square Error，RMSE）从1.43×10-3缩小至1.73×10-4，信噪比从34.689 5 提升到52.574 2，拟合相关系数R2从0.455 2 增大至0.991 5，在零点位置提取到的峰值波长均为573.1 nm，与标定波长573.3 nm 相差0.2 nm。

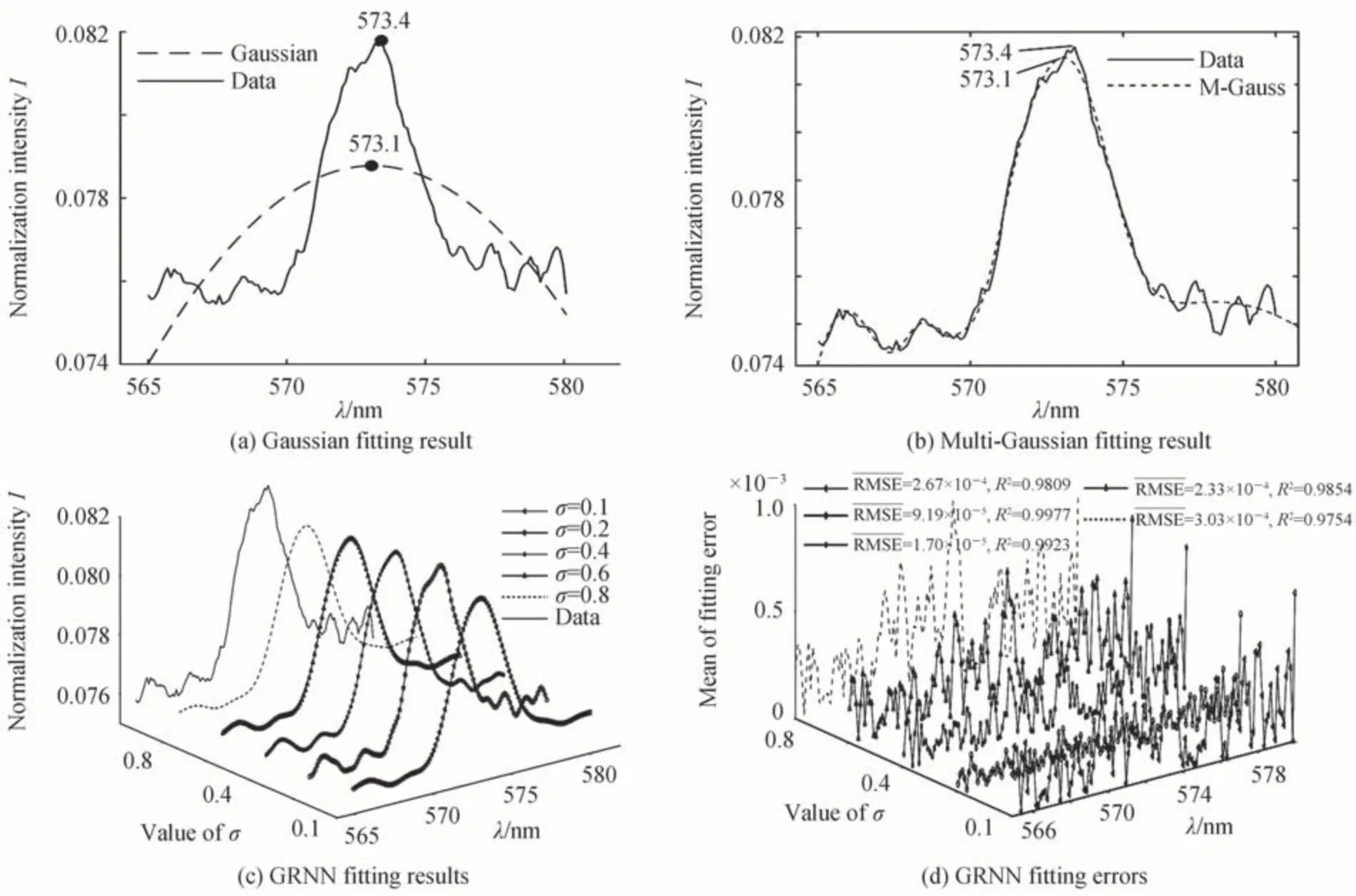
图4 色散探头零点工作状态的谱图曲线拟合效果对比Fig.4 Comparison of fitting effect of spectrum curve in zero working state of dispersion probe

在GRNN 模型的实验中，按80%、20%的比例将训练样本随机分为训练集和测试集，并使用5 重交叉验证，训练光滑因子分别为0.1，0.2，0.4，0.6，0.8 的GRNN 模型，将交叉验证得到的均方根误差的平均值作为算法的性能评价指标。如图4（c）与4（d）分别为不同光滑因子的GRNN 模型对光谱响应数据的拟合效果与其拟合误差。光滑因子分别为0.1，0.2，0.4，0.6，0.8 的GRNN 模型均低于高斯拟合模型，拟合信噪比分别为51.2465，58.4994，53.1813，50.4090，48.1358，高于高斯拟合模型，拟合系数R2分别为0.9809，0.9977，0.9923，0.9854，0.9754，大于高斯拟合模型，因此GRNN 模型的拟合效果整体优于高斯拟合。而多高斯拟合效果介于光滑因子为0.4 与0.6 的GRNN 模型之间，拟合性能劣于光滑因子为0.2 的GRNN 模型。通过比较表明，在色散探头的零点工作位置，光滑因子σ=0.2 的GRNN 模型，提取的峰值波长最准确，信噪比最高，拟合相关系数最大，拟合效果最优。

为比较不同模型在色散探头的不同工作位置的光谱表征性能，移动反射镜，令色散位置的标定波长范围为500～650 nm，间隔为10 nm，并分别利用最值法、质心法、高斯法、多高斯方法进行光谱分析，提取峰值波长与标定波长相比，得到峰值波长定位的偏差值，并对所有标定点位置的峰值波长偏差值取均值。并且令GRNN 模型的光滑因子在0.1 到0.8 离散取值，对不同位置的峰值波长进行提取，对每个实验标定点基于交叉验证产生的峰值波长偏差值取均值后，再对所有实验标定点的峰值波长偏差均值再进行一次累加平均，与传统算法的峰值波长提取误差均值进行比较。

通过实验得到，最值法的峰值波长提取误差均值为0.14 nm，质心法为0.09 nm，高斯法为0.12 nm，多高斯拟合方法为0.07 nm。如图5所示，利用GRNN 模型进行光谱拟合时，光滑因子σ=0.2 时峰值波长提取的均值误差约为0.052 nm，优于GRNN 其他的光滑因子模型，同时优于传统算法，性能最佳。

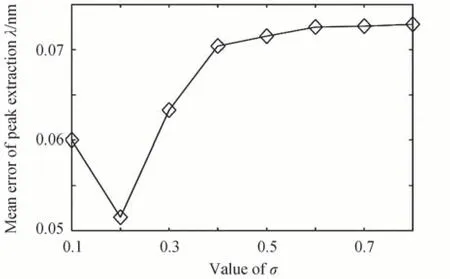
图5 Spread 取值对不同位置的峰值波长提取的影响Fig.5 Influence of spread value on peak wavelength extraction at different positions

3.2 校准实验

为比较传统算法与GRNN 模型对系统测量结果的准确性，对峰值波长与色散焦移的对应关系进行校准。在实验系统中仍然将反射镜固定于连胜LSSP-13XVR 五轴精密位移台上，在±2 mm 的测量范围内，令色散探头以0.2 mm 的步长扫描反射镜，每次实验重复五次，总共记录105 条光谱数据。参考GRNN 模型在光谱表征方面优良的性能表现，选择GRNN 模型的光滑因子σ=0.2 作为GRNN 模型数据处理方法的最佳模型，与最值法、质心法、高斯拟合、多高斯拟合法进行对比。采用这些数据处理方法对每个位置记录的五次光谱数据进行峰值提取，并对提取的峰值波长取平均值，并利用五阶线性拟合获得波长-位移的对应关系。

基于图6 的实验仿真结果，五种算法在±2 mm 的测量范围内，对色散波长与焦点位置的五阶拟合产生了相似的结果。但是GRNN 色散模型与标定点相比，色散位置的测量均方根误差约为0.01 μm，小于质心提取的均方根误差约为0.06 μm，高斯算法的均方根误差约为0.05 μm，多高斯拟合算法均方根误差约为0.03 μm，最值法均方根误差约为0.07 μm，表明GRNN 算法与传统算法相比，在约150 nm 的光谱波长范围内建立的色散模型关系是足够精确的。并且光谱共焦系统的性能由波长-位移拟合直线的斜率和相关系数决定，斜率越大表征系统测量的灵敏度越高，相关系数越大则保证系统的校准误差越小。基于GRNN 方法的波长-位移拟合直线提供了最好的拟合相关系数为0.999 9，相关系数非常接近1，表明GRNN的光谱分析结果在±2 mm 的数据范围内是高度线性的，非常适用于位移测量。

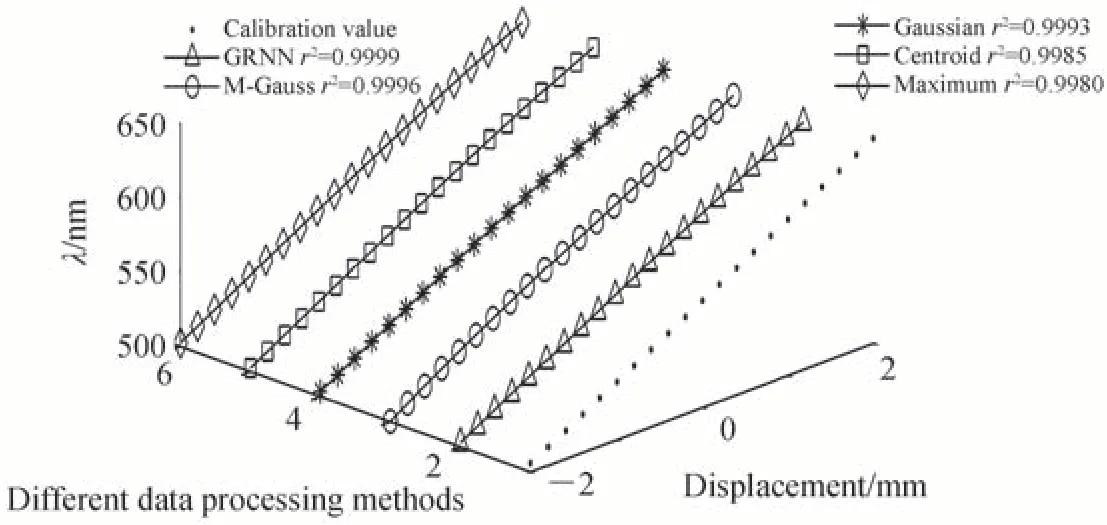
图6 不同数据处理模型的比较Fig.6 Comparison of different data processing models

3.3 分辨率和稳定性实验

为进一步分析基于GRNN 模型的光谱共焦系统分辨率，利用连胜LSSP-13XVR 五轴精密位移台移动色散探头扫描反射镜，位移间隔分别为5 μm、3 μm、2 μm 和1 μm，光谱仪的积分时间设定为0.005 s，进行了一系列实验。

如图7（a）所示，5 μm 的位置差可以通过该系统容易地辨别。当步长缩短到3 μm 时，系统仍然平稳运行（图7（b））。如果步长缩短至2 μm，波长-位移曲线的趋势保持正确，但线条的形状变为锯齿形，表明系统开始失去识别能力（图7（c））。当步长缩短到1 μm 时，由于光谱仪分辨率的限制，系统失去了测量能力。从分辨率测试的结果可以推断，基于GRNN 模型的光谱共焦系统的分辨率接近2 μm，可以识别远小于0.5 nm 的波长间隙，表明光谱数据的GRNN 分析过程有助于突破光谱仪分辨率的限制，提高系统测量的分辨率。

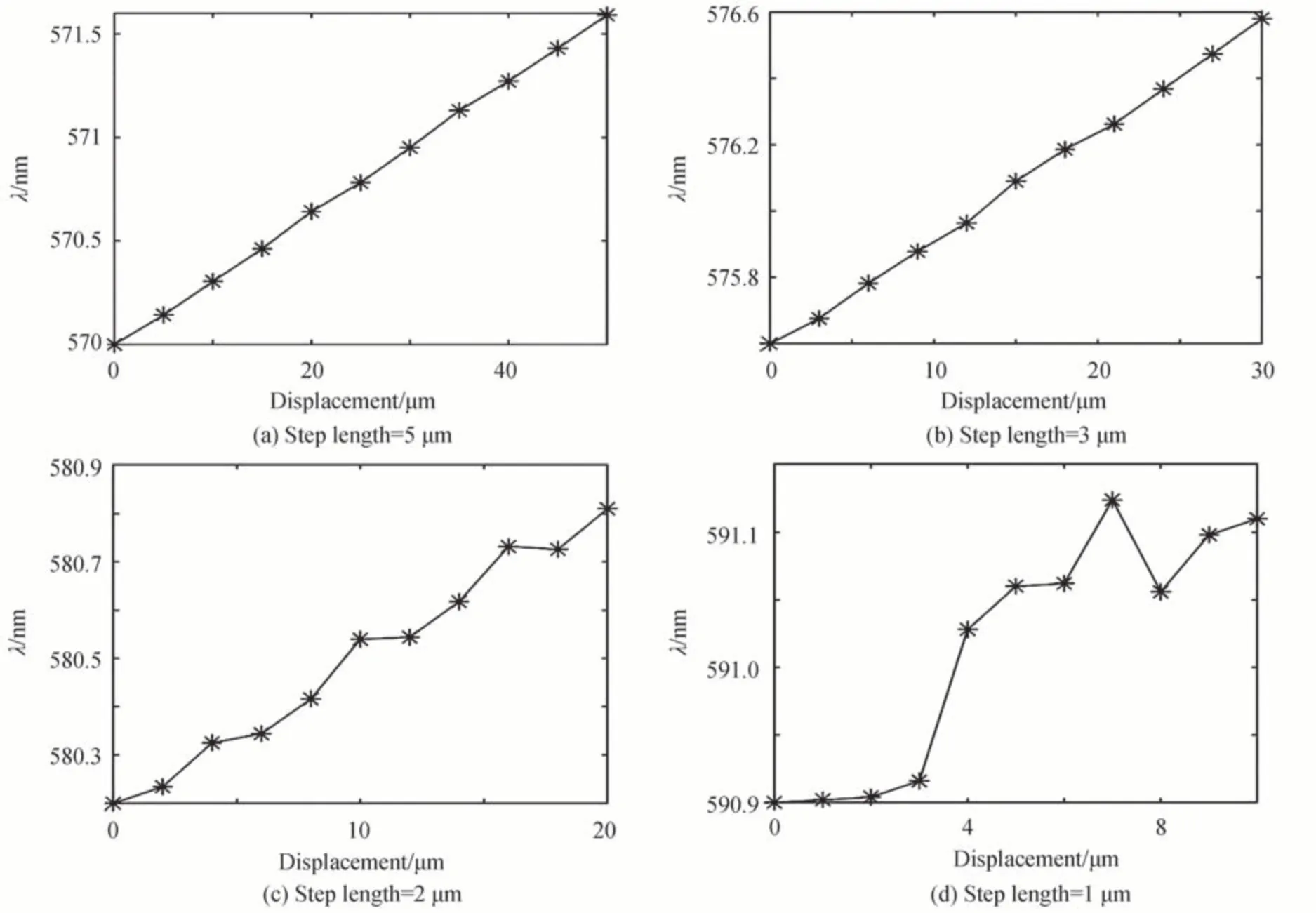
图7 不同步长下GRNN 模型的分辨率实验结果Fig.7 Experimental results of resolution of GRNN model with different step length

为了测试GRNN 模型对系统测量的稳定性，分别以10 s 与30 s 的时间间隔对距离色散镜头的零位工作点0.532 mm 位置处的单个位置的反射光谱记录20 次。

在短期测试中，测量波长的标准偏差为0.07 nm，对应于位移为2 μm 的位移偏差（图8（a））。在长期测试中，测量波长的标准偏差约为0.12 nm，对应于2.9 μm 的位移偏差（图8（b））。该结果与分辨率实验中得出的分辨率不小于2 μm 结论相一致。

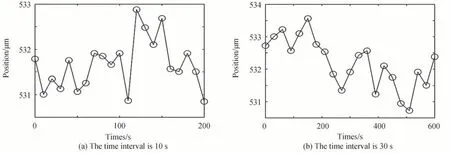
图8 GRNN 模型不同时间间隔的稳定性实验结果Fig.8 Experimental results of stability of GRNN model at different time intervals

3.4 误差分析

综合分析仍然存在的系统测量误差，产生的原因可能包括：1）本研究中的所有实验基于运动平台对反射镜的机械扫描，容易由机械移动引起一定的测量误差；2）本实验选用的光谱仪分辨率为0.5 nm，选用分辨率更高的光谱仪能够进一步提高测量准确性；3）使用光谱仪检测并记录实验数据的模数转换过程中，可能由于数据处理产生一定的误差。一般来说，一定限度内较长的积分时间和更多平均时间有助于减少误差，但也会降低时间分辨率；4）由于系统测量的部分光路是裸露于空气中的，特别是产生目标色差的光轴附近，因此测量结果还可能受到空气湍流噪声和环境变化的影响。如果将整个系统封装起来，避免空气湍流、环境光以及温度等变化的影响，可以实现更高的测量稳定性和精度。

4 结论

本文基于光谱共焦技术实现精密测量过程中峰值波长的提取对测量结果的影响，利用GRNN 模型非线性映射能力强的优点，提出利用GRNN 模型替代传统的最值法、质心法、高斯拟合等方法实现光谱分析。实验结果表明GRNN 模型的光谱表征能力优于传统算法，峰值波长的提取更加准确，进而五阶线性拟合出的色散焦移拟合系数为0.999 9，分辨率接近2 μm，RMSE 约为0.01 μm。该方法提高了光谱响应的信噪比，有效地抑制了由于峰值波长提取而引起的色散模型波动，提高了光谱共焦系统测量的分辨率与稳定性。