用于彩色光照粒子图像测速的粒子场模拟成像

单良，施飞杨，洪波，王道档，熊俊哲，孔明

（1 中国计量大学信息工程学院浙江省电磁波信息技术与计量检测重点实验室，杭州310018）

（2 中国计量大学计量测试工程学院，杭州310018）

0 引言

流体在自然界和工程领域中非常普遍。燃烧的火焰、大气中的湍流［1］和海洋的涡旋都是自然界中典型流场现象。流体力学和空气动力学等工程领域的研究和流体的测量息息相关，掌握流体的具体运动情况是流体力学深入研究的前提条件，测量和分析流体的运动状态是流体领域的关键问题［2］。粒子图像测速法发展于19世纪80年代，集现代材料、数字成像、激光技术和图像分析等领域的发展成果于一体，是一种瞬态、多点、无接触式的流体力学测速方法，可以精确地测量平面内的瞬态流场。在不干扰流体运动的情况下，为流体运动的定性描述以及定量研究提供相对理想的数据基础［3］。

基于彩色光照的粒子图像测速法（Particle Image Velocimetry，PIV）是结合了彩色三维重建和三维光流图像算法的一种三维粒子图像测速算法。用颜色编码粒子在三维流体中的深度位置，结合粒子在图像上的二维位置信息，用单个彩色相机就能够重建流场的三维速度矢量场。而层析PIV 获得三维速度信息需要使用多个相机从不同角度对流场中的粒子进行拍摄，在实际层析PIV 的实验装置搭建时，多个相机的摆放和拍摄角度受空间限制较大、而且调试复杂，在实际测量流体时具有较大的限制［4］。与之相比，彩色PIV 的实验装置更加简单，易于搭建，测量的局限性更小，更能适应不同的真实测量环境［5］。对于彩色粒子图像测速算法，早在1992年，SMALLWOOD G J 等［6］为了研究燃烧现象中的复杂流场，开发了一种双色PIV 降低了二维速度重建时对数据处理的要求。2003年，DEPONTE S［7］等对一种三色粒子图像测速法对循环流进行了研究，通过三种颜色的闪光在两种不同的时间间隔下照射流场，在同一图像上应用互相关算法可以获得三个速度场，即使在速度差异很大的流场中也能得到准确的测量结果。2017年，XIONG J H 等提出了RainbowPIV，用颜色来编码粒子的深度，建立图像形成模型来重建粒子分布场，并用结合图像形成模型和物理约束的三维光流算法估计三维速度矢量场。用单个RGB 相机就能还原粒子的三维速度场，并在后续研究中和层析PIV 进行了对比，采用同步测量装置同时对涡环发生器中的流场进行了测量，验证了RainbowPIV的正确性。粒子图像测速算法在不同类型的流场表现不同，流场中的粒子粒径大小、粒子密度等因素也会对PIV 的重建效果有所影响。为了研究不同的粒子特性、流场类型等因素对彩色PIV 的影响，进一步提升彩色PIV 算法的性能和重建精度，需要大量的数据集进行分析重建。涡流、射流等复杂流体的实验装置搭建难度高，也难以得到准确的速度场真值。因此需要通过计算机模拟不同实验条件下的粒子场来支撑彩色PIV 的研究。

本文介绍了一种结合相机针孔模型和点扩散函数的成像模型，模拟彩色光照下流场中示踪粒子的成像结果。从彩色PIV 的实验要求和物理假设出发，利用计算机进行数值计算，结合粒子成像模型和流体运动模型得到模拟流场中的示踪粒子彩色图像。采用RainbowPIV 对模拟的彩色粒子图像进行三维重建，对重建结果进行误差分析，验证模拟图像的正确性。

1 粒子成像原理

在基于彩色光照的粒子图像测速算法中，示踪粒子的成像是彩色PIV 研究的基础。只有得到准确的粒子成像的图片才能得到良好的粒子分布场的重建结果。在示踪粒子成像时，示踪粒子的密度、粒径、表面反射率等特性对成像均有一定的影响［8］。其中示踪粒子的粒径是影响粒子的流动跟随性、反射率以及成像可见性的主要因素［9］。粒子的粒径越小，粒子的流动跟随性就越好，测得的粒子的速度与流体的真实速度更加接近，但是相应的粒子的成像可见性就越小，因此需要根据示踪粒子的特性合理选择示踪粒子保证成像结果的质量［10］。同时，照明系统也是影响粒子成像质量的重要因素。传统的二维PIV 的照明系统由激光光源和柱透镜组成，得到垂直于相机视线的片状光来照亮流场中的示踪粒子。通过观察跟踪照明平面中移动的粒子来获得当前片状光照亮的2D 切片上的速度场的两个速度分量［11］。三维PIV 需要获得三个方向上的速度分量，片状光的照明系统无法满足三维PIV 的测量要求，需要用体光源来照亮待测流场［12］。

彩色PIV 模拟实验装置图如图1所示，由白色光源、准直透镜和线性滤波片（波长在可见光范围内线性变化）、样品池以及CCD 相机组成。其中光源、准直透镜和滤波片构成彩色照明系统，样品池用于盛放流体和示踪粒子，CCD 相机用于采集粒子图像。工作原理为非相干光源发出白色的扩散光束，经过准直透镜得到平行的白色光束后，通过线性滤波片对光束进行滤波得到彩色的体积光，照亮样品池中的示踪粒子并用可见光的波长来编码粒子的深度。采用CCD 相机来采集粒子的图像，将流场中的粒子建模为对应深度变化的不同波长的窄带点光源，然后通过针孔模型分析光路得到粒子点光源中心在CCD 传感器平面上的位置，进而得到粒子场在CCD 传感器上的光谱分布。

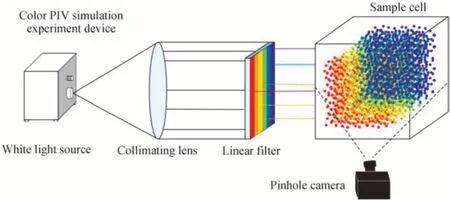
图1 彩色PIV 模拟实验装置Fig.1 Color PIV simulation experimental device

2 粒子模拟仿真

2.1 彩色照明光路模拟

彩色照明系统是模拟粒子场成像的关键一环。要保证成像的清晰程度，提高信噪比，需要入射到流场中的体积光的强度足够大。为了提高彩色PIV 重建时深度方向上的精度，需要保证不同深度的粒子在CCD上的成像效果相同，因此在满足入射体积光强度大小要求的同时还要保证照明范围内光强均匀分布。与层析PIV 的单色体积光不同，为了得到波长随深度变化的彩色体积光，需要采用非相干宽谱光源来代替激光光源。搭配线性可变滤波器对非相干宽谱光源发射的白色光束进行滤波，最终得到波长随深度线性变化且光强均匀的彩色体积光。照明系统的光路分析在TracePro 软件中进行模拟仿真。

仿真光源数据的选择参考THORLABS 的自由空间宽带光源SLS301，白光光束直径为50 mm，波长范围为360～3 800 nm，输出功率为1.6 W。线性可变滤波器仿真时由20 个波长在450 nm～880 nm 内递增的厚度为1 mm 的滤波片组成，组合后的线性可变滤波器大小为45.7 mm×32.5 mm。因为光束直径较大，多余的杂光会影响照明效果，因此可以设置一个光阑来过滤杂光，增强成像的效果。在TracePro 中进行彩色照明光路的模拟仿真，添加一个大小和线性可变滤波器一致的传感器来接受光线信息，计算每个点的吸收光通量的大小。经过光线追迹可以得到每个空间点的光通量的大小。图2 为当光源发出光线数量为17 867条时传感器上得到的辐照度分析图，可以看到彩色体积光的不同深度的光通量大小基本一致，满足彩色PIV中的彩色体积光的实验要求。

图2 传感器的辐照度分析图Fig.2 Irradiance analysis of sensor

2.2 相机针孔成像模型

在彩色照明系统得到波长随深度线性变化的彩色体积光之后，用获得的彩色体积光照射流体中的粒子，流体中不同深度的粒子反射对应波长的粒子的光，不同深度的粒子建模为不同波长的窄带点光源。为了得到每个粒子成像在CCD 传感器平面上的准确位置，得到粒子场在CCD 传感器上的光谱分布，需要建立相机针孔模型［13］对粒子成像的光路进行分析模拟。

首先建立对应坐标系：1）像素坐标系——以像素为单位的CCD 图像平面坐标系，坐标轴原点O0如图3所示，像素坐标系(u，v)表示该像素在图像矩阵中的位置；2）图像坐标系——以物理单位建立的CCD 图像平面坐标系，坐标轴原点O1为相机的光轴和图像平面相交的点，图像坐标系的坐标轴x轴和y轴分别平行于像素坐标系的u轴和v轴；3）相机坐标系——坐标轴原点OC为相机的光心，OC和O1之间的距离为相机的焦距f，坐标轴XC轴和YC轴分别与图像坐标系x轴和y轴平行，ZC轴为相机的光轴；4）世界坐标系——由于相机和粒子在自然环境中的位置是不确定的，因此除上述坐标轴外还需要设置世界坐标系，用(XW，YW，ZW)来表示在自然环境中的位置。如图3所示。

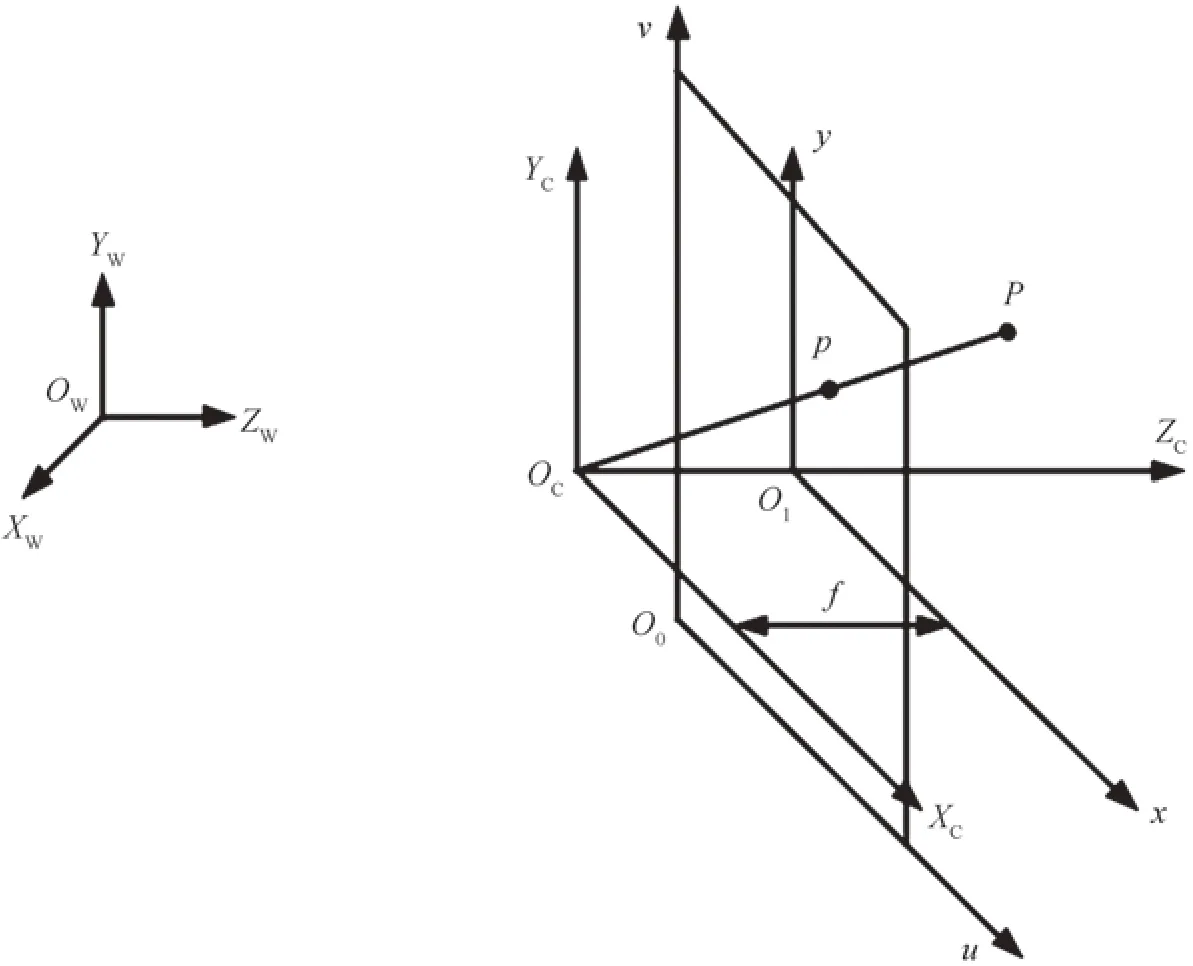
图3 针孔相机模型Fig.3 Pinhole camera model

当彩色的体积光照亮流场中的粒子P时，由于采用的是非相干光源，可以将P视为点光源。P的世界坐标系为(XP，YP，ZP)，ZP决定了粒子P发出的光线的波长，同时在忽略相机的畸变因素下，可以将相机的成像模型看作是一个针孔模型，粒子成像中心在图像平面上的位置p(x，y)也就是相机光心OC和P的连线和成像平面的交点。根据相机的焦距f和粒子世界坐标系的深度ZP可以计算得到投影点p即粒子在相机拍摄图像中的点的坐标［14］

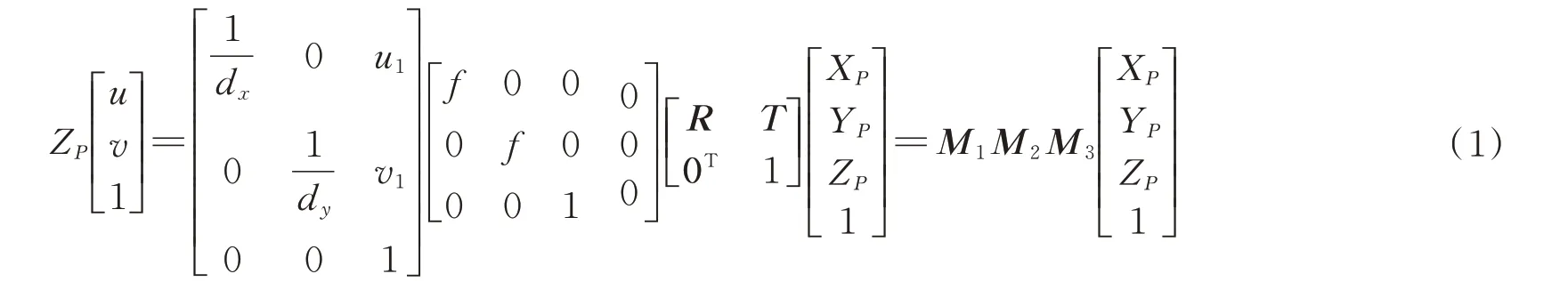
式中，M1是一个3×3 的从图像坐标到像素坐标的转换矩阵，M2为3×4 的相机坐标到图像坐标的转换矩阵。M3为4×4 的从世界坐标到相机坐标的转换矩阵，R为3×3 的旋转矩阵，T为1×3 的平移向量，R和T的值由相机在世界坐标系中的位置决定。

2.3 点扩散函数

在上述相机针孔模型中把不同深度的粒子建模为波长不同的窄带点光源，一个理想的点光源通过针孔成像模型成像后，该点光源的成像是一个被拓展的模糊的面源像，忽略噪声的干扰，该点源形成的面源像就是点扩散函数（Point Spread Function，PSF），成像系统的PSF 是空间分辨率和密度分辨率的决定因素［15］。

粒子入射到图像平面上的PSF 可以通过两个步骤求解，首先需要对粒子的成像直径进行求解，根据ADRIAN R 和YAO C S［16］的研究，粒子的面源像直径即成像直径de。成像直径de可以通过粒子的真实直径dp和粒子的散射光线经过相机透镜后产生衍射在图像平面上形成的艾里斑直径ds计算得到

式中，

由式（3）可知艾里斑直径与成像模型的放大率M、粒子反射光线的波长λ以及数值孔径f#相关。由于采用的光源为彩色体积光，因此不同深度的粒子反射的光的波长不同，粒子在图像平面上的艾里斑直径ds也不同。为了使不同深度的粒子在图像平面上的成像直径de一致，需要粒子的真实直径dp足够大，当粒子的真实直径足够大时，照射粒子的光的波长对粒子成像直径的影响可以忽略不计。

因此，选用直径为100 μm 的粒子作为仿真对象。当dp=100 μm，M=1，f#=8，取彩色体积光的波长范围中间值作为λ的计算值，λ=665 nm。代入公式计算可得粒子的成像直径de=103.315 μm，由于采用的CCD 相机的单位像素的尺寸大小为21 μm×21 μm。因此可以将粒子在图像平面上的成像离散化，用5×5的PSF 来表示粒子在图像平面上的成像。因为粒子的光强分布应满足二维高斯分布，离散化得到的图像归一化强度矩阵中的值通过粒子光强分布权函数得到

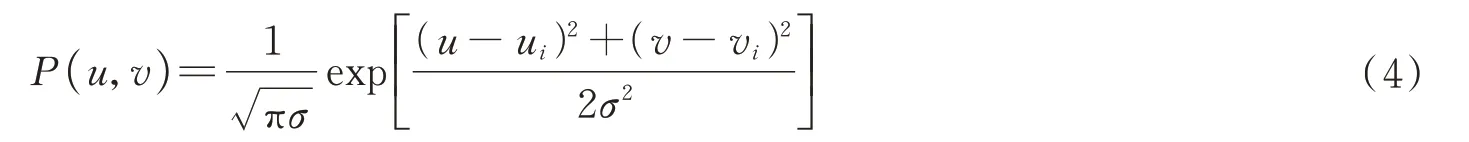
式中，(u，v)为像素平面的位置，(ui，vi)是流体中某一粒子投影到像素平面的位置，σ为高斯函数的方差，又称平滑因子，与粒子成像的直径相关。

由彩色照明模拟光路的仿真结果可得，不同深度的粒子受到波长不同但是强度相同的光线照射，根据归一化强度矩阵和光的颜色得到的对应不同深度的PSF 如图4所示。

图4 不同深度下的粒子的PSF 图Fig.4 PSF of particles at different depths

3 粒子图像分析

3.1 模拟粒子图像

3.1.1 图像形成模型

在非相干成像系统中，图像形成过程中的图像强度在线性系统理论描述中是线性的。生成的图像可以视为独立个体成像对象的总和。根据光学非相干成像系统的线性特性，物体在图像计算时可以用二维脉冲函数的加权和来表示物体平面场。这些脉冲函数的图像即PSF 能反映物体平面中一点在图像平面中扩散形成的区域，图像平面可以用PSF 的加权和来计算。当物体被离散化成为多个不同强度的离散点时，物体的成像可以用每个点的PSF 之和来模拟。由于彩色照明系统中采用的是非相干光，因此可以将光学系统的成像过程建模为一组PSF，粒子的成像可以由粒子在图像平面上的光强分布和PSF 的卷积和来模拟，如式5所示。

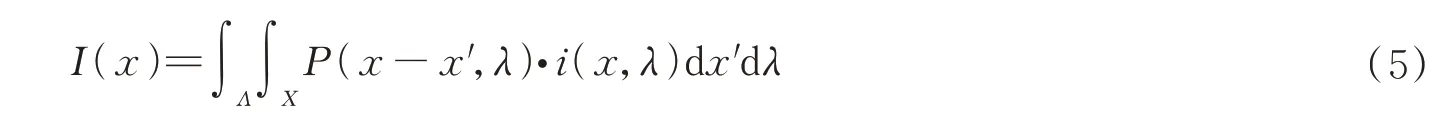
式中，λ为在彩色体积光中某一深度的粒子反射的光的波长，I(x)为相机拍摄的粒子彩色模拟图像，P(x，λ)为不同波长对应的光学系统成像的点扩散函数，i(x，λ)为粒子入射到传感器上的光谱分布。

在MATLAB 中对彩色体积光照射中的流场的粒子成像光学过程进行仿真模拟，通过相机的针孔模型得到粒子场在相机传感器上的光谱分布，与对应的PSF 函数相卷积可以生成CCD 相机拍摄的彩色粒子模拟图像。

3.1.2 模拟粒子图像的粒子分布场重建

为了验证模拟粒子图像的正确性，在72 pixel×120 pixel×20 pixel 的三维空间内随机生成50 个粒子，并记录这50 个粒子的三维坐标作为真实值。在焦距为25mm 的条件下，根据建立的针孔模型得到粒子场在CCD 上的光谱分布。和上文得到的PSF 相卷积得到模拟的彩色粒子图像如图5。

图5 随机生成的50 个粒子模拟图像Fig.5 Simulation image of 50 particles randomly generated

采用XIONG J H 等在2017年提出的RainbowPIV 对模拟图片进行分析重建，结合粒子成像模型和粒子稀疏性以及运动一致性的正则项得到关于粒子在三维空间分布的最小化问题，并采用交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）求解得到模拟图像对应的三维粒子分布场。重建结果和真实值进行对比如图6所示，重建得到的50 个粒子的三维坐标和真实值之间的误差基本在5%之内。

图6 重建结果与真实值对比图Fig.6 Comparison between reconstruction results and real values

3.2 模拟流体速度场

3.2.1 流体运动模型

彩色PIV 重建流体三维速度场需要对间隔时间t拍摄的两幅粒子图像进行对比分析。单个图像只能得到当前时刻的流体中的粒子分布场，无法得到流体的速度场。因此需要建立流体运动模型对流体速度进行模拟。本文采用朗肯涡流（Rankine Vortex）［17］来模拟流体的运动，并结合图像形成模型来得到重建三维速度场所需的仿真数据集。

朗肯涡流是以物理学家RANKINE W J M 的名字命名的一种流体模型，是真实飓风和龙卷风研究的理论依据。朗肯涡流模型是一种内部区域为刚性核心内旋涡流，外部区域为无旋旋涡的圆形流。朗肯涡流是具有径向对称的一种流体流动，在圆柱坐标系(r，θ，z)中以z坐标轴为对称轴，流体的速度公式如式（6）和（7）。

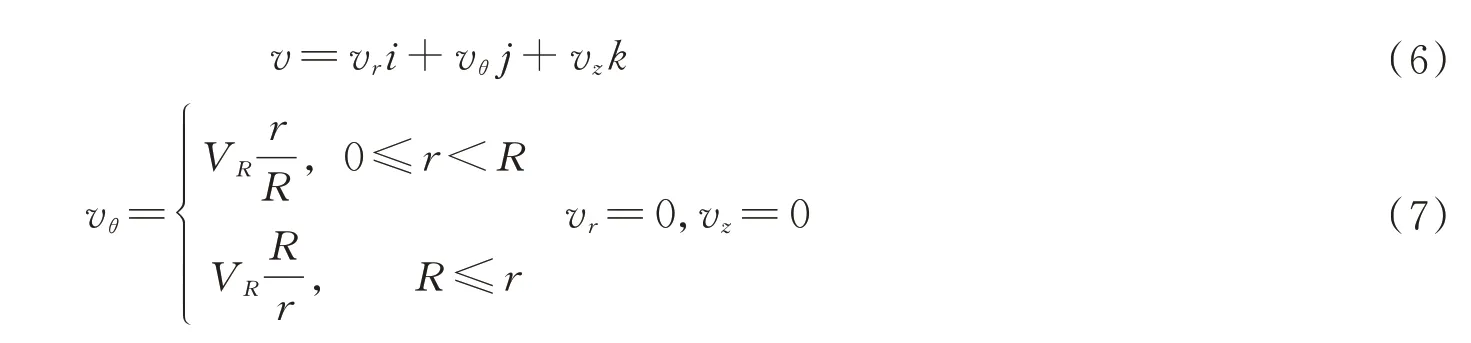
式中，i、j、k分别为与r轴、θ轴、z轴平行的单位向量。vr、vθ、vz为对应坐标轴方向的速度大小。VR为流体的最大速度，r为离刚性旋转核心的距离，R为刚性核心漩涡的半径。在径向距离r＜R时流场是一个具有刚性旋转核心的自由漩涡，速度随r线性变化，在r=R时速度为最大值；R≤r时流场为自由涡流，速度随着径向距离的增大而衰减，与真实飓风的物理特性相一致。

3.2.2 模拟粒子图像的粒子速度矢量场重建

通过朗肯涡流模型可以对粒子的运动趋势进行预测，与粒子成像模型结合可以得到重建流体三维速度矢量场所需要的模拟图像对。由于重建速度场对粒子的密度具有一定的要求，因此在72 pixel×120 pixel×20 pixel 的三维空间内随机生成300 个粒子。根据粒子成像模型对t1时刻流体的粒子图像进行模拟，结果如图7（a）。在三维空间中生成一个单漩涡中心的朗肯涡流，设定刚性漩涡中心的坐标为［60，36］，刚性核心漩涡的半径为30 pixel，流体最大速度为5 pixel/s。将t1时刻的模拟粒子图像中的每个粒子根据粒子在三维空间中的位置获得对应的速度，并进行1 s 的位移得到t2时刻的模拟粒子图像如图7（b）。

图7 朗肯涡流下的模拟粒子图像Fig.7 Simulated particle images under Rankine vortex

根据涡流公式得到三维模拟速度场如图8（a）所示，用彩虹PIV 对仿真图像对进行分析重建，得到粒子的三维分布场后，将NavierStokes 方程中制定的物理性质和传统的Horn-Schunck 光流方程相结合构建关于三维速度矢量场的最小化问题，用ADMM 算法求解得到120×72×20 的三维矩阵，即重建的三维速度矢量场。为了较好的比较原始流场和重建结果的物理性质，将120×72×20 的三维矩阵线性插值后抽样得到12×7×10 的三维矩阵，三维模拟速度场和三维重建速度矢量场如图8（b）。

图8 三维速度矢量场的模拟和重建Fig.8 Simulation and reconstruction of the three-dimensional velocity vector field

将重建结果和真实值进行对比，用平均终点误差（Average End Point Error，AEPE）和平均角度误差（Average Angle Error，AAE）来评价重建速度场结果分别在速度大小和速度方向上的准确性［18］，AEPE、AAE 的计算公式为

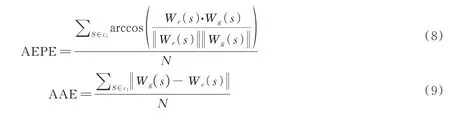
式中，s为图像坐标，Wr(s)和Wg(s)分别表示重建的速度与流体速度真值，c1为图像单点位置集合，N为c1的大小。根据计算得AAE 为13.744 7°，证明采用RainbowPIV 对模拟粒子图像进行重建时能相对准确的重建流体的运动趋势。在重建流体速度场大小方面，在最大速度为5 pixel/s 的单漩涡中心朗肯涡流的仿真条件下，AEPE 的大小为0.948 5 pixel。XIONG J H 在2017年采用RainbowPIV 对旋转轴与光轴正交的漩涡进行了重建，重建结果AAE 为13.65°、AEPE 为0.73 pixel［5］。本文对朗肯涡流模型和粒子成像模型相结合生成的仿真图像进行重建后的结果与参考文献中的相接近。将重建三维速度矢量场图8（b）和模拟三维速度场图8（a）进行对比，光流法重建速度矢量场无法完全还原模拟速度场，尤其是在边界部分容易产生误差，所以重建结果和模拟流场存在差异。但是重建结果很好地还原了单漩涡中心的速度特性，能较好地反应仿真流场的物理性质。验证了模拟粒子图像的正确性，可以用模拟图像来进行彩色PIV 的仿真性能分析，为彩色PIV 的研究提供支撑。

模拟图像中包含的粒子数量以及粒子的速度也会对重建的结果产生影响。在72 pixel×120 pixel×20 pixel 的三维空间内随机生成100、200、300、400、500 个粒子，根据粒子成像模型得到对应的粒子模拟图像。结合三维空间中生成的最大速度分别为1 pixel/s、2 pixel/s、3 pixel/s、4 pixel/s、5 pixel/s，刚性漩涡中心的坐标为［60，36］，半径为30 pixel 的五个单漩涡中心的朗肯涡流场得到25 个模拟粒子图像对。并采用RainbowPIV 进行分析重建得到对应的AEPE 和AAE 的值绘制了图9。

图9 不同速度不同粒子数量对重建误差的影响Fig.9 Influence of different velocity and particle number on reconstruction error

从图9 分析可得，在粒子数量相同时，粒子速度越大AEPE 越大，而AAE 随着速度的增大而减小，这是因为在同样的速度误差情况下，速度越小，引起速度方向上的改变就越大。在涡流最大速度相同时，粒子数量越多，AEPE 的值越小。粒子数量为200 时的AEPE 明显小于粒子数量为100 时的值，而粒子数量为300、400 和500 时的AEPE 相对比较接近，这是因为图中的粒子越多，进行三维重建时的信息就越多，三维重建的结果越精准。而当图中的粒子数量足够三维重建所需的信息量时，提升粒子数量难以进一步降低AEPE。粒子数量对AAE 的影响较小，在粒子数量差距较大的情况下，粒子数量越多重建结果越好。

4 结论

本文综合彩色PIV 的实验条件和实际的涡流参数，建立了一个针对彩色PIV 的彩色粒子图像模拟系统。彩色粒子图像模拟由三部分组成，彩色照明系统模拟提供了不同深度光强一致的彩色体积光，通过相机针孔模型得到在彩色体积光照射下的粒子场在CCD 传感器上的光谱分布，粒子场的光谱分布与PSF 相卷积得到彩色粒子模拟图像，结合朗肯涡流模型生成的三维流体速度场可以得到彩色仿真粒子模拟图像对。采用彩虹PIV 对图像对进行分析重建，将重建得到的三维粒子分布和三维速度矢量场与仿真数据进行对比，三维粒子分布中的粒子位置与真实值之间的误差在5%之内，重建的三维速度矢量场的AAE 为13.744 7°，AEPE 为0.948 5 pixel，并且准确地重建了仿真流体的物理性质，验证了模拟粒子成像的准确性。模拟了不同粒子数量和不同速度大小的朗肯涡流下的彩色粒子图像对并进行重建分析。粒子数量相同时，AEPE 随着粒子的速度增大而增大，而AAE 则相反；粒子速度相同时，AEPE 随着粒子数量的增大而减小，对AAE 的影响不大。彩色粒子图像模拟系统可以根据真实实验条件，通过仿真系统控制粒径大小以及粒子密度模拟彩色粒子图像，联合不同的流体速度场可以模拟粒子在不同流体中的运动。本文研究对现有的彩色PIV 的改进具有支撑作用。