脉冲射线源三维中子成像重建算法研究

盛亮，张艳红，高建鹏，李阳，段宝军，黑东炜

（1 西北核技术研究所强脉冲辐射环境模拟与效应国家重点实验室，西安710024）

（2 清华大学工程物理系，北京100084）

0 引言

近二十年来，激光、Z 箍缩驱动聚变点火技术取得了长足进步［1-2］，氘氚燃烧区的空间分布反映了所有点火物理过程的最终状态，精确诊断燃烧区空间结构对于改进压缩对称性技术措施、校验物理模型、评估点火成败等具有重要意义，不同能量的中子图像能够直接给出燃烧区以及周围物质在高压缩比条件下的空间分布，因此中子成像技术是研究脉冲射线源性能的核心技术［3-5］。吕敏院士、王奎禄研究员等在20世纪80年代建立了基于厚针孔、射线图像转换屏、选通型像增强器、高速图像记录等关键技术的中子、伽马成像系统，这些基本技术思路几十年来没有发生根本性的变化，但针对测量对象特征的不同进行了一些重要技术改进，如针对低强度脉冲中子源，开展了半影孔、环形孔成像与图像复原技术研究［6-8］，发展建立了多分幅相机、条纹相机、光纤-光电倍增管阵列等三种不同的时空分布信息记录系统［9，10］。单光轴中子成像获得的二维图像是辐射区域中子的沿着特定方向线积分投影，无法直接反映氘氚燃烧区域内部的三维空间分布，如氘氚燃烧区体积等重要物理参数需要根据旋转对称假设给出。最近在高能量密度物理研究领域，数值模拟程序由二维向三维发展，美国国家点火装置（National Ignition Fusion，NIF）团队的研究结果表明，三维模拟程序计算的中子产额与实验结果最为接近，三维程序给出的燃烧区分布需要直接的实验结果验证［11］。借鉴计算机层析成像思想，通过多角度成像的方式可以给出氘氚区三维分布信息，但由于脉冲射线源一般具有自辐射强、持续时间短、射线强度变化范围大等特点，这些特点使得不同光轴之间像素级精确匹配、高精度时间关联、相机灵敏度差异校正等存在较大困难，一般建立的光轴数量非常有限（≤5），如美国国家点火装置上历经十余年，完成了三条中子成像光轴建设［12］。这种基于非常有限光轴中子图像重建三维空间分布是一件极具挑战性的工作，有解空间大、存在伪影、无法保持边缘特征的问题。中国工程物理研究院江少恩等在1997年进行了ICF 聚变等离子体的X 射线三维成像技术探索，建立了基于代数重建（Algebraic Reconstruction Technique，ART）的三维图像复原算法［13］；美国VOLEGOV P L 等建立了最大期望（Expectation Maximization，EM）算法图像重建方法［14］，以及三维中子图像球谐函数分解（Spherical Harmonic Decomposion，SHD）、柱谐函数分解重建方法（Cylindrical Harmonic Deomposition，CHD）［15-16］，这种函数分解解析方法具有重建速度快、重建结果在某些限定条件下解唯一确定的优点，但其表达能力受投影角度数量的限制较大。

本文以辐射源强度空间分布为高斯函数的椭球源为研究对象，分别介绍并实现了球谐函数分解和EM迭代两种三维图像重建算法。与NIF 团队重建算法设计思路不同，根据惯性约束聚变靶燃烧区结构具有一定球对称性这一物理特点，设计了一种将球谐函数分解与EM 迭代相结合的重建算法。该方法首先以球谐函数分解对辐射源进行三维重建，然后将其重建结果作为EM 算法的初值进行迭代重建，其最终重建结果可以看作是EM 迭代算法在球谐函数分解重建结果约束下寻找到的最优解。

1 球谐函数分解三维图像重建算法

椭球脉冲射线源及x=0（短轴中心位置）处切片图如图2（a）、（b）所示，本文给出的所有切片图都为同一位置。在球谐函数分解解析求解的过程中，为了减少积分投影图像中高频噪声对结果的影响，在积分投影图像的频域中增加了低通高斯滤波器，重建图像及切片图如图2（c）、（d）所示。为了验证噪声对球谐函数分解解析方法重建结果的影响，对椭球源的积分投影图像添加两种水平的高斯噪声，噪声的标准差分别为积分投影图像最大值的2%和5%，对于噪声投影图像重建结果分别如图2（e）、（f）和图2（g）、（h）所示。通过与无噪声重建结果的切片图比较可以看到，在有噪声的情况下，解析方法重建结果中心部分产生了较大畸变，而边缘部分的重建伪影部分受噪声影响不大。

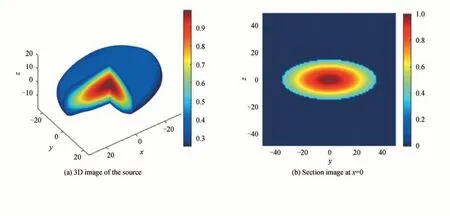
图2 球谐函数分解三维图像重建结果Fig.2 The three-dimensional image reconstructed results by spherical harmonic decomposition

无噪声重建结果的积分投影图像与理想的椭球源积分投影图像（149°，307°）的差值|Δ|及Δ的一维分布直方图如图3（a）、（b）所示，其中Δ为重建投影图像与理想投影图像之间的强度差，由于大部分差值数据为Δ=0，为了更好显示差值分布，在进行直方图统计时没有将Δ=0 的结果统计在内。2%和5%噪声水平的重建结果差值及直方图分别如图3（c）、（d）和图3（e）、（f）所示。可以看到随着噪声水平的增加，非零差值的直方图分布变的更宽，理想情况下差值图像的直方图分布的最可几值在Δ=0 附近，当噪声为5%时，差值图像的直方图分布较理想情况下出现了较大偏移，高斯拟合结果给出的最可几值出现在Δ=0.38 附近。

图3 不同噪声水平下重建三维图像投影图像与理想投影图像之间的差值及其直方图Fig.3 The difference image and its histogram between the projection image of reconstructed 3D image and ideal 3D image with different noise

2 EM 迭代算法

在中子成像中，物像距远大于辐射源自身尺寸，受厚针孔视角限制，射线经过厚针孔的有效发射角度远小于1。成像系统获取的中子图像是具有三维空间结构的脉冲辐射源沿着某一方向的积分投影图像，其矩阵形式为

式中，投影数据p为M×1 的向量，源强度f为N×1 的向量，投影矩阵A为M×N的矩阵。EM 算法是一种统计类代数迭代重建方法，可用于处理投影角度少、数据不完备的问题，较ART、MART 等代数类迭代算法具有更好的重建效果。受中子成像探测数量限制和投影噪声的影响，EM 算法随着迭代次数增加，迭代噪声增强，易引起图像质量退化［20］。

EM 迭代算法的基本思想为：假设射线源放射强度f服从泊松分布，利用观测投影数据p，通过EM 迭代寻找使似然函数的期望最大化的参量f，似然函数定义为

式中，Ai是A矩阵第i行。在EM 算法中，依赖于一组完全观测数据{zij}，数据的每个元素表示探测像素i探测到第j个辐射源体素内发射的光子数，服从Poisson 分布

式中，aij是A矩阵第i行、j列元素，fj表示向量f第j列的元素值，投影数据p与观测数据z的关系为

式中，pi表示p第i行的元素值。结合式（8）和（10），目标函数为

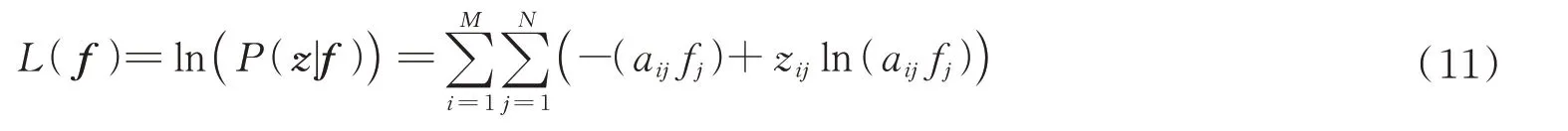
采用EM 算法分为两个步骤。

E-step：已知当前源图像fk，投影值p，观测数据的条件期望为

将式（11）的目标函数的随机变量zij用期望值代替，则有

M-step：使条件期望最大化，对目标函数求偏导。

令式（14）为零，得到经典的EM 算法迭代格式［21-22］

将每个投影方向数据作为一个子集，采用有序子集最大期望重建算法（Ordered Subset Expectation Maximization，OSEM）可以加速算法收敛速度［21-22］，本文中的算例迭代5 次即可收敛至两次迭代差别可忽略的程度。在利用EM 算法进行图像重建时易产生高频噪声，可以利用中值滤波（Median Filter，MF）、全变差最小（Total Variation Minimum，TVM）等约束方法对迭代数据进行平滑约束。文献［14］引入图像空间分布的先验信息，使用Gibbs 能量分布函数对EM 算法的迭代过程进行约束，提高了算法的噪声抑制能力。EM算法获得的是局部最优解，通常在利用EM 迭代算法时，初值设为0 或者1。如果能够将EM 算法的初值限定在一定范围内，就有可能获得与受初值约束的局部最优解。大多数对EM 算法解空间的约束依赖于投影图像数据的先验假设，如高斯先验、脉冲噪声先验、结构化先验等［23］。激光、Z 箍缩驱动惯性约束聚变研究中，为了获得更高的能量转换效率，靶丸的内爆压缩过程尽可能为对称压缩，其结构上具有一定的球对称性，基于此类物理先验信息可以帮助我们限定EM 类算法的初值，将重建结果限定在物理结构先验约束范围内，将球谐函数分解重建结果作为EM 迭代算法的初值是ICF 中子图像三维重建的一种自然选择。当然，根据重建对象的不同，EM 迭代算法的初值约束可以有不同的选择，比如辐射源具有一定柱对称性，可以利用阿贝尔变换（Abel Transform）或者文献［16］提出的柱谐函数分解重建结果作为EM 迭代算法的初值。

图4（a）～（j）为无噪声情况下图1所示5 个投影角度椭球源OSEM、MF-OSEM、球谐函数分解初值约束的MF-OSEM 算法三维图像重建结果其切片图。图4（b）中OSEM 算法重建图像给出的切片图存在较多迭代伪影，包含辐射源内部的高频噪声和边缘噪声，图4（d）中MF-OSEM 算法的结果对高频噪声进行了较好的抑制；MF-OSEM、球谐函数初值约束的MF-OSEM 重建三维图在与理想的椭球源积分投影图像（149°，307°）的差值及其直方图分别如图5（a）、（b）和图5（c）、（d）所示。从直方图中看球谐函数约束的MF-OSEM算法差值图像较MF-OSEM 算法绝对值更小，分布也更为均匀，受投影角度的影响也更小一些，直方图的强度分布都集中在Δ=0 附近。图5（e）、（f）和图5（g）、（h）分别为添加2%和5%噪声之后，球谐函数初值约束的MF-OSEM 算法重建投影图像与理想投影图像之间的差值及其直方图，与球谐函数分解结果类似，随着噪声水平的提高，差值图像的绝对值也变大，直方图分布也变的更宽，与图3（e）差值图像边缘与理想图像差别较大不同，差值图像图5（g）分布较为均匀，图5（h）的直方图高斯拟合给出的最可几值出现在Δ=0.29附近。

图1 椭球辐射源5 个角度投影Fig.1 The 5 projection views of the ellipsoidal radiation source

图4 EM 类算法三维图像重建结果Fig.4 The EM algorithm reconstructed results

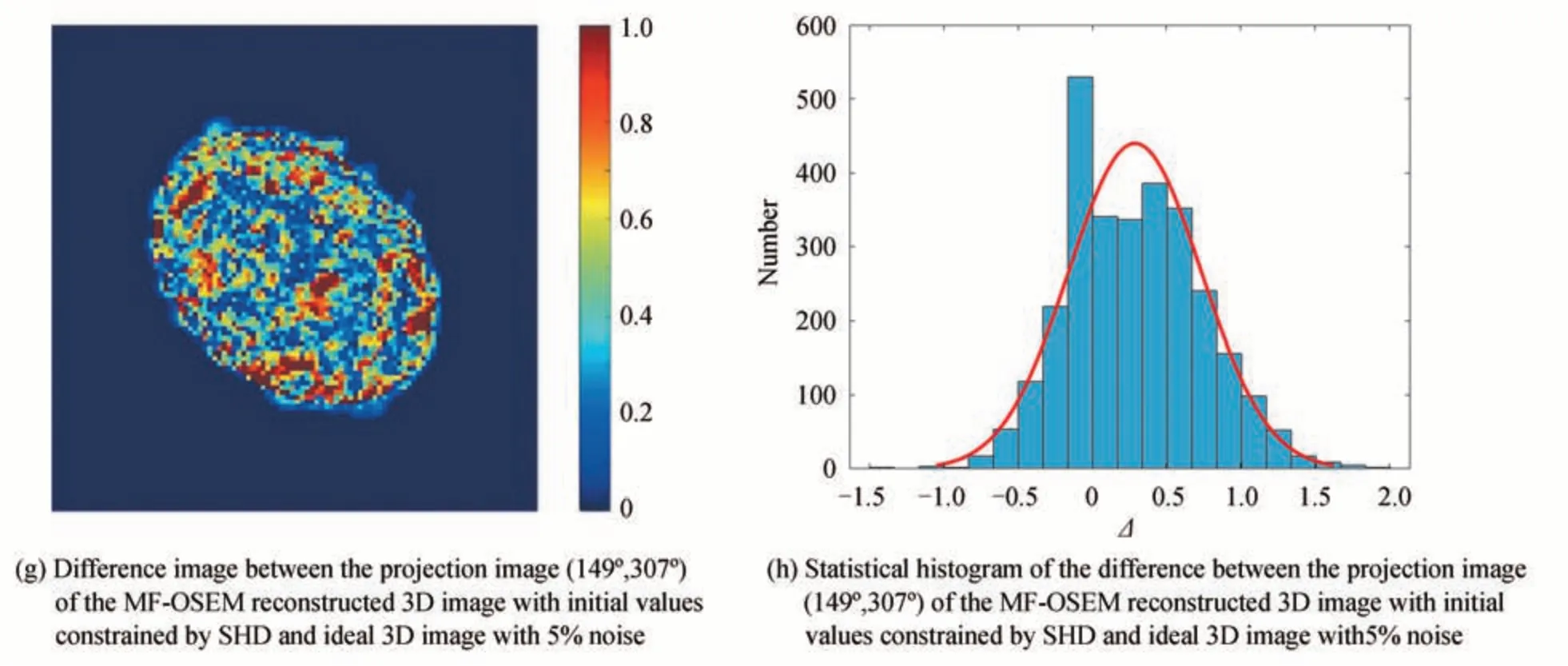
图5 不同噪声水平下球谐函数初值约束的MF-OSEM 算法重建三维图像投影图像与理想投影图像之间的差值及其直方图Fig.5 The difference image and its histogram between the projection image of the MF-OSEM reconstructed 3D image with initial values constrained by SHD and ideal 3D image with different noise

3 重建结果量化比较

在重建图像结果评价中，通常采用一些量化指标进行评价。本文采用峰值信噪比（Peak-Signal to Noise Ratio，PSNR）、均方根误差（Root Mean Squared Error，RMSE）、KL 偏差（Kullback-Leibler divergence）［24］等3 种重建图像质量评价方法对几种图像重建结果进行定量比较。

设理想图像为X，重建图像为Y，P×Q为图像大小，PSNR 定义为

Xmax为图像X的最大值（本文中为1.0）。RMES 定义为

KL 偏差DKL定义为

从式（16）和（17）中可以看出，重建结果评价指标中PSNR 越大，RMSE 越小。KL 偏差越小，表示重建图像与理想图像之间越接近。文中涉及到的几种重建算法量化比较结果如表1所示。

从表1 的结果可以看出，随着噪声水平的提高，所有算法重建结果都会变差，其中OSEM 算法由于在重建过程中没有对噪声进行抑制，其重建结果对噪声最为敏感。球谐函数分解方法虽然依赖于投影角度数量，在本文5 个投影角度情况下，对椭球源依然保持了较好的重建精度。MF-OSEM 算法和基于球谐函数分解的MF-OSEM 算法整体效果较好，采用球谐函数重建结果作为MF-OSEM 的迭代初值可以把EM 类算法的迭代结果限制在初值附近。在本文的量化评价指标下，该方法的重建结果与理想图像之间的差别最小，对噪声适应性也较好。球谐函数分解算法为解析方法，占用计算资源较小，在处理器intel（R）core（TM）i7-4790 CPU@3.6GHz，内存为24GB 的计算资源上完成一次计算的时间约为6 分钟。EM 类迭代算法占用了大部分计算时间，几种EM 类迭代算法所需时间差别不大。本文中EM 算法迭代5 次左右即可收敛，所需时间约为1 455 s（～24 min）。需要说明的是，本文计算的三维结构总像素数为100×100×100，如果要重建更多像素数图像，则需要在较高性能服务器上进行计算以缩短计算时间。

表1 几种三维重建算法效果比较Table 1 The comparison of these three-dimensional image reconstruction algorithms

4 结论

三维图像数据是校验惯性约束聚变靶物理设计的重要结果，极少角度投影三维图像重建存在解空间过大的问题。本文建立了强度空间分布为高斯函数理想椭球源5 个投影角度球谐函数分解、EM 迭代等三维重建算法。球谐函数分解解析重建方法表达能力受投影角度数量的限制，EM 迭代算法只具有局部最优解，基于惯性约束聚变靶为具有一定球对称性的射线源的认识先验，将球谐函数分解解析重建结果作为EM 迭代算法的初始值，从而把EM 迭代算法重建结果约束在球谐函数分解解析结果附近。重建结果及量化评价指标表明，该算法具有良好的效果，对噪声的适应性也较好，可作为类似辐射源极少角度投影三维重建的基准比较算法。下一步，将在实验室构建相应的多光轴成像系统，通过实际实验结果来进一步校验算法的有效性。