投影式幻影成像中局域几何畸变的校正方法研究
杨朝,杨鹏程,张蒙蒙,肖渊,刘晖
(西安工程大学机电工程学院,西安710048)
0 引言
幻影成像也被称为虚拟成像,是将实景造型与幻影相结合,使获得的影像投射在主体模型景观中演示出来[1]。在传统的幻影成像展示平台中,一般在四面锥体顶部放置一块或四块显示屏,屏幕所呈现的是同一个事物在前后左右各个角度的不同的图像,将影像画面投影在四棱锥体表面,在透明四棱锥内部呈现出极具立体感、纵深感的空间三维模型。
由于选用大显示屏将造成系统成本的上升和装置的移动困难,因此选用具有体积小,成像空间不受场地限制,光源装置易于调节,亮度高等优点的投影仪来取代幻影成像平台影像源。但其所带来的问题是投影仪虽然能够在一定程度上实现空间三维模型立体纵深感的表现,但由于投影仪光源处投射出的光束是发散的,且与四面锥体各成像平面并非垂直投影,使其投射至四面锥体上的图像发生几何畸变[2-3]。为保证三维成像的质量及高精度,必须对投影出的图像进行畸变校正处理[4]。
目前针对图像几何畸变的校正方法通常以改进相机标定精度为研究对象,即摄像机标定法[5-6]。2014年GOLJAN M 和FRIDRICH J 提出一种基于摄像机标定的算法,将畸变图像的参数和摄像机参数结合起来,在摄像机标定过程中求解畸变参数[7]。相机标定法虽然其畸变图像校正精度高、可靠性好,但是相机定位标记过程比较复杂,必须利用边缘检测算法确定标定图形边缘,才能确定图形的畸变程度,所以畸变图像校正的精度与相机标定的误差程度紧密相关。
其他比较常见的校正方法,基于线性特征的校正方法[8]、平面仿射投影约束方法[9]、图像插值方法等都是针对图像模板进行研究。AHMED M 和DEVERNAY F 提出了利用直线特征的畸变校正方法,将图中曲线上各点映射到对应的直线上,求解出最优畸变系数[10-11]。需根据畸变图像画面,建立与其相对应的数学模型,然后从畸变图像中提取所需目标的参数,根据数学修正模型,得出畸变校正后的坐标位置,完成畸变图像复原。但该方法应用条件有限,只能适用于小幅度畸变范围情况。
本文在投影式成像系统中通过应用平面透视变换的图像校正算法,将帧缓存中的图片投影到一个新的视平面,根据图像变形前后对应坐标参数关系,用透视误差补偿的方法[12]将坐标变换到其他位置,从而实现畸变图像视觉校正效果。该方法可根据图像不同的畸变情况进行相应有效的校正。
1 幻影成像的光学模型与畸变分析
幻影成像本质是一种光学错觉技术,利用人眼的“视觉欺骗“给人一种立体逼真的感觉。传统的幻影成像光学模型如图1(a),是将同一事物不同角度所成的像分别在四块显示屏中呈现,各角度之间所成的像互不影响且置于四棱锥各表面区域正下方水平放置。显示屏上的光线相互平行且都垂直于平面竖直映射到四棱锥各表面区域对应位置的半透半反膜平面上,使得在四棱锥体各个表面上图像所呈现的位置、大小、角度等参数都一致,所以投影出来的图像较原图像畸变程度较小,在人眼视角的范围内可忽略其影响。

图1 成像光学模型Fig.1 Imaging optical model
本文中投影式光源装置采用投影仪投影,其光学模型如图1(b),是将一张图像完整地投影至四棱锥体上。投影仪成像原理同文献[13]相同,光线以投影仪为光源由中心向外发散,入射至介质与空气的分界面时光线发生折射、反射现象被人眼所接受。与其不同的是本文主要处理因投影仪偏轴角的存在而产生的图像畸变。由光学模型可以看出:投影仪射出的光束并不是从透镜中心位置发射,且每条光束与其竖直线的夹角各不相同,离投影仪越远的光线其竖直夹角就越大,以至于四棱锥体各个表面所成图像均有不同程度的畸变,人眼所观察的投影出来的图像相较于原图像而言产生变形,进而影响到内部三维模型的成像。本文旨在用透视变换算法,以四棱锥体各表面为单元,对各区域不同程度的图像畸变进行相应的校正处理,即对投影式成像局域几何畸变进行校正。
其畸变校正设计要求是:使畸变校正后图像大小与原图像成比例缩放且四棱锥各表面成像的位置相对应,便于在内部空间构成立体模型。为了解决由投影仪投影所带来的畸变影响,如图2所示,几何校正的思路可理解为改变畸变图像中像元点的位置,使其和基准图像对应的像元在同一位置。图像投影至四面锥体的外表面属于可参数化的投影面,按照逆向形变方法,选用透视变换逐点映射的方法进行几何校正,保证图像的精准性。
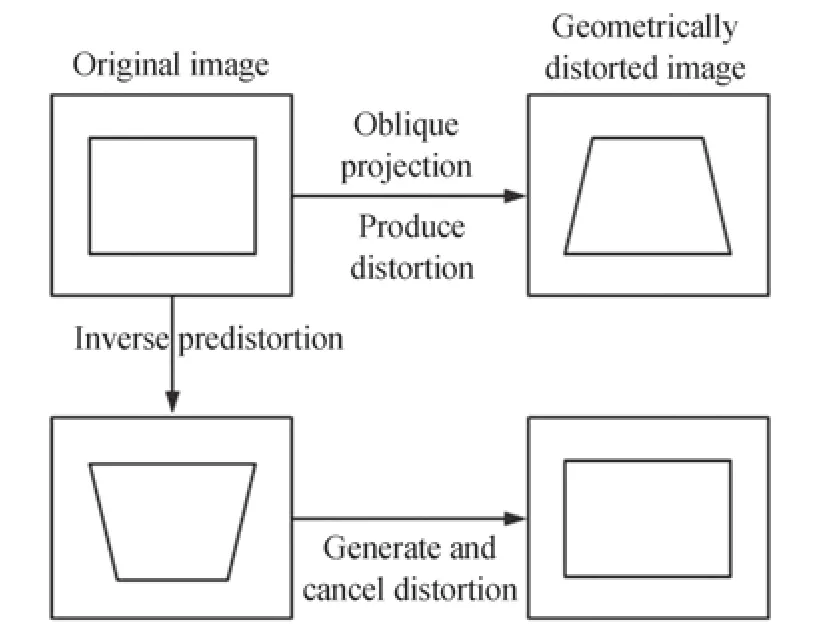
图2 投影畸变校正示意Fig.2 Schematic of projection distortion correction
2 图像畸变校正设计
在校正图像几何畸变的过程中,首先应排除实验仪器带来的误差,其次再对投影所成图像进行校正,畸变校正流程如图3。
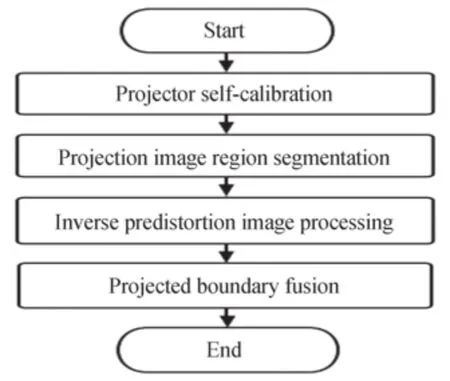
图3 畸变校正流程Fig.3 Distortion correction flow chart
2.1 投影仪投影图像校准
在实验中,每个仪器设备都并非最理想状态,其自身结构、参数对实验都有一定的影响。所以进行畸变校正前,首先应对投影仪自身的参数进行调节,排除投影仪本身所带来的误差,确保投影仪自身对投影图像无影响的前提下,再对投影出来畸变图像进行校正。
首先将投影仪置于四棱锥体顶点正下方,垂直放置于地面以确保投影仪非倾斜放置,进行悬垂校正,如图4所示。在四面锥体顶点位置水平固定光滑且平整的纸板,选择合适的规则图像,调节投影仪参数使之清晰成像。如图4(b),M为四棱锥顶点位置,N为投影图像的中点。理想状态下投影出来的图像中点应与四棱锥顶点位置相重合,为了消除因光束偏轴角所带来的影响,通过直尺等测量工具可测量得到投影仪O点距纸板的垂直距离P,以及四棱锥顶点M距投影图像中心点N的距离Q,则投影光束偏轴角a可表示为

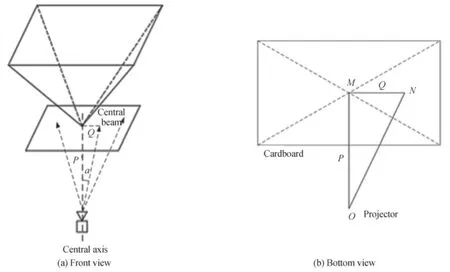
图4 悬垂测试Fig.4 Suspension test
根据式(1)偏轴角a的值,使投影仪在横梁上反向水平移动等距离Q,确保在四面锥体成像介质面上的投影画面中心点与四面锥体锥顶重合。
对投影仪自身参数调整,水平放置投影仪,制作一个15×15 的网格标定板,每个网格为5 mm 的正方形,如图5。取原图像内部一正方形区域,在竖直墙面上投射出清晰、高亮度的图像,使投影像相应的正方形中心点与标定板网格交点重合,通过手动调整投影仪的聚焦环、变焦环、纵横比、自身梯形失真校正、移位等参数,使得各角度保持不变,边长数值精度误差在1~2 mm,令投影出的图像与原图像正方形边长比例一致,通过比例K进行缩放。

图5 投影仪自身校正Fig.5 Projector self-calibration

式中,xi是原图像正方形区域边长,yi是投影图像对应区域边长,且角度相等:β=90°,以便于后续几何畸变的校正工作,K为整数。
2.2 投影图像区域分割
在几何畸变校正时,采用网格图进行校正调整,从图像区域内部选取较小的规则图像为模板,选定特定颜色的正方形模板做特殊标记处理,以防止过于密集的网格造成视觉欺骗,同时更容易把握投影仪缓存图像整体畸变情况,如图6。在编程环境中,将图像中所有像素点看作是二维坐标矩阵形式,通过遍历循环设置图像其开始至结束像素所在的行列数值以及步长,将原图像以对角线分割为均等四份,如图7。

图6 网格图标记Fig.6 Grid marking
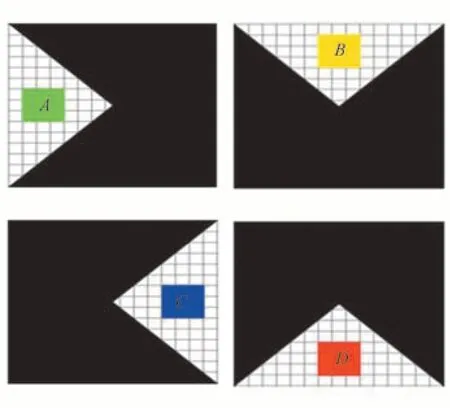
图7 分割图Fig.7 Segmentation image
2.3 逆向预畸变图像处理
2.3.1 畸变图像校正的数学模型
多平面空间三维模型是根据投影图像依据光的反射、折射原理呈现在人们眼中的。动态图像或视频可视为多帧连续图像以时间线有序地叠加放映。因此可以通过对三维模型前后左右的视图逆向预透视畸变,从而达到校正立体三维模型畸变的目的。
由于本文中几何校正是在二维图像与二维图像之间进行校正,其透视变换原理如图8(a),投影矩阵是一个3×3 的矩阵S,选取原图像以及畸变图像内部一一对应的规则形状图像的四个顶点坐标进行变换。
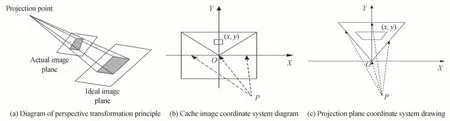
图8 透视及坐标系建模示意图Fig.8 Diagram of perspective and coordinate system modeling
为了确保图像畸变校正设计过程中的精确性,缓存图像和投影图像坐标系的建立采用同一形式,对于缓存图像以分割后的局域图像为单元,如图8(b),以图像中心点即图像对角线分割交点为坐标原点,水平竖直建立坐标系。而对于投影图像则以各四棱锥表面即局域图像为独立单元进行畸变校正处理,图8(c)以四棱锥顶点为坐标原点水平建立x轴,沿投影面过坐标原点垂直于x轴方向建立y轴,然后依次根据各区域缓存图像和投影图像坐标系中对应图像坐标点的关系以同样的方法建立坐标系。通过透视变换公式

2.3.2 图像畸变校正处理
根据透视变换成像原理,对于投影图像各顶点角度和各边长的畸变,主要通过图像各顶点坐标位置的改变进而校正,如图9。
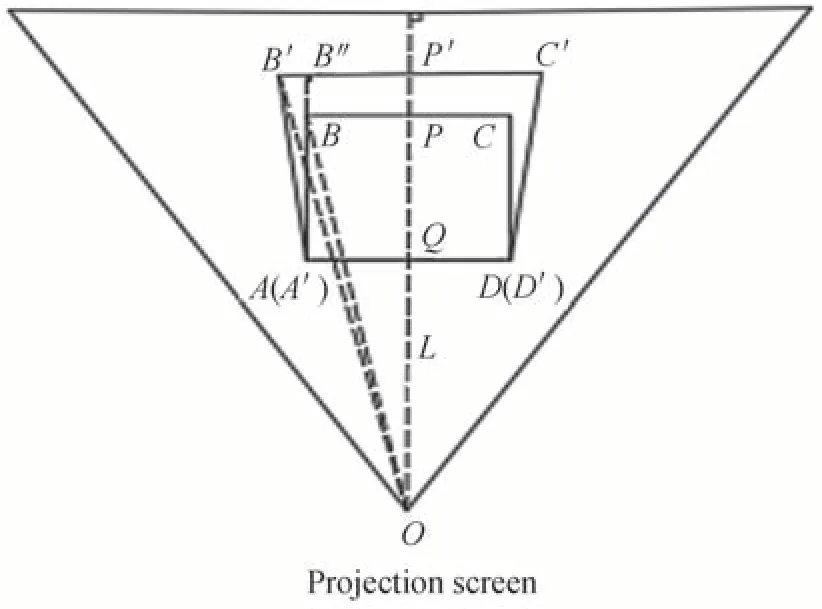
图9 透视成像校正原理Fig.9 Schematic of fluoroscopic imaging correction
图像ABCD是理想的投影图像,而图像A′B′C′D′则为投影畸变产生的图像。以四棱锥顶点O为原点,四棱锥体其中一表面过顶点O所在高线与图像底边距离L为基准,为使各表面图像成像位置相互对应且位于各投影面中心,便于在空间内部形成立体模型。
由于投影图像的基准距离L与原缓存图像对应位置距离成比例关系K,所以理想的投影图像各边长度LAB、LBC、LCD、LDA分别为

式中,lab、lbc、lcd、lda为原缓存图像内特殊正方形各边长值。
根据原图像与畸变图像内部特殊标记的正方形顶点对应坐标的关系,可测量得到畸变图像顶点B′距过原点O所在高线的垂直距离LB′P′。通过与理想图像对应边的差值,可求得畸变图像角点的横、纵偏差值Lx′,Ly′即

再根据实际畸变图像与原图像的比例关系Q,可知在原图像中图像角点的偏差程度Lx,Ly,即

同理,可求出图像其他顶点的畸变程度。令原图像坐标相比于畸变图像逆向变换相等的程度,通过逆向变换矩阵使原图像整体逆向预畸变,进而将原始图像人为地变形为需要的预畸变图像。最终作为投影仪缓存的投影图像,用来抵消因偏轴角a以及光束与投影平面非垂直映射所产生的各区域不同程度的图像畸变问题,达到畸变校正效果。
几何畸变校正完成后,根据两幅图像的权重不同,对图像进行融合,图像融合的计算表达式为

式中,f0(x)、f1(x)表示要融合的目标图像像素值,g(x)则是融合后的新图像像素值。a为图像的权重系数,表示图像融合所参与的光谱信息程度,取值范围在(0~1)之间,当a的值趋近于0 时会使得图像的光谱信息全部丢失,反之会获得图像的全部光谱信息。通过加权求和使得各局部区域图像融合,以保证投影图像整体画面的完整性。
在本文投影式成像系统畸变校正过程中,图像中的网格线对于实验只是一个辅助环境参考标准,便于人们用肉眼去观察图像处理过程中的变化。图像边界融合是否完全的评价主观上依靠人眼来评估融合图像的质量,在不影响投影中心区域物体像的情况下,允许各区域图像边缘少量的重叠。客观上则是根据融合图像本身的统计特征值来衡量,一般用标准差STD 来表示融合图像灰度级分布和对比度,即包含信息的丰富程度,值越大则包含信息越丰富。其计算表达式为
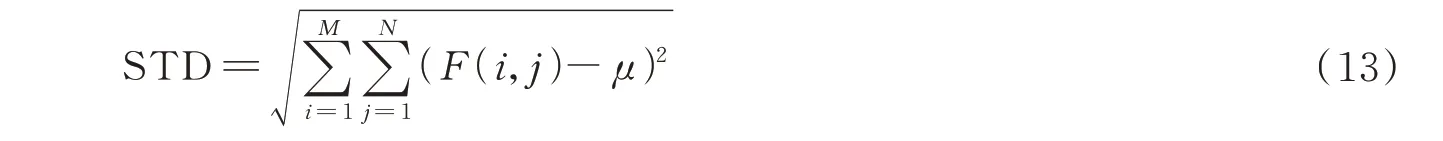
式中,M和N分别代表融合图像的高度和宽度F(i,j)代表融合图像中第i行和第j列像素点的值,μ代表融合图像的均值。畸变图像校正结果如图10(b),为校正后投影仪预畸变缓存图像,相较于图10(a),投影仪缓存图像形状发生了明显的不规则改变,以确保投影出的图像抵消畸变所产生的误差。
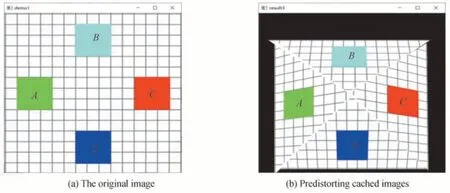
图10 投影仪缓存图像Fig.10 Projector cache image
3 图像几何畸变校正实验及分析
3.1 单平面图像几何畸变校正
本文采用的程序是在python-opencv 环境下调用图形库进行的几何校正设计,具有较高的灵活性以及良好的可移植性。对于单平面投影图像畸变校正,将正方形网格图对角线分割,取其中一个区域投影至四棱锥体表面,如图11(a)所示,投影图像没有完全覆盖在四棱锥体表面上,投影图像的边界未能和其四棱锥体棱边相重合,投影在四棱锥表面的正方形图像明显畸变成长方形,人眼可观察到明显发生畸变。

图11 单平面图像校正Fig.11 Single plane image correction
在python-matplotlib.pyplot 程序中,通过鼠标接触可以获得原图像区域内部特殊标记的正方形顶点坐标,再根据图像畸变程度对正方形小块的对应坐标关系调整,通过透视变换式(3)得到的特殊颜色标记的正方形图案逆向畸变所对应的单应性透视变换矩阵为
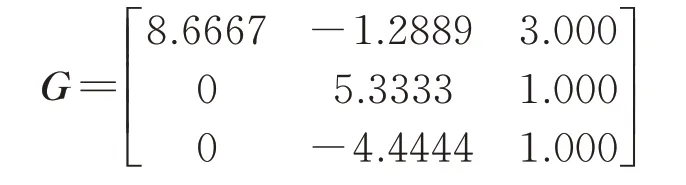
将对应的单应性逆变换矩阵与原图像顶点坐标做矩阵乘积,令原图像整体逆向畸变相等程度抵消投影带来的畸变误差。通过直尺、量角器的测量,特殊颜色标记的正方形其数据如表1~2,绘制成折线图如图12。通过数据可得:畸变图像校正后其边长误差在1~2 mm,角度误差在2°~3°。如图11(b)所示,在人眼视觉观察内,畸变图像有效地得到了校正。

表1 单投影图像投影校正尺寸(mm)Table 1 The projection correction size of single projection image(mm)

表2 单投影图像校正投影内角Table 2 The correction projection angle of single projection image

图12 单投影图像校正数据Fig.12 Correction data of single projection image
3.2 多平面图像几何畸变校正
将投影仪缓存图像投影至四棱锥体表面,得到校正前后图像如图13。图13(a)是投影原图像在四棱锥表面所成的影像,对于一个正方形网格图明显可以看出因偏轴角以及光束与投影平面并非垂直映射,使得四棱锥体各表面投影区域不均匀而产生畸变。图13(b)为源图像逆向畸变后投影所成图像。

图13 多平面图像校正Fig.13 Multiplane image correction
在python-opencv 程序中,根据窗口中图案与四面锥体上投影平面一一对应的顶点坐标,根据原图像与畸变图像对应坐标点之间拉伸、平移、旋转等关系,将畸变图像内部特殊标记正方形根据畸变程度逆向变换用以抵消投影时产生的畸变,通过式(3)得到标注有字样正方形图案逆向畸变所对应的单应性透视变换矩阵G,即
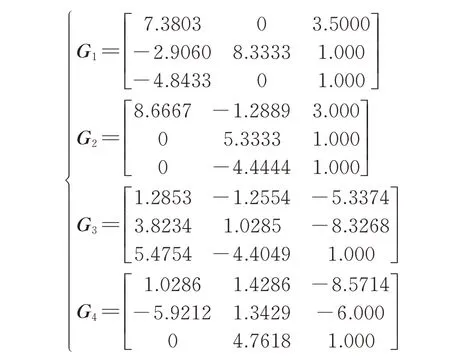
根据四面锥体对应的投影区域,划分出四块纹理区域,之后将正方形图案四个单应性矩阵分别与对应的原图像顶点齐次坐标进行矩阵乘积,从而调整原图像在片段着色器中纹理整体的坐标值。最终实现四面锥体上的投影图像能够组合成空中立体三维模型。
3.3 实验验证分析
选择各表面颜色不同的正方体作为实验测试对象,在四棱锥各表面区域进行畸变校正测试,通过直尺、量角器等测量工具测量投影在四面锥体各表面对应的正方形图像区域校正前与校正后的尺寸及内角,测量值见表3~4,实验测试图如图14。


图14 实验测试图Fig.14 Experimental test chart

表3 校正前图像投影尺寸(mm)Table 3 Image projection size before correction(mm)

表4 校正前图像投影内角Table 4 Image projection angle before correction
在四棱锥各表面正方形区域中,B区域相较于D区域具有更大的长宽比,A区域与C区域长宽比基本相同。表3~4 中数据表明,成像在四棱锥体各个表面的正方形其长度和角度均有一定的畸变,且畸变各不相同。图像边长1、边长3 对应投影仪光轴方向,图像边长2、边长4 对应于水平方向,由于投影仪与四面锥体每个面均有一定的倾斜,导致同一相位投影画面到达四面锥体光程不一致,因此产生畸变。
由于偏轴角的存在,当投影画幕中心点与四面锥体顶点重合时,投影仪与四面锥体顶点不在同一垂直方向上,因此畸变校正前正方形D区域所在四面锥体外表面与投影仪光轴的夹角相较于其他三个外表面更接近垂直。经过透视变换矩阵逆变换,预畸变图像区域在四面锥体上的投影尺寸、内角测量值如表5~6 所示,结合表中正方形尺寸以及内角值,可知基本完成畸变校正。

表5 校正后图像投影尺寸(mm)Table 5 Image projection size after correction(mm)

表6 校正后图像投影内角Table 6 Image projection inner angle after correction
将表3~6 中的数据通过折线图表示出来,且每条线段上的点表示其图像上各边长和角度的值,如图15~16所示。
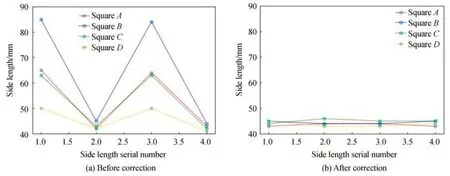
图15 图形边长数据折线图Fig.15 Graph edge length data line chart
投影图像边长以毫米为单位,从图15 中对比每种颜色的正方形折线边长数据,可以明显看出:校正前图像边长总误差范围在7~24 mm,校正后的图像边长误差范围缩小在1~2 mm,校正后图像边长误差从34.4%降低了3.3%,在人眼可忽略的误差范围内有效地降低了图像边长数据的畸变误差。图16 是其图像各顶点角度数据折线图,对比每个正方形各自的角度,校正前图像角度总误差范围在3°~30°内,校正后角度误差缩小在2°~4°范围之内,角度误差从18.3%降低了3.3%,相比校正前图像,畸变图像的角度显著降低。
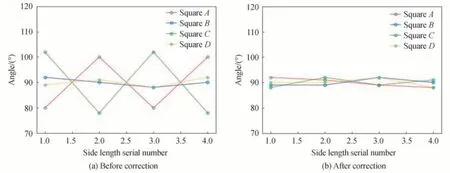
图16 图形角度数据折线图Fig.16 Graph angle data line chart
最终呈现在四面锥体上的正方形区域在尺寸以及内角值上仍有一定的差别,其误差是因为投影仪对图像坐标的重复定位,以及投影仪使用过程中机械内部风扇散热所产生的震动使得投影仪精度及测量坐标值发生轻微变化,但不影响对整个实验结果的分析。实验证明该校正方法实现了对畸变图像的修正,以及各投影面图像相对位置的确定,达到了图像校正设计的要求。
4 结论
本文针对投影式三维展示系统中三维模型的形状失真,提出一种投影图像的局域几何畸变校正方法。首先,将完整图像局域分割,使其投影至四面锥体各表面对应区域。其次,对四个投影平面分别进行透视变换,收集校正前后投影仪投影至四面锥体上图案的长度尺寸以及内角测量数据,分析了相同尺寸的图像畸变不同的原因,实现了对四面锥体各表面以及投影仪位置非正对所引起几何畸变的校正。进一步验证了此方法对局域几何畸变校正的可行性,有效地消除了因投影仪本身光束发散和偏轴角所造成的三维模型图像形状的失真问题,达到了图像校正设计的要求,实现了投影式三维模型的失真校正。