K镜光机结构优化设计与智能误差分配

新其其格，陈忆，季杭馨，王磊，朱永田，张凯，章华涛

（1 中国科学院国家天文台南京天文光学技术研究所，南京210042）

（2 中国科学院天文光学技术重点实验室（南京天文光学技术研究所），南京210042）

（3 中国科学院大学，北京100049）

0 引言

地平式天文望远镜中存在多面反射镜，当望远镜跟踪目标时，望远镜光路中的反射镜间相对转动产生像方视场旋转，同时由于地球自转引起物方视场旋转，因此，在地平式望远镜中独立配置了消旋系统以补偿像旋对成像产生的影响［1］。常见的消旋法有：物理消旋、电子消旋和光学消旋。其中使耐焦后的系统整体旋转的物理消旋方案，由于无法实现在消旋系统后同时加装多个终端仪器，其应用受限；电子消旋则因为需要信号传递，会引起的数据误差和延时性［2］；而光学消旋是在系统光路中添加光学部件，使其与望远镜中的反射镜同步周期性运动来完成消旋，具有“非接触”、“实时”、“全场”等特点，消旋器件可以放置于成像元件前任意位置，安装接口充足的情况下，可在多个光学平台上通用［3］，是目前应用最广泛的消旋方案。

按照使用的光学元件类型，光学消旋可以分为折射式和反射式两种［3］。折射式消旋系统常用的光学棱镜一般为道威棱镜和别汉棱镜，其优点体现在棱镜为整体，各个反射面间的相对位姿可保持不变。随着望远镜口径的增大，棱镜的线性尺寸也不断增加，现有的光学材料已经无法满足需求，同时受光学材料的限制，光线的全波段透射率并不能达到要求，并且存在色散现象，进而导致能量损失。反射式消旋系统则由三块平面反射镜组成，其能量损失小，适用于全波段范围。综上所述，多数地基大口径望远镜均采用反射式光学消旋系统，例如大口径望远镜大型双筒望远镜（Large Binocular Telescope，LBT）、胡克望远镜（Hooker Telescope）、詹姆斯·克拉克·麦克斯韦望远镜（The James Clerk Maxwell Telescope，JCMT）均采用反射式消旋。

国内外对光学消旋的光机设计、误差分析和消旋控制方面已有很多研究。意大利帕多瓦天文台研究人员就LINCNIRVANA 上的两个K 镜的具体情况对消旋系统进行了提高刚性的结构设计并研究了轴承安装对消旋精度的影响［4］；日本研究人员就斯巴鲁望远镜AO188 系统安装的消旋系统的实时和精确跟踪控制方案进行了进一步的研究［5］；土耳其研究人员对DAG（Dogu Anadolu Gozlemevi）放置在Nasmyth 平台的自适应光学仪器的消旋系统进行了加强刚性的设计并分析了其结构变形对仪器性能的影响［6］。国内中科院长春光机所对消旋系统支撑结构的设计和控制系统进行了研究和装调实验［7-11］；国家天文台、云南天文台就消旋机构的理论误差分析和光学系统的设计以及在天文望远镜上的应用进行了研究［12-13］。

在国内外相关研究中都提出了消旋的精确度由K镜光机结构的多个组件（机械旋转不完善，内部对齐不完善，旋转过程中的弯曲）之间的误差耦合决定，在这种情况下，对各组件的误差分配要求严格控制。本文从光机结构设计和光机耦合分析出发，对误差的智能优化分配［14-15］进行了研究，应用蒙特卡洛算法［16-17］结合类粒子群优化算法［18］进行智能优化；就4M 级地平式望远镜上一套K 镜消旋机构进行了优化设计，并对影响消旋机构消旋指向精度的误差源以及工程化过程中的公差分配和零部件选型进行了研究；以K 镜消旋指向精度为前提，进行了装调实验，以验证光机结构设计与误差分配的有效性与准确性。

1 消旋系统理论模型

1.1 反射式消旋系统工作原理

望远镜跟踪过程中，反射式消旋系统作为随动系统始终保持转速为像旋速度的一半，达到其消旋功能。最常用的反射式消旋系统由三块反射镜面呈“K”字型排列组成，分别为KM1，KM2，KM3，其分布方式如图1所示。其中KM1 与KM3 互为120°夹角，同时分别与望远镜主光轴成30°和150°夹角；KM2 工作镜面法线垂直于望远镜主光轴。

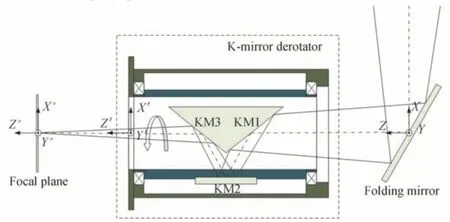
图1 消旋系统（K 镜）光机简图Fig.1 Opto-mechanical schematic diagram of derotator（K-mirror）

1.2 K 镜消旋指向精度数学模型

2 K 镜消旋指向精度智能优化分配

2.1 消旋系统光机结构设计及其误差源分析

基于K 镜消旋系统的工作原理可知，消旋系统由三块反射镜排列成“K”字型。设计的K 镜消旋系统安装于望远镜叉臂上，通光口径为75 mm，其主光轴沿水平方向。在光学元件的选择中，考虑到棱镜消旋系统工作面相对稳定和保持工作面面型的优势，最终选用三棱柱棱镜来保证KM1、KM3 的工作反射面，KM2 选用20 mm 厚的圆形反射镜。为保证光学元件的刚性，并得到优质反射效果，反射镜材料选用微晶玻璃，反射面均镀宽波段高效率的金属介质膜。

消旋机构三维模型如图2所示，在光学元件的支撑结构设计中，KM2 为单独的圆形反射镜，选用背部三点柔性支撑，其中柔性材料选用不锈钢403，以铟钢块为垫块与反射镜背部粘接，柔性支撑连接到KM2 基底结构上，其基底结构进行柔性微调设计，可调节KM2 的位姿。组成KM1、KM3 的棱镜则选用铟钢垫块与基板连接，通过调节铟钢块厚度、斜率来调整其位姿。为达到消旋机构的旋转机能，基板与基底结构均固连到内镜筒上，通过两端角接触球轴承与外筒连接，由电机直驱完成内筒相对外筒的旋转。其中，外筒一端与望远镜叉臂相连，承悬臂状态。

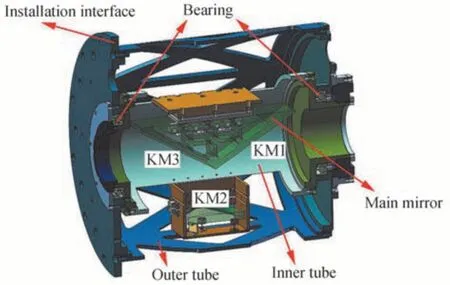
图2 K镜光机结构设计方案Fig.2 Opto-mechanical structure design of K-mirror

根据消旋系统的工作原理与光机结构设计方案，影响K 镜消旋系统指向度的主要因素有KM1、KM2、KM3 的相对位姿和K 镜总装的机械旋转轴与主光轴的偏移与角度。

设计的K 镜消旋机构中不可调节的结构设计误差源如表1所示，其中系统误差随消旋系统的旋转呈现周期性变化，随机误差则在误差范围内随机出现，呈抖动状态。

表1 K 镜消旋机构误差源Table 1 Error sources of K-mirror derotator

2.2 基于类粒子群优化算法进行误差分配

式中，w为权重因子，c1、c2为学习因子，sj为灵敏度因子S=(s1，s2，…，sD)中相对应的元素，dj为每个误差源的公差辨识精度，r1、r2为［0，1］范围内的均匀随机数，在指向精度未达到目标值时pij=pgj=xij。

根据优化路径经过数次迭代，蒙特卡洛算法计算合格率和焦面最大消旋指向精度的迭代优化如图3所示，由图可知在第8 次迭代时收敛。

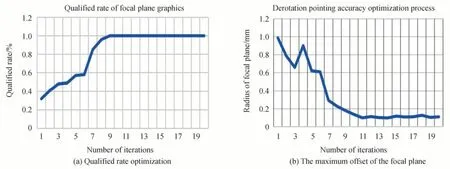
图3 优化迭代收敛图Fig.3 Optimize iterative convergence graph

采用类粒子群优化的结果有多种排列组合方式，考虑满足偏移小、加工成本低、需要调节量少等多因素取值，最终优化结果如表2所示。表2 中的次误差源为主误差源引入的影响指向精度的自由度，其中，Tz、Rx、Ry分别表示因弹性变形导致的KM1、KM2、KM3 沿Z轴的平移和沿X和Y轴的旋转；θ1、θ2、θ3分别为主镜加工中KM1 和KM3 两个表面沿X、Y、Z轴偏转的夹角误差；（X1+X2）/2、（Y1+Y2）/2、（X1-X2）/2、（Y1-Y2）/2 为依据消旋系统左右两个轴承的安装中心位置坐标(X1Y1Z1)与(X2Y2Z2)，计算得到的内镜筒相对外镜筒的安装偏差；IRx、IRy分别为内镜筒中心轴在X和Y轴方向产生的加工角度误差；ORx、ORy分别为外镜筒中心轴在X和Y轴方向产生的加工角度误差。其公差范围相对经验取值法，在结构优化设计与加工精度上可相应放宽数值范围。

表2 关键零部件误差分配优化结果Table 2 Optimization results of key component error distribution

3 优化结果验证

根据表2所示的关键零部件误差分配方案，将表中的次误差源换算到关键零部件尺寸与形位公差上，选择相应的型号及其加工尺寸公差如表3所示。

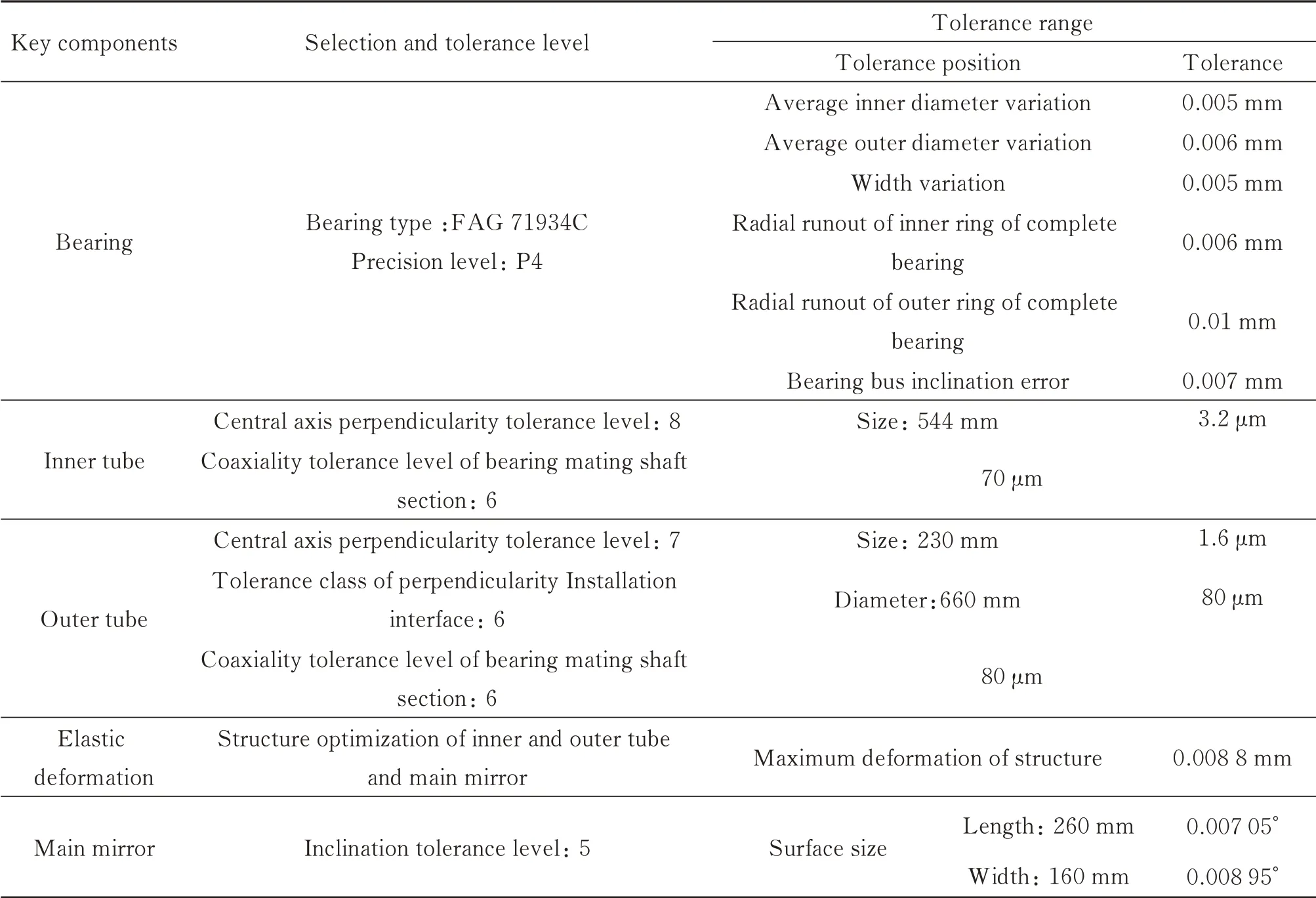
表3 关键零部件公差等级与轴承型号的选择Table 3 Selection of tolerance grades of key components and bearing models

3.1 光机耦合分析验证

对于如K 镜的多个光学元件组成的光机系统，对其进行仿真分析时，应用MATLAB 建立统一的仿真模型，连接光机结构的有限元仿真软件与光线追迹软件进行光机耦合分析。验证结果由光学系统的精度表示。

根据K 镜消旋系统的误差源分析，光机结构在工作过程中的弹性变形会引起反射镜位姿变化，在光机耦合分析中，首先对K 镜进行有限元分析。由于K 镜进行消旋工作时，内镜筒部件相对外镜筒发生旋转，从而光学元件在空间中的位置发生改变，受重力场影响，各反射镜在不同工作位置表现出不同的受力变形状态，因此需要对K 镜处于不同工作位置时的反射镜位姿变化进行均匀采样，提取其位移和旋转变化量。

有限元分析导入模型如图2所示，结构所用材料参数如表4所示，得到结构变形对K 镜反射镜的位姿影响如图4所示，分别为KM1、KM2、KM3 的工作面产生的平移偏差和角度偏差的周期变化的采样拟合。

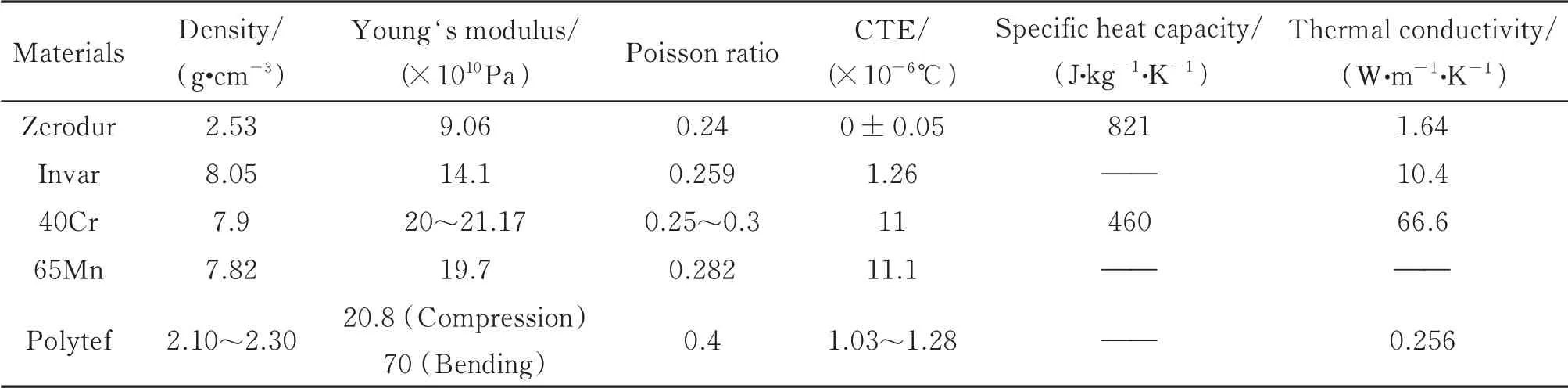
表4 K镜光机结构所用材料参数Table 4 Material parameters of K-mirror

由拟合结果可知，其影响指向性的偏差都随K 镜整体旋转角度呈正弦和余弦的模式，其中AKMi-Tz，AKMi-Rx，AKMi-Ry分别代表K 镜结构在旋转过程中产生的变形引起的KM1、KM2、KM3 在Z方向的平移最大值和沿X、Y轴的旋转最大值，由图4（b）可知，由于KM1 和KM3 为同一块棱镜上的两个反射面，因此KM1-Rx和KM2-Rx的周期变化图形重合。相应的振幅A均小于表3 中的最优结果，分别为AKM1-Tz=0.0069，AKM1-Rx=2.26×10-5，AKM1-Ry=1.62×10-5，AKM2-Tz=0.0106，AKM2-Rx=1.53×10-5，AKM2-Ry=2.33×10-6，AKM3-Tz=0.0054，AKM3-Rx=2.26×10-5，AKM3-Ry=1.96×10-6。

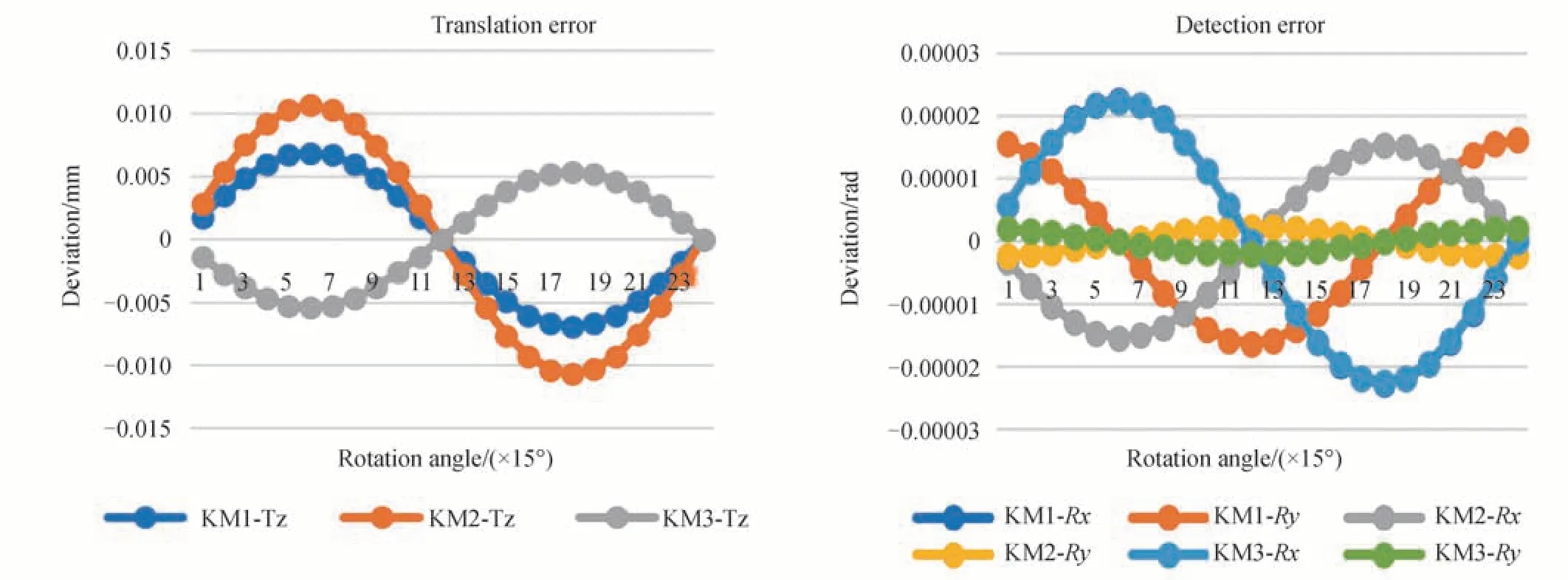
图4 有限元分析得到的KM1、KM2、KM3 的位姿周期变化拟合Fig.4 Fitting graphs of KM1，KM2，and KM3 pose cycle changes obtained by finite element analysis

根据式（6）和（7），应用仿真软件建立消旋系统仿真模型，模拟模型焦面位置为从望远镜中转镜开始的距离1.94 m，图4所示的误差对应式（6）中的MF-Ki(θ)，TF-Ki(θ)。将主镜加工产品实际三坐标测量结果和轴承供应商提供的轴承误差带入仿真模型中，轴承选型和内外镜筒加工引入的误差在公差范围内，以100 个满足条件的随机误差求得在仿真模型焦面上形成的图形，其中半径最大的图形如图5所示。根据式（20）求得最大指向性偏差角度。

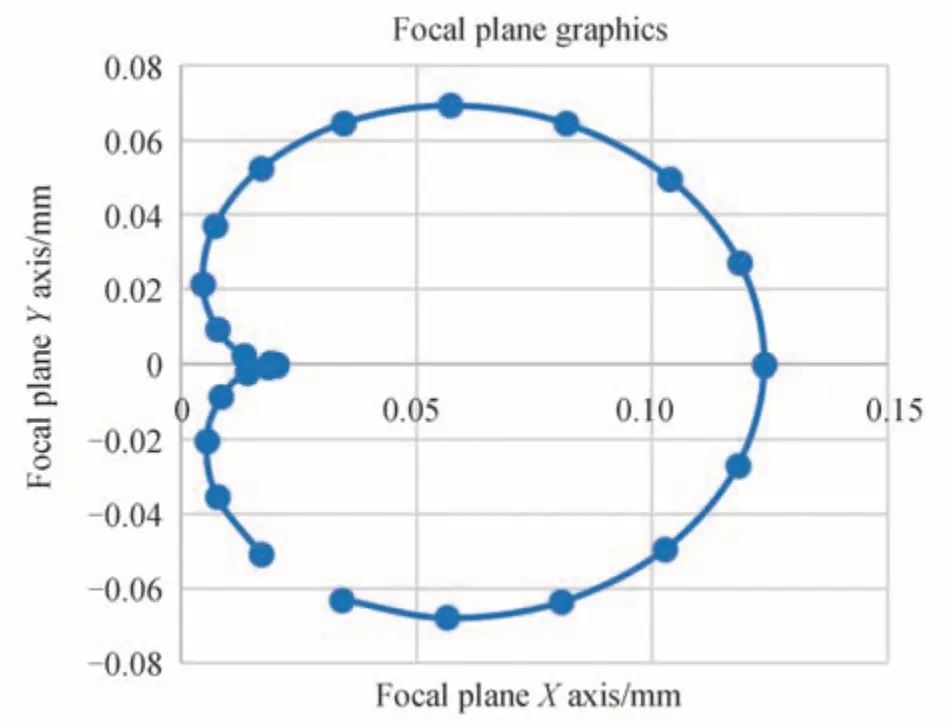
图5 误差仿真分析焦面图形Fig.5 Focal plane graphics from error simulation analysis

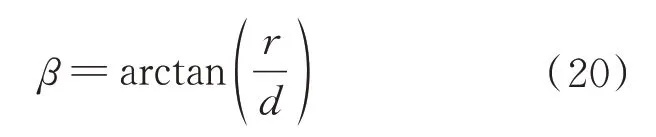
式中，r为在焦面上图形的最大直径，d为焦面距离KM3 中心的直线距离，β为消旋指向精度值。在模拟仿真中r=0.079 208 mm，d=2 350 mm，代入式（20）得到指向偏差β=6.95′′。

3.2 实验验证

消旋机构实际装调实验平台如图6所示，在进行装调中，为保证消旋系统的出射光源在探测器内形成的偏移误差来源于消旋机构本身，对入射光源进行光路修正，保证入射光源的指向稳定性。

图6 K 镜装调实验平台Fig.6 Experimental bench of K-mirror

在基础装配后，对K 镜主镜和KM2 子镜进行位姿调整，主要通过改变垫片的尺寸对主镜的倾斜和Y向平移进行调节，对KM2 子镜进行Y向调节和倾斜调节，在调解过程中可进行相互补偿。其中，Z向具有安装基准面无需调节。实验室调节状态下得到最优调节结果。调节最优情况下，截取探测器上显示的图形，寻找图形的最小外接圆，得到的探测器图形如图7所示，其最小外接圆半径占像面45个像元（像元大小：5.2 μm），将探测器图形所测得到的图像半径带入式（20）中，得到光经过K 镜后产生的消旋指向精度为β=14.24′。

仿真验证时，其有限元分析结果小于表2所示的误差分配结果，因此仿真结果小于数值优化得到的指向精度。并且仿真时，假设轴承、内镜筒、外镜筒等关键零部件的安装误差处于理想状态下，因此其仿真误差小于实际装调误差。

4 结论

本文针对地平式天文光谱仪的消旋需求，对一套悬臂式K 镜消旋系统进行了优化设计。对光机系统的多误差源影响指向性问题，根据消旋系统工作原理和光机结构设计方案找到不可调节误差源，并提出了类粒子群优化方法，利用该优化方法对其误差源进行智能优化，得到了可收敛的误差优化分配结果。对最终设计方案和公差分配方案进行了光机耦合误差分析和实验验证，仿真分析结果表明最大消旋指向精度为6.95′′，实验调节中探测器显示图形占像面45 个像元，即K 镜的消旋指向精度为14.24′。提出的基于类粒子群算法结合蒙特卡洛算法的智能优化方法对各误差源进行了合理的公差分配，可为以后智能误差分配高精度光机仪器的误差源、指导工程化的加工公差分配和结构优化极限提供参考。