大气湍流环境下光斑中心定位算法研究

吴鹏飞，王辉亮，雷思琛，党帅

（1 西安理工大学自动化与信息工程学院，西安710048）

（2 西安理工大学国际工学院，西安710054）

0 引言

光斑中心定位是一种激光光斑能量中心位置的精确定位技术，是光学测量中常用的关键技术，在激光通信、目标跟踪、武器系统、激光雷达、激光测距领域有着广泛的应用。在大气激光通信中，激光经过湍流扰动的大气后会出现光束漂移、扩展和光强起伏等现象，导致接收天线探测到不同程度的畸变光斑［1］，而快速、精确定位出成像光斑的中心，是实现激光通信的关键技术之一。高准确性、高精度的光斑定位算法可在保证通信链路稳定建立的前提（接收孔径的光功率稳定维持在探测阈值之上）下，有效地减少伺服机构的促动位移、促动频率，提高系统的工作效率。因此研究湍流环境中的高效光斑定位算法，对无线激光通信具有重要意义。

目前在系统中使用的光斑定位方法有质心法、形心法、Hough 变换法［2］、椭圆拟合法［3］、高斯拟合法［4］等。质心法、形心法对均匀光斑能够精确定位，计算速度快，对于对称性良好、分布均匀的光斑具有较高的定位精度，当光斑畸变程度变大，精度也会有一定程度的降低［5］。周红锋等［5］采用迭代阈值法进行粗定位，然后进行插值处理，实现CCD 光斑中心的亚像素定位，定位精度和稳定性有一定程度提升；张飞舟等［6］对碎斑特征进行了统计分析，随着湍流强度的增加和光束质量变差，总光斑扩大，碎斑数目增多，而碎斑半径变化不大；沈宝良等［7］通过仿真，对湍流强度对光斑质心定位精度的影响给出了统计偏差曲线，结果表明，提高CCD 相机中心部分像素可信度，可以提升整体定位精度。刘云清、姜会林等［8］结合大气湍流和探测器，针对质心算法和形心跟踪法，进行深入分析，得到并实验验证了在大气条件下形心算法的跟踪误差小于质心误差的结论，但湍流情况下形心法的稳定性以及精度，还可以被继续提升。吴泽楷等［9］在圆拟合基础上改进了算法，加入了采集处理，去噪滤波，以及多次迭代等预处理方法，提高了检测光斑中心位置的精确度，增强了抗干扰能力。2019年WANG X 等提出了一种基于功率加权的亚像素定位算法［10］，将其应用于摆倾仪CCD测量系统并进行实验验证，实验表明，该算法在室内无湍流环境下对规则光斑的定位精度较高。在湍流环境下定位稳定性有待进一步提升。而目前的自适应光学技术可以实时探测并校正由大气湍流引起的光束波前相位畸变，但仍然限于计算处理能力、计算速度和测量误差等因素。

本文在深入分析传统形心法（Centroid Algorithm，CA）、质心法（Barycenter Algorithm，BA）、非线性权重质心定位算法（Nonlinear Weighted Barycenter Algorithm，NWB）以及受湍流影响的畸变光斑的基础上，对比分析了不同算法的定位精度及稳定性，通过改进传统光斑定位算法，提出了滑动加权质心定位算法（Sliding Weighted Barycenter Algorithm，SWB），为ATP（Acquisition，Pointing and Tacking）系统下光斑中心的精确定位提供了理论及实验依据。

1 改进算法的分析

1.1 算法概述

首先改进阈值分割方法，提高光斑定位的精度，并利用短时间内的叠加图像作为参考图像，去除光斑噪声背景并实现中心噪声补偿，最大程度保留光斑有效灰度范围；接着通过中值滤波和闭运算进行进一步处理，在此基础上，提出滑动加权质心定位算法，先由非线性权重质心定位算法作为粗定位，利用短时间内的光斑图像的整体偏移向量，反向滑动补偿到粗定位中心，实现对光斑中心的精确定位。粗定位点可以反映当前图像的光斑中心的光强最大点，但是定位瞬时偏移步长过大会导致连续定位稳定性差，因此将短时间内的光斑图像的整体偏移向量反向滑动补偿到粗定位中心，既能保证光斑中心的光强保持在尽可能大的范围，同时也一定程度减小了连续定位的瞬时偏移步长，提高了连续定位稳定性。

1.2 众数自适应阈值分割方法

在光斑图像定位中，合理的阈值选取方法，可以有效地滤除背景噪声干扰，在提高定位精度的同时减少运算量，最大程度保留光斑的有效灰度值。自适应阈值法（Adaptive Threshold Method，ATM）［11］计算简单，有良好的阈值分割效果，不同情况的方差乘以系数K（一般取5～15），K值改变会使光斑有效分割区域发生变化，影响定位精度，因此对该方法作了改进，提出一种众数自适应阈值方法（Mode Adaptive Threshold Method）。改进后方法见式（1）。

式中，H为原始图像，V为众数自适应阈值的计算结果，Ravg为图像灰度平均值，M0为图像灰度的众数。该方法用灰度图像众数值替代了原始的加权方差，在实际的灰度光斑图像中，背景相对于目标占比较大，而众数不仅可以有体现背景中噪声的大小，同时也最大程度保留了光斑图像灰度信息，为下一步光斑图像处理定位提供了一个更加精准有效的范围。

模拟了标准高斯光斑图像，除了以上两种阈值分割方法，还使用了最大类间方差法［12］（Maximization of interclass variance method）和迭代法［5］（Iterative method），并结合两种不同定位算法，求得定位点离标准中心定位偏差大小，见表1。

由表1 可知，众数自适应阈值分割方法相较于传统自适应阈值法，能够提高规则光斑在非线性权重质心定位算法以及质心法下的中心定位精度。在非线性权重质心定位算法下，定位精度最大可以提高5 倍以上。

表1 不同算法下定位点离标准中心偏移量/像素Table 1 Offsets of registration point from standard center under different algorithms/pixel

1.3 滑动加权质心定位算法

质心法的抗噪声性能差，精度有限，非线性权重质心法的抗噪能力有所改善，对规则光斑定位精度较高，但在对畸变光斑的定位上稳定性不足。因此提出滑动加权质心定位算法（Sliding Weighted Barycenter algorithm）。光斑图像定位算法流程图如图1所示。

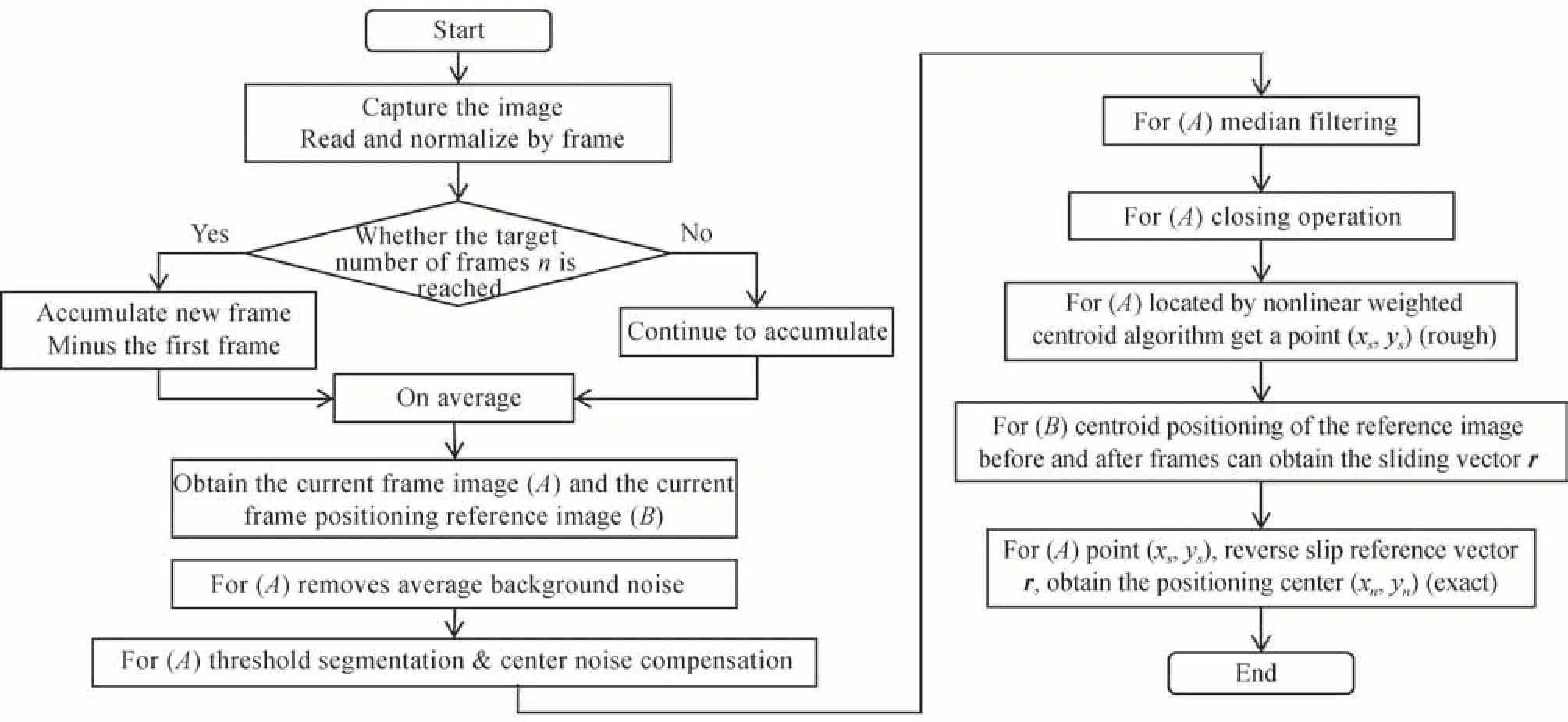
图1 光斑图像定位算法流程图Fig.1 Principles of image detection algorithm flow chart

首先对图像进行归一化处理并读入图像，对CCD 相机捕获的图像进行处理，需要先将真彩色图像RGB转换为灰度强度图像。把RGB 的3 个通道的分量按照一定的比例计算到灰度图像中，如式（2）所示。

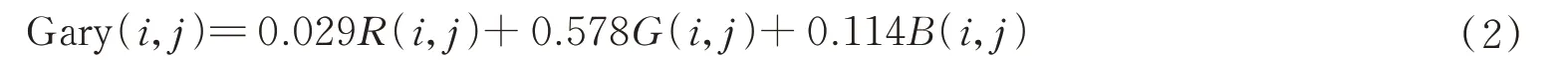
式中，Gray（i，j）表示原图像的灰度值

对图像读入进行灰度归一化处理：采集到的CCD 光斑为8 位的灰度图像，256 个灰度级，但由于采集时曝光程度等因素的影响，图像的灰度级集中在一个或者几个灰度级区段，这时可以采用灰度拉伸的方法将图像扩展到256 个灰度级。灰度变换归一化见式（3）。

式中，I（i，j）表示变换后图像的灰度值，min=0 和max=255 分别表示原图像的最小灰度值、最大灰度值。

开始叠加图像，设置叠加图像的帧数上限值为n（此处令n取10）；生成每一张当前帧图像A的当前帧参考图像B，具体处理流程见图1。由参考图像B阈值VB可得到（VB对应的灰度值大小k），作为平均背景噪声灰度值大小，由式（4）可得到去背景处理后图像。

中心补偿作用：光斑本身已经处于失真状态，可以通过滤波处理阈值范围以内的噪声，而在去背景操作中，会丢失图像中心像素的有效信息，因此需要把中心处去掉的背景噪声补偿回来，再通过滤波进行滤除。VA为当前帧图像A去背景后图像的阈值，具体操作见式（5）。

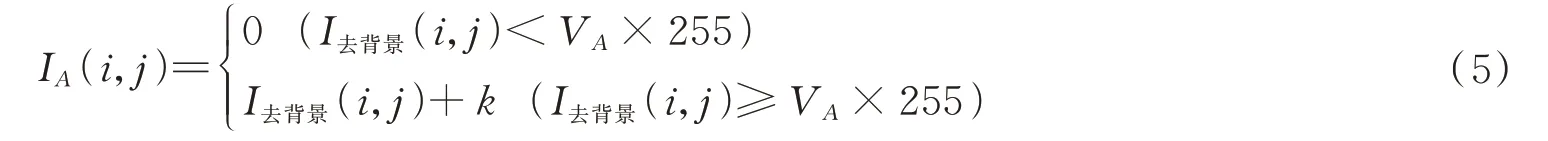
然后再进行中值滤波，中值滤波是把数字图像中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点。W为二维模板，此处选取为9×9 区域二维滑动模板。将板内像素按照像素值的大小进行排序，生成二维数据序列。其中，IA（x，y）、J（x，y）分别为原始图像和处理后图像。二维中值滤波输出过程见式（6）。

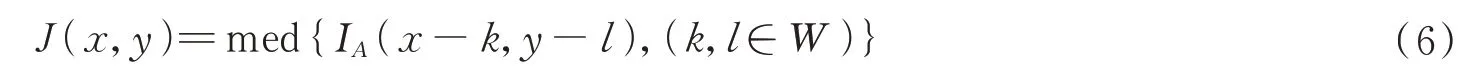
最后进行闭运算处理，闭运算通常用来填充目标内细小孔洞，连接断开的邻接目标，平滑其边缘的同时并不明显改变其面积。闭运算先膨胀再腐蚀。对于一个给定的目标图像J，创建一个菱形的结构元素S，其参数15 是从结构化元素原点到其点的距离。膨胀运算子可以描述为：将J中的每一个点x扩大为S［x］，其集合形式定义为式（7），腐蚀是形态学的基本算子之一，图像腐蚀可以描述见式（8）。

闭运算处理过程见式（9）。

经过中值滤波，闭运算处理，得到预处理后的当前帧图像A。图像闭运算，有助于关闭目标光斑由于外界干扰产生的空隙，同时增强图像定位算法的稳定性以及定位精度。为了展示预处理的效果，对实验条件下得到的2.4 km 和10.2 km 距离激光实验捕获的光斑分别进行操作。操作1：原图→阈值分割→滤波，操作2：原图→去背景→阈值分割&噪声补偿→滤波。

一般来说，峰值信噪比（Peak Signal-To-Noise Ratio，PSNR）表示一个信号最大可能功率和影响它表示精度的噪声功率的比值，而均方误差（Mean Square Error，MSE）代表原始信号和处理后信号之间的均方误差。由表2 可以看出，操作2 处理的图像得到的MSE 小于操作1，以及PSNR 大于操作1，说明操作2 对噪声的处理效果更好。

表2 光斑处理过程效果分析Table 2 Effect analysis of spot processing

定位部分：对当前帧图像A进行粗定位，使用非线性权重质心法，由式（10）得到当前帧图像A的粗定位点（xs，ys），式中g（x，y）为像素位置（i，j）的灰度值；此处p是权重，定义p=2［10］，得到当前帧图像A的粗定位点（xs，ys）。每个当前帧图像A对应一个当前帧参考图像B，将上一帧图像的当前帧参考图像B上一帧以及当前帧图像的当前帧参考图像B当前帧分别进行质心定位，得到光斑整体移动向量r；滑动示意图见图2所示。

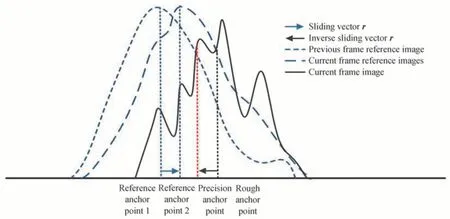
图2 光斑定位滑动补偿示意图Fig.2 Diagram of spot sliding compensation positioning

由向量r对粗定位点（xs，ys）进行反向补偿，由式（11）得到精定位点坐标（xn，yn）。

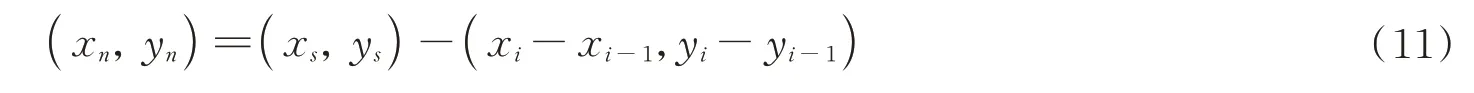
滑动加权质心定位算法本质上是在非线性权重质心定位算法对于规则光斑定位精度高的优点上，通过滑动补偿机制，尽可能减小在通信中由于光斑闪烁漂移带来的定位误差，弥补它对畸变光斑定位稳定性差的问题。滑动向量可以反映出短时间内光斑整体的移动范围，由向量反向滑动可以补偿非线性权重质心定位算法定位偏差，从而提高定位的稳定性。定位参考图像有两个作用：一是定位参考图像可以直接求阈值，快速得到平均背景噪声大小，帮助当前帧图像进行去背景操作，精准去除背景噪声。二是在当前帧图像在粗定位以后，参考帧图像得到的向量可以反向滑动补偿粗定位结果，使得定位效果更好，更稳定。

2 理论仿真分析

2.1 不同湍流强度下的光斑仿真

使用功率谱反演法仿真大气湍流相位屏，模拟不同强度下的湍流大气，为了更接近理论值，对相位屏进行了次谐波补偿［13］，为了评估生成相位屏的准确性，将模拟相位屏的相位结构函数与理论值进行比较。p为谐波次数，r0为大气相干直径，也称为Fried 参数，描述了接收通过大气湍流传播能量的单孔有效直径，用来表征大气湍流强度，对于可见波长和垂直视野，r0的值通常为0.05～0.1 m，此处，将r0取为0.1 m，该物理量近似代表了在不同气象条件下相干直径为0.1 m 的大气湍流强度。图3 为不同谐波次数下的相位结构函数与理论值之间的比较。使用p=25 时的谐波次数进行相位屏的模拟生成。

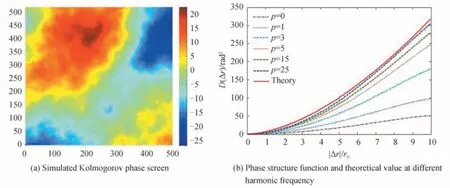
图3 大气湍流相位屏仿真Fig.3 Phase screen simulation of atmospheric turbulence

图4 仿真高斯光束经过不同强度湍流相位屏的光斑Fig.4 Simulate the spot of Gaussian beam passing through the turbulent phase screen of different intensities

2.2 理论定位结果

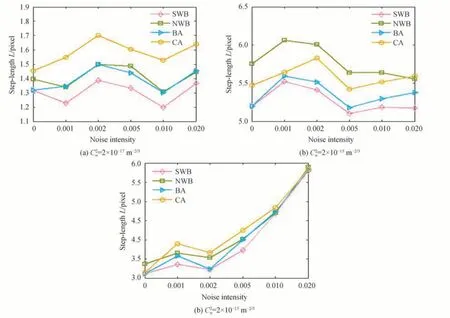
图5 不同强度高斯噪声下四种算法的光斑图像距离中心定位间距Fig.5 Positioning spacing between four algorithms in different intensity Gaussian noise

以定位点为中心，依据光斑图像大小以及光斑的尺寸，此处取半径R=30 pixel 圆形掩膜，得到掩膜内的像素强度求平均。结果分别如图6（a）～（c）所示。可以看出，在弱、中湍流环境下，噪声的改变对光斑中心偏移的影响不大，当湍流强度到达强湍流时，光斑中心的偏移随着噪声的变大而变大。而掩膜面积内像素强度可以反映出当前定位点周围的光功率大小。光功率越大，定位效果越好。

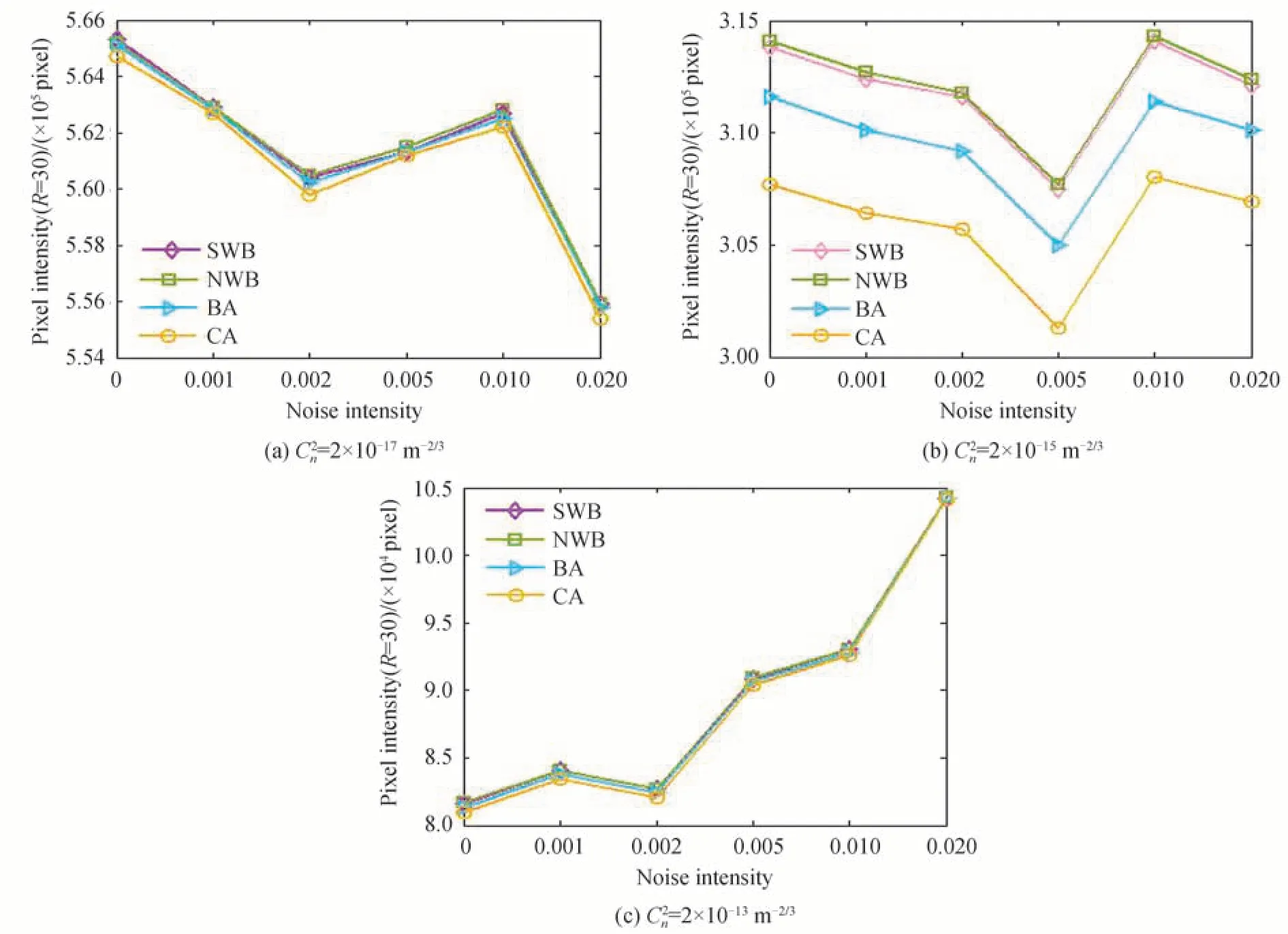
图6 不同强度高斯噪声下四种算法的光斑图像掩膜内像素强度Fig.6 Pixel intensity of spot image mask based on four positioning algorithms under different intensity gaussian noise

可以看出，提出的SWB 定位算法在不同湍流下连续光斑定位中心点的偏移步长最小，相比NWB 定位算法，连续光斑定位中心点的偏移步长最大可以减小10%，相比BA 定位算法，连续光斑定位中心点的偏移步长最大可以减小8.9%，相比CA 定位算法，连续光斑定位中心点的偏移步长最大可以减小21.5%，在掩膜内像素强度方面，SWB 定位算法的像素强度不及NWB 定位算法，但仍优于传统的BA 法和CA 法。同时结合定位点的偏移稳定性，综合而言，SWB 定位算法的定位精度和稳定性最好。

3 实验验证分析

西安理工大学实验团队分别在10.2 km、2.4 km 距离下搭建了激光通信链路，本部分激光通信链路的光路图如图7所示，并对情况作简单介绍。

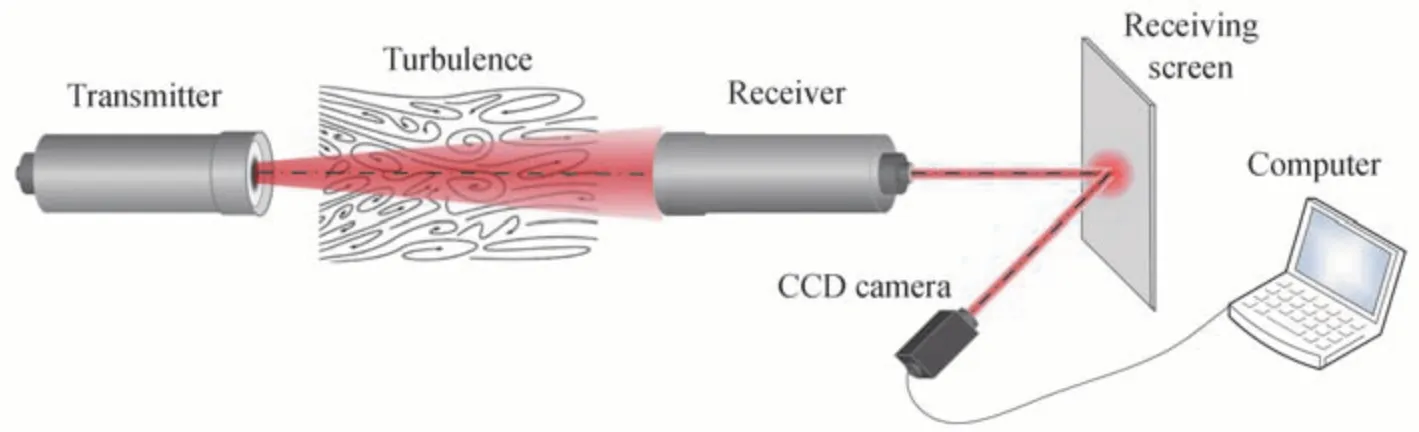
图7 激光通信链路图Fig.7 Laser communication link

图8 为10.2 km 初始指向通信实验［16］，实验发射端位于西安理工大学金花校区教学六号楼8 楼东侧，收端位于西安市肖家寨351 乡道附近。10.2 km 初始指向通信实验使用NKT Potonics 生产的1 550 nm 光纤激光器作为信号光源，经过光纤放大器后通过开普勒透射式天线（孔径D=94 mm）发出，输出功率在200 mW范围内可调节，经过光纤放大器后的发射光功率为600 mW。接收天线采用马卡斯托折返式望远镜结构，口径为300 mm。由于光束到达漫反射屏的尺寸较大，且图像中有块黑色正方形（接收天线在屏幕上的投影），因此数据采用了摄影机记录的视频中截取的光斑。在初始指向通信实验中，采用摄像机正对光束发射方向记录连续光斑视频，从视频中按帧截取光斑图像数据。

图8 10.2 km 通信链路Fig.8 10.2 km communication link

图9 为2.4 km 通信链路［17］，2.4 km 为实验中的激光通信链路的直线距离，其中发端位于西安市新东尚小区某建筑物内，收端位于西安理工大学学科2 号楼8 楼最东侧，实验中使用西安华科光电有限公司生产的DH650-100-5 型650 nm 的半导体激光器进行激光的发射，输出功率为100 mW。收端采用西光SICONG 牌3309-02 型马卡天文望远镜进行接收。使用维视公司生产的MV-E 千兆网工业相机进行光斑图像的拍摄。

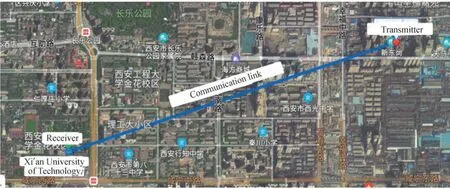
图9 2.4 km 通信链路Fig.9 2.4 km communication link

分别得到连续的若干组10.2 km 光斑图像，如图10所示（在参考文献［16］实验条件下，实验时间9月30日，09：00-12：00 时，采用摄像机，正对光束发射方向记录的连续光斑视频，从视频中按帧截取的图像。由于光束到达漫反射屏的尺寸较大，且图像中有块黑色正方形（接收天线在屏幕上的投影），因此采用摄影机记录的视频中截取的光斑）和2.4 km 光斑图像如图13所示（在参考文献［17］实验条件下，实验时间8月15日，19：00-21：00 时，在固定位置，CCD 相机正对接收的光斑图像）。

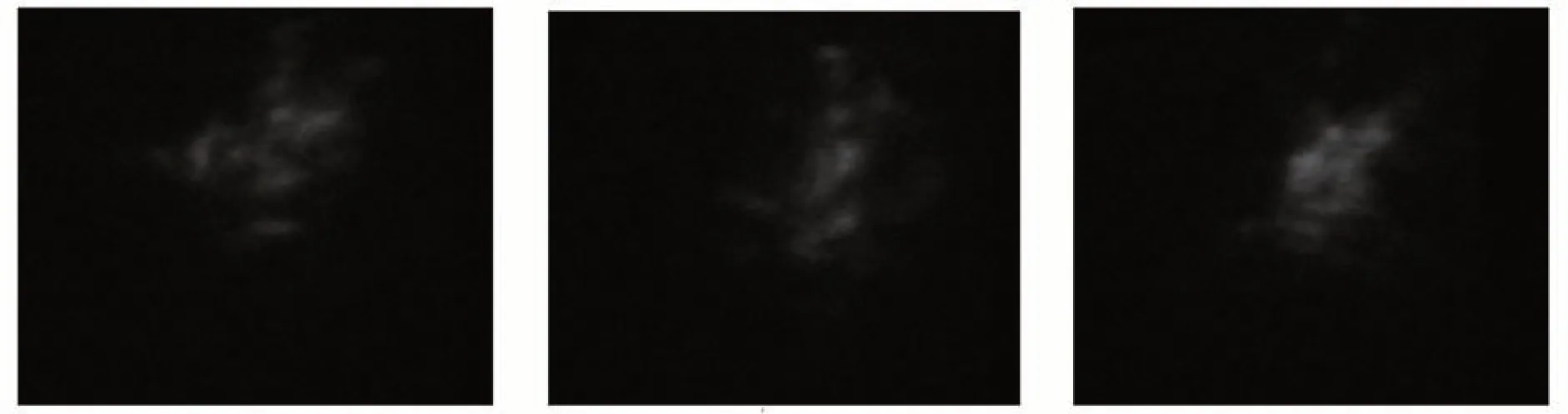
图10 10.2 km 实验捕获的实际光斑图像Fig.10 Actual spot image captured in 10.2 km experiment

用SWB 算法、NWB 算法、BA 法、CA 法对光斑图像进行定位，得到若干定位点，以定位点为圆心，取不同半径掩膜，可求得每个定位点对应的掩膜面积内像素强度，掩膜面积内像素强度越高，说明捕捉到的光斑强度越高，定位效果越好，连续定位点间间距越小，说明定位算法稳定性越好。

取得10.2 km 光斑图像，此处单个图像大小均为600 像素×500 像素，由于接收端的光斑图像大小以及光斑大小占图像比例，此处设定掩膜半径为30、60 像素，随机取得其中一组数据，图11 为四种算法下10.2 km 100张连续光斑图像取不同半径掩膜内像素强度，图12 为不同算法下10.2 km 100 张光斑图像间定位间距。且由于实验条件下远距离激光传输，存在较强光斑闪烁漂移，连续定位中心偏移将会远大于模拟环境下的值，但仍然保持在对应图像最小掩膜范围的中心区域。

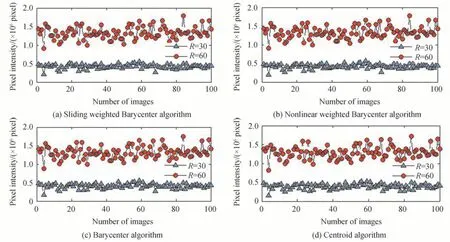
图11 不同算法下10.2 km 100 张光斑图像取不同半径掩膜内像素强度Fig.11 Intensity of the pixels in mask from 10.2 km spot image under different algorithms

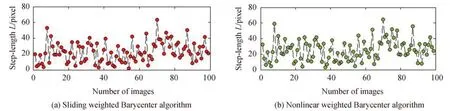
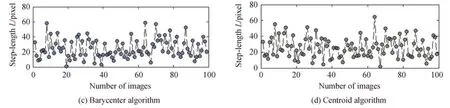
图12 不同算法下10.2 km100 张光斑图像间定位间距Fig.12 Location distance between 10.2 km spot images based on different algorithms

表3 为10.2 km 光斑数据处理结果。

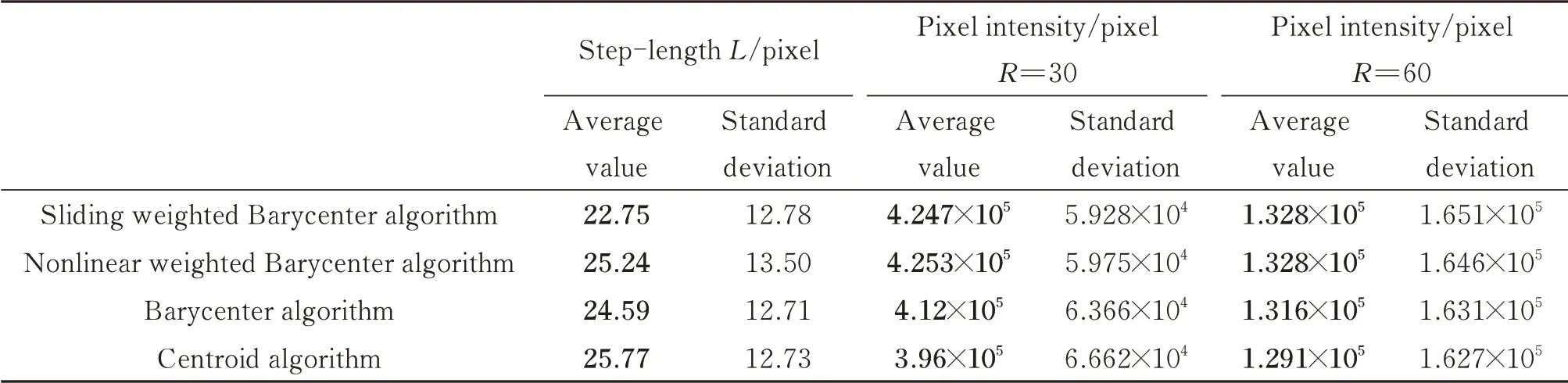
表3 10.2 km 光斑处理过程效果分析Table 3 Effect analysis of 10.2 km spot processing

取得若干组2.4 km 光斑图像如图13所示，此处单个图像大小均为1 600 像素×1 200 像素大小，由于接收端的光斑图像大小以及光斑大小占图像比例，此处设定掩膜半径为80、110 像素，随机取得其中一组数据，图14 为四种算法下2.4 km 100 张光斑图像取不同半径掩膜内像素强度，图15 为不同算法下2.4 km 100 张光斑图像间定位间距。

图13 2.4 km 实验捕获的实际光斑图像Fig.13 Actual spot image captured in 2.4 km experiment

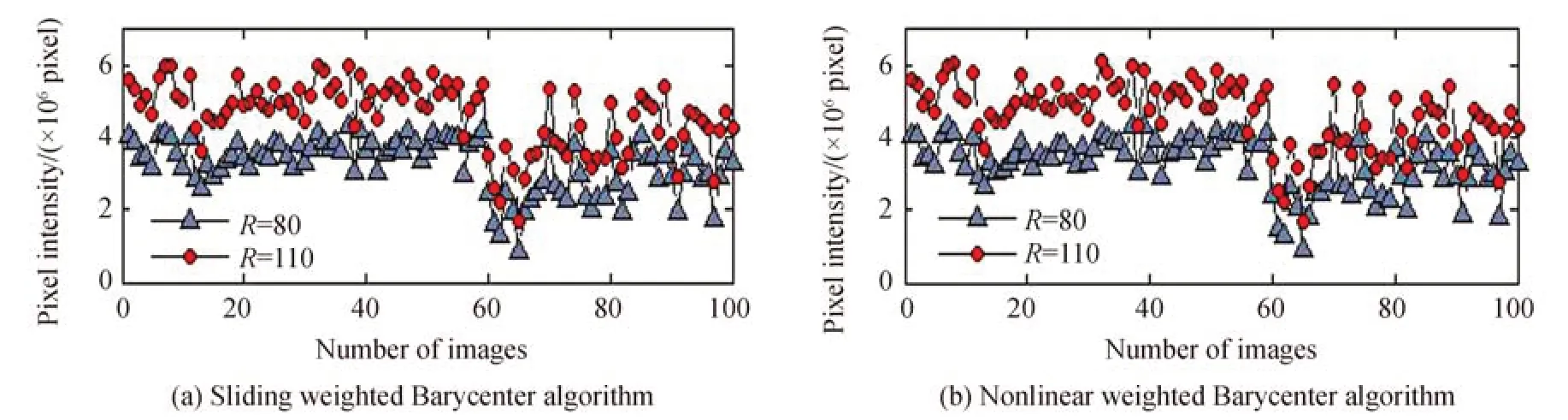
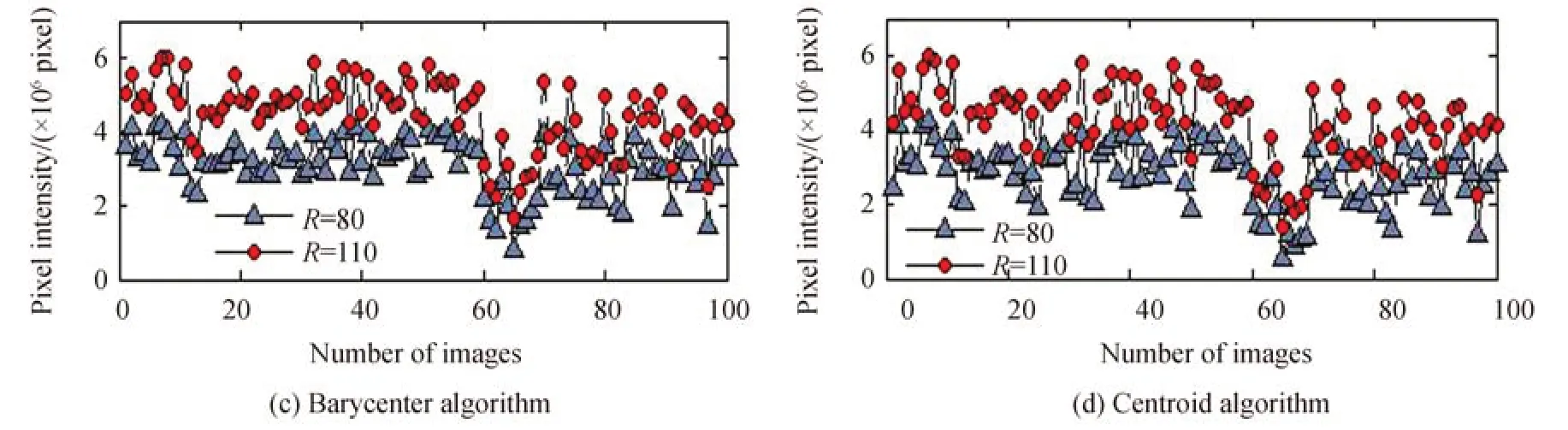
图14 不同算法下2.4 km 100 张光斑图像取不同半径掩膜内像素强度Fig.14 Intensity of the pixels in mask from 2.4 km spot image under different algorithms

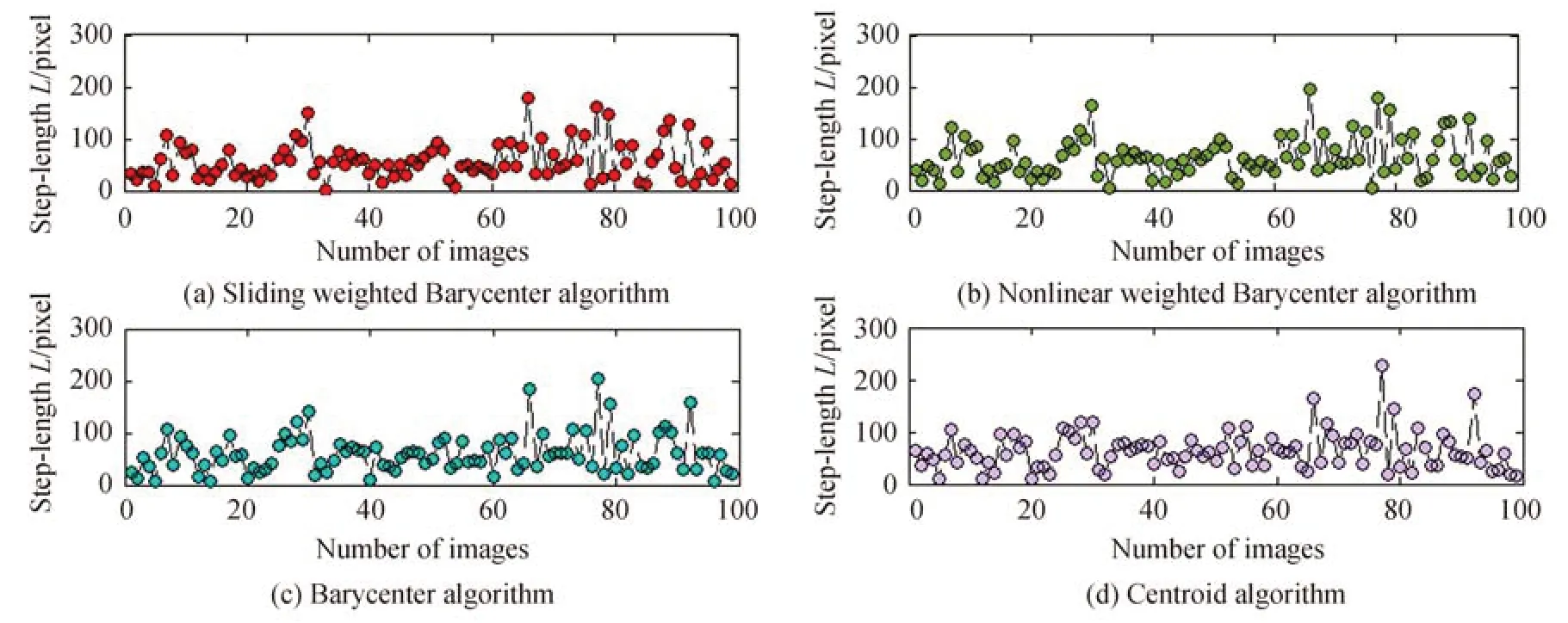
图15 不同算法下2.4 km 100 张光斑图像间定位间距Fig.15 Location distance between 2.4 km spot images based on different algorithms

定位算法持续定位连续光斑时，可以认为光斑定位中心强度越高以及连续图像定位的偏移步长越小，定位的效果越好。由于实验条件下得到的光斑是远距离激光传输，受湍流影响，光斑闪烁漂移甚至是破碎状态，在不知道光斑中心真值的情况下，实际定位中心间距将会远大于模拟环境下的值，但仍然保持在对应图像最小掩膜范围的中心区。

在表3 中，10.2 km 实验数据的结果中，SWB 算法的平均偏移步长最小，标准偏差相比BA、CA 法，虽在同一个数量级，但稍大。综合标准差与均值整体范围后，考虑此处的偏移情况，整体数据范围仍处于最低偏移范围，因此，相比其他三种方法，稳定性更好。表4 中，2.4 km 实验数据的结果中SWB 算法的平均偏移步长最小，其标准偏差较也最小，稳定性仍更好。由表3 和表4 中结果可得，在不同传输距离条件下，虽然NWB 算法的掩膜内像素强度优于其他三种算法，但连续光斑定位中心点的偏移步长最大，反映出稳定性较差。可以看出，提出的SWB 算法在不同湍流下连续光斑定位中心点的偏移步长最小，反映稳定性较好。在10.2 km 传输条件下，相比于NWB 法，连续光斑定位中心点的偏移步长最大可以减小9.9%，相比于BA 法，连续光斑定位中心点的偏移步长最大可以减小7.5%，相比于CA 法，连续光斑定位中心点的偏移步长最大可以减小11.7%；在2.4 km 传输条件下，相比于NWB 法，连续光斑定位中心点的偏移步长最大可以减小9.8%，相比于BA 法，连续光斑定位中心点的偏移步长最大可以减小5.5%，相比于CA 法，连续光斑定位中心点的偏移步长最大可以减小10.6%；而在掩膜内像素强度方面，SWB 法的像素强度不及NWB 算法，但仍优于传统的BA 法和CA 法。

表4 2.4 km 光斑处理过程效果分析Table 4 Effect analysis of 2.4 km spot processing

4 结论

本文提出了一种滑动加权质心定位算法，通过改进阈值分割方法，提高了光斑定位的精度，再通过对非线性权重质心定位算法加入滑动补偿机制，尽可能减小通信中由于光斑闪烁漂移带来的定位误差，提高了光斑定位稳定性和定位精度。通过模拟出高斯光束穿过大气湍流相位屏生成不同强度下畸变光斑，对滑动加权定位算法进行了理论验证，并由实验生成的连续光斑对算法进行了实验验证。结果表明，相比于传统的形、质心法、非线性权重质心定位法，本文提出的滑动加权质心定位算法对连续光斑间的定位步长有不同程度的减小，理论结果最大可以减小21.5%，实验结果表明对连续光斑定位中心点的偏移步长最大可以减小11.7%；且提出的滑动加权质心定位算法光斑中心掩膜内像素强度更高，因此综合定位效果更好。

可以看出，理论值的结果比实验结果定位出的效果好，一方面：文章主要为了验证在不同距离湍流强度下的光斑定位精度，因此在理论仿真光斑图像过程中，没有考虑平台的抖动等其他外界因素，因此理论生成的图像漂移程度比实验捕获的程度小，进一步导致滑动加权质心定位算法的定位步长的减小，算法间的差距明显；另一方面，理论仿真生成的连续光斑不随时间变化，且仿真得到的光斑图像是随机生成的，不能保证完全达到实际湍流状态，因此理论数据的效果优于实验数据得到的结果。最后，本部分结论是基于外场实验捕获的光斑图像，进行处理得出的结果，下一步作者会将算法应用于伺服步进电机，并进行外场实验，对几种算法进行进一步的对比验证。