基于电流偏差的永磁同步电机滑模电流解耦控制
曾小莉,王维庆,王海云
(新疆大学可再生能源发电与并网技术教育部工程研究中心,新疆乌鲁木齐 830047)
1 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)因其在扭矩、功率密度、以及能量转换效率等方面的优势而广泛应用于新能源汽车和工业伺服系统等高性能驱动场合[1-2].
在dq轴坐标上定子电压方程由电阻压降、耦合电压、反电动势构成.随着转速升高,耦合电压所占比重增加[3].当一个子系统发生动态变化都会对另外的子系统产生影响,延长系统的动态响应过程.虽然滞环控制实现简单且具有很好的动态性能,但是电流中含有大量的高频谐波,严重影响系统的动态性能[4].如果耦合分量不能得到较好的补偿,系统的动态性能会降低,尤其是在高速或低载波比情况下[5].为了降低耦合影响,提高解耦效果,改善系统的动态性能,近年来学界已经提出大量的解决方法.文献[6]引入电流反馈解耦控制(current feedback decoupling control,CFDC)方法,直接以反馈电流和转速为对象计算系统产生的耦合电压,再进行前馈补偿.此解耦方法结构简单、操作性强,但系统易受数字延迟控制和参数失配的影响.文献[7]采用内模控制(internal model control,IMC)电流解耦方法,通过内模结构实现dq轴子系统间耦合补偿,相比于CFDC,虽然解耦效果有所提升,但在电机工作频率附近引发明显的欠阻尼振荡,从而降低系统的解耦效果.文献[8]在内模结构控制的基础上引入滑模电流控制,不仅有效抑制内模控制产生的欠阻尼振荡,而且提高了系统因参数摄动和外在扰动的鲁棒性,但内模解耦控制结构在实际应用中较复杂.文献[9-10]采用双环PI控制实现电流解耦补偿,但各PI控制器之间参数影响较大.文献[11]采用复矢量电流解耦控制器,但其本质是内模结构控制,同样存在内模解耦控制难以解决的问题.文献[12]提出偏差解耦控制方法,虽然控制结构及其实际可操作性优于内模控制,但同样引发欠阻尼振荡.文献[13]以偏差解耦控制为基础引入扰动观测器的方法,在电感参数变化和电流耦合项等引发的扰动时,实现该扰动的观测和补偿,但线性扰动观测器的稳定性和鲁棒性较差.神经网络逆系统解耦控制[14]具有对参数摄动和负载扰动的强鲁棒性,但需要大量的试验样本数据,其工程应用性很难.滑模控制因其高鲁棒性而在近年来受到学者们广泛关注[15-17].文献[18]基于电压前馈控制中引入滑模控制(sliding mode control,SMC),虽然参数鲁棒性增强,但电流指令突变引发系统抖动.文献[19]设计仅在滑模阶段运动的全局滑模观测器,避免了趋近运动阶段,实现了转矩和励磁的解耦,保证了系统整个运动过程的鲁棒性,但是需要增加传感器对电压信号进行补偿.文献[20-21]提出使用SMC消除交流异步电动机dq轴的耦合项影响,保证整个运动过程的鲁棒性,但异步电机的耦合项占比很大,导致输出电压产生高频开关量,因此必须增加低通滤波器,而选择低通滤波器的带宽又需要权衡实验中控制器产生的电压光滑性和电流震荡程度.
综合上述问题,本文为了简化方法结构,同时考虑实验操作强,提出一种基于电流偏差的滑模解耦控制(sliding mode decoupled control based on current deviation,CD-SMC)方法.以电流偏差解耦补偿永磁同步电机模型中的耦合项;采用积分滑模控制,并且引入新的滑模控制函数,设计只在滑动模态阶段运动的控制律,保证系统在整个运动过程中都具有鲁棒性;SMC根据电流偏差解耦(current derivation decoupling,CDD)输出电压和电机解耦模型输出电流实现电流解耦控制.采用400 w的永磁同步电机拖动步进电机,进行CD-SMC控制策略验证,并和CFDC方法以及CDD控制方法进行对比.
2 传统电流解耦方法
2.1 永磁同步电机的数学模型
通常将两相旋转坐标d轴定向在转子磁链上,则同步旋转坐标系下永磁同步电机的数学模型为
式中:ud,uq分别为电机dq轴电压分量;id,iq分别为电机的dq轴电流分量;Ld,Lq分别为dq轴电感;ψf为永磁体的磁链;Rs为定子电阻;ωe为电机转子电角速度.
对于永磁同步电机,运行过程中使定子电流的d轴给定分量始终为0,则其电磁转矩Te的方程为
式中:Te为电磁转矩;Pn为极对数.
PMSM的运动方程为
式中:TL为负载转矩;J为电机的等效转动惯量;Bm为传动摩擦系数;ωm为转子机械角速度.
对PMSM的数学模型作拉氏变换,以描述电流环控制为
由式(4)看出,在定子电压方程中,对定子电流id,iq而言,永磁同步电机呈现为微分项的一阶滞后环节,电流环控制方程中存在dq轴的交叉耦合项.耦合项内含有转子转速项,其大小与同步频率成正比,在电机高速运行情况下系统耦合更加严重.如果不采取解耦措施,dq轴子系统的相互影响将会严重降低系统的动态性能.
2.2 电流反馈解耦控制
若实现PMSM耦合电流完全解耦,CFDC通过引入dq轴电流的耦合量作为补偿,进而解除交、直轴之间的耦合,实现电流的独立控制,电流反馈解耦控制结构框图如图1所示.其中G1(s),G2(s)依次为dq轴PI控制器传递函数,其以典型I型设计为被控对象的实际模型;图中Ld,Lq为控制器的使用参数值,其值可能与电机的真实参数不等.

图1 CFDC结构图Fig.1 Schematic diagram of CFDC
不考虑电流采样延迟,图1控制框图用传递函数表示为
由上式可以推出dq轴电流表达式为
式中:gdd1/Δ1和gqq1/Δ1分别为dq轴电流控制器的比例系数;gdq1/Δ1和gqd1/Δ1分别为dq轴电流控制器的耦合系数.
其中:
由式(7)耦合项系数可知,只有gdq1=gqd1=0,即控制器才能实现完全解耦补偿,即消除两子系统间的耦合项.但PMSM实际运行中因测量误差和运行条件的变化,当系统产生很大电流且电感值接近饱和时,电感值必然会发生变化,导致电感参数不匹配,使得解耦补偿项不能完全抵消永磁同步电机实际耦合项,从而影响系统的解耦效果和动态性能.图2给出了在电感参数失配情况下,即CFDC传递函数耦合项系数gdq1的伯德图.这里选择调节器的比例系数Kp=0.5,Ki=20.

图2 CFDC伯德图Fig.2 Bode diagram of CFDC
2.3 电流偏差解耦控制
CDD控制方式以给定电流值和反馈电流值的偏差量作为控制变量生成调节电压,同时引入解耦补偿项叠加在PI调节器生成调节电压上,以抵消永磁同步电机dq轴间实际耦合项,实现dq轴间的解耦控制.CDD原理如图3所示,图中G1(s),G2(s)分别对应d轴和q轴电流PI控制器的传递函数,G3(s),G4(s)为分别对应q轴和d轴解耦补偿项.
将图3写成传递函数形式为

图3 CDD结构图Fig.3 Schematic diagram of CDD
由式(10)看出,令gdq2=gqd2=0,可实现dq轴电流的完全解耦,于是得出
将式(11)中的Ld,Lq写成同时把解耦补偿项的输入变量移至PI控制器之后;在实际情况下忽略PMSM控制系统中定子电阻的变化对解耦控制的影响,可得出图4所示CDD控制器等效图.
由图4可知,式(10)中的各项参数为

图4 CDD等效图Fig.4 CDD diagram of equivalent block
图5给出了CDD耦合项系数的伯德图,CDD耦合项系数在400 HZ处产生谐振,谐振尖峰的出现使得其幅频增益从小于-50 dB的值增大至大于-50 dB,幅频增益的迅速变化会降低CDD控制器的解耦性能,并且伴随欠阻尼振荡的现象.

图5 CDD耦合项系数伯德图Fig.5 Bode diagram of CDD coupling
CDD系统中引入dq轴解耦项,会改变系统闭环传递函数零点和极点的分布位置,从而影响系统的动态性能.图6为CDD策略中系统零极点分布图和特定情况下的阶跃响应.图6(a)中,区域A为极点区,区域B为零极点混合区.区域B中的极点与部分零点构成偶极子.由于区域A中极点负实部的绝对值较小且区域B中未构成偶极子的剩余零点距离原点较近,相当于减小了闭环系统的阻尼,从而使其阶跃响应超调量加大.在图6(b)中,对应与区域B中距离虚轴最近的极点,其阶跃响应超调量较大但衰减速度较快;对应与区域B中距离虚轴最远的极点,此时阶跃响应超调量小但衰减速度较慢.不管哪种情况其阶跃响应曲线在进入稳态前都会出现振荡.

图6 CDD耦合传递函数零极点分布图和阶跃响应图Fig.6 Zero pole distribution and step response of CDD coupling transfer function
3 基于电流偏差的滑模电流解耦控制
3.1 非线性控制函数
传统的滑模面通常以开关函数sgn(H)作为控制函数,其优点为响应迅速,抗扰动性强,但因其函数的非线性开关特性而引起系统抖振,影响系统的鲁棒性,在很大程度上降低交直轴解耦效果.也有滑模面选取饱和函数sat(H)作为控制函数,在滑模运动阶段固有的线性开关特性仍会引起系统抖振,影响系统的鲁棒性.因此本文采用一种新的控制函数,其在滑模阶段呈非线性光滑特性,如下所示:
式中ε为边界层.
图7给出了sat和Z函数随误差变化的增益特性.

图7 2种控制函数的增益图Fig.7 Gain diagram of the two control functions
根据图7看出适当增大ε的值能降低滑模的抖振,如果选取ε值太大,又会使得系统的响应时间变长,影响解耦程度,降低系统的鲁棒性.因此选取合适的ε值,能更好消除系统受参数摄动和外在扰动的影响,提升系统的鲁棒性.
3.2 滑模电流解耦控制
在PMSM数学模型完全解耦的条件下,同时把耦合项的id,iq改写为时得出
实际情况下,因参数摄动和外在扰动等因素的影响,式(1)的模型等效为
式中:ΔLd,ΔLq,ΔRs,Δψf分别为参数Ld,Lq,Rs,ψf相对量;ξd,ξq作为多种外部扰动和未建模部分的总和.
若能找到合适的控制律u使dq轴运动保持一致,就能解决参数摄动和外在扰动影响的问题.因此,在偏差解耦控制器的输出端上叠加u,使u抵消影响因素f(x,τ),即u=f(x,τ).为此引入SMC控制策略,使其叠加在CDD控制器的输出端,使SMC的输出满足式(14)的要求,改善CDD解耦不完全的性能,同时提高系统的鲁棒性[22].因滑模控制器只有在滑动模态阶段具有对扰动的鲁棒性,工作在趋近阶段时不具备鲁棒性.若必须使整个运动过程工作在滑模阶段,则定义q轴电流滑模面为
将式(1)代入式(16),滑模面对时间t求导得
可以看出CDD电流调节器的补偿转子磁链与电机内的转子定向磁链相互抵消,消除因转子磁链定向在q轴产生的反电动势造成的耦合影响.
设计q轴滑模控制律为
选取Lyapunov函数分析系统的稳定性,即
对式(19)两边求导得
将式(17)带入式(20)得
由式(21)可知,当α>0,β>0时,满足,表明q轴电流滑模的存在性和可达性,系统即可实现滑模运动,就能保证在滑模运动阶段系统的稳定性和鲁棒性.
同理定义d轴电流的滑模面为
用同样理论判据可证明d轴电流滑模控制系统的稳定性,则d轴电流滑模控制律为
CD-SMC的控制框图如图8所示.

图8 CD-SMC原理图Fig.8 Schematic diagram of CD-SMC
图9为CD-SMC耦合传递函数的零极点分布图和特定情况下的阶跃响应.在图9(a)中,区域A为极点区,区域B为零极点混合区.由于区域A中极点负实部的绝对值较大,相当于增加了闭环系统阻尼,从而使其阶跃响应超调量减小,其响应分量衰减迅速.对比图6(b)和图9(b)可知,CD-SMC耦合传递函数阶跃响应超调量非常小,调节时间短,从而使响应曲线在进入稳态前无振荡现象,解决了CDD存在的问题.

图9 CD-SMC耦合传递函数零极点分布图和阶跃响应图Fig.9 ZeropoledistributionandstepresponseofCDSMC coupling transfer function
3.3 鲁棒性证明
系统运行过程中,切换函数H受参数摄动和外界扰动的干扰,则切换函数改写为
由李雅普诺夫理论判据可得
由式(25)可知,只要切换函数中满足条件α|xd|Ld>|fd|,就能证明˙V≤0成立,就能在参数摄动和外在扰动因素下确保滑模运动的不变性,提升整个系统的鲁棒性.同样,可以证明q轴电流滑模控制的鲁棒性.因此,本文提出的CD-SMC解耦方法在保证较好解耦能力,同时对PMSM具有较强的鲁棒性.
4 基于电流偏差的滑模电流解耦控制
4.1 非线性控制函数
为验证CFDC,CDD,CD-SMC 3种电流调节器解耦策略的有效性,用MATLAB/Simulink搭建PMSM仿真模型,在电感参数变化和负载转矩突增突减的情况下对3种方法进行了对比分析.永磁同步电机参数如表1所示,CD-SMC的系统结构图如图10所示.

表1 PMSM电机参数Table 1 Parameters of PMSM
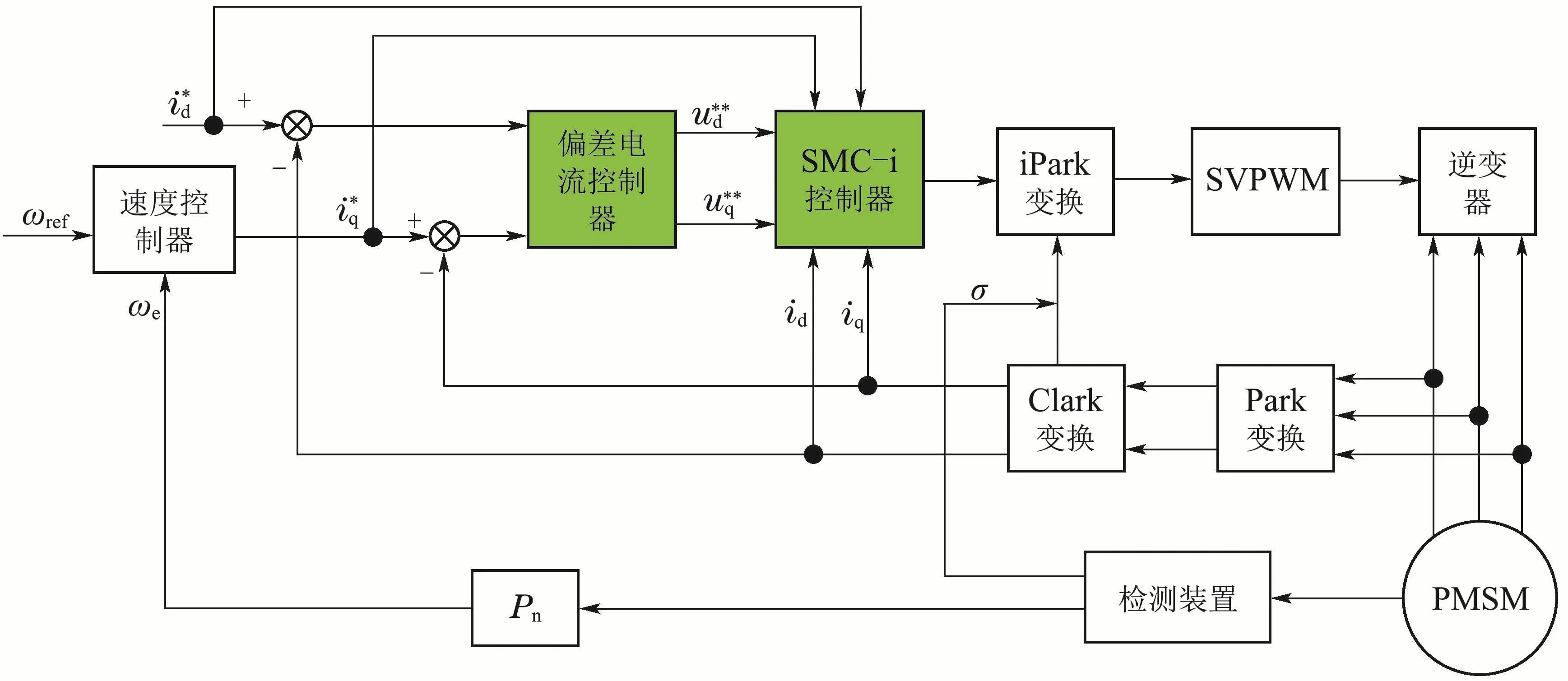
图10 CD-SMC的系统结构图Fig.10 Block diagram of control system of CD-SMC
4.2 负载转矩扰动下的电流响应
永磁同步电机设定转速为2000 r/min,给定初始负载转矩为3 N·m,在t=0.3 s时刻突增负载至6 N·m,在t=0.6 s时刻突减负载至3 N·m.由图11可知dq电流滑模运动轨迹从开始就处于滑模面上,避免了趋近运动阶段,保证了整个运动过程的鲁棒性.

图11 dq电流滑模运动轨迹Fig.11 The sliding trajectories ofdqaxis current
图12-14为不同解耦方法对dq轴电流变化的影响程度.永磁同步电机设定转速为2000 r/min,给定初始负载转矩为3 N·m,在t=0.3 s时刻突增负载至6 N·m,在t=0.6 s时刻突减负载至3 N·m.当电感参数失配时,dq电流相互影响,因动态解耦不完全产生不同程度的波形振荡.

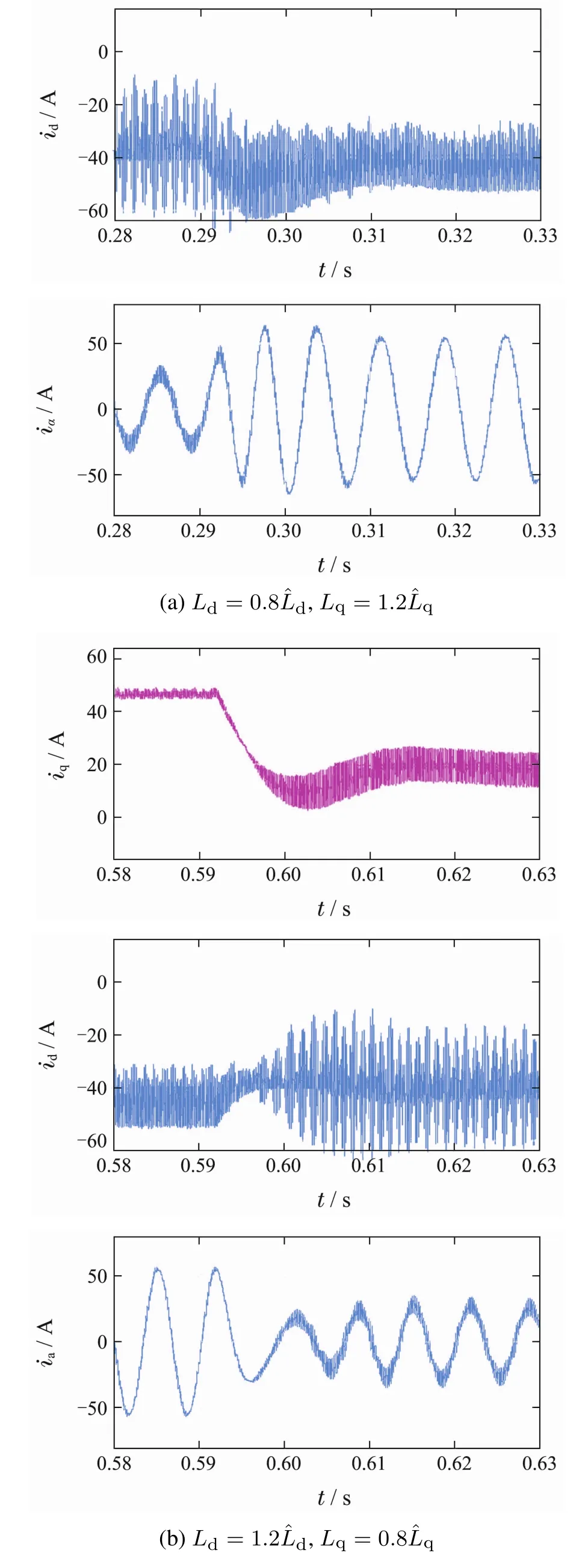
图12 采用CFDC的电流响应Fig.12 Current responses with CFDC
5 实验验证
以TI公司TMS320F28335为核心控制器,搭建相应的实验平台,验证基于电流偏差解耦控制的永磁同步电机滑模控制策略的控制效果.根据表1的电机参数搭建如图15所示的实验实物图,基于DSP的PMSM控制系统的硬件结构图如图16所示.采用400 W永磁同步电机,拖动型号为YH57BYGH56步进电机;DSP处理器中PWM开关频率设定为10 KHZ,直流母线电压由直流稳压电源输出,其大小设为30 V.以EPWM和RC滤波组合电路等效为数模(DA)转换芯片,将电流模拟信号输出给示波器.

图13 采用CDD的电流响应Fig.13 Current responses with CDD
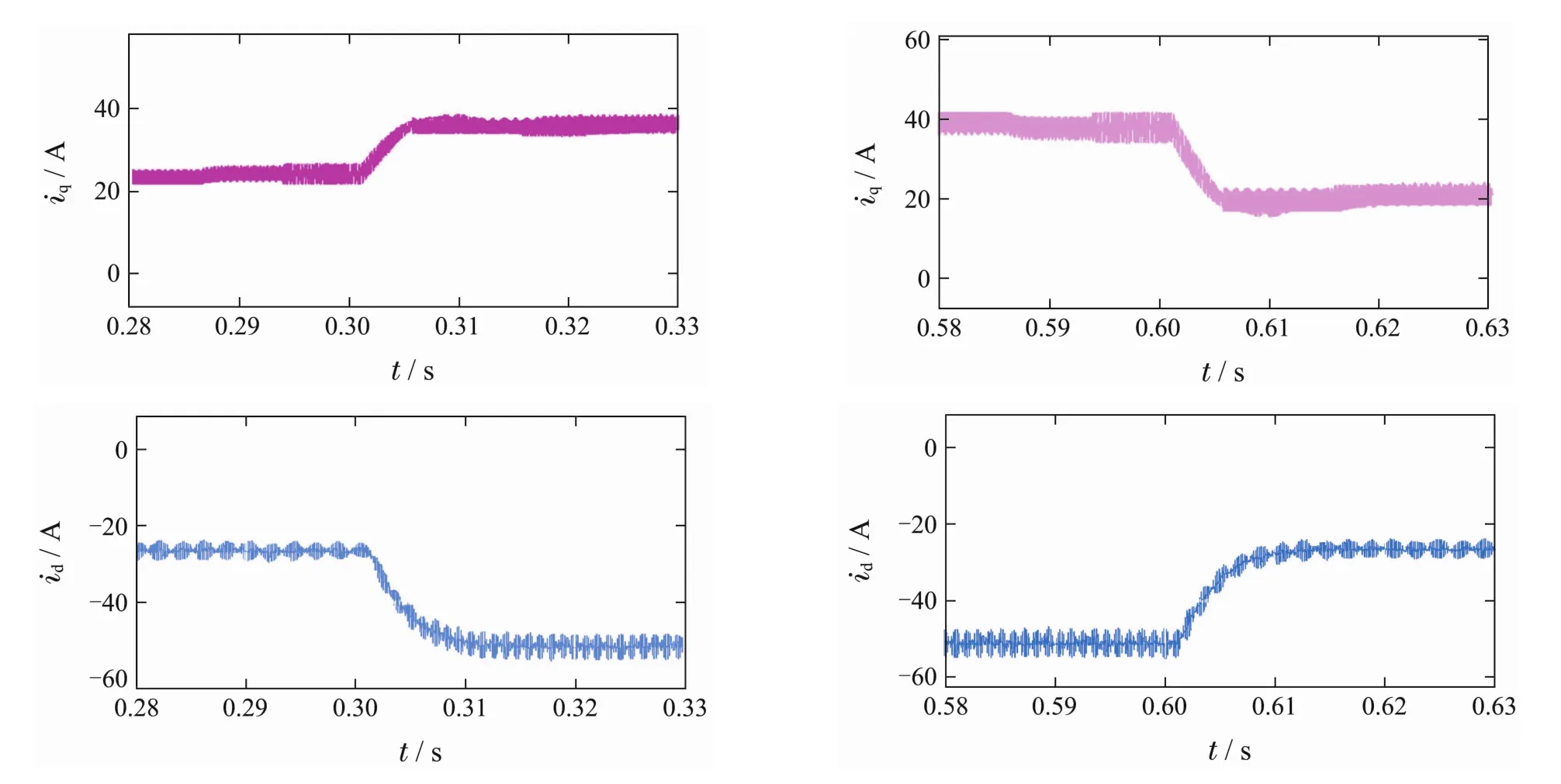

图14 采用CD-SMC的电流响应Fig.14 Current responses with CD-SMC

图15 实验平台实物图Fig.15 Experiment platform

图16 基于DSP的PMSM控制系统的硬件结构图Fig.16 Hardware frame map of PMSM control system based on DSP
由图17可知,d轴、q轴、a相电流产生扰动时,其响应恢复时间均需0.8 s.由图18可知,d轴响应恢复时间需0.56 s;q轴电流响应恢复时间需0.6 s;a相电流响应恢复时间需0.57 s.由图19可知,CD-SMC电流调节器d轴电流响应恢复时间需0.24 s;q轴电流响应恢复时间需0.28 s;a相电流响应恢复时间需0.24 s.表明CDSMC控制策略响应时间较CDD和CFDC快,其系统dq轴电流耦合较弱,克服了CDD振荡的缺点,并且对电感参数变化的鲁棒性较强.
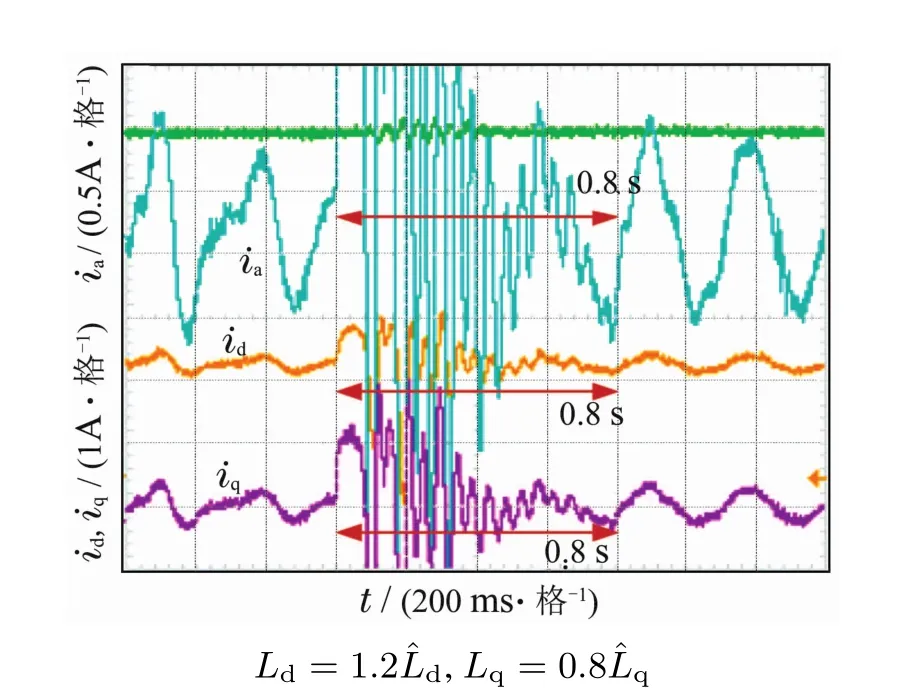
图17 CFDC电流响应时间Fig.17 Response time of CFDC current

图18 CDD电流响应时间Fig.18 Response time of CDD current

图19 CD-SMC电流响应时间Fig.19 Response time of CD-SMC current
6 结论
本文提出的CD-SMC控制策略,获得了较好的解耦性能和较强的鲁棒性.通过理论分析和实验对比,得到以下结论:
1)CFDC易受电感参数变化的影响,解耦效果对电机参数的依赖性较强.
2)CDD动态解耦效果优于CFDC,但在电机工作频率附近也引发欠阻尼振荡.
3)对SMC控制方法引入新的控制函数,设计滑模控制律,有效抑制系统抖振,保证系统仅在滑动模态运动,避免了趋近运动,使整个运动过程具有较强的鲁棒性.
4)采用CD-SMC控制方法,不仅保留了CDD较好解耦效果优势,且超调量小,改善了系统的动态性能和稳态性能.
5)采用CD-SMC控制方法响应时间短,交直轴电流耦合弱,参数鲁棒性强.
6)该控制策略应用于电动汽车驱动时,能有效提升汽车行驶中的动态性能.

