海流环境下多AUV多目标生物启发任务分配与路径规划算法
刘晨霞,朱大奇,2†,周 蓓,顾 伟
(1.上海海事大学智能海事搜救与水下机器人上海工程技术研究中心,上海 201306;2.上海理工大学机械工程学院,上海 200093)
1 引言
多自主式水下机器人(autonomous underwater vehicle,AUV)系统的任务分配与路径规划是指在复杂且多变的海洋环境中合理地分配水下作业任务给一组AUV,同时使每个获得任务的AUV都能规划出一条无碰撞且消耗能源最少的路径.多AUV系统多目标任务分配与路径规划在海底资源探索、军事侦查、水下搜救等方面有广泛应用前景,是近年来海洋工程领域的研究热点.
目前,任务分配方法研究主要分为3大类:基于行为的任务分配方法、基于市场竞争机制的任务分配方法和主从式任务分配方法.典型的研究成果如早期M.J.Mataric和L.Parker[1-2]提出基于人类社会行为的多AUV任务分配算法,主要是模仿人类工作的跟踪、传播、集成、命令的过程进行任务分配与路径规划;90年代后期,R.Akkiraju和R.Turner[3-4]等提出基于市场竞争机制的多AUV任务分配策略,它的基本原理是最小成本付出最大效益收获的市场竞争规则;近期S.Yoon[5]等针对多AUV水下搜索任务分配问题,首先指定一个主AUV,由它与水面母船通信交换信息,其他AUV与邻近AUV采用等待方式依次交流信息,最后将水下搜救及机器人自身信息传输到主AUV,由主AUV集中处理,并以邻近传递的方式发送命令给其他AUV系统,以多AUV编队形式完成水下全覆盖协作搜寻.
上述任务分配方法均假定水下环境已知且静态不变的,并以此为依据建立水下任务分配或跟踪围捕模型,虽然能够进行多AUV任务分配,简化了跟踪围捕方法的难度,但这种已知的静态模型与实际的水下环境存在相当大的距离.在实际水下作业中,AUV位置是不断变化的,同时海流的大小对AUV的运动影响也较大,因此,多AUV任务分配是一个动态多次分配过程,而不是一次性静态分配过程;另外,上述AUV任务分配方法大多只研究分配问题,未讨论水下机器人路径规划.由于任务分配与路径规划问题相互耦合,规划以分配为基础,分配又直接受规划结果的影响,仅仅研究任务分配而回避路径规划,其结果难以满足实际作业需要.因此,不仅需要探索复杂水下环境下动态任务分配方法,而且需要进一步研究多AUV任务分配与路径规划的集成与关联.
近年来,许多研究者将多传感器信息融合、人工神经网络等智能信息处理算法引入到多AUV任务分配与路径规划研究中.典型的研究成果如B.Chow[6]提出一个改进的K-均值算法,用来解决常值海流环境下的多AUV系统任务分配和路径规划问题,这个算法通过Dubins模型、AUV动态模型以及海流模型的结合,综合考虑多水下机器人系统的任务分配与路径规划问题.但是,该算法存在的问题是:K-均值在完成多任务作业时,对移动目标物不敏感,另外,算法仅研究了二维海流模型和无障碍物的水下环境,对实际的多障碍物水下环境来说,降低了算法的难度与适用性.
J.J.Ni[7]等将生物启发神经网络模型引入多地面移动机器人协作围捕中,提出多机器人智能围捕、自动避障策略,并给出了二维平面上机器人搜索、避障追踪、合作围捕的仿真结果,但该算法仍然假设所有移动机器人能无条件感知逃逸目标和障碍物,与实际环境和机器智能仍有较大差距,也没有考虑机器人的运动约束问题.
受任务分配与自组织神经网络原理相似性的启发,近些年来有学者将自组织神经网络(self-organizing map,SOM)模型应用到多机器人任务分配与路径规划研究中.H.Huang[8-9]等利用SOM神经网络的自组织竞争实现多任务自适应动态分配,通过获胜神经元的权值更新实现AUV的路径规划,未考虑三维的水下实际环境和AUV的运动能力.对此D.Q.Zhu[10-11]将水下环境地图与SOM任务分配算法结合,进一步考虑AUV实际运动能力问题(每次仅航行一个地图单元),提出一种新的集成多AUV自组织任务分配与路径规划算法,使得多AUV任务分配与规划方法更接近实际情况,但该方法是通过目标物与AUV之间的欧式直线距离大小来分配任务,无法适应障碍物环境的任务分配.M.Z.Chen[12-14]等将生物启发神经网络与SOM模型结合,设计了一种新的任务分配与路径规划算法,应用SOM自组织性质进行任务分配,应用生物启发模型自适应输出机制实现安全避障,但没有考虑水下环境中海流的实际影响,与水下现实环境仍有一定差距.
本文聚焦水下多障碍物与海流环境,提出一种生物启发神经网络与速度矢量合成的自主任务分配与路径规划算法.将生物启发神经网络(biologically inspired neural network,BINN)中的每一个神经元与水下环境栅格地图中的位置单元一一对应,计算比较每个目标物在BINN地图中所有AUV的活性值,并选取某个目标物中活性值最大的AUV作为它的获胜AUV,实现多AUV任务分配;针对常值海流的影响,利用矢量合成算法确定AUV实际的航行方向,实现AUV路径规划与避障.
2 多AUV多目标生物启发自主任务分配与路径规划算法
多AUV系统的任务分配与路径规划是指在多障碍物水下环境中合理地分配水下作业任务给一组AUV,同时使每个获得任务的AUV都能规划出一条无碰撞的最短路径.为了完成对工作环境中所有目标的访问,将每个任务目标分配给不同的AUV,AUV在得到目标任务后进行路径规划,自主航行到任务目标点,保证AUV航行路径最短,同时满足AUV航行速度的运动学约束和安全避障.本文提出的多AUV多目标生物启发自主任务分配与路径规划算法,包括4部分内容:一是水下环境的BINN建模;二是基于BINN模型的多目标任务分配;三是基于BINN模型的AUV自主路径规划与避障;四是AUV海流环境下路径规划.流程图如图1所示.
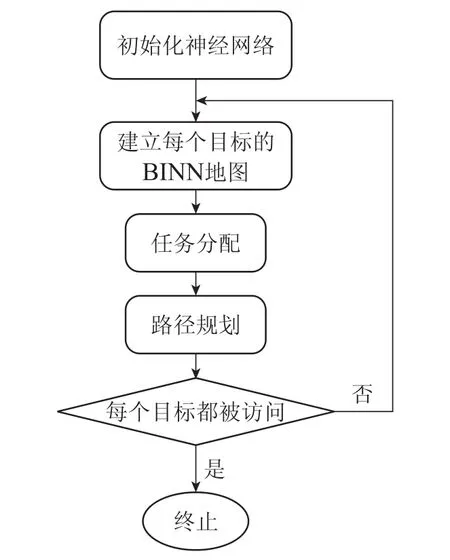
图1 生物启发自主任务分配与路径规划算法流程Fig.1 Biologically inspired autonomous task assignment and path planning algorithm flow
2.1 BINN算法数学模型
在水下环境栅格地图的基础上,建立生物启发神经网络模型,用该模型表示AUV工作环境,神经网络中的每一个神经元与栅格地图中的位置单元一一对应,如图2所示,根据神经网络中神经元的在线活性输出值分布情况,确定目标任务分配给哪个AUV,且使AUV自主规划出一条无碰撞且节省能量的航行路径.
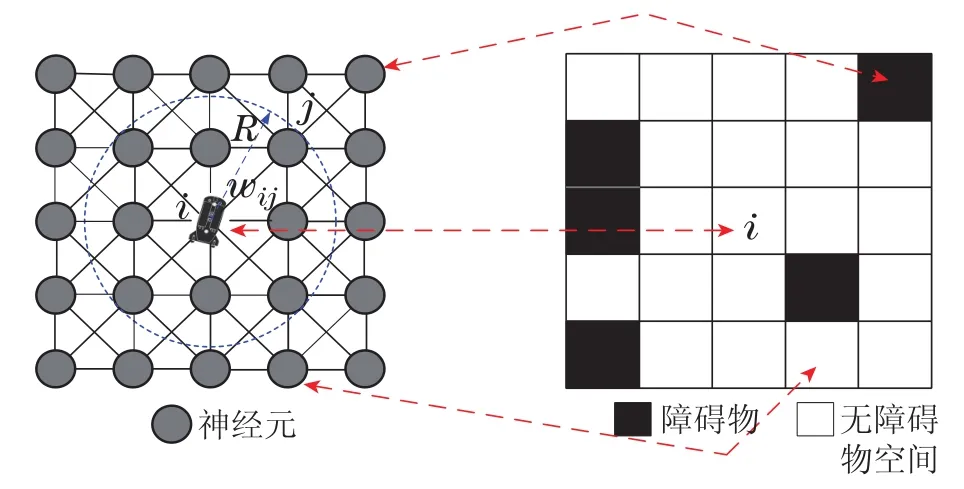
图2 二维生物启发神经网络与环境地图映射Fig.2 Mapping between two dimensional biologically inspired neural network and environmental map
本文中BINN[15-16]算法是一种离散的生物启发神经网络,它的基本思想是目标不断向外传递激励,而障碍物则对激励有抑制作用,通过迭代计算出每个位置的活性值.BINN模型具有记忆特性,也就是说从地图上的任何一点都可以通过不断迭代求解回到激励发出点,也就是路径规划问题中的目标点.BINN模型数学描述如下:
其中:vi代表神经元i的输出活性值,w是连接系数矩阵,它的网络结构如图2所示,由它的网络结构易知接系数矩阵w是一个对称的矩阵.wij表示第i个神经元与第j个神经元之间连接系数.|qi-qj|表示第i个神经元与第j个神经元之间欧式距离,A,B,D是正常数,A代表第i个神经元活性值的衰减率,B和D第i个神经元活性值的上限与下限,vi∈[-D,B].[Ii]++是激励输入,[Ii]-是外部抑制输入,[Ii]+的数值是max{[Ii,0]},[Ii]-的数值min{[Ii,0]},Ii的数值由式(3)计算,由地图栅格单元性质决定.R表示与第i个神经元链接的神经元数量,二维为8,三维为26.
外部输入信号由障碍物与目标物产生,从式(1)-(3)可以看出,神经元输入激励主要来自于外部目标激励与内部神经元之间的活性值;神经元的输入抑制主要来自外部障碍物.当Ii≤0时,神经元的激励信号主要来源是内部传递的活性值,由此可见生物启发神经网络中目标物具有全局吸引,而障碍物只有局部抑制.
2.2 基于BINN的多目标任务分配算法
多目标物的任务分配问题可以拆分成多个单目标物的问题.目标物的BINN地图是指将一个目标物作为神经网络的输入神经元,所有的AUV作为输出神经元,然后利用生物启发式动力学模型计算出栅格地图中各个位置的活性值.因此,可以得到每个目标物的BINN地图中活性值最大的AUV.如果多个目标物将同一个AUV作为获胜AUV,则需要比较分析该AUV在这几个目标物的BINN地图中的活性值,AUV在哪个目标物的BINN地图中活性值最大就视作是哪个目标物的获胜AUV.式(4)中的矩阵V表示的是每个目标物的BINN地图中的所有AUV的活性值.利用式(5)可以选择出每个目标物的BINN地图中活性值最大的AUV.
其中:m表示目标物的数量,n表示AUV的数量.vij表示为目标i(i=1,2,···,m)的BINN地图中第j(j=1,2,···,n)个AUV所处位置的活性值,定义vimax是矩阵V中第i行的最大值.也就是说,与其他AUV相比,第i个目标物的BINN地图中第imax个AUV具有最高的活性值.
整个任务分配过程如下:
1)利用式(1)-(3)计算每个目标物的BINN地图中所有AUV的活性值vij(i=1,2···,m;j=1,2,···,n);
2)矩阵第i行的最大值是位于第imax列的viimax,第k行的最大值是位于第kmax列的vkkmax,其中i和k的值不相等.表示第i(i=1,2,···,m)个目标在BINN地图中第imax个AUV活性值最大,第k(k=1,2,···,m)个目标在BINN地图中的第kmax个AUV活性值最大.
2.3 海流环境下AUV路径规划的BINN算法
对获得具体目标任务的AUV来说,需要针对水下多障碍物与海流环境,规划一条从AUV起始点到目标点的无碰最优航行路径.障碍物对路径规划的影响主要是规划的路径不能穿过障碍物,而海流对路径规划的影响主要是在海流影响下如何使得AUV能够沿着预设的最优路径行驶.
2.3.1 生物启发AUV路径规划与安全避障
对于路径规划与安全避障问题,将AUV的运动路径进行离散化,路径规划问题演变为寻找AUV的下一个行驶位置,只有准确找出该位置,才能使AUV自主规划出一条无碰撞的行驶路径.具体来说,AUV进行路径选择时,先根据式(1)-(3)计算当前位置周围所有神经元的输出值,然后选择周围输出最大的单元作为下一步的航行选择,到达下一位置后再如此反复执行,直到最终完成所有待搜索单元的访问.由于障碍物单元的抑制作用,其对应神经元输出小,目标单元对神经元输入激励作用,其对应神经元输出大,AUV根据神经元输出大小,朝着输出最大的临近地图单元航行,从而自适应地避开障碍物,到达目标单元,实现AUV路径规划与安全航行.
2.3.2 海流环境下生物启发AUV路径规划
深水海流对水下机器人路径规划的影响,可以通过海流模型进行补偿.海流是海水相对稳定的非周期性流动,随季节、气候、海域、地形、深度变化而变化,是时间和空间的复杂函数,目前很难用精确的数学表达式描述其运动规律.但海流随时间和空间的变化是在较大范围内发生的,而在有限的特定海域和特定时间段内,特别是深海水下机器人的深海环境,海流的强度(流速)和流向都是比较稳定的;同时考虑水下机器人的航行能力有限,只能在特定的时间段和海域内作一定距离航行,因此,可将海流的运动简化为变化较缓慢的流动,即考虑海流的流速与方向.
海流对路径规划的影响主要是在海流影响下如何使得AUV能够沿着预设的最优路径行驶.此处引入矢量合成算法来解决,主要是通过海流速度与AUV预设航行速度合成,使其合成速度方向保持在规划的方向上,如图3显示的是AUV在海流影响下运动方向的变化情况.在常值海流的影响下,AUV的行驶方向与海流的方向通过矢量合成得到AUV的实际移动方向;对时变海流环境下,可以看作不同常值海流的组合,在特定的时间段和海域内可以将海流当作流速与方向一定的常值海流处理.
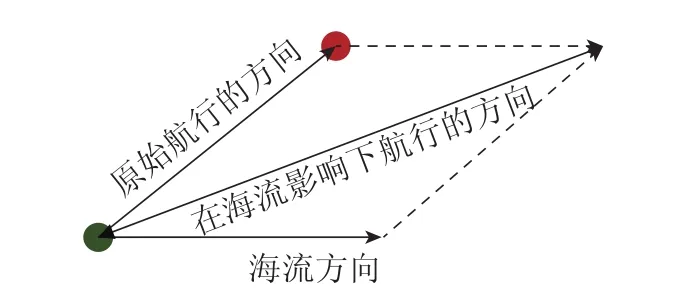
图3 在海流影响下矢量合成Fig.3 Vector synthesis under the in fluence of ocean currents
AUV在行驶过程中受海流的影响会偏离既定的航道,为了使AUV按照原来的航线前进,引入方向信度加权算法将海流对AUV路径选择的影响尽量降低.该算法的核心思想是在计算AUV邻域的活性值时减去海流对AUV转向矢量的影响,在消除海流的影响之后,再比较活性值的大小从而选择AUV的最优路径.AUV的路径选择如式(6)所示:
其中:vij表示的是第i个AUV的第j个邻域位置处的活性值,其中R在二维环境下的值小于等于8,在三维环境下的值小于等于26.k在[0,1]范围内取值,本文中k为0.05,用来控制海流对AUV转向矢量的影响程度.Pp是AUV的上一步的坐标位置,Pc是AUV的当前坐标位置,Pn是AUV的下一坐标位置,yj表示的是在海流作用下,AUV所产生的的转向矢量,它是一个与AUV艏向角度有关的函数,具体的表达式为式(7).式(7)中的Δθ是θ和φl之间的差值绝对值,定义为式(8).θ表示的是无海流情况下AUV的转向角度,定义为式(9).φl表示的是有海流情况下AUV的转向角度,定义为式(10).其中转向角度表示的是与x轴方向的夹角.
其中(xPc,yPc)和(xPn,yPn)分别表示的是无海流环境下AUV所处的当前位置坐标以及下一位置的坐标.(xPl,yPl)表示的是在有海流环境下AUV下一位置的坐标.
图4所示的是在海流环境下AUV的转向图.如果海流的方向与AUV原始的行驶方向一致时,即Δθ的值为0时,此时海流对AUV的行驶方向没有产生影响.如果海流的方向与AUV的行驶方向是完全相反的,即Δθ的值为180°时,则AUV在行驶的过程会受到海流反向作用力的影响.利用方向决策算法中的系数k将海流的影响进行了削减,使得AUV行驶的方向能够朝着既定方向前进而不发生偏移.因此,方向决策算法不仅可以帮助AUV系统在海流环境下能完成预定的任务,而且能够消除海流的影响,节约能源损耗.
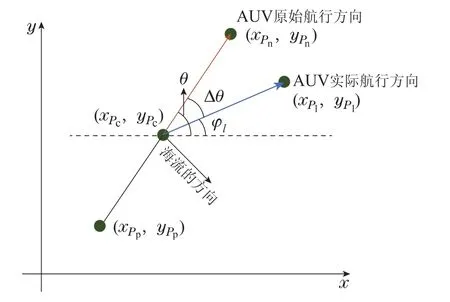
图4 AUV在海流影响下的转向Fig.4 AUV steering under the in fluence of ocean currents
3 实验仿真与分析
本文通过栅格法将环境地图离散化,将环境中包含障碍物的区域设置为障碍栅格,其他的设置自由栅格.符号T表示仿真环境中的目标,符号R表示AUV,仿真图中的红色圆点是目标、绿色圆点是AUV、蓝色连线是AUV的规划路径,黑色方块代表障碍物;BINN模型的控制参数见表1.为了表明BINN模型运用于AUV路径规划与安全避障中的可行性和有效性,在MATLAB 2016b中针对障碍物环境、海流环境进行任务分配与路径规划仿真实验.

表1 算法控制参数Table 1 Algorithm control parameters
3.1 45°海流环境下任务分配与路径规划

图5 AUV系统在45°常值海流环境下的初始状态Fig.5 Initial state of AUV system in45°constant current environment
应用式(1)-(4)计算每个目标物的BINN地图中活性值,比较T1在BINN地图中的R1,R2,R3和R4的活性值,发现R3在T1的BINN地图中具有最大的活性值,因此,R3作为目标T1的获选AUV;通过比较目标T2在BINN地图中R2的活性值最大,因此R2是目标T2的获选AUV;R4在T3和T4的BINN地图中具有最大的活性值,因此,R4作为目标T3和T4的获选AUV.最终,R3分配给T1,R2分配给T2,R4分配给T3和T4,R1未分配目标.所有目标都有了相应的获胜AUV,即T1-R3,T2-R2,T3-R4,T4-R4.
为了验证方向决策算法对消除海流影响是可行且有效的,图6和图7分别显示的是未添加方向决策算法和添加了该算法的实验结果图.通过对比发现,虽然存在方向和速度固定的常值海流,两者均能合理地分配AUV系统且能为每个AUV规划出一条无碰撞且无速度跳变的路径,但是可以明显发现AUV在未使用方向决策算法时受海流的影响相对较大,导致AUV系统行驶的距离有较大增加.如图6所示,在未使用方向决策算法的情况下,以R3为例,它为了绕开障碍物到达目标物T1,R3本可以向轴的正向行驶,但是由于45°的海流作用,AUV偏离了原来的航向,导致R3需要航行更远的距离才能够到达目标物T1;R4同样受到海流的影响使得它的路线发生了偏移,增加了R4航行到目标物T4的距离.
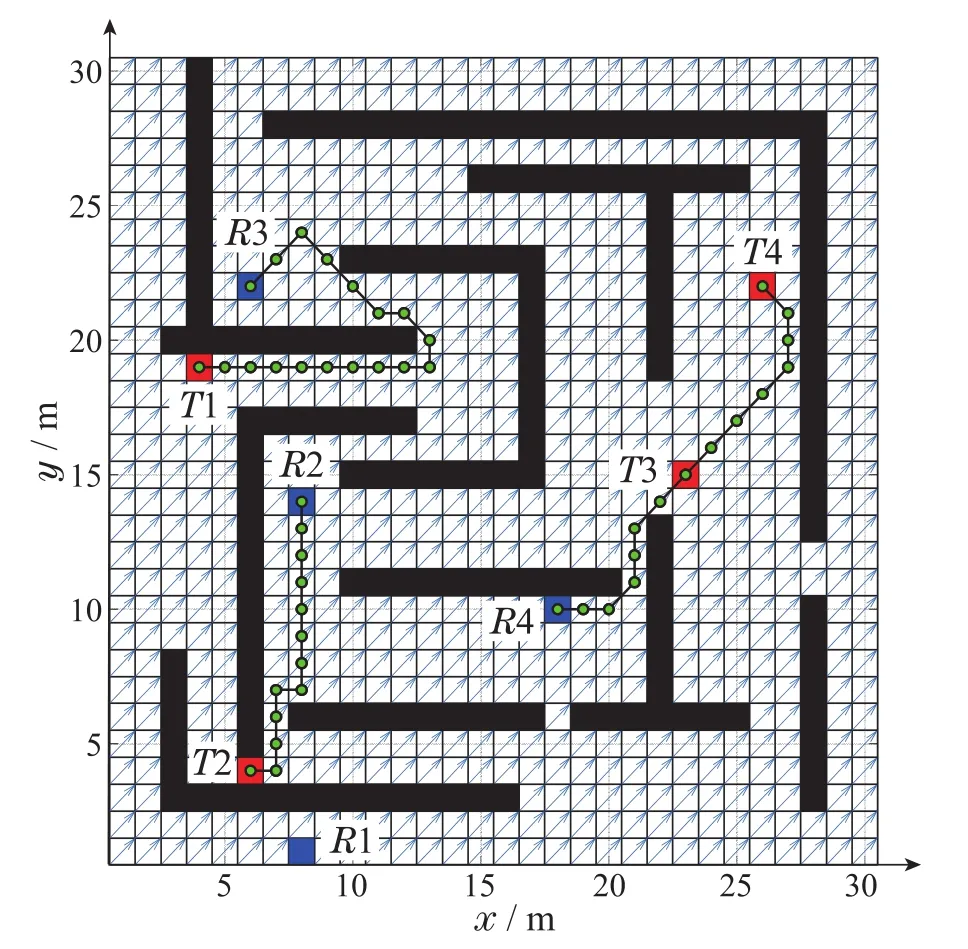
图6 无方向决策算法任务分配与路径规划Fig.6 Task assignment and path planning without direction decision making algorithm
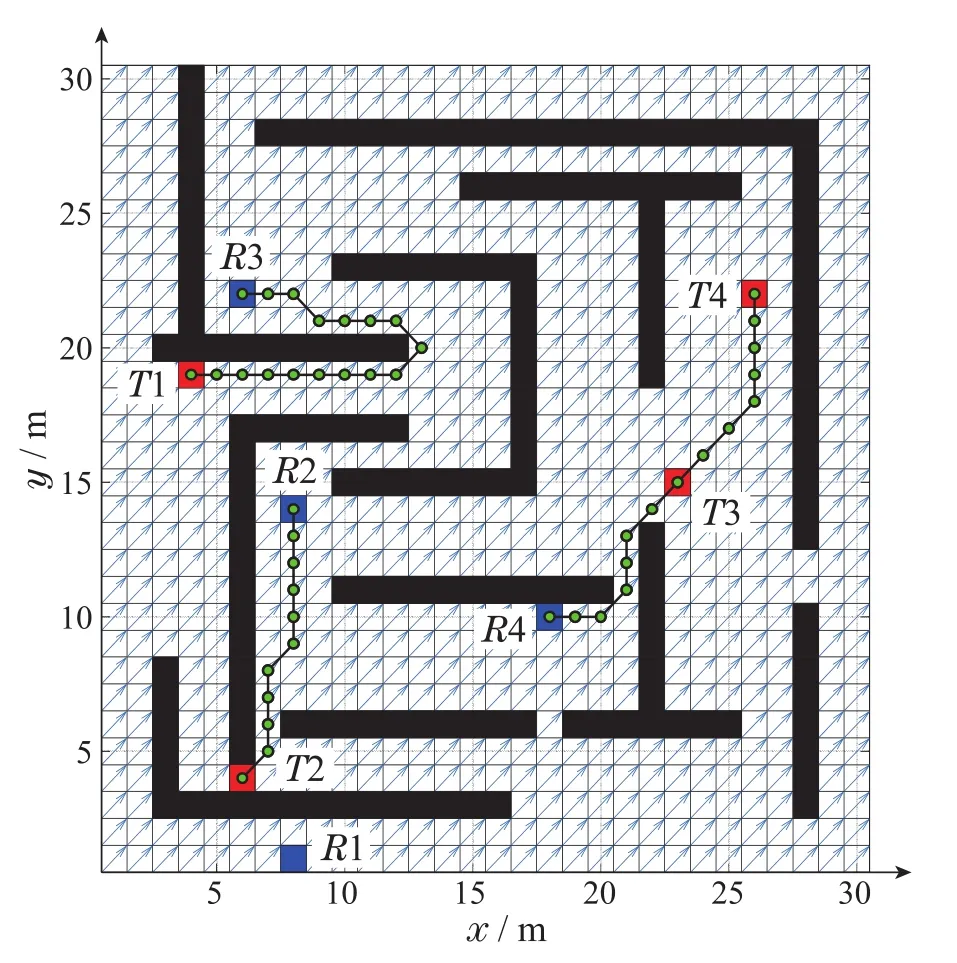
图7 有方向决策算法任务分配与路径规划Fig.7 Task assignment and path planning with direction decision making algorithm
而加入了方向决策算法之后,如图7所示,在生物启发神经网络模型的活性值计算中将海流的影响尽量降低,速度合成以后各个AUV能够沿着最优的路径到达对应的目标物.图8显示的是存在方向为45°常值海流的场景下,未使用方向决策算法与使用方向决策算法的各个AUV实际航行距离对比柱形图.可以发现,虽然未使用方向决策算法的多AUV系统也能够到达对应目标物的位置,但是各个AUV的行驶距离却有所增加.在完成整个任务后,未使用方向决策算法的AUV系统总距离为48.799 m,而使用了方向决策算法AUV系统的总距离为44.5563 m,减少了8.7%.上述情况可以证明使用方向决策算法能够有效消除海流对多AUV系统路径偏移的影响.

图8 常值海流下是否使用方向决策的距离对比Fig.8 Comparison of the distance made by direction decision making algorithm in45°constant current environment
3.2 180°海流环境下任务分配与路径规划
为了验证不同方向海流的影响,设计海流方向为180°,强度为栅格每秒,进一步研究海流对AUV规划航行的影响.初始状态和图5相同,有4个目标需要4个AUV去访问,4个AUV的初始坐标分别是R1(8,1),R2(8,14),R3(6,22),R4(18,10),4个目标物的坐标分别是T1(4,19),T2(6,4),T3(23,15),T4(26,22).
通过对比未使用方向决策算法和使用方向决策算法的仿真实验图,同样说明了方向决策算法的有效性.图9是未使用方向决策算法的仿真结果图.可以看出,水下环境中充满了与x轴正向呈180°的蓝色箭头,表示的是常值海流.图中4个蓝色方块表示的是4个AUV,4个红色方块表示的是目标物.绿色的圆点表示的是AUV行驶到对应目标物的路线.
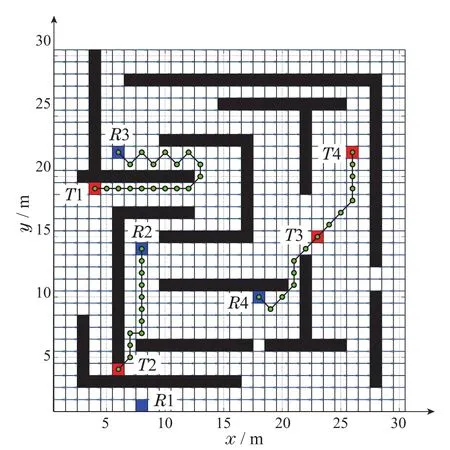
图9 无方向决策算法任务分配与路径规划Fig.9 Task assignment and path planning without direction decision making algorithm
图10是结合了方向决策算法的仿真结果图.对两种仿真实验结果图进行分析比较,以R3这个AUV为例,可以发现在不加入方向决策算法时,海流对其路径选择影响比较大,航行路线呈锯齿状,增加了R3到目标物T1的距离.而使用方向决策算法则会减弱海流对AUV航行方向的副作用,R3没有行驶多余的距离,减少了能源的损耗.而对于R4这个AUV,在避开障碍物的时候受到海流的影响,它的路线就会发生了偏移,但是在使用方向决策算法修正AUV邻域的活性值后,R4可以更加高效地完成任务.
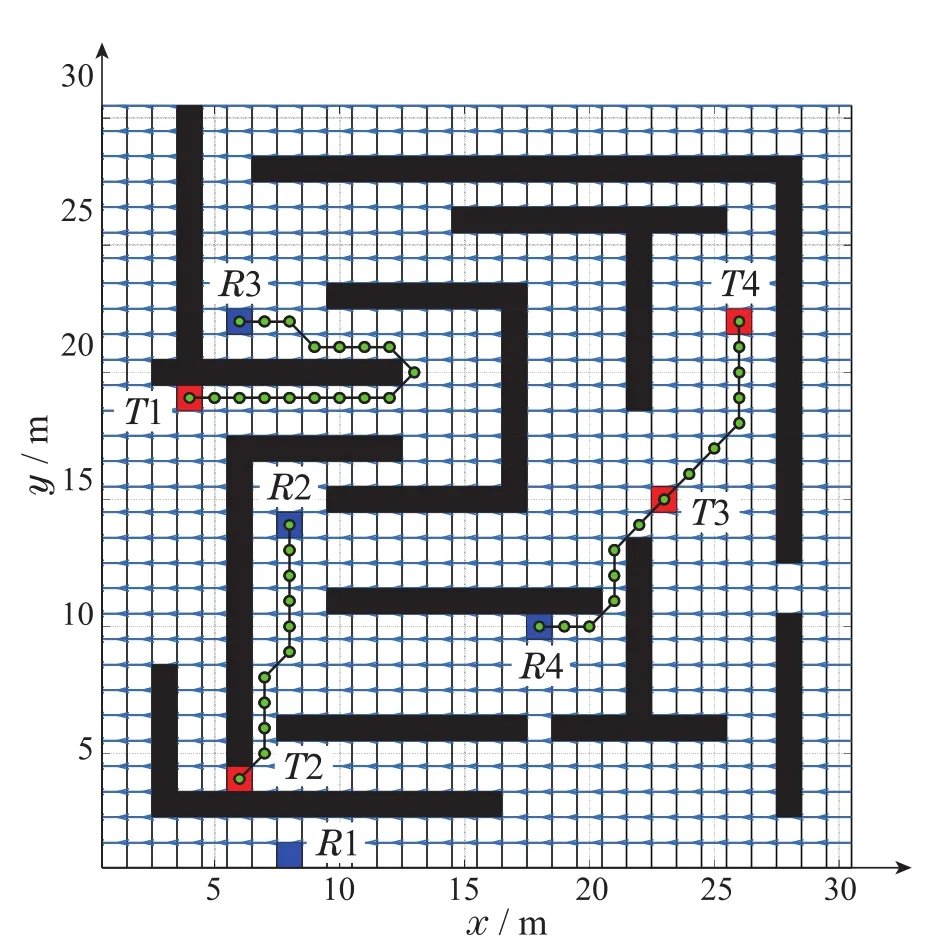
图10 有方向决策算法任务分配与路径规划Fig.10 Task assignment and path planning with direction decision making algorithm
图11显示的是存在方向为180°海流场景下是否使用方向决策算法的实际航行距离对比柱形图.从图中可以发现AUV系统在未使用方向决策算法时行驶的总路程49.0416 m,而在使用了方向决策算法总路程为44.5563 m,总路程减少了9.15%.海流的影响使得AUV行驶的方向发生偏移,所以AUV系统为了避开障碍物以及克服海流的阻力会调整整体的航行方向,导致航行距离有所增加.但是加入方向决策算法之后,削减了海流影响,AUV系统就可以规划出更加优化、消耗能量更少的路径.

图11 180°常值海流下是否使用方向决策的距离对比Fig.11 Comparison of the distance made by direction decision making algorithm in180°constant current environment
4 结论
本文在已经构建好AUV水下栅格地图的基础上,应用BINN模型研究多AUV多目标的自主任务分配与路径规划.该模型结构简单、无需样本学习与训练,使得多AUV得任务分配更合理,路径规划更高效.为了消除海流对AUV航行方向的影响,结合方向决策算法削减了海流的影响,AUV行驶的方向能够和无海流时的方向保持一致,减少了海流对AUV系统的能源损耗.

