高等数学视角下的高考概率统计题的背景分析与研究

张本红

(青岛中学)

高考概率统计解答题的出题背景越来越复杂,目前对高考数学试题的研究较多,但对高考试题出题背景的研究较少,尤其是对概率统计出题背景的研究.笔者以2019年高考数学全国Ⅰ卷理科第21题为例,从马氏链、差分方程等高等数学的视角出发,对高考概率统计题的试题背景进行分析,并给出一个典型例题,便于读者进一步研究.

1 试题回顾

题目 为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得－1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得－1分;若都治愈或都未治愈,则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.

(1)求X的分布列;

(2)若甲药、乙药在试验开始时都赋予4 分,pi(i＝0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0＝0,p8＝1,pi＝api－1＋bpi＋cpi＋1(i＝1,2,…,7),其中a＝P(X＝－1),b＝P(X＝0),c＝P(X＝1).假设α＝0.5,β＝0.8.

(ⅰ)证明:{pi＋1－pi}(i＝0,1,…,7)为等比数列;

(ⅱ)求p4,并根据p4的值解释这种试验方案的合理性.

2 试题背景分析与研究

事实上,用Xn表示甲药在第n轮试验中的得分,

其中fn＝(0,0,0,1,0,0,0,0).

根据题设给出的信息,可以得出条件概率即该马氏链的转移概率为

公式①从高等数学视角给出了关于pi的递推公式.

在实际试验的研究过程中,要进行成本控制,控制试验进行的次数,用Tk＝infn{n|Ym＋n＝8,Ym＝k}表示甲药的累计得分为k时转移至吸收状态,即试验结束时进行的试验次数,令τk＝E(Tk),即为此次动物试验的平均次数.由离散随机变量的期望,有如下递推公式:

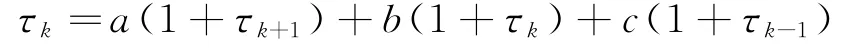
由边际条件得τ0＝τ8＝0.

公式②的含义是对试验的平均次数而言,甲药从累计得分为k转移至8,会比下一次试验后再转移至8分多一次.在下一次试验中,甲药分别以概率a,b,c得1分、得0 分、得－1 分,如果甲药的累计得分为k＋1,那么到试验结束时进行的试验次数为1＋τk＋1;如果甲药的累计得分为k,那么到试验结束时进行的试验次数为1＋τk;如果甲药得－1 分,累计得分为k－1,那么到试验结束时进行的试验次数为1＋τk－1.

由公式②得非齐次线性差分方程

以高等数学知识为背景命制的试题往往新颖创新,学生如果没有系统学习过高等数学,很难辨别试题的真实背景.然而此类试题的解答不会超过学生的认知,结合基础的概念、性质、法则等,考查学生用初等方法解决问题的能力.通过高等数学初等化的方式,还可以考查学生是否具备进一步学习高等数学的潜质,体现了高考的选拔性、创新性和导向性.

3 典型例题

数学学习离不开解题,当前中学数学的解题教学常常出现“题海战术”,但这未必有利于学生思维迁移性和延展性的发展.学生面对新颖的题目时,可能会出现束手无策的情况.教师应当以深厚的知识储备和敏锐的洞察力精选试题,深入问题的本质,研究高考试题的背景和命题思想.从高等数学的视角研究高考试题,可以更好地理解和认识高考试题背后的知识本源以及命题思想,既可以提升教师试题命制水平,又可以在教学活动中促进学生数学素养的发展.