基于改进傅里叶级数法的任意边界下梁横振特性分析

黄 樱，郭咏梅

基于改进傅里叶级数法的任意边界下梁横振特性分析

黄 樱1，郭咏梅2

（1.河南交通职业技术学院，河南 郑州 450005；2.长安大学，陕西 西安 710000）

【目的】船舶工程、海洋工程、汽车工程等相关领域涉及大量的梁结构，其振动特性直接关系到整体结构的振动控制。【方法】将梁结构横向振动位移采用一种改进傅里叶级数展开，运用Rayleigh-Ritz能量法进行求解，建立任意弹性边界条件下梁横向振动特性统一求解模型；在此基础上，分析不同边界条件对梁结构振动特性的影响规律。【结果与结论】基于改进傅里叶级数，利用Rayleigh-Ritz能量法建立的梁结构振动的求解模型与解析解基本相同，具有良好的准确性，且优于Ansys仿真解。本研究可为船海工程等梁结构振动机理研究与优化提供参考。

欧拉-伯努利梁；横振；任意边界；改进傅里叶法

船舶工程、海洋工程、汽车工程等相关领域涉及大量的梁结构，特别是船舶龙骨、肋骨、纵骨，甲板横梁、纵桁，以及海洋平台主体桁架结构，其振动特性直接关系到整体结构的动力学性能，影响整体结构的正常使用。因此，梁结构振动特性分析对整体结构振动控制具有非常重要的研究意义。目前，国内外学者对梁结构在经典边界条件下的振动解析解进行大量研究，研究方法包括集中质量法、Rayleigh-Ritz能量法、假设模态法、加权参数法（伽辽金法）、传递矩阵法等。鲍四元等[1]基于Rayleigh-Ritz法研究不同截面弹性多跨梁的横向振动。许得水等[2]和周海军等[3]采用改进傅里叶级数法分别研究任意边界下杆扭转振动和轴系回旋振动。周海军等[3-4]推导出带集中质量的梁回旋方程和横向振动方程。杜敬涛等[5]采用改进傅里叶级数研究任意边界下杆纵向振动特性。Hozhabrossadati等[6]采用集中质量法研究Euler-Bernoulli梁的自由振动。Kim等[7]和Li[8-9]均使用傅里叶级数法研究任意边界梁的横向振动。Shin等[10]应用微分变换法分析Euler-Bernoulli梁在变轴力作用下的横向振动。

由于梁结构横向振动求解时会遇到超越方程，计算其固有频率十分困难。因此，有限差分法[11-12]、边界元法[13]和有限元法[14]等数值方法也大量应用于梁结构分析。其中，有限元法是研究该类问题的主要方法，Erdelyi等[15]和钱管良[16]分别使用有限元法研究多层梁和裂纹梁的振动特性。然而，数值方法在求解过程中需要将结构离散化，高频精确度较差，且不适合进行结构参数优化等方面的研究；同时，在实际结构中，振动结构边界条件并非理想的经典边界条件，对弹性边界的研究更具工程价值。鉴于此，本研究提出一种基于改进傅里叶级数法的任意弹性边界条件下梁结构振动特性分析模型，统一傅里叶级数求解方法，分析任意弹性边界下梁的振动特性，以及不同边界条件对梁结构振动特性的影响规律，以期为船舶、海洋平台等骨架的梁结构振动研究提供设计参考。

1 理论建模

1.1 弹性约束边界条件

考虑到梁结构厚度尺寸远小于长度尺寸，本研究使用适用于求解细长结构振动的Euler-Bernoulli梁理论。图1为简化梁结构振动模型，两端引入线性约束弹簧及旋转约束弹簧以模拟弹性边界条件，对应的弹簧刚度分别为0、k、0和K。

当刚度系数取某有限值时，可表示弹性约束边界条件。将弹簧刚度系数取零或无穷大可以模拟自由或固支边界条件（表1）。和分别为梁的长度、杨氏模量、惯性矩和密度，横向振动位移用(,)表示。

图1 弹性边界约束梁横向振动模型

表1 弹簧刚度设定值

根据梁结构两端的力平衡关系，边界条件方程可写为如下形式：

在= 0处，

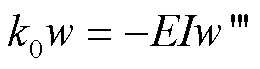
在=处，

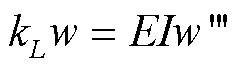
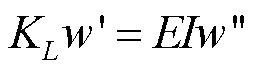
1.2 位移场改进傅里叶级数表达式

在经典边界条件下，振动位移函数可采用傅里叶正弦或余弦级数展开，但是在梁结构两端，即=0或=处，会出现位移导数始终为零的情况，无法研究弹性边界条件下结构的振动。为克服传统傅里叶级数在弹性边界的求导不连续问题，梁结构横向位移采用改进傅里叶级数展开为

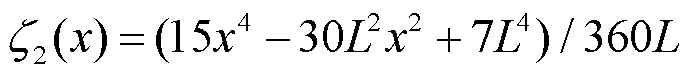
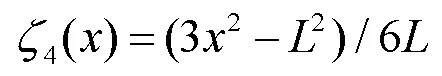
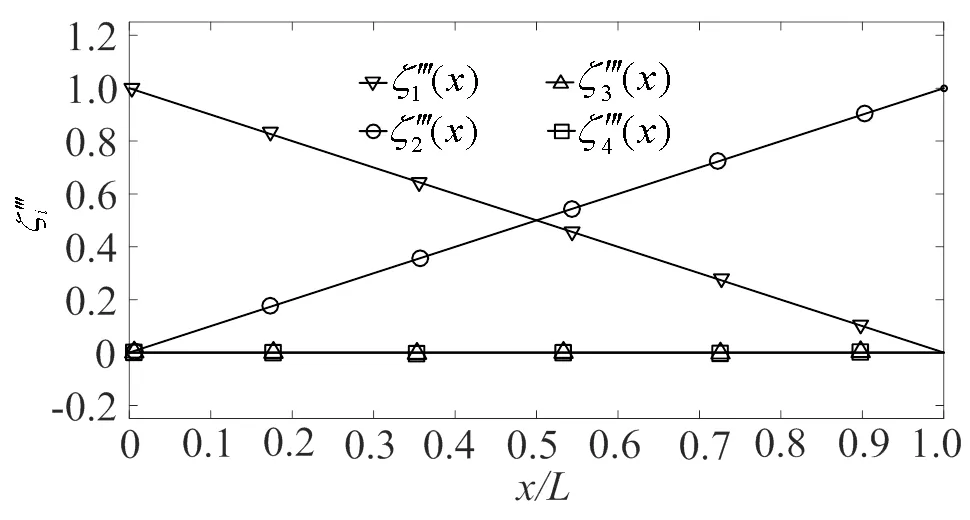
图2 辅助函数及其导数

由图2，可知

1.3 Rayleigh-Ritz法求解

基于改进傅里叶级数，可利用Rayleigh-Ritz能量法结合Hamilton原理来确定振动位移函数的未知系数，从而建立统一的梁结构振动方程求解形式。

无外部作用力时，梁结构的拉格朗日方程为

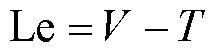
其中，Le是拉格朗日量，是梁结构的总势能，是梁结构的总动能。梁结构的总势能包含两个部分，分别是结构的势能及边界弹簧储存的弹性势能。

任意边界条件下梁（图1）的横向振动总势能表达式为

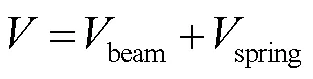
其中，梁结构势能beam为

模拟弹性边界的弹簧势能spring为

梁结构总动能为

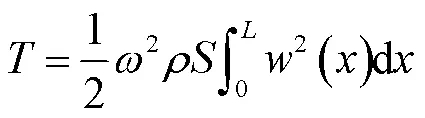
其中，是角频率，是梁的横截面积。

结合Rayleigh-Ritz法及Hamilton原理[17]，对其中每个未知系数求极值，可以得到一系列方程组

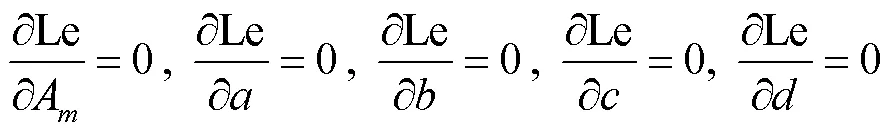
将式(5)带入式(13)，可得矩阵表达形式

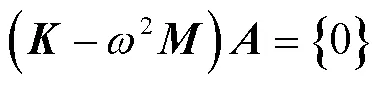
其中，

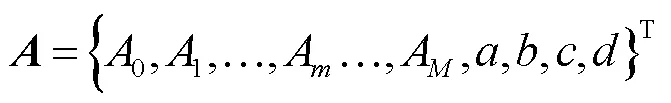
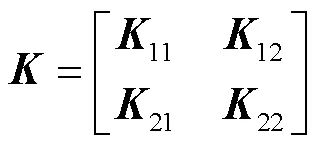
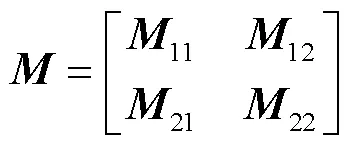
在矩阵、中，11、22和11、22分别为对应傅里叶级数系数和辅助函数系数的对称项，12、21和12、21分别为对应傅里叶级数系数和辅助函数系数的耦合项。

通过以上分析，横向振动的固有频率和特征向量可以通过求解标准特征值问题得到。每一个特征向量包含结构模态的所有未知系数，将系数带入振动位移表达式中即可得到真实的模态。

2 数值算例分析

本研究选取某海洋工程平台梁结构进行仿真模型分析，该平台纵梁为QSTE700TM矩形型材60 mm × 40 mm × 2.5 mm，截面的抗弯惯性矩为2.347 × 10-7m4，横截面积为4.75 × 10-4m2，长度= 3.0 m，材料密度= 7 850 kg/m3，杨氏模量= 2.06 × 1011Pa。为方便后续推导及分析，引入量纲为1系数，线性约束弹簧和旋转约束弹簧刚度系数（量纲为1）分别为

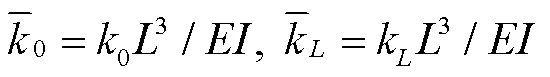
2.1 准确性和收敛性验证

本研究对梁结构自由振动特性进行分析，并与方程解析解、有限元分析计算结果进行对比。本研究使用Ansys软件建立梁结构有限元模型，采用Beam 188单元，Ansys仿真结果与网格精细程度有关。为排除网格尺寸对结果的影响，比较不同网格尺寸下简支梁的Ansys仿真结果（表2），可见当单元数目达到400（单元尺寸0.75 cm）时，Ansys解已经基本收敛，可用于本研究的分析对比。

表2 简支边界条件Ansys解收敛情况

将两端旋转约束弹簧设为0，使线性弹簧刚度逐渐增大，当弹簧刚度足够大时即可模拟简支边界条件。表3列出本研究方法模拟两端线性约束弹簧刚度逐渐增大时前6阶频率的收敛情况（均取相同的傅里叶截断数= 50计算）。由表2可见，当边界约束刚度取值达到1010时，Rayleigh-Ritz能量法结果已经收敛，第1-3阶的频率结果与解析解相同，第4-6阶频率与解析解非常接近，精度高于Ansys解。

表3 模拟简支边界条件线性弹簧刚度系数收敛情况

采用改进傅里叶级数法在计算时需要对傅里叶项数进行截断，为进一步对比不同项数下的收敛速度，表4列出两端简支边界条件下，不同截断数时梁的前6阶固有频率。由表4可见，随着截断数增加，固有频率计算精度逐渐提高，当截断数大于20时，计算结果已基本收敛，可见改进傅里叶级数法的收敛速度非常快。

2.2 不同边界条件对固有频率的影响

从表3中可看出，在弹性边界约束刚度变化时，梁的横向振动变化存在一个较为敏感的取值区间。

图3给出梁从自由-自由边界到简支-简支边界，梁的前6阶固有频率变化趋势。由图3可见，不同阶次固有频率对边界约束刚度变化的敏感程度不同，第1阶固有频率敏感区域在线性弹簧刚度系数（量纲为1）小于102以下，而当刚度系数（量纲为1）取值从103到104时，第4阶到第6阶固有频率变化较快。

表4 改进傅里叶级数截断数收敛情况

图3 固有频率随线性约束弹簧刚度变化

图4给出梁从简支-简支边界到固支-固支边界，梁的前6阶固有频率变化趋势。由图4可见，梁的前6阶固有频率变化敏感区域均在旋转约束弹簧刚度系数（量纲为1）取值100到102之间。

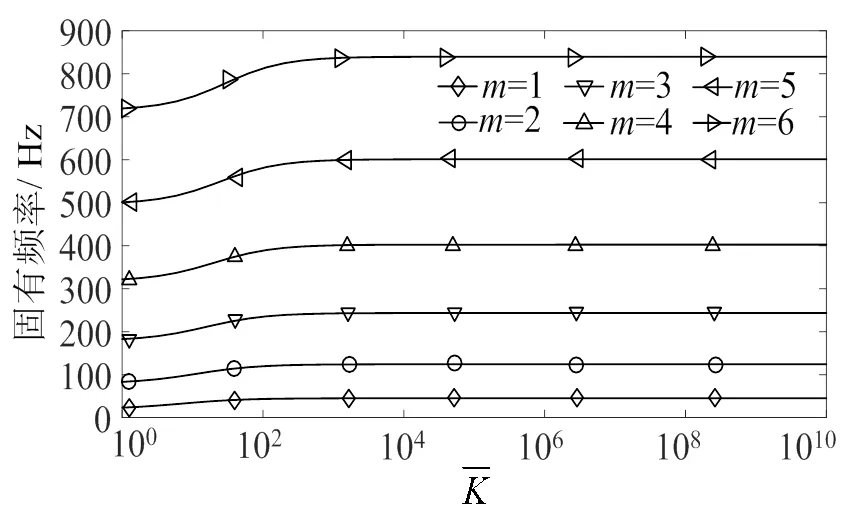
图4 固有频率随旋转约束弹簧刚度变化

图5和图6给出梁结构一端固定（= 0处），一端从自由边界到固支边界（=处），梁结构前2阶固有频率变化趋势。由图5和图6可见，旋转约束弹簧刚度对固有频率的影响要明显大于线性约束弹簧，旋转约束弹簧的影响不能忽视。

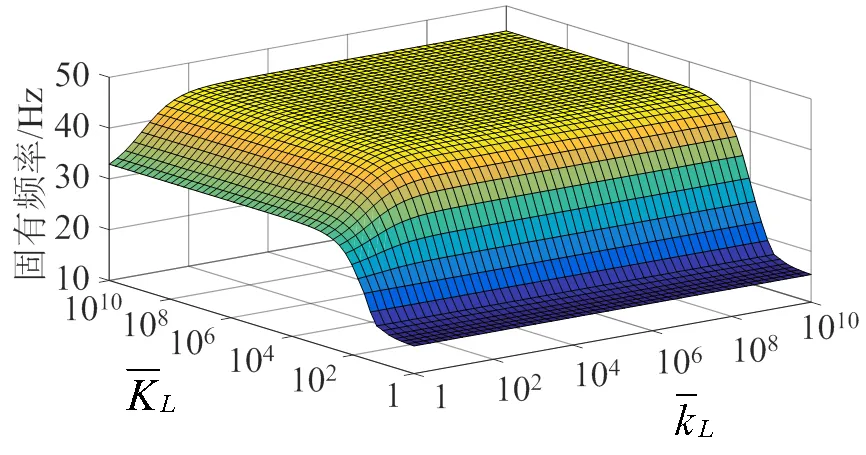
图5 第1阶固有频率随约束弹簧刚度变化

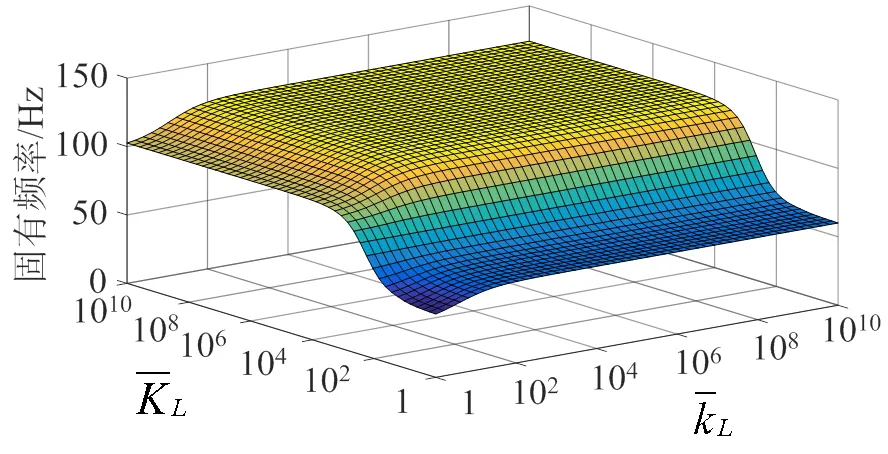
图6 第2阶固有频率随约束弹簧刚度变化

2.3 不同边界条件对模态振型的影响

图7给出梁在自由-自由边界，本研究方法、解析解和Ansys解下的第1阶模态振型。由图7可见，本研究方法和解析解、Ansys解完全一致。

图7 自由状态下梁第1阶模态振型

同样，为分析不同边界约束刚度变化对梁结构模态振型的影响，图8和图9给出梁一端固定，另一端从自由边界到简支边界，梁结构前2阶模态振型的变化趋势。由图8和图9可见，模态振型在线性弹簧刚度（量纲为1）敏感区域会出现剧烈变化，特别是在线性弹簧刚度（量纲为1）敏感区域101到104之间。

图8 变化边界条件第1阶模态振型

图9 变化边界条件第2阶模态振型

3 讨论

将梁结构横向振动位移采用改进傅里叶级数进行展开，带入相应的能量方程，结合Hamilton原理确定位移函数中的未知系数，可快速建立统一的梁结构振动方程求解形式，便于研究任意边界条件下梁结构的振动特性。本方法可以克服传统傅里叶正弦或余弦级数在研究经典边界条件下出现的两端位移导数不连续情况[18]，具有良好的准确性和快速的收敛性。

船舶和海洋平台结构中各类杆件，如船舶结构中的骨架如横梁、肋骨、肋板、纵骨、纵桁等，均可使用本方法进行固有振动特性求解。当然，整个船体结构也可视为船体梁结构[19]，使用本方法快速求得模态信息。对于不规则的梁结构，由于无法给出其具体的能量方程，求解时需要进行一定的简化，使用本方法时会影响其结果的精确性。

船舶结构、海工结构在风浪、海流、地震等冲击力作用下的振动特性分析也具有十分重要的价值[20]，可使用本方法进行下一步研究。对于梁结构在外界激励力作用下的受迫振动求解，只需将外部作用力所做的功引入方程式(8)，进行求解即可。

后续将利用改进傅里叶级数和Rayleigh-Ritz能量法建立的任意边界下梁结构振动求解方法拓展至海洋工程平台板壳理论研究方面。

4 结论

本研究基于Euler-Bernoulli梁理论，利用Rayleigh-Ritz能量法建立梁结构的振动统一求解模型，分析任意弹性边界下梁的振动特性，得到以下结论：

1）利用标准傅里叶级数和辅助函数构建梁结构横向振动位移函数，可消除级数求导过程中边界处的不连续性，具有求解过程统一、收敛速度快的优势。

2）采用两组旋转约束弹簧和线性约束弹簧，可很好地模拟梁结构的任意弹性边界条件，不同阶次固有频率和模态振型变化敏感区域与弹簧刚度有关，前6阶固有频率和振型的刚度（量纲为1）敏感区域均出现在104以下。

3）基于改进傅里叶级数，利用Rayleigh-Ritz能量法建立的梁结构振动的求解模型与解析解基本相同，具有良好的准确性，且优于Ansys仿真解。

[1] 鲍四元, 周静.不同截面形状下弹性支撑多跨梁振动特性分析[J].中国舰船研究, 2020, 15(1): 162-169.

[2] 许得水, 杜敬涛, 李文达, 等.任意边界条件弹性杆结构扭转振动特性分析[J].振动与冲击, 2017, 36(1): 161-166.

[3] 周海军, 吕秉琳, 王东华, 等.一种改进傅里叶级数方法的船舶轴系回旋振动动态特性研究[J].船舶力学, 2012, 16(8): 962-970.

[4] 周海军, 吕秉琳, 杜敬涛, 等.用改进傅里叶级数的方法研究轴系横向振动特性[J].噪声与振动控制, 2011, 31(4): 68-72.

[5] 杜敬涛, 许得水, 吕朋, 等.任意边界条件非局部弹性杆纵振特性分析[J].振动工程学报, 2016, 29(5): 787-794.

[6] HOZHABROSSADATI S M, SANI A A, MOFID M.Vibration of beam with elastically restrained ends and rotational spring-lumped rotary inertia system at mid-span[J].International Journal of Structural Stability and Dynamics, 2015, 15(2): 1450040.

[7] KIM H K, KIM M S.Vibration of beams with generally restrained boundary conditions using Fourier series[J].Journal of Sound and Vibration, 2001, 245(5): 771-784.

[8] LI W L.Free vibrations of beams with general boundary conditions[J].Journal of Sound and Vibration, 2000, 237(4): 709-725.

[9] LI W L.Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions[J].Journal of Sound and Vibration, 2002, 255(1): 185-194.

[10] SHIN Y J, YUN J H.Transverse vibration of a uniform Euler-Bernoulli beam under varying axial force using differential transformation method[J].Journal of Mechanical Science and Technology, 2006, 20(2): 191-196.

[11] 许士菊, 王长华.梁振动方程的一个稳定的有限差分近似[J].吉林化工学院学报, 2007, 24(1): 79-81.

[12] 姚振汉, 王海涛.边界元法[M].北京: 高等教育出版社, 2010: 25-78.

[13] 韩旭炤, 黄玉美, 张永贵, 等.梁结构振动问题的边界元法解析[J].农业机械学报, 2008, 39(7): 178-182.

[14] Mackerle J.Finite Element Vibration Analysis of Beams, Plates and Shells[J].Shock and Vibration, 1998, 6(2): 97-109.

[15] ERDELYI N H, HASHEMI S M.On the Finite Element Free Vibration Analysis of Delaminated Layered Beams: A New Assembly Technique[J].Shock and Vibration, 2016(4): 1-14.

[16] 钱管良.计算含裂纹圆截面梁振动的有限元法[J].机械强度, 1992, 14(1): 7-10.

[17] SOEDEL W.Vibrations of Shells and Plates(Third edition) [M].New York: Marcel Dekker Inc., 2004.

[18] ZHENG D Y, DU J T, LIU Y.Vibration characteristics analysis of an elastically restrained cylindrical shell with arbitrary thickness variation[J].Thin-Walled Structures, 2021, 165: 107930.

[19] 桑国光, 龚恢.船体梁抗弯能力的计算[J].中国造船, 1984, 25(1): 65-74.

[20] ISLAM M S, KHALIL G M.Dynamic analysis of a fixed ended beam with focus on vibration neutralization in ship hull structure[J].International Journal of Engineering Research and Technology, 2014, 3(1): 2050-2064.

Transverse Vibration Characteristics Analysis of Beam with General Boundary Conditions Based on Improved Fourier Series Method

HUANG Ying1, GUO Yong-mei2

（1.,450005,; 2.’,’710000,）

【Objective】Beam structure is widely used in various engineering occasions, such as ship engineering, ocean engineering, automobile engineering etc., and its vibration characteristics have a directs influence on the vibration control of the whole structure.【Method】The transverse vibration displacement of the beam structure is expanded by a modified Fourier series and solved by the Rayleigh-Ritz energy method to establish a unified solution model for the transverse vibration characteristics of the beam under general elastic boundary conditions.With the model developed, the influence of different boundary conditions on the vibration characteristics of beam system is studied and discussed.【Result and Conclusion】Based on the improved Fourier series, the beam vibration model established by Rayleigh-Ritz energy method is basically the same as the analytical solution, with good accuracy and surpasses the Ansys simulation solution.The study provides a very important reference for the research and vibration optimization of beam structures in ship and ocean engineering.

Euler-Bernoulli beam; transverse vibration; general boundaries; improved Fourier series method

U662.2

A

1673-9159（2022）02-0135-07

10.3969/j.issn.1673-9159.2022.02.017

2021-07-28

2019年度河南省高等职业学校青年骨干教师培养计划项目（2019GZGG102）

黄樱（1982―），女，硕士，副教授，研究方向为交通运输规划与管理。E-mail: topworker0@protonmail.com

黄樱，郭咏梅.基于改进傅里叶级数法的任意边界下梁横振特性分析[J].广东海洋大学学报，2022，42（2）：135-141.