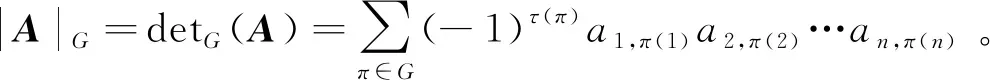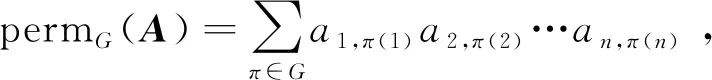公理化定义矩阵行列式的性质推导
赵姣珍,许道云
(1.贵阳人文科技学院 大数据与信息工程学院,贵州 贵阳 550025;2.贵州大学 计算机科学与技术学院,贵州 贵阳 550025)
矩阵的行列式值是矩阵的一个不变量,它是代数中一个重要的基础概念,对矩阵各种性质研究以及矩阵在其他领域中的应用,几乎都与行列式相关。本文考虑的矩阵均指n阶方阵,给定一个n阶矩阵,可用列向量表示为
通常,矩阵的行列式定义以如下公式给出[1]:
(1)
其中,π是集合{1,2,…,n}上的一个置换。置换π可以被分解为对换的乘积,π的奇偶性由它被分解为最少对换个数的奇偶性决定,此与序列(π(1),π(2),…,π(n))的逆序数(记为τ(π))的奇偶性一致。式(1)中的求和则是取遍{1,2,…,n}上的所有置换。
从式(1)可以找到二阶和三阶行列式的计算规律,并用于计算。但对于四阶以上的n阶行列式,利用式(1)作为计算公式是不现实的。实际计算时,主要是基于行列式的性质不断地降阶,或化为特殊矩阵,或按性质进行计算。
一般,有关行列式的性质是由式(1)推导,部分性质推导较为复杂。基于公理化定义的行列式,从公理形式出发进行推导,在逻辑思路、推导过程、简洁性等方面都有其优点。
文献[2]中以矩阵的列向量(A1,A2,…,An)作为变量,引入行列式函数,以公理形式给出了行列式定义。
本文基于公理本身,讨论了公理的等价性和独立性,从公理化定义行列式出发,直接导出行列式常见的基本性质和普通定义计算式(1),并给出相关重要性质的推导。
1 行列式的公理化定义及等价公理
定义[2]设矩阵A=(A1,A2,…,An),考虑一个实数函数det(A1,A2,…,An),如果函数满足如下公理条件,则称det(A1,A2,…,An)为矩阵A的行列式。
公理1对于任意固定的(1≤k≤n),以Ak为变量,其余列不变的情况下诱导出的函数detk(Ak)具有齐次线性性质。即,对于任意常数a,b,detk(aAk+bBk)=adetk(Ak)+bdetk(Bk)。
公理2若存在相邻两列相等,其值为0。即,如果存在某个1≤k 公理3对于单位矩阵U=(U1,U2,…,Un),det(U1,U2,…,Un)=1。其中Uk为第k个单位向量。 首先,可由公理条件直接推出如下基本性质: 性质1如果矩阵中有一列全为0,则行列式为0。 事实上,如果矩阵A的第k列全为0,由公理1中的齐次性,有detk(0)=detk(0·0)=0·detk(0)=0。 性质2将矩阵中一列的c倍加到相邻一列后,则行列式不变。 假设由矩阵中的第k+1列的c倍加到第k列,则新矩阵的第k列为Ak+cAk+1。由公理2,detk(Ak+1)=0。再由公理1,有detk(Ak+cAk+1)=detk(Ak)+c·detk(Ak+1)=detk(Ak)。 性质3将矩阵中相邻两列互换后,行列式改变符号。 证明设A=(A1,…,Ak,Ak+1,…,An),两列互换后得到矩阵A′=(A1,…,Ak+1,Ak,…,An)。 将矩阵A中第k列加到第k+1列,得到B=(A1,…,Ak,Ak+Ak+1,…,An);将矩阵B中第k+1列的(-1)倍加到第k列,得到C=(A1,…,(-1)Ak+1,Ak+Ak+1,…,An);将矩阵C中第k列加到第k+1列,得到D=(A1,…,(-1)Ak+1,Ak,…,An)。 由性质2以及公理1中的齐次性质,有 det(A1,…,Ak,Ak+1,…,An) =det(A1,…,Ak,Ak+Ak+1,…,An) =det(A1,…,(-1)Ak+1,Ak+Ak+1,…,An) =det(A1,…,(-1)Ak+1,Ak,…,An) =(-1)·det(A1,A2,…,Ak+1,Ak,…,An) 性质1~3完全由公理本身得到。很显然:①性质1和性质2可以导出公理2;②性质1和性质3也可以导出公理2。换言之,分别以性质1和性质2取代公理2,以性质1和性质3取代公理2,可以得到行列式函数的另外两个等价公理定义。 请注意:公理定义中公理1和公理3是本质的。 下面的性质表明:公理2、性质2和性质3中的“相邻”条件可以去掉。 性质4将矩阵中不同两列互换后,行列式改变符号。 证明指定两个不同列号i,j(i 因此,一共作了奇数次相邻列互换。由性质3,det(A)=(-1)det(C)。即:矩阵中不同两列互换后,则行列式改变符号。 类似证明: 性质5如果矩阵中有两列相等,则行列式为0。 性质6将矩阵中任一列的c倍加到另一列后,行列式不变。 证明任意指定两个不同列号i,j(i 由性质4,det(A)=(-1)det(B); 由性质2,det(B)=det(C)。再由性质4,det(C)=(-1)·det(D)。所以,det(A)=det(D)。即:矩阵中任一列的c倍加到另一列后,行列式不变。 (4,6,5,7)(9),其轮换的长度分别为:3,1,4,1。通常,略去单点轮换后简单地表示为π=(1,2,8)(4,6,5,7),未出现的元素表示自己映射到自己。长度为2的轮换称为对换。 可以验证:一个长度为k的轮换可以表示成k-1个对换的复合,且为最小对换个数: (2) 假定将一个置换π分解为轮换积形式时,其轮换的长度序列为l1,l2,…,lm,则一个置换π可以表示为(l1-1)+(l2-1)+…+(lm-1)个对换的复合。记 τ#(π)=(l1-1)+(l2-1)+…+(lm-1) 它记录了置换π表示为对换的个数。 可以证明: 1)τ#(π)是置换π表示为对换时的最小对换个数。因此,这个数是唯一的,以其奇偶性定义置换π的奇偶性。 2)τ#(π)的奇偶性与整数序列(π(1),π(2),…,π(n))的逆序数τ(π)的奇偶性一致。 事实上,单位置换对应的逆序数为0。相邻元素作对换后,逆序数的改变相差1。一般对换使用后,逆序数的改变相差一个奇数。 有了上面的讨论,由性质4,我们有: 性质7给定A=(A1,A2,…,An),以及列号集{1,2,…,n}上的一个置换π,有如下关系: det(Aπ(1),Aπ(2),…,Aπ(n))=(-1)τ(π)det(A) (3) 特别,由公理3,对于单位矩阵U=(U1,U2,…,Un),我们有 det(Uπ(1),Uπ(2),…,Uπ(n))=(-1)τ(π) (4) 其中,τ(π)为整数序列(π(1),π(2),…,π(n))的逆序数。 矩阵行列式有一条重要性质:矩阵A的行列式与其转置AT的行列式相等。我们现在来看一下这条性质如何从公理出发得到。 首先,我们注意到:对于单位矩阵U,U=UT。从而,det(UT)=det(U)=1。 (5) 将公理1应用到式(5)中,从第1个列向量开始,依次展开: (6) 由性质5,矩阵中有两列相等时,行列式为0。因此,式(6)完全展开后得到 其中,求和是取遍{1,2,…,n}上所有置换。 为了看清楚这一点,读者可以n=3推导式(7)。 由式(4),我们有 (8) 同样,对于 A=(A1,A2,…,An) 行列式展开后得到 我们知道:{1,2,…,n}的所有置换π,在复合运算下构成对称群Sn,对于任一个置换π,逆元π-1与π一一对应,并且τ#(π-1)=τ#(π)。从而,(-1)τ(π-1)=(-1)τ#(π-1)=(-1)τ#(π)=(-1)τ(π)。 改写式(9)中系数项中的乘积顺序。行、列下标自然顺序调整有如下关系: aπ(1),1aπ(2),2…aπ(n),ndet(Uπ(1),Uπ(2),…,Uπ(n)) =a1,π-1(1)a2,π-1(2)…an,π-1(n)det(Uπ-1(1),Uπ-1(2),…, Uπ-1(n)) (10) 因为 aπ(1),1aπ(2),2…aπ(n),ndet(Uπ(1),Uπ(2),…,Uπ(n)) =(-1)τ(π)a1,π-1(1)a2,π-1(2)…an,π-1(n)det(U1,U2,…,Un) =(-1)τ(π)+τ(π-1)a1,π-1(1)a2,π-1(2)…an,π-1(n)· det(Uπ-1(1),Uπ-1(2),…,Uπ-1(n)) =a1,π-1(1)a2,π-1(2)…an,π-1(n)det(Uπ-1(1),Uπ-1(2),…,Uπ-1(n)) 因此,我们有 det(Uπ(1),Uπ(2),…,Uπ(n)) det(Uπ-1(1),Uπ-1(2),…,Uπ-1(n)) (11) 当求和取遍所有置换时,有如下关系: Uπ-1(2),…,Uπ-1(n)) Uπ(2),…,Uπ(n)) Uπ(2),…,Uπ(n)) =det(AT) (12) 由此,有如下性质: 性质8矩阵A的行列式与其转置AT的行列式相等。即,det(AT)=det(A)。 有了性质8,行列式公理定义中,由“列向量”改为“行向量”作变量定义行列式函数同样有上述平行性质。因此,有关“列”的性质,对“行”同样成立。 同时,由式(11)及公理3,我们可以得到通常行列式的定义公式: det(Uπ(1),Uπ(2),…,Uπ(n)) det(U1,U2,…,Un) (13) 其中,求和是取遍{1,2,…,n}的所有置换π,一共有n!项。 由于是对全体置换求和,我们有 (14) 在上述推导过程中,我们得到如下2个有用公式: (15) (16) 注意:式(15)中,等式左端矩阵部分是取A的转置AT,右端求和系数项中的乘积是以行标为自然顺序;而在式(16)中,等式左端矩阵部分是取A,右端求和系数项中的乘积是以列标为自然顺序。 用公理方法,可以自然地推出著名的Laplace定理:矩阵乘积(矩阵乘)的行列式等于矩阵行列式的乘积(实数乘)。即,det(AB)=det(A)det(B)。 设有两个同阶方阵A和B,其矩阵乘法AB形式可以表示为 (17) 仿式(15)(16),我们有 det(Aπ(1),Aπ(2),…,Aπ(n)) det(Aπ-1(1),Aπ-1(2),…,Aπ-1(n)) det(A1,A2,…,An) =det(A1,A2,…,An)· =det(A1,A2,…,An)· =det(A1,A2,…,An)·det(B1,B2,…,Bn) =det(A)·det(B) 其中 是依据求和取遍{1,2,…,n}的所有置换。 我们知道:高阶行列式的计算主要是通过降阶。 由公理得到的一些主要性质(如:行(列)互换行列式变号,一行(列)的c倍加到另行(列)行列式不变),以及如下的降阶原理可以计算n阶行列式。 对于n阶矩阵A=(A1,…,An),可以表示成如下形式: (18) 如果A中第1行全为0,则det(A)=0,否则至少有一个不为0。于是,通过适当的列互换,以及第1(行)列的某个倍数加到另一(行)列,矩阵可化为如下形式: (19) 其中,矩阵B=(B2,…,Bn)为n-1阶方阵。对于形如式(19)的矩阵,利用已经由公理推导出的行列式 可以推导出:det(A)=adet(B)。 我们现在观察n阶矩阵A的行列式分解为它的n-1阶子矩阵的行列式之间的关系: 对于式(18)表示的矩阵A,记A[i,j]为在矩阵A中删去第i行、第j列后得到的n-1阶子矩阵。 展开如下公式: =a1,1det(A[1,1])+ =a1,1det(A[1,1])+… 我们有 (20) 一般地,对于固定的i,有如下分解计算公式: (21) 对于式(20),对于2≤i≤n,由两行相同行列式为0,我们有 (22) 由此导出一条重要性质:如果行列式det(A)≠0,对于第1个n维单位向量U1,线性方程组 x1A1+…+xnAn=U1 有解,其中解x(1)的分量 (23) 一般地,类似方法可得到:如果行列式det(A)≠0,对于第k个n维单位向量Uk,线性方程组 x1A1+…+xnAn=Uk 有解,其中解x(k)的分量计算公式为 (24) 请注意:在det(A)≠0条件下,文中线性方程组解的存在性完全由公理及行列式性质独立推出,并非由det(A)≠0条件按如下路径得到:A1,…,An线性无关,由A1,…,An构成Rn空间的生成系,再由生成系生成B(如文献[2])。由生成系生成B要用到线性方程组的解,从逻辑上讲,这里出现一个循环推导问题。 将式(23)(24)组合在一个公式中,得到 由此,矩阵A的逆矩阵 ci,j=(-1)i+jdet(A[i,j]) (25) 这就是可逆矩阵的逆矩阵计算公式(方法)——代数余子式方法。 行列式之所以重要,最主要的原因之一是它提供了求解线性方程组的一般方法:克莱姆(Cramer)法则。 公理化定义的行列式很容易导出克莱姆法则,这体现了公理化方法的优点。 给定一组n维列向量A1,…,Am,称A1,…,Am线性相关,指:存在其中一个列向量Ak,Ak可以表示由其余列向量的线性组合表示。如果不是线性相关,则称为线性无关(或线性独立)。 线性相关等价于:存在一组不全为0的数α1,…,αm,使得α1A1+…+αmAm=0。线性无关等价于:对任意一组数α1,…,αm,如果α1A1+…+αmAm=0,则α1=…=αm=0。 在讨论线性方程组解的存在性与系数矩阵的行列式之间的关系之前,从逻辑上讲,我们应该先考虑行列式与列向量线性相关性质之间的关系,而不是从线性方程组解的性质讨论这一关系。 关于向量组的线性相关性质,容易验证:①在一个向量组中,如果存在部分向量构成的子向量组线性相关,则该向量线性相关;②对一组n维列向量A1,…,Am,B1,…,Bm是由A1,…,Am在同一位置(如第1位置)插入0后得到n+1维向量组,则A1,…,Am与B1,…,Bm的线性相关性一致。 由第3节得到的性质,我们可以得到如下性质: 性质9对于矩阵A=(A1,…,An),如果det(A1,…,An)=0,并且A第1列都不全为0,则通过如下操作: 1)调整行的顺序使(1,1)位置元素不为0; 2)将第1列的某个倍数加到第2,…,n列某一列,得到矩阵 其中det(B2,…,Bn)=0。 请注意:第一类操作只可能改变行列式符号,第二类操作不改变行列式值,因此 性质9就是通常将一个矩阵划为三角矩阵的方法:行列式值只改变符号。对于行列式为0的原始矩阵,每一步操作后所得到矩阵的行列式仍为0,并且A1,…,An与B1,…,Bn的线性相关性一致。 请注意:对于一阶矩阵,当其行列式为0时,该矩阵只能为零矩阵。 由上述讨论,矩阵A=(A1,…,An)中,A1,…,An的线性相关性可以由A的行列式值是否为0判定。 性质10对于矩阵A=(A1,…,An),向量组A1,…,An的线性相关性当且仅当det(A)=0。 证明如果A1,…,An线性相关,则存在一个列向量Ak,Ak=α1A1+…+αk-1Ak-1+αk+1Ak+1…+αnAn,则由性质6及性质1,det(A1,…,Ak,…,An)=det(A1,…,0,…,An)=0。 反之,如果det(A)=0,如果A中有一列向量全为0,则A1,…,An中含有零向量,从而线性相关。否则,取定A1,其中至少有一个非零分量。按性质9,从A可以得到一个形式如下的矩阵: 其中det(B)=det(B2,…,Bn)=0,且A1,…,An与B1,…,Bn的线性相关性一致。 对B重复上述操作(至多n-1次),可以在某一步上得到C=(Ck,…,Cn)(1 利用性质10,我们得到如下行列式与线性方程解之间的关系。 性质11对于线性方程x1A1+…+xnAn=B,我们有: 1)如果对于任意一个n维列向量B,方程有解,则det(A1,…,An)≠0。 2)如果det(A1,…,An)≠0,则对于任意给定的一个n维列向量B,方程有解。从而,如果存在某个n维列向量B,方程无解,则det(A1,…,An)=0。 证明1) 假定对于任意的n维列向量B,方程有解,分别取B为单位向量U1,…,Un,记方程x1A1+…+xnAn=Ui的解为Bi,则(A1,…,An)(B1,…,Bn)=(U1,…,Un)。因此 det((A1,…,An)(B1,…,Bn)) =det(U1,…,Un)=1 由Laplace定理: det((A1,…,An)(B1,…,Bn)) =det(A1,…,An)det(B1,…,Bn) 从而,det(A1,…,An)≠0。 而解x*的分量由如下公式计算: 可以验证 =det(A1,…,Ak-1,B,Ak+1,…,An) 从而 这就是Cramer法则对解向量的分量的计算公式。 反过来,如果det(A1,…,An)≠0,且方程x1A1+…+xnAn=B有解(请注意,这里先假设有解),则解向量中分量xj可以表示为 这就是著名的Cramer法则。 Cramer法则的推导:由x1A1+…+xnAn=B,以第1列为例:将B替换A1,计算行列式det(B,A2,…,An)。由性质6,从第2列至第n列,分别以第k列的-xk倍加到第1列(行列式不变),最后使用公理1得 det(B,A2,…,An) =det(x1A1+x2A2+…+xnAn,A2,…,An) =det(x1A1+x3A3+…+xnAn,A2,…,An) … =det(x1A1,A2,…,An) =x1det(A1,A2,…,An) 在行列式的公理定义中,三条公理是相互独立的。原因是:公理1只考虑矩阵中任一列上的齐次线性性质;公理2是考虑矩阵中两列比较,不涉及运算;公理3是界定行列式函数的“初始”边界值,以单位矩阵U的行列式为1作为“种子值”。因此,由其中任意两个公理不能导出第三条公理。 其次,根据第1节中的讨论,行列式的公理定义中的公理2有两种替换方式。 对于公理3,可修改det(U1,U2,…,Un)的初始值。如:定义一个函数F(A)=F(A1,…,An)满足公理1和公理2,修改公理3为F(U)=F(U1,…,Un)=c≠0,则可以证明:F(A1,…,An)=c·det(A1,…,An)。 更进一步,我们可以将F(A)=F(A1,…,An)的取值不是定义在实数集上,而是定义于一个域上(或者一个抽象空间上),通过适当规定公理,可以将矩阵的性质映射到相应空间上。同样,可以修改公理,研究满足公理的函数的相关性质。 有关行列式的定义方式,还可以用Valiant给出的图论方法引入,相关定义请参见文献[3-4]。对于高阶稀疏矩阵行列式的计算,有时以图的方式引入的定义更有效。对于MacMahon主定理、Cayley-Hamilton定理、矩阵树定理、特征多项式定理等的证明,图论方法引入行列式体现了新的思路。详细介绍请参阅文献[5-10]。 a1,π(1)a2,π(2)…an,π(n),其求和是对集合J={1,2,…,n}上所有置换求和,即在对称群Sn中取每个元素作用于列标号集J。我们知道:对于定义在J上的任意一个(有限)群G,都对应产生Sn的一个子群。或者说,G同构于Sn的一个子群。2 行列式的其他性质
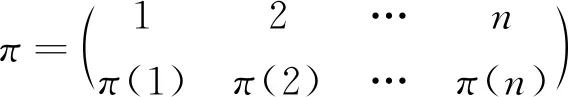
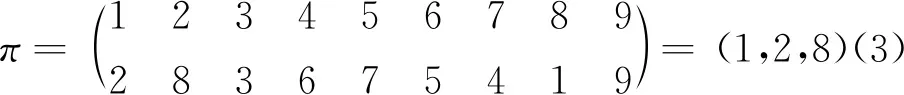



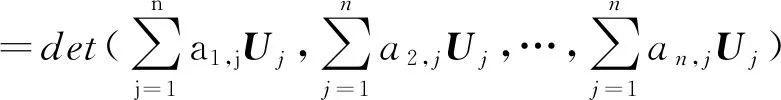


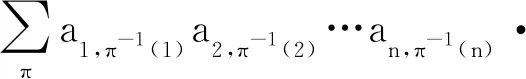
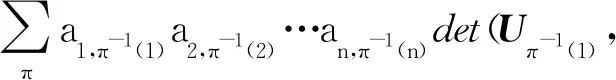
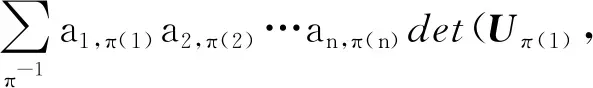
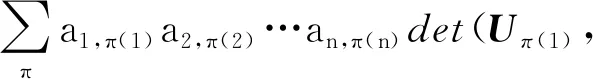
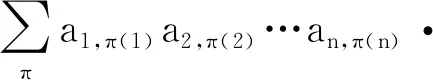
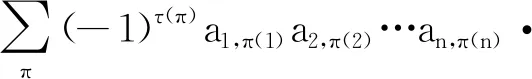
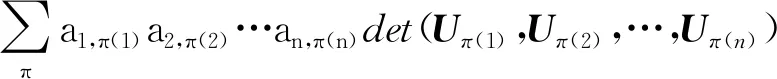
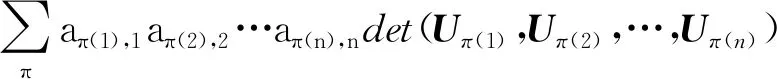
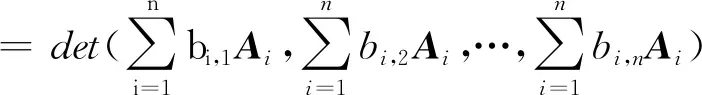
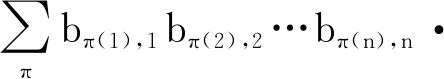
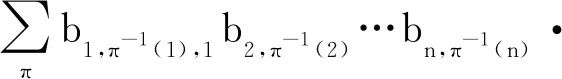
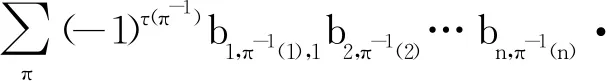
3 高阶行列式降阶与行列式的分解
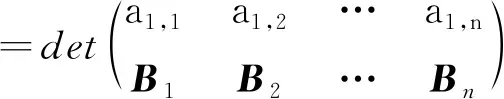
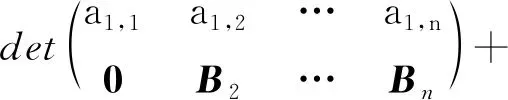
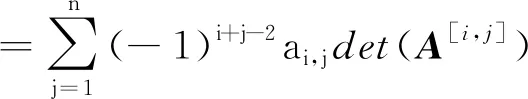
4 线性方程组解的存在性及解的表示
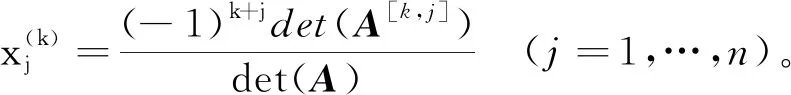

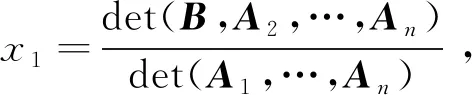
5 结语