基于径向基神经网络的船舶运动智能预报

樊翔，程陈，侯先瑞，施文煜，桂皓

（1.上海船舶研究设计院，上海 201203；2.上海海事大学，上海 201303）

0 前 言

由于海况的复杂性， 船舶在航行过程中会受到风、浪、流等因素的综合作用而产生垂荡、横摇、纵摇等摇荡运动， 严重时将威胁船舶航行和作业安全。 若能提前对船舶运动姿态进行预报，进而对船舶的相关操作做出预判， 便可使船舶航行时有效规避风险，进而提高船舶航行的安全性［1］。因此，如何有效地对船舶运动进行实时准确预报， 一直是船舶与海洋工程领域重点关注的热点问题之一。

为准确预报船舶运动，国内外学者［2-4］相继提出了多种预报方法，根据这些方法的理论基础。 从理论范畴来看，可分为基于线性系统理论的方法（卡尔曼滤波法、时间序列的回归预报模型等）［5-6］，基于非线性系统理论的方法 （基于突变理论的预报方法、基于混沌理论的预报方法、小波分析的预报方法等）［7-9］，以及基于机器学习理论的预报方法（人工神经网络、支持向量机、深度学习算法等）［10］。 从船舶运动特性来看，又可以分为平稳线性预报、平稳非线性预报、 非平稳线性预报和非平稳非线性预报。 船舶运动预报方法分类如图1 所示。

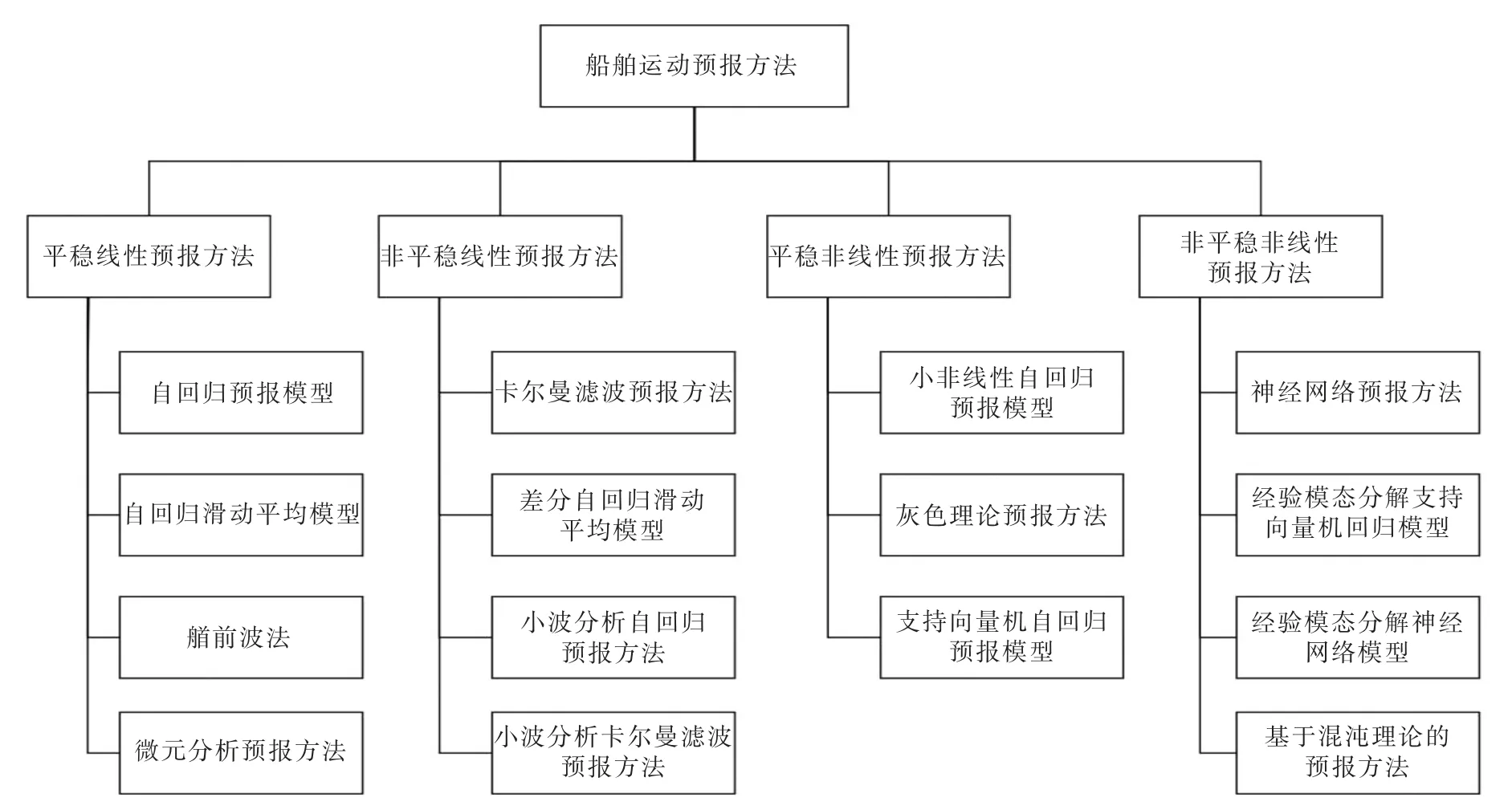
图1 船舶运动预报方法

近十年来，随着人工智能技术的发展，尤其是随着深度神经网络技术的进步，利用神经网络对船舶运动进行预报逐渐受到众多研究者的关注。 鉴于船舶运动的非线性特性，将人工神经网络用于船舶运动预报领域，可以借助人工神经网络的自适应自学习及无限逼近非线性函数的能力，通过对大量历史数据的学习来模拟船舶在各种情况下的运动规律。 在国内外学者的共同努力下，已有多种神经网络模型用于船舶运动预报领域并取得了不错的成果。 基于人工神经网络理论，通过构造基于径向基函数（Radial Basis Function，RBF）的神经网络模型，分别对船舶在波浪中的横摇、 垂荡-纵摇运动进行预报研究，以期实现对其的准确预报。

1 人工神经网络简介

人工神经网络是对人体神经系统的概念化想象的仿生模型，其原理是模拟生物神经元的学习过程。 为了仿效生物的神经结构，神经元是神经网络的基础处理单元。 神经元包括输入、输出和数据处理等3 个部分。 神经元的输入接受的上一层所有神经元的输出， 而不和本层的其他神经元进行关联。神经网络的基本结构如图2 所示。

图2 神经网络的基本结构

单层神经元模型（感知器模型）包括输入层和输出层，两层之间使用权值连接。 所谓训练就是通过算法来更新权值使得网络的误差不断减少，预报效果达到最佳。例如，输入变量为［a1，a2，a3］T，用向量a表示，输出为z，权重为w，偏置为b，则神经元的输出表示为z=g（wa+b）。 其中，函数g 表示神经元的激活函数，其作用是对线性叠加后的数据进行非线性映射。 在神经网络中经常使用的激活函数包括双曲正切激活函数、Sigmoid 型激活函数、 线性整流激活函数等。 单层神经网络仅能处理一些简单的问题，对复杂的问题如异或问题无能为力，需要应用多层神经网络模型。 与感知器模型相比，多层神经网络多了一个中间层，即隐含层（隐含层可以有多层），可以实现对任意非线性函数的高精度逼近。

在对多层神经网络模型进行训练学习时，需要根据学习误差调整神经网络各层的权值和偏置，其中经典的学习算法就是误差反向传播（Back Propagation，BP）算法。 BP 算法的基本原理：首先，利用当前各层的权重和偏置值，计算每一层对输入样本的输出值；其次，计算各输出层节点的误差，并根据链式求导法则计算损失函数对权重和偏置的梯度值； 最后，采用梯度下降法更新各层神经元的权重和偏置。

RBF 神经网络特点就是它的隐含层函数为RBF。RBF 函数是中心点径向对称，取值仅依赖于距中心点距离的非负实值函数。 通常情况下，隐含层有较高的维数， 这就使得它能够更加精确地逼近。常见的基函数有多二次函数、薄板样条函数、逆多二次函数和高斯函数等，其中高斯RBF 函数的表达式如式（1）所示：

式中：参数σ 描述高斯基函数的宽度或“平坦程度，其值越大意味着以c 为中心的等高线越稀疏。

与传统的BP 神经网络不同，RBF 神经网络是一个局部逼近的网络， 即各节点对输出的贡献取决于其距离中心的欧氏距离，距离越大的贡献越小。 这种局部逼近使得它的收敛速度更快，学习效果更好。

2 基于径向基（RBF）神经网络的船舶运动预报

图3 是应用RBF 神经网络模型对船舶的运动姿态进行预报的算法流程图。

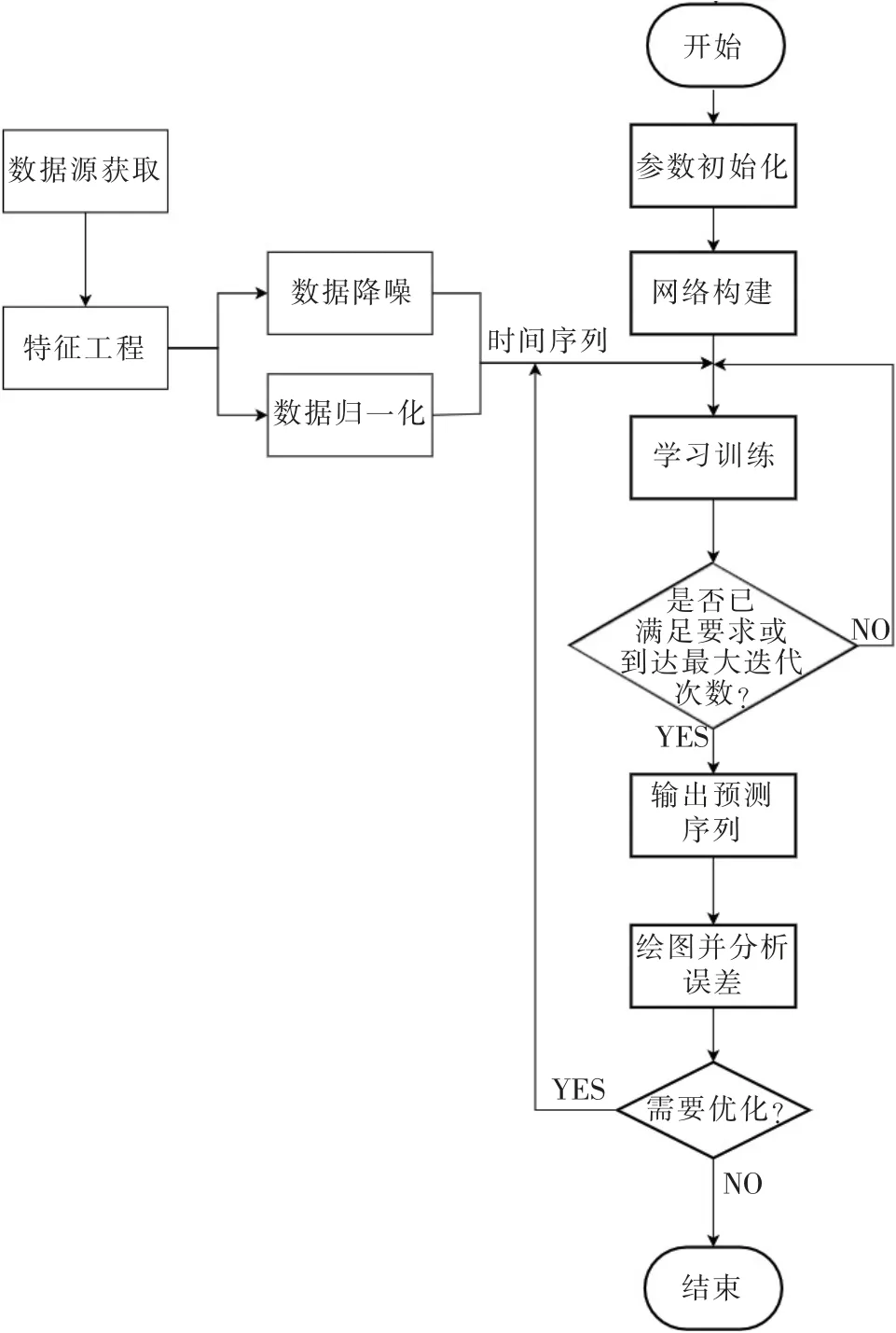
图3 RBF 神经网络船舶运动预报流程图

2.1 数据预处理

主要包括数据的收集、 数据降噪和归一化处理。 采用的数据来自某FPSO 船的试验数据。 该FPSO的垂线间长为356.00 m，型宽为69.00 m，型深为35.70 m，吃水15.2 m。通过试验得到该船的横摇、垂荡-纵摇运动数据后， 受到测量设备本身或是传输中的各种因素影响，原始数据可能是冗余、含有噪声的，因此需要对其进行预处理。 具体采用小波变换法对原始数据进行降噪，并对降噪后的数据进行归一化和标准化处理。采用Min-Max 归一化处理方法，见式（2）。

为提高收敛效率，对数据进行正则化处理：

式中：μ 为样本数据均值；σ 为样本数据的标准差。

2.2 构建RBF 神经网络模型

RBF 神经网络模型的确定是关键环节，模型结构是否合理直接影响到最终的预报结果的准确性。基于处理好的数据， 通常将数据划分为训练集、交叉验证集和测试集等3 部分，通过对交叉验证集的损失函数评估来确定模型的雏形，通过对训练集的损失函数评估来确定参数，而测试集用来检测网络模型的泛化能力。 RBF 神经网络在进行预报时，除需要确定网络的输入层、隐含层、输出层节点个数外，还需确定径向基函数的中心和宽度等。 RBF 网络有多种方法可以确定中心，最常用的有随机选择法、k-means 聚类算法、自组织选取中心法和正交最小二乘法等。采用k-means 聚类算法确定RBF 神经网络的中心。

3 结果分析

3.1 船舶横摇运动智能预报

基于上述FPSO 船在有义波高15.0 m、 风速39.0 m/s、谱峰周期15.1 s、表层流速2.0 m/s 下的横摇运动模型试验数据，利用300 组样本，划分训练集、交叉验证集和测试集，通过多次训练之后确定隐层节点数为300。

取径向基扩展系数为0.3、迭代次数为300 时，误差评价函数为均方误差， 训练曲线如图4 所示，可以看到，在大约250 次迭代之后，网络达到收敛。

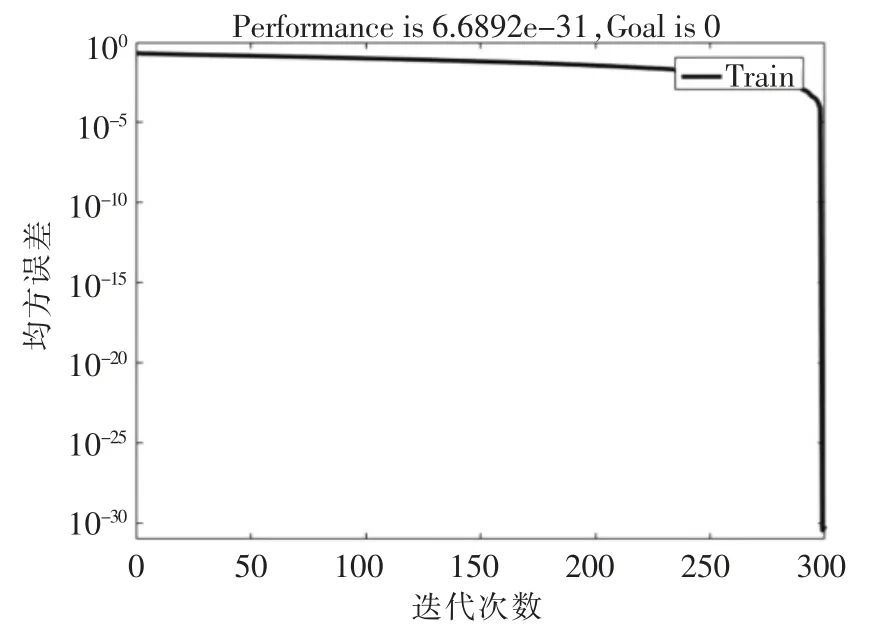
图4 RBF 神经网络横摇运动均方误差训练曲线

利用训练后的网络， 分别取输入层数据为10 s（20 节点）、15 s（30 节点）和20 s（40 节点）横摇角序列， 预报后7 s 的横摇角序列， 预报结果如图5 所示：实线为实测的船模试验数据，称为期望值，虚线为预报结果，称为预报值。

图5 RBF 神经网络横摇运动预报结果

分析结果可知，取前15 s 的历史数据作为输入时，可以得到更好的预报结果，预报曲线拟合得更好。 但使用20 s 的历史数据时，预报精度没有明显提升，与15 s 预报结果相差不大。 为验证RBF 神经网络模型的有效性， 特别构建BP 神经网络进行对比， 对输入层为15 s 的横摇角时间序列进行预报，其结果如图6 所示。

图6 BP 神经网络横摇运动预报结果

通过对比可知，BP 神经网络的训练过程长达10 min 以上，而使用RBF 神经网络只需要5～8 s 就可以完成训练，结果证明RBF 神经网络具有更快的收敛速度， 同时从预报拟合曲线也可以看出，RBF神经网络具有更高的预报精度。

3.2 船舶垂荡-纵摇运动智能预报

与横摇类似， 使用构建好的RBF 神经网络模型，分别取历史数据为10 s 和15 s 的时间数据对船舶的垂荡-纵摇时间序列进行预报， 结果如图7 所示。

图7 RBF 神经网络垂荡-纵摇耦合运动预报

由以上结果可以得到，径向基神经网络可以通过快速训练实现对船舶运动姿态长达7 s 的预报，且对目标曲线拟合良好，具有一定的泛化能力。

4 结 语

鉴于船舶航行过程中的不确定性和非线性，通过应用RBF 神经网络，对船舶横摇运动、垂荡-纵摇耦合运动进行预报研究。 首先，对数据进行误差修正、归一化、正则化等特征工程，在此基础上构造样本集，并将其划分为训练集、交叉验证集和测试集。其次，设计神经网络各层结构及合理选择基函数中心，利用所构造的神经网络对实测数据进行预报测试，验证所应用方法的有效性和可靠性。 研究结果表明RBF 神经网络可以用于有效预报船舶在波浪中的横摇运动、垂荡-纵摇耦合运动。