基于黄金分割的NOMA-SWIPT协作中继网络能效优化算法研究
周宁浩, 侯嘉,2*
(1.苏州大学电子信息学院, 苏州 215006; 2.电子科技大学长三角研究院(衢州), 衢州 324000)
非正交多址接入(non-orthogonal multiple access, NOMA)作为5G(fifth-generation)的核心技术之一,通过利用区别传统时域、频域和空域的功率域思想,针对不同用户分配不同的信号功率,并在接收端采用串行干扰消除(successive interference cancellation, SIC)方法解码对应信号,从而实现有效数据传输[1]。与正交频分复用技术(orthogonal frequency division multiplexing,OFDM)相比,NOMA 允许每个子载波同时服务于多个终端,从而进一步改善频谱效率(spectral efficiency, SE)[2]。近年来NOMA技术广泛运用于车联网[3]、蜂窝网络[4]等通信场景的研究,通过NOMA叠加编码信号传输方案,5G通信环境下的网络性能可以得到提升。
利用功率域的无线携能通信(simultaneous wireless information and power transfer, SWIPT)技术,近年来也在优化能量与信息速率的性能折中问题领域取得了较多的理论成果。SWIPT技术利用无线射频信号既可以传输信息也能够承载能量的特点,通过合理部署传输信号资源,实现了无线通信系统能耗的降低[5],符合“绿色通信”理念。文献[6]提出了在无线能量传输电路中加入可控稳压电路,从而在物理电路角度实现SWIPT的构建。
在能量功率域中对NOMA和SWIPT两种技术进行融合在近期也成了一个研究热点。在系统建模方面,多种NOMA-SWIPT协作中继网络模型被提出,文献[7]建立了简易的单源单中继双用户NOMA-SWIPT网络体系结构,文献[8]则采用双基站双SWIPT中继传输NOMA信号给单一用户。文献[9]提出了经典的三方通信模型,其中近用户既作为接收器接收NOMA叠加信号,也充当SWIPT中继转发信号给远用户。在研究对象与优化目标方面,多数研究将集中于通信网络的中断性能上,研究了能量与功率的资源分配优化方法。文献[10]进一步推导了三方通信网络吞吐量公式,研究在不同网络模式下吞吐量与中继功分因子的关系,并验证了所提出的协作式网络的优越性;文献[11]在推导网络中断概率的同时,对远近用户的分集增益进行了分析,证明SWIPT技术的引入不会影响分集顺序;文献[12]引入路径损耗参数,考虑网络用户传输距离影响,构建了NOMA-SWIPT网络二维拓扑结构并研究受通信距离影响的网络中断性能。在通信工作模式方面,文献[13-14]分别提出了基于半双工和全双工中继的NOMA-SWIPT协作网络协议与架构,并针对中继节点的能量收集与信息转发的问题研究了网络节点在能量和功率域联合优化分配的解决方案,进一步证明了NOMA-SWIPT融合的协作中继网络架构在获得传输性能增益的同时还可以降低系统传输能耗。综上所述,目前学术界的相关研究均验证了NOMA-SWIPT融合的协作中继网络在能量与功率资源优化方面具有较好的前景。
然而,前任研究工作大多是以优化网络中断性能或传输性能为核心目标,而缺乏在采用SWIPT技术的条件下针对系统资源权衡方面的研究。为此,以一个双用户NOMA-SWIPT融合的协作中继网络为例,以保障远端用户的信息接收性能为限定条件,分别从直连模式和中继协作模式角度对整个网络的能量效率(energy efficiency, EE)进行了数学建模,并在此基础上,提出了一种基于黄金分割的DinkelBach能效迭代优化算法(golden section DinkelBach,GS-DinkelBach)。在考虑用户服务质量(quality of service, QoS)、基站发射功率、用户可达速率等约束条件下,与传统直连网络模型和单一中继网络模型进行比较。
1 系统模型
一个由近远端双用户组成的NOMA-SWIPT中继协作网络下行链路模型如图1所示。其中,基站(base station, BS)作为信号发射源,近端用户U1距离基站发射端较近,可作为射频信号能量收集端和中继协作端。
由于远端用户U2距离基站发射端较远,信号接收质量较差,为保障U2的信号接收质量,假设图1中NOMA-SWIPT中继协作网络模型可在工作时隙T内按照时分资源分配规则进行切换,具体如图2所示。
一种是直连模式,工作在直连时隙,长度为T/2,该时隙内BS发送叠加信号x给近远端双用户,近端用户U1接收信号并启动射频信号能量收集功能;当BS至远端用户U2的接收信干噪比(signal to inter-ference plus noise ratio, SINR)大于设定阈值时,近端用户U1不开启中继协作模式,远端用户U2直接接收BS发送的射频信号。
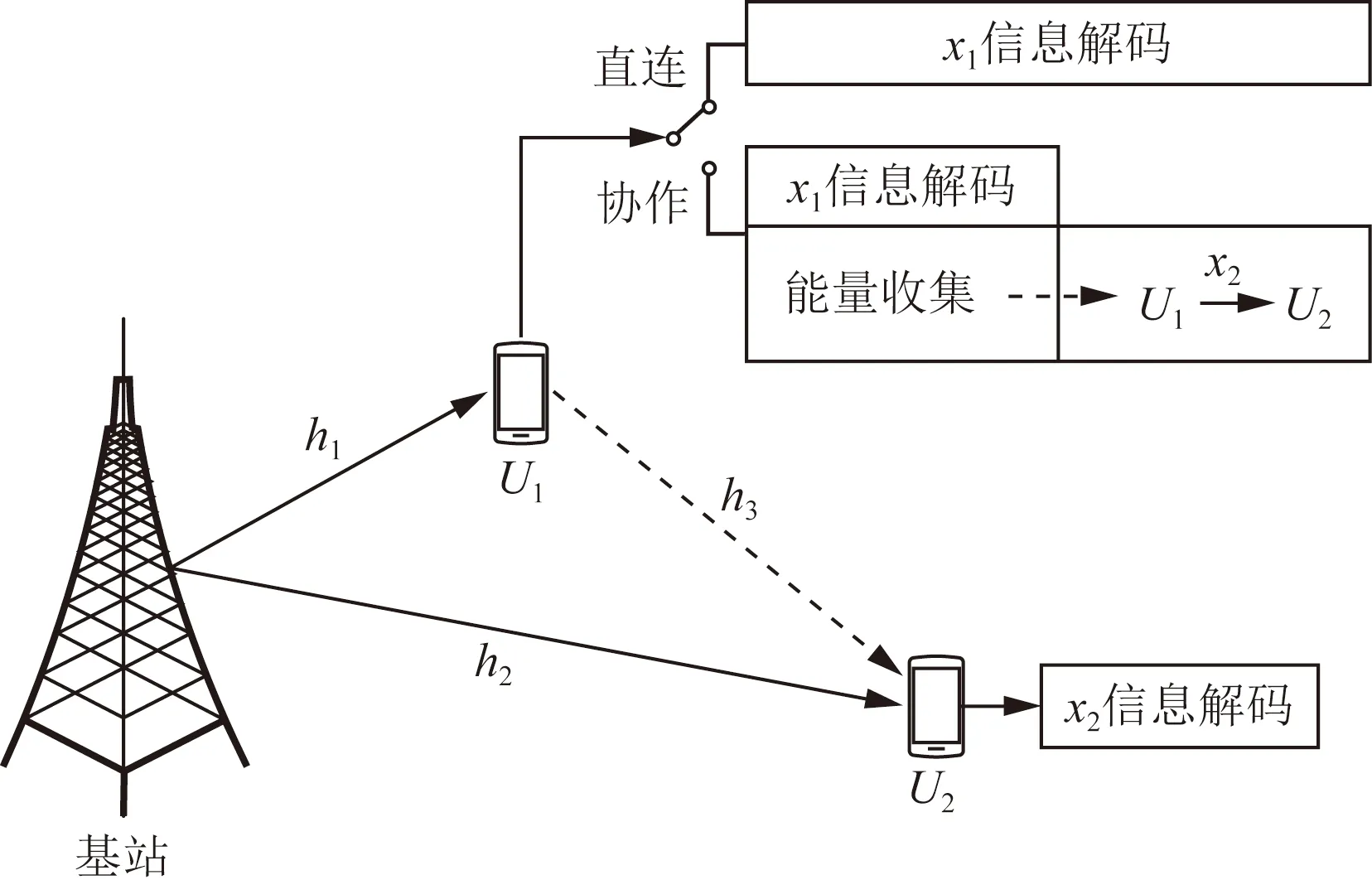
hi为BS到用户Ui的链路信道增益,i=1,2,3;x1和x2分别为近端用户U1、远端用户U2的发送信号图1 下行链路NOMA-SWIPT协作网络Fig.1 Downlink NOMA-SWIPT cooperative network
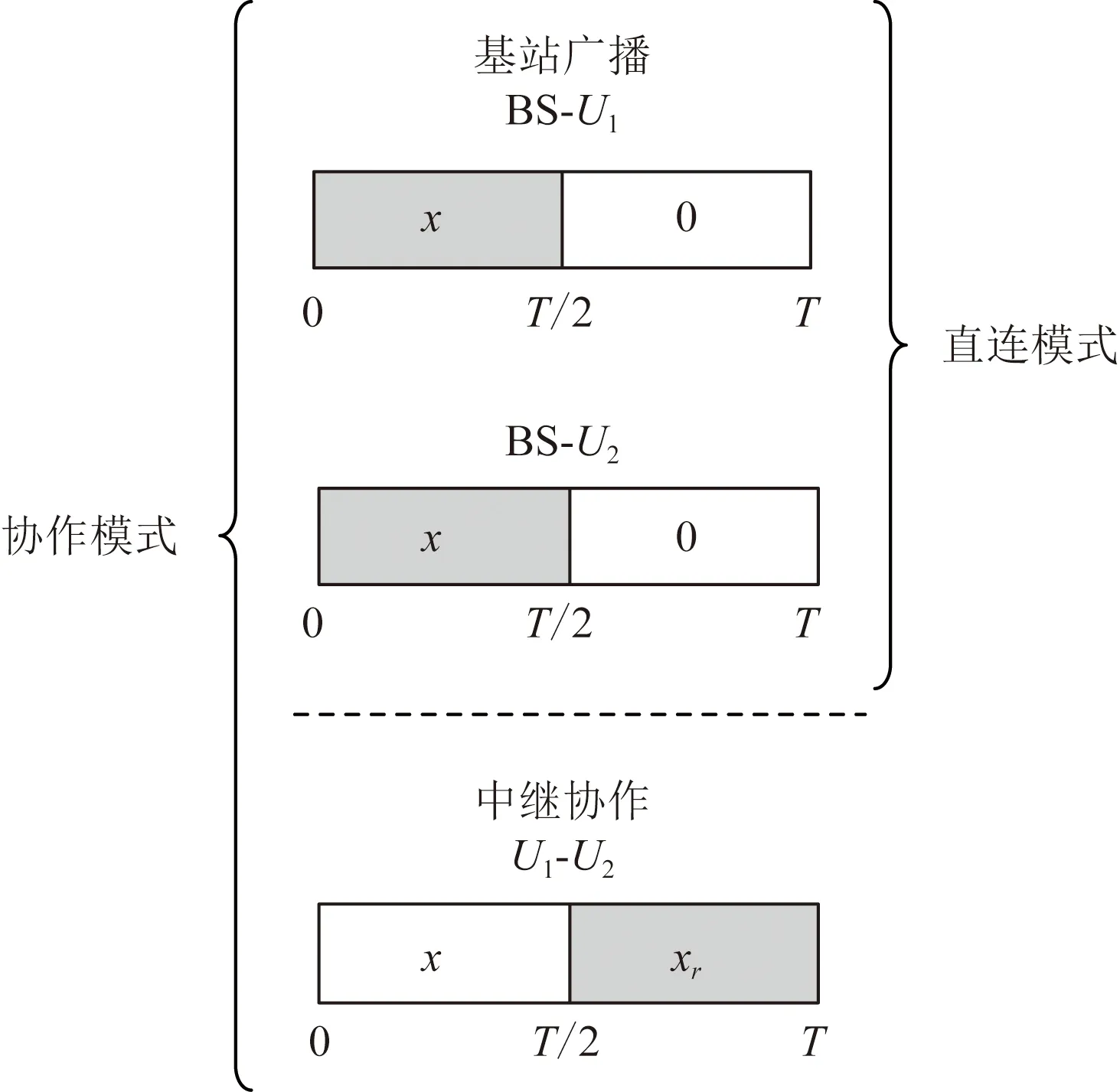
图2 时分资源分配规则Fig.2 Time division resource allocation rule
另一种是中继协作模式,工作在直连时隙结束后,在直连模式的基础上增加了中继协作时隙,其长度也为T/2;当BS至远端用户U2的接收信干噪比SINR小于设定阈值时,近端用户U1开启半双工中继协作模式,在中继协作时隙使用收集到的射频能量转发协作信号xr给远端用户U2。
图1所示的NOMA-SWIPT中继协作网络下行链路中,BS发射的NOMA调制信号可表示为
(1)
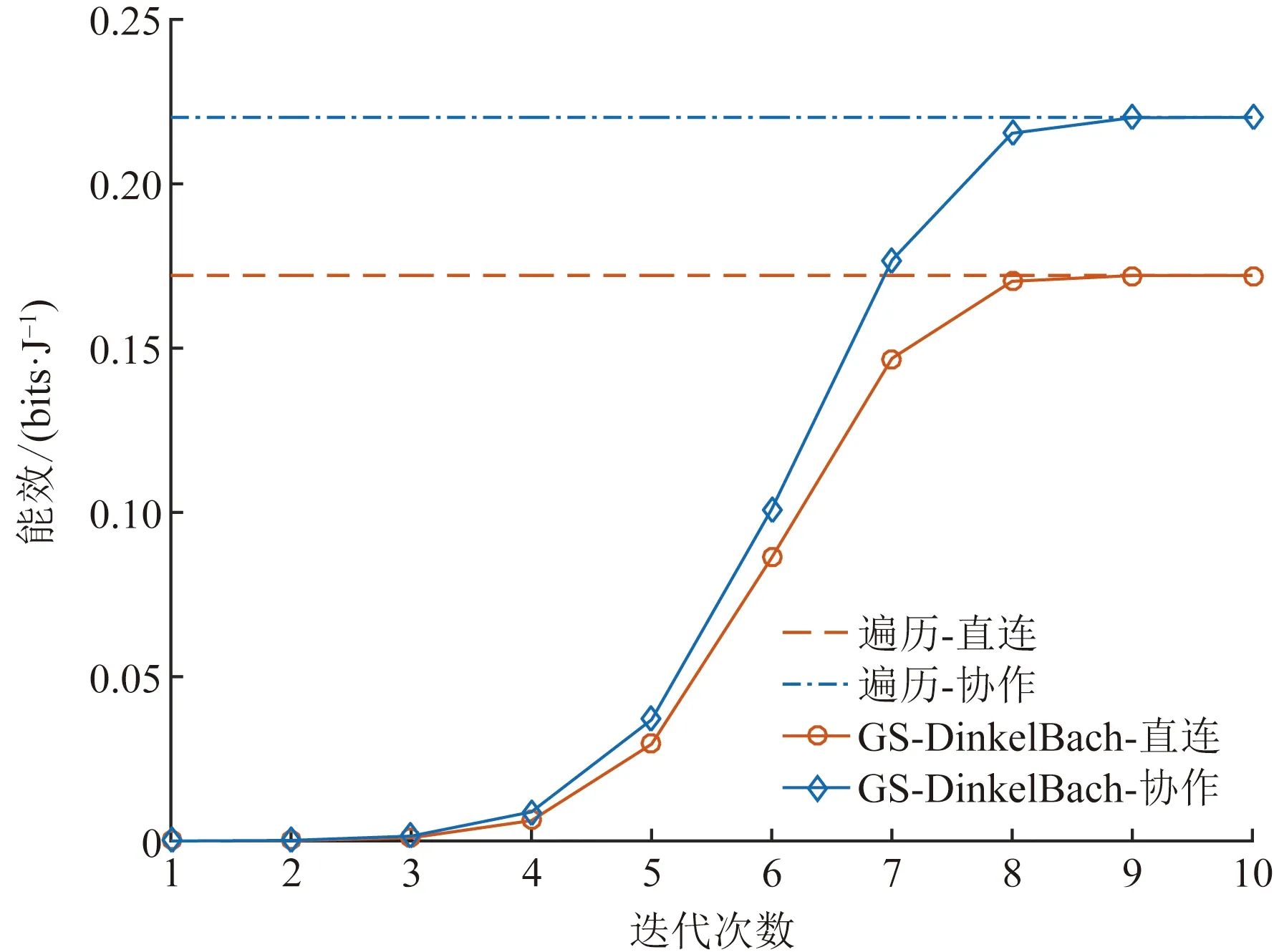
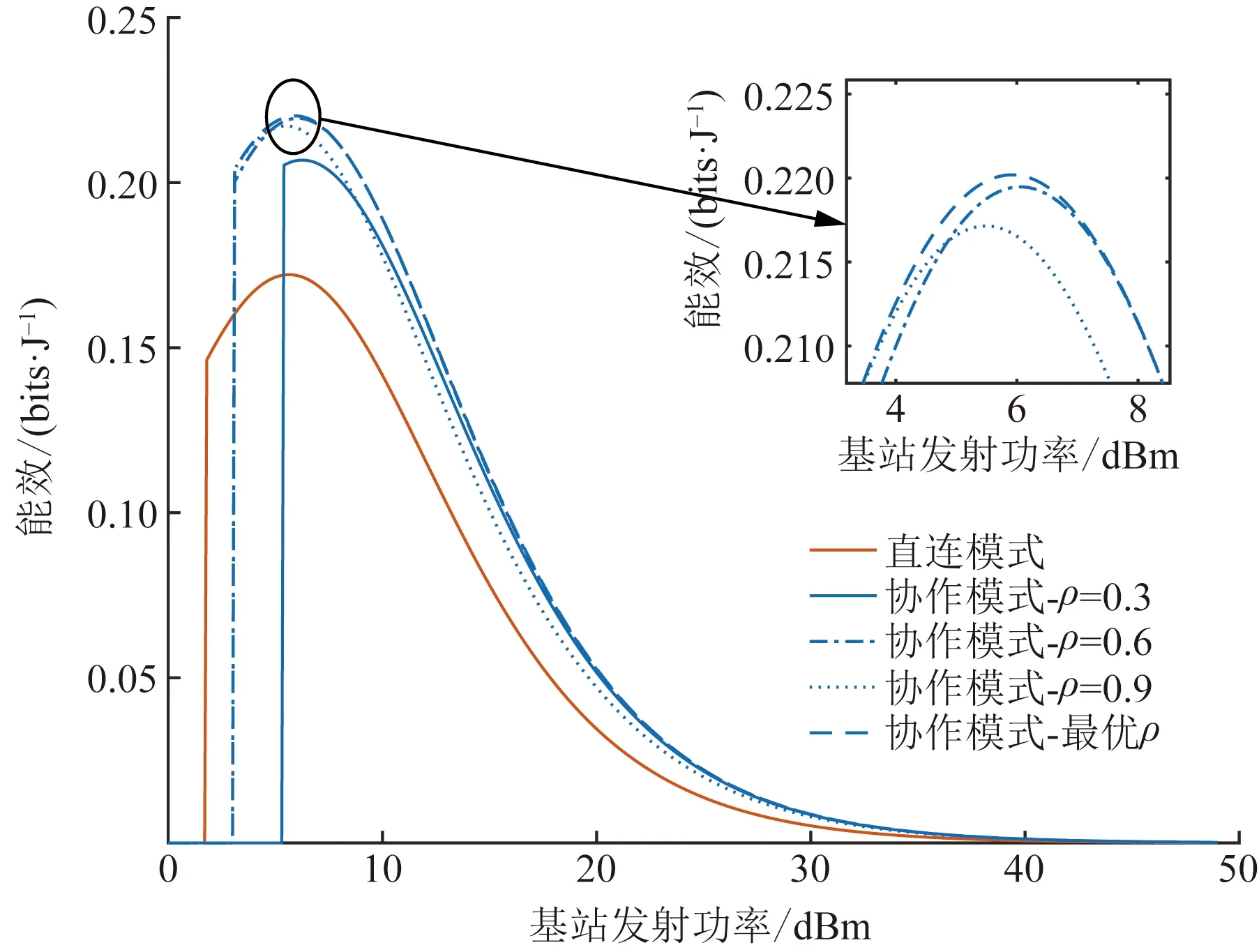
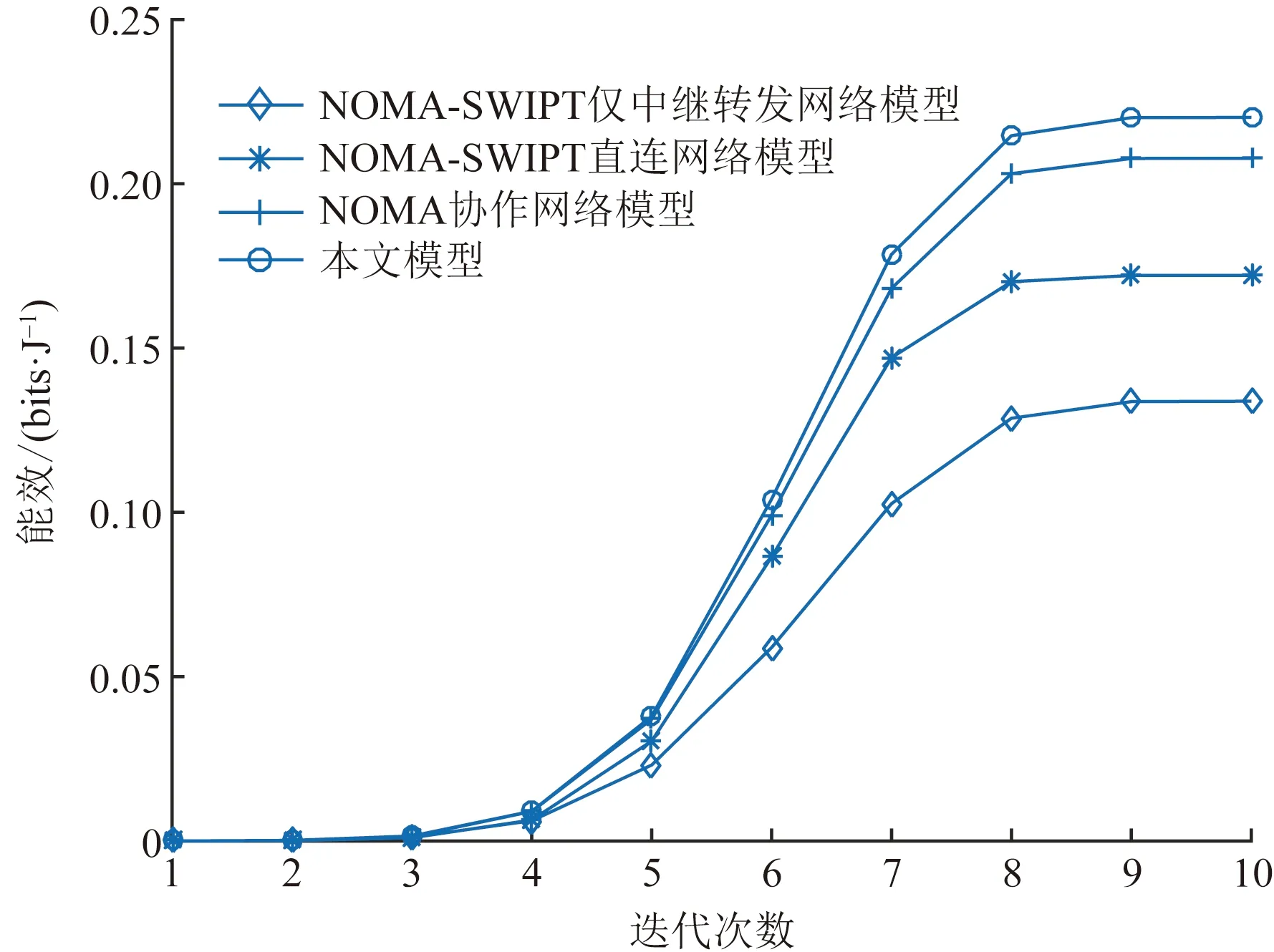
式(1)中:x1、x2分别为用户U1、U2的发送信号,其能量可表示为ε(|x1|2)和ε(|x2|2);a1、a2为NOMA调制的功率分配系数,且0 BS发射信号的总能量可定义为 Ps=a1ε(|x1|2)+a2ε(|x2|2) (2) 工作在直连模式时,用户Ui的接收信号可表示为 yd,Ui=hix+ni (3) 式(2)中:hi为BS到用户Ui的链路信道增益;ni为对应通信链路下的加性高斯白噪声(additive white Guassian noise, AWGN),ni~CN (0,σ2),i=1,2,其中σ2为噪声方差,即噪声功率。 近端用户U1的能量收集采用功分器实现,其功率分配因子为ρ,因此U1处收集的能量可表示为 Pr=ηρ|h1|2Ps (4) 式(3)中:η为U1作为接收机的能量转换效率。 用于用户检测的信号可表示为 (5) 假设通过基于NOMA信号检测算法SIC,用户U1可以正确解出x1和x2。 当远端用户U2接收到的信号较差且小于设定阈值时,NOMA-SWIPT中继网络切换工作到中继协作模式。此时,近端用户U1开启中继转发功能,转发信号的能量为收集到的射频信号能量,即 ε(|x′2|2)=Pr (6) 式(6)中:x′2为近端用户U1解码转发的信号,因此U2在中继协作时隙收到信号为 yc,R=h3x′2+n3 (7) 式(7)中:n3为对应通信链路下的加性高斯白噪声,n3~CN(0,σ2);h3为转发链路的信道增益。 在中继协作模式下,U2两个时隙接收到的联合信号可表示为 (8) 根据提出的网络模型与时分资源分配规则,由于用户U1在网络直连模式与协作模式下的功能不同,因此网络中3条通信链路的通信可达速率也将受到影响,如表1所示。根据远近端双用户系统模型可知,g1>g3>g2且Rd,2 (9) 直连模式下,网络仅进行BS-U1、BS-U2两条链路通信,根据表1,网络直连模式能效方程可表示为 (10) 式(10)中: (11) (12) 表1 不同模式下链路可达速率Table 1 Achievable rates of links in different modes P1和P2分别为采用NOMA技术的近用户U1与远用户U2的分配功率,Ps=P1+P2。因此直连模式网络能效优化问题可表示为 (13) 式(13)中:Rmin为不同通信链路下的最小信道容量约束;Pmin为基站最小发射功率约束,约束需满足QoS条件,保证网络的正常通信。 直连模式下网络能效的主要影响因素为基站发射功率Ps,因此能效最大化问题可被视为基站发射功率问题,是典型的分式规划问题,采用DinkelBach算法[15]实现能效最大化。 (14) 因此,经过DinkelBach算法修正的能效优化问题为 (15) 令目标函数为F(Ps),易证F″(Ps)<0,因此目标函数为凹函数,具有单峰性,可以通过黄金分割法[16]降低最优值搜索复杂度,黄金分割方法可以通过比较探点所在函数值不断更新探点,作为类似于传统二分法的一种算法,其复杂度远低于等间隔搜索。 设[αn,βn]为变量可行搜索区间,如果探点λn处的函数值大于探点μn处的函数值,则更新搜索区间为[αn+1,βn+1]=[αn,μn];反之则更新搜索区间为[αn+1,βn+1]=[λn,βn]。 探点的选择满足 βn-λn=μn-αn (16) βn+1-αn+1=γ(βn-αn) (17) γ为更新区间与原区间的长度比例,将式(16)、式(17)联立,可得 λn=αn+(1-γ)(βn-αn) (18) μn=αn+γ(βn-αn) (19) 设此时目标函数f(λn)>f(μn),则βn+1=μn,因此有 μn+1=αn+1+γ(βn+1-αn+1) =αn+γ(μn-αn) =αn+γ(αn+γ(βn-αn)-αn) =αn+γ2(βn-αn) (20) λn=αn+0.382(βn-αn) (21) μn=αn+0.618(βn-αn) (22) 采用黄金分割方法的改良型DinkelBach能效迭代优化算法实现步骤如表2所示。 表2 基于黄金分割的DinkelBach能效迭代优化算法Table 2 Proposed GS-DinkelBach energy efficiency iterative optimization algorithm 定义协作模式是在直连模式通信的基础上,增加U1-U2通信链路,因此考虑的参量更加的复杂。网络协作模式能效方程为 (Ps+Pc+ηρg1Ps-ηρg1Ps)-1 (23) 式(23)中:PEH为用户U1在网络作为SWIPT中继时从BS-U1链路收集的能量;PCR为协作模式下U1向U2转发信息时的发射功率,不考虑收集能量—信息转发过程中的额外损耗,即中继收集的能量完全转化为U1-U2的发射功率,因此有PCR=PEH=ηρg1Ps。 可以看出,这一模式下的网络能效不仅受基站发射功率Ps影响,同时也受到SWIPT中继(协作模式下的用户U1功分因子ρ的影响,因此能效优化问题可表示为 (24) 式(24)中:Rimin为通信链路最低可达速率;Emin为近端用户(即中继)能量接收最低门限值;Pmin为基站最小发射功率。 协作模式相比直连模式不仅优化参数增多,考虑的QoS约束条件也更加全面(Rimin、Emin、Pmin、ρ)。对于双参数优化问题,可以多次使用GS-DinkelBach算法来执行双层迭代,但同时也会提升计算复杂度。通过计算固定基站发射功率Ps下最优中继功分因子ρ并将其用当前Ps表示,再针对更新后的问题求最优能效,从而实现将双层迭代转换为单层迭代的过程。 (Ps+Pc+ηρg1Ps-ηρg1Ps)-1 (25) =Aρ2+Bρ+C (26) 式(26)中: (27) (28) (29) 不难得出,固定Ps条件下最优ρ值ρ*与最优Hopt分别为 (30) Hopt=H(ρ*) =H*(Ps) (31) 针对式(30)、式(31)化简后的问题式(25),通过表2中的迭代算法即可求得能效最优值。 对提出的能效优化问题和算法进行仿真和数值分析,从而验证提出的NOMA-SWIPT中继协作网络和GS-DinkelBach迭代算法的优越性。 仿真中将信道噪声视为加性高斯白噪声,功率σ2=0.5 W;采用NOMA技术的基站功分因子α=0.2,其中,P1=αPs,P2=(1-α)Ps;用户U1作为SWIPT中继时的能量收集效率η=0.7[11];BS-U1、BS-U2、U1-U23条通信链路的信道功率增益分别为g1=0.7,g2=0.2,g3=0.5;网络运行时的总电路损耗Pc=2 W。设定的系统参数仅为计算本文网络能效,可以根据特定模型进行相应的修改。 图3显示了所提出的GS-DinkelBach迭代算法的优越性。在仿真中,将所提出算法的迭代曲线与遍历方案进行了比较,以证明算法的收敛性和结果的准确性。通过该算法,两种模式下的网络能效均通过10次迭代达到最佳值。 将GS-DinkelBach算法与传统DinkelBach算法比较,GS-DinkelBach算法的计算复杂度为O[10log1/0.618(N)],传统DinkelBach算法计算复杂度为O(10N),其中O为算法计算复杂度的表征,由此可见GS-DinkelBach算法具有较低的计算复杂度,且优越性随着Ps搜索步数N的提升而越发显著。 图4展示了基站发射功率Ps对于网络不同模式下能效指标的影响曲线。可以看出,受QoS等约束条件影响,当Ps取值无法满足阈值要求时网络能效均为0。在满足约束条件的前提下,随着Ps增大,网络能效会达到一个峰值,即为固定中继功分因子条件下的最优能效。 网络能耗作为能效方程分式分子,对于整体网络性能的影响随着Ps继续增加而越来越大,因此曲线在达到峰值后会呈下降趋势并逐渐趋向于0,整体曲线呈现单峰特性。 由图4可知,网络直连模式下的能效总是低于协作模式,由此可以证明提出的NOMA-SWIPT协作网络优越的能效性能。表3统计了网络协作模式下受不同中继功分因子影响的最优能效,分析可知,功分因子的变化与最优能效并不成正比,因此有必要针对网络发射功率和功分因子进行联合优化。 图3 网络能效迭代曲线Fig.3 Network EE iteration curves 图4 基站发射功率与网络能效的性能分析Fig.4 Performance analysis of BS transmit power and EE 表3 协作模式下中继功分因子对应能效统计Table 3 Corresponding energy efficiency statistics of relay power splitting factors in cooperative mode 图5的仿真工作主要是对比不同系统模型的网络性能。可以看出,所构建的NOMA-SWIPT协作中继网络模型具有较高的性能优势,即相同参数下更高的网络能效。当采用NOMA协作网络(无SWIPT)模型时,中继不再具有能量收集技术,因此网络能耗增大,性能降低。而对比NOMA-SWIPT直连网络模型和仅采用近用户充当中继通信的协作网络(无直连)模型,构建的模型依旧具有能效性能好优势,原因在于两种模型并未最大化利用基站提供的信息与能量。 由GS-DinkelBach算法获得的能效增益统计如表4所示。可以看出,本文模型的最优能效值远优于直连网络和中继转发网络,能效性能分别提升了1.07、2.17 dB,相较于NOMA协作网络(无SWIPT)等传统模型也具有一定的能效增益。此仿真证实了将NOMA、SWIPT和中继技术融合的优势。 图5 不同系统模型能效性能分析Fig.5 Energy efficiency performance analysis of different system models 表4 不同网络模型的最优能效Table 4 Optimal energy efficiency in different network models 建立了一个NOMA-SWIPT协作中继网络,并提出了一种时分资源分配方法。根据网络特征,列出了直连模式和协同模式下的网络能效优化问题,并采用GS-DinkelBach迭代算法,以实现最优网络能效。仿真和数值结果表明,GS-DinkelBach迭代算法能够以较低的计算复杂度获得准确而可观的能效增益。此外,本文模型具有比传统模型更好地能效性能,这证实了NOMA,SWIPT和中继技术的集成系统具有性能优势。2 能效优化
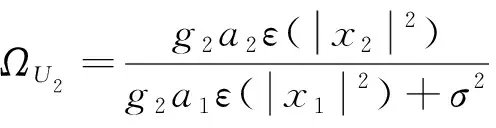
2.1 直连模式网络能效分析
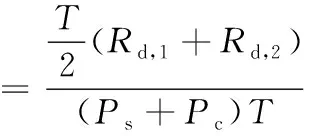
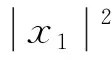
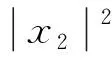

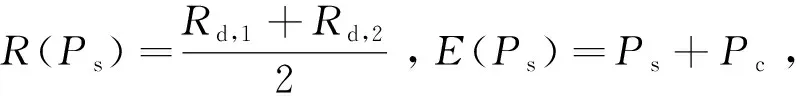
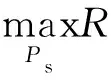
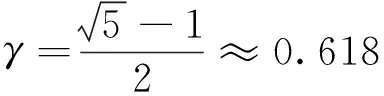

2.2 协作模式网络能效分析

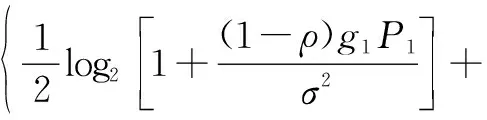
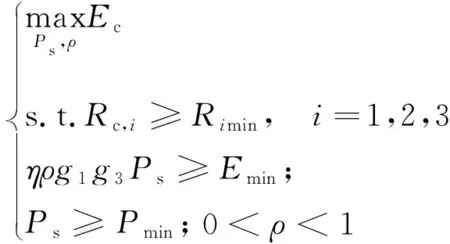

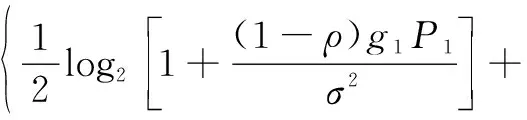
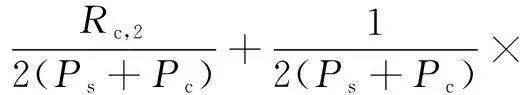

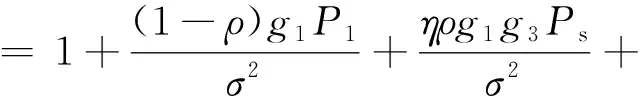
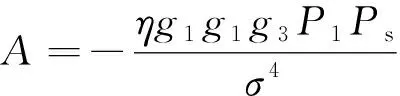
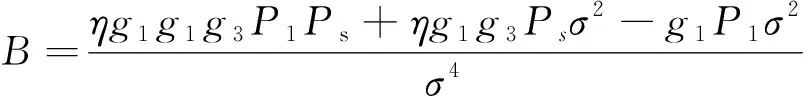
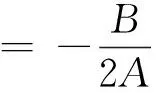
3 仿真结果与分析


4 结论

