基于增广拉格朗日交替方向非精确牛顿法配电网电源机会约束分布式控制

闫佳文， 周磊， 郑焕坤， 陈长金， 蒋春悦

(1. 国网河北省电力有限公司培训中心， 石家庄 050000； 2. 北京科东电力控制系统有限责任公司， 北京 100192；3. 华北电力大学(保定)电力工程系， 保定 071003)

分布式电源(如光伏阵列、恒温控制负载和储能装置)的大量接入正在改变配电网的特性。配电网不再是高压输电网和电力终端用户之间的中介网络，而是可以利用分布式电源，通过为输电系统提供服务和实现精细化电力输送，降低其运营成本，并有所盈利的电网中独特的结构单元[1-5]。这种转型成功与否取决于能否有效处理分布式电源如光伏的高波动性、提升其可控性以及能否将配电系统中的潮流和电压幅值维持在一个可以接受的范围。研究在符合配电系统中的潮流和电压限制的条件下,与逆变器相连的电源(如光伏阵列、恒温控制负载、储能装置)的控制策略，来为配电网提供足够的调度灵活性。

分布式电源在技术上可以同时为配电网和输电网提供服务[6-7]。但是两者有明显区别。首先，在输电网中提供电网支持服务通常是集中式电源，并要求集中式电源达到一定的标称容量。这一要求使分布式电源失去了在输电网直接提供服务的资格。相反，配电系统运行的层级较少，允许小规模电源参与电网的运行。为了使来自分布式电源的能量输出达到一定规模来改变系统的运行特性，迫切需要设计分布式电源的控制策略。分布式方法的主要特征是分布式电源可以根据本地电气量的测量结果对配电网中不断变化的运行条件做出反应，而无需集中式调度中心的参与[8]。

Turitsyn[9]提出并比较了一组逆变器的分布式控制策略，用以控制电压和最小化潮流损耗，其仿真结果表明，同时控制电压和最小化损耗的混合控制策略比单目标控制策略中的任何一种更为有效。Hashim等[8]研究表明，任何控制策略的效果都会随着输入测量次数(有功功率、无功功率、电压幅值)的增加而提高。Turitsyn等[10]和Kundu等[11]将文献[9]的控制策略应用到配电网最优潮流中，并比较了集中式和分布式两种运行方式对配电网运行成本的影响。尽管集中式的运行成本略低，但它需要一个与分布在各地的电源通信的信息中心，现实情况下这难以做到并易受恶意的网络攻击。相反，分布式方法不需要通信，能够在满足潮流和电压约束的条件下运行系统[11]。Sulc等[12]在文献[9]控制策略上通过允许相邻分布式电源之间的通信来运行系统，相邻分布式电源之间的通信进一步降低了分布式方法下运行系统的成本，求解算法采用的是交替方向乘子法(alternating direction method of multipliers，ADMM)[13-15]。

对于分布式求解算法， ADMM方法并不能保证在足够多次的迭代后收敛。大量算例表明，只有在参数合适的情况下应用ADMM算法才会收敛。针对这一问题，增广拉格朗日交替方向非精确牛顿法(augmented Lagrangian alternating direction inexact Newton method, ALADIN)算法被提出，与ADMM算法相似的是，在每一次迭代中，分布式个体求解自身的解耦问题，然后由计算中心求解一个集中式优化问题，与ADMM不同的是，ALADIN算法能保证在足够多次的迭代后收敛[16-17]。

综上所述，以往研究控制策略的设置以节点位置的功率输出值为基础，并未考虑潮流的测量值，所采用的分布式算法也不能保证收敛。因此本文基于分布式逆变器连接点处的潮流的测量值，以配电网最优潮流为目标设计控制器。然后将这一策略整合到如文献[12]中的有限通信的分布式潮流优化中，并利用机会约束描述光伏注入功率的不确定性。机会约束方法已经在输电网[18-20]和配电网[21]中的不确定性潮流优化中得到了应用。使用机会约束的目的是用凸约束来描述光伏电源出力的随机性，进而采用凸优化算法精确求解。所提出的机会约束分布式潮流优化通过ALADIN求解。算例仿真在IEEE 33节点配电网系统进行，对提出的集中式和分布式的控制策略予以对比分析。

1 逆变器的分布式控制策略

1.1 逆变器模型

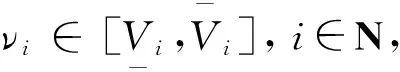
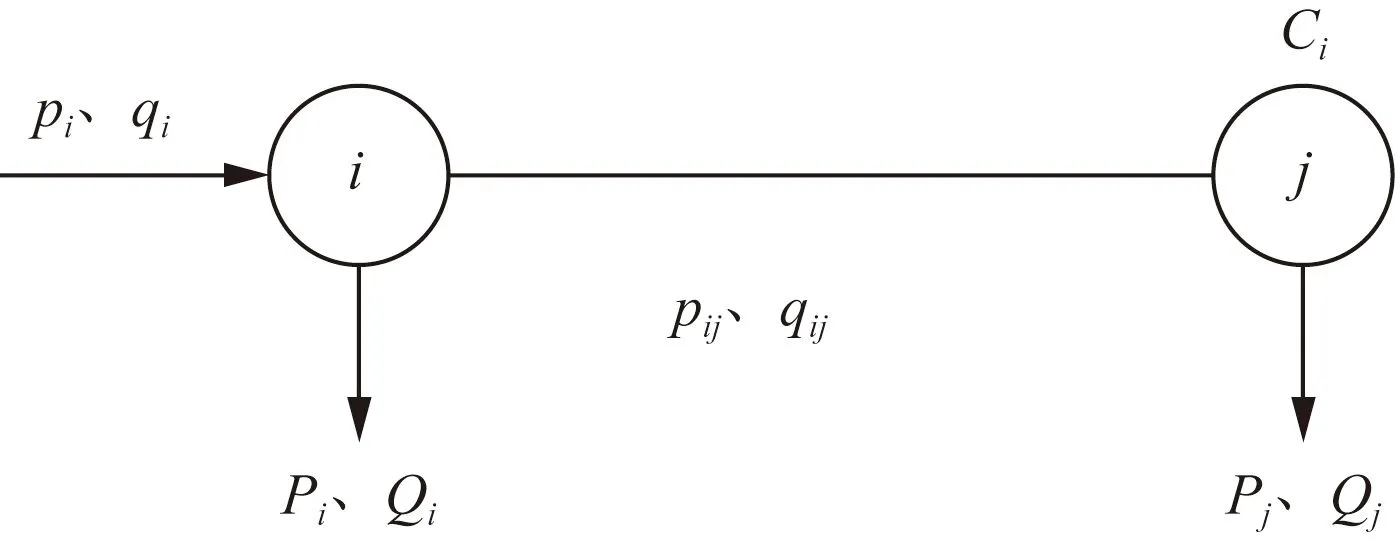
图1 一个有两个节点的辐射状系统Fig.1 A two-bus radial system

(1)

(2)

uj=ui-2(Rijpij+Xijqij), ∀i,j∈ε

(3)

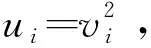
光伏电源的有功功率和无功功率输出受到逆变器额定功率的约束为

(4)

(5)

因为分布式电源逆变器输出的无功功率在式(5)给出的范围内大小可调，可以以此为控制变量采用合适的控制策略来实现配电网的电压支持和潮流损耗最小化。

1.2 现有控制策略

回顾现有的控制策略，根据其控制目标归纳如下。

1.2.1 恒定功率因数

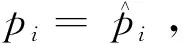
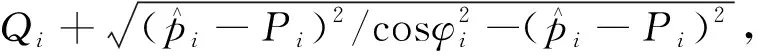
∀i∈NPV

(6)

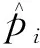
需要注意的是，在某些情况下，恒功率因数策略可以放宽，即允许功率因数维持在给定的范围内，而不是定值[22]。在实践中，恒功率因数策略已经被证明是有效的，可以将节点电压保持在允许的范围内[8]。然而，随着逆变器数量的增加，这种策略的控制效果明显下降。

1.2.2 电压控制

在分布式逆变器的控制策略中重点考虑控制电压[23]。文献[9，23-24]研究了基于sigmoid函数的这种控制策略，其中控制规则为

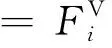
(7)

相对于控制策略[式(6)]，控制策略[式(7)]更为有效，因为它的控制目标在于节点电压。但在某些情况下它会增加系统功率损耗，通常认为它的控制成本较高[9]。

1.2.3 功率损耗最小化

Sulc等[25]提出了潮流损耗最小化的控制策略，可表示为

∀i∈NPV

(8)

与式(7)的控制策略相反，潮流损耗最小化的控制目标可能会使有些节点的电压越限。

1.2.4 混合策略

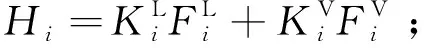
2 动态潮流控制策略

2.1 集中式动态潮流控制策略

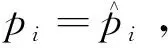
(9)

(10)

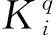
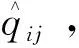
式(9)中的控制是基于无功功率的测量，该控制也可以扩展到有功功率的测量。此情况下，逆变器的有功功率和无功功率输出的控制方法为

(11)

(12)

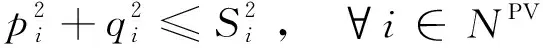
(13)

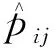
式(12)改变了节点i处逆变器的有功功率输出。式(13)给出了pi和qi的可行域。由于光伏电源的有功功率输出是不确定的，也不能保证其可以按需增加，因此式(12)中的控制策略需要与同一节点i的储能相协调。

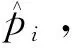
2.2 机会约束分布式动态潮流控制策略

为了反映所提出控制策略的在配电网电源实际运行的分布式特性，并且确保分布式算法在多次迭代下能够收敛，首次引入ALADIN分布式算法[17]用来求解所构建的问题。最后，使用机会约束对问题进行了扩展，使其可以描述光伏电源出力的不确定性[26]。

2.2.1 分布式最优潮流问题

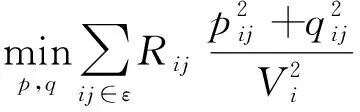
(14)

式(14)中：Vi为节点i的电压值；Rij为线路ij段的电阻值；p为节点注入有功功率；q为节点注入无功功率。

由于LinDistFlow忽略了辐射状配电网潮流方程的二阶项，式(14)根据潮流pij和qij的近似值计算近似功率损耗。为了采用分布式方法ALADIN算法处理这个问题，对式(14)、式(15)调整如式(11)～式(13)及式(15)～式(21)所示。

(15)

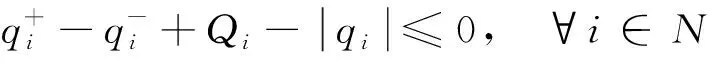
(16)

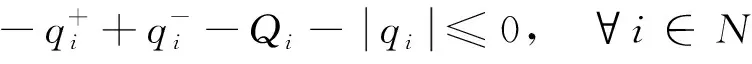
(17)

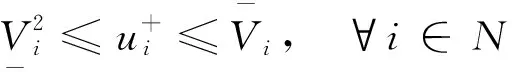
(18)

(19)

(20)

(21)

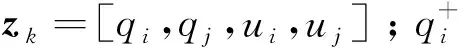
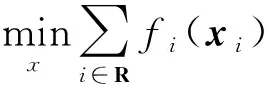
(23)

(24)

hi(xi)≤0|κi， ∀i∈R

在互联网这一个大背景下，一个高校教学目标的制定是十分重要的，而现如今，各大高校在教学目标的制定上都存在着一些或多或少的问题，所以，各大高校在教学目标的制定中，需要考虑的一个比较重要的问题就是，想出一个办法，如何让教师不再是知识的传递者，让学生不再是知识的收藏者，并且如何让学生变为知识的创新者。所以，为了完成这个教学目标，在教学中，充分利用互联网的优势，我们要为学生提供足够的信息资源，让学生们对学习产生浓厚的兴趣，让学生们可以积极主动地去获取知识，使学生们成为学习的主体，高校将教学目标以及教学内容和教学评价标准告诉学生，帮助学生树立正确的学习方向以及为学生学习目标的制定提供借鉴。

(25)

(26)

表1 配电网最优潮流Table 1 Optimal distribution optimal power flow

2.2.2 算法流程

基于ALADIN算法的配电网最优潮流算法流程如表1所示。

2.2.3 光伏不确定性建模

在提出的分布式最优潮流问题中，可以采用机会约束方法描述光伏出力的不确定性。由文献[18-19]机会约束方法可得

(27)

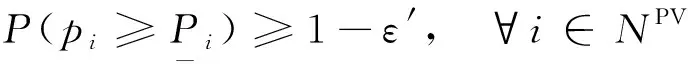
(28)

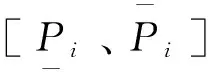
因此，式(16)和式(17)修改为

(29)

(30)

式中：P为括号内式子成立的概率计算；tanφi为常数。

2.2.4 机会约束处理方法

设ξ～N(μ,σ)为随机变量的向量，其均值和方差分别由向量μ和σ给出，设b和x分别为参数和决策变量的向量。机会约束为

P(ξTx≤b)≥1-ε′

(31)

可以用以式(32)表示。

(32)

式中：ε′∈[0，1]为对违规行为的容忍度；Φ-1为标准正态分布的逆累积分布函数。

式(32)可以等价地用式(33)、式(34)约束条件代替。

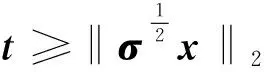
(33)

μTx+Φ-1(1-ε′)t≤b

(34)

式中：t为新定义的变量。

上述转换是由JumpChance这个Julia包自动完成的[27]。

3 算例仿真

3.1 集中式动态潮流控制策略仿真

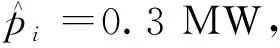
图3显示了下垂系数K不同的值下，所提策略是如何改变配电网中的总有功功率损耗的，并将其

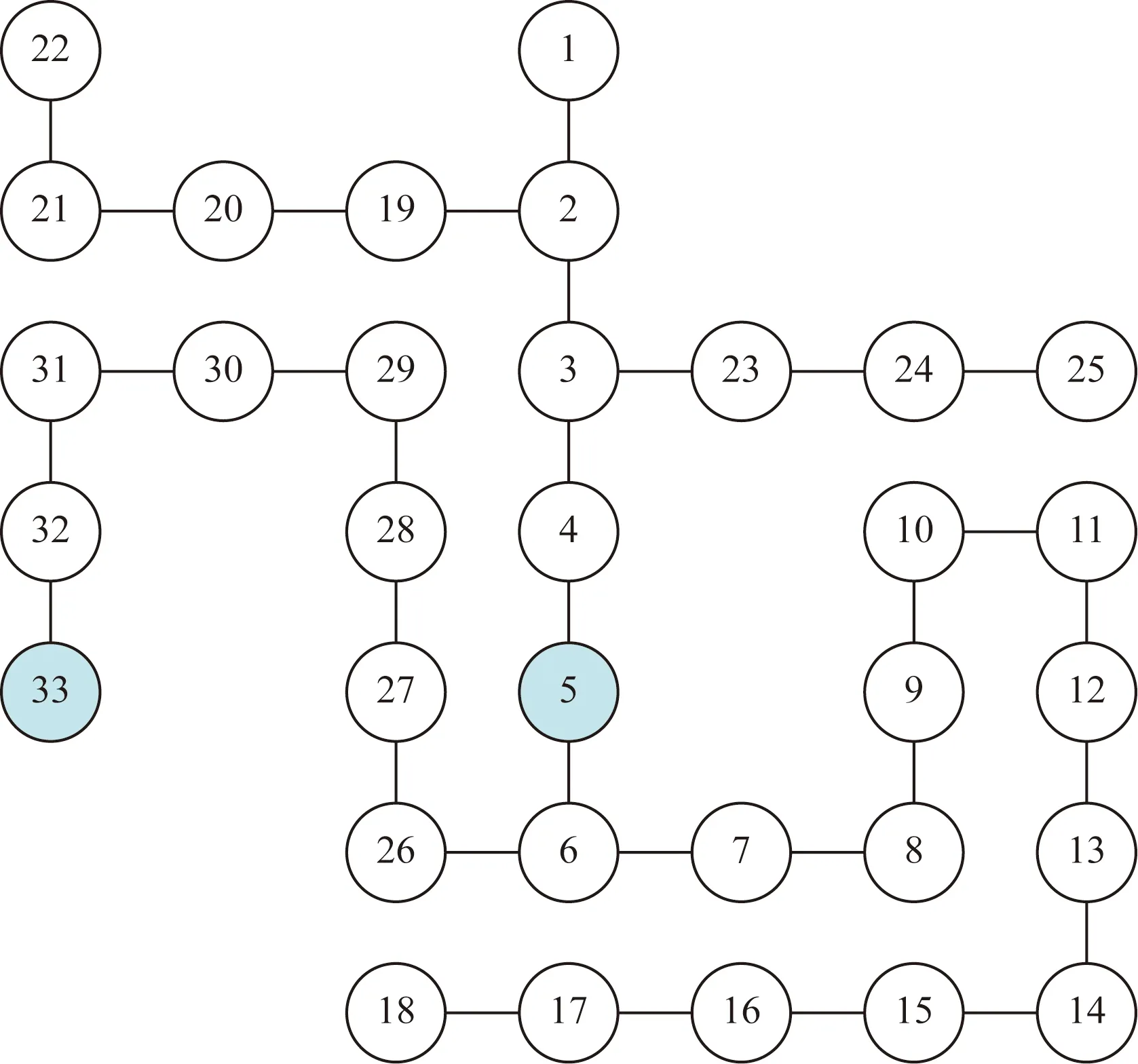
图2 IEEE 33节点配电系统Fig.2 IEEE 33-bus distribution system

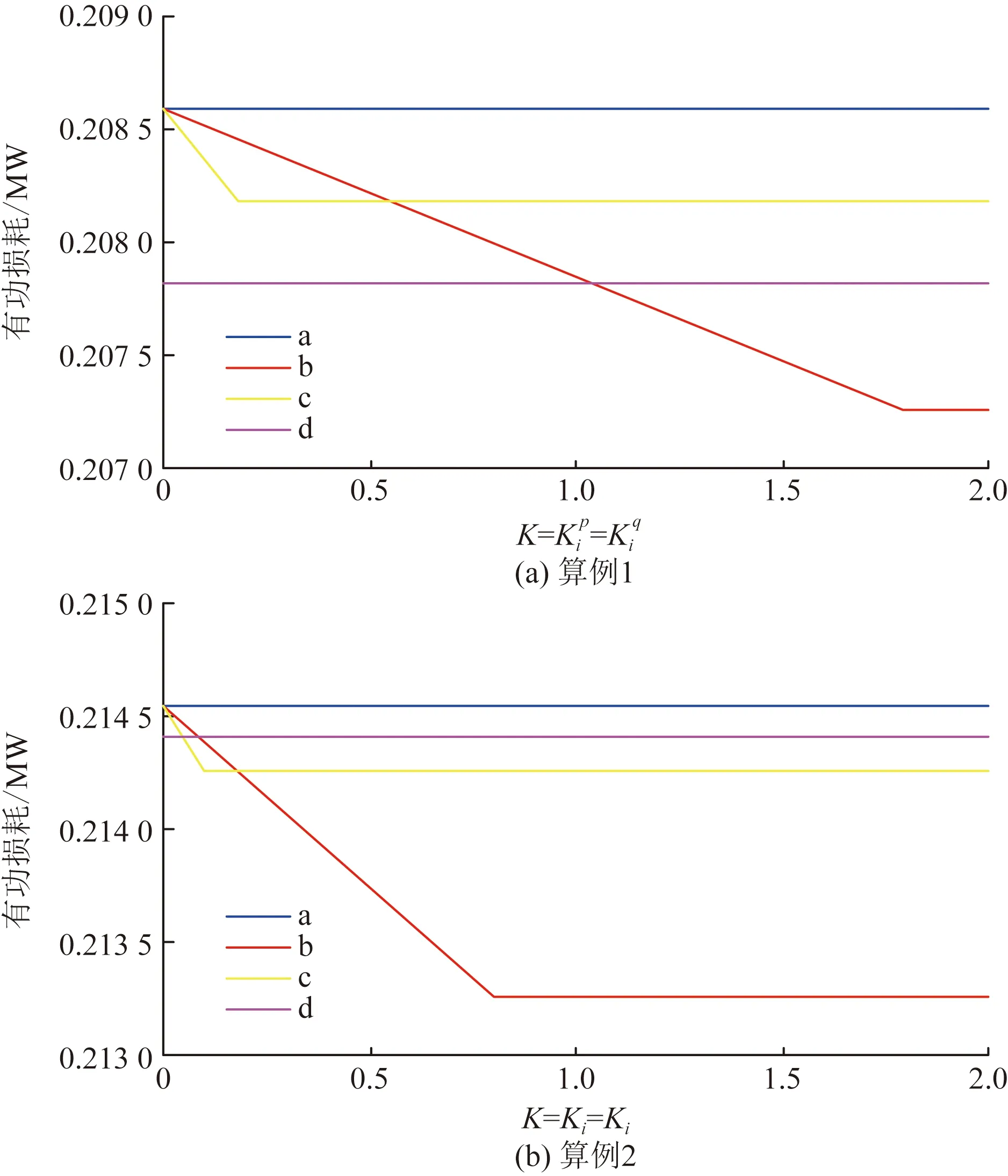
a为无控制；b为式(11)～式(13)中的控制策略；c为式(9)和式(10)中的控制策略；d为式(8)中的图3 配电网总有功功率损耗比较Fig.3 Comparison of total active power loss in distribution network

与没有基于逆变器的任何控制的情况和采用式(8)中的功率损耗最小化控制策略进行比较。仿真结果显示相对于没有启用基于逆变器的控制的情况，使用任何控制策略都能降低损耗。在这两种工况下，所提出的策略相对于式(8)对下垂系数K的值更为敏感，随着K值的增加，所提出的策略变得更有优势。关于下垂系数K的取值，所提出的策略对较高的K值线性降低损耗，直到逆变器的输出达到额定功率S，产生如图3所示的转折点。在转折点之后，增加K的值不会导致任何额外的功率损耗降低。与式(9)和式(10)中的控制策略相比，式(11)和式(13)中的控制策略同时调节逆变器的有功功率和无功功率输出，在较高的下垂系数K值下会达到饱和，从而导致更多的功率损耗降低。

3.2 机会约束分布式动态潮流控制策略仿真

在IEEE 33-bus配电系统上执行所提出的分布式潮流机会约束配电网最优潮流方案，其中光伏电源分别安装在2号节点(1.9 MW)、3号节点(3.77 MW)、6号节点(7.54 MW)、18号节点(1.88 MW)、21号节点(4.71 MW)、25号节点(4.24 MW)和32号节点(5.94 MW)，如图4所示。各个光伏电源处的预测误差的均值为零，预测误差变化范围为预测值的10%。在下面的仿真中，对于所有的机会约束条件，统一设置ε′的值。将提出的分布式优化与确定性集中式(全局)优化进行比较。

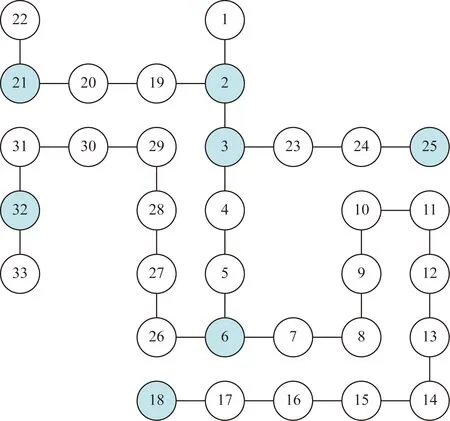
图4 IEEE 33节点配电系统Fig.4 IEEE 33-bus distribution system

3.2.1 功率损耗

图5、图6显示了分布式逆变器的总无功功率注入和全系统有功功率损耗方面的ALADIN收敛情况。尽管该算法在所有考虑的实例中收敛所需的迭代次数不超过130次，但在两张图中都有明显的峰值。这些尖峰的特征是，当逆变器以额定容量运行，不能再为系统提供无功功率支持时，就会出现类似图3的转折点。随着ε′的增加，即机会约束越来越严格，分布式逆变器的总无功功率注入量单调增加。这说明所提出的控制策略和分布式优化对于更严格的运行更有优势。在所有机会约束都满足的情况下，全系统的有功功率损耗大致保持不变。对于全系统有功功率损耗来说，无论选择的ε′值是多少，所提出的分布式优化的效果都特别明显，相对于确定性集中情况来说，都会大幅度降低。

3.2.2 节点电压

将ε′的值设为0.05，并跟踪各分支的电压曲线，如图4所示。图7和图8分别详细列出了分布式和集中式情况下各分支的电压曲线，图9则逐项列出了两种情况下分布式逆变器的节点无功注入量。在集中式情况下，所有分支的电压曲线单调降低。分布式优化的效果是双重的。首先，与集中式情况相比，它缩小了各分支起点和终点电压幅值之间的差距，部分分支间的电压曲线不是单调的。从图7可以看出，支路C、E、G、F有电压尖峰，这些尖峰是由分布式逆变器的无功注入引起的。这些尖峰是由分散和集中情况下不同的无功注入引起的，如图9所示。

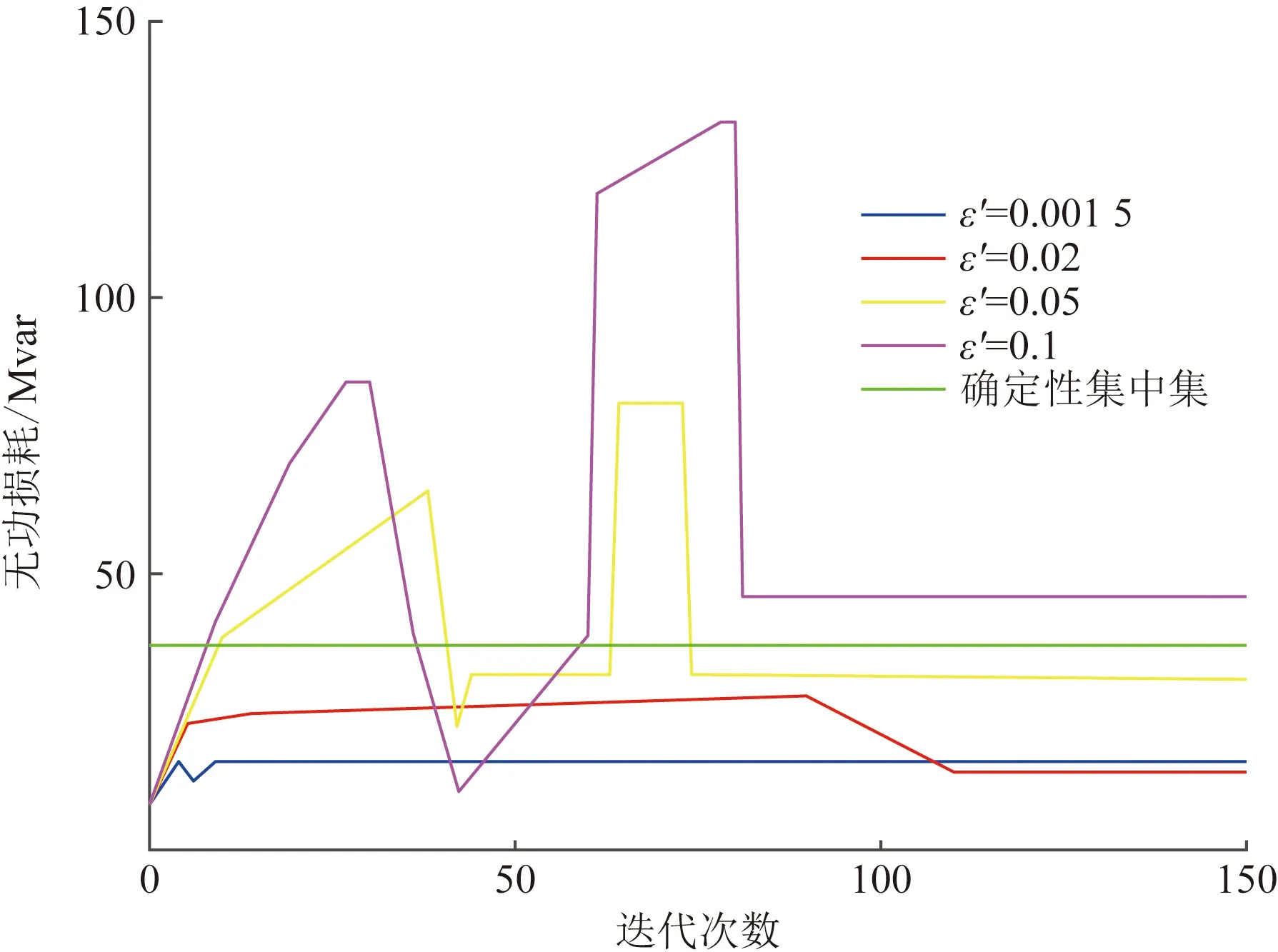
图5 比较ε′不同值下ALADIN算法中分布式光伏逆变器总无功注入量收敛性Fig.5 Convergence performance of total reactive power in ALADIN algorithm under different value of ε′

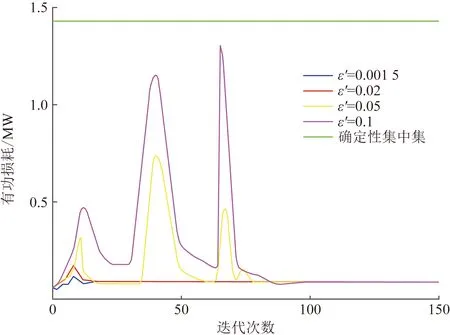
图6 比较ε′不同值下ALADIN算法中分布式光伏逆变器总有功损耗的收敛性Fig.6 Convergence performance of total active power losses in ALADIN algorithm under different value of ε′

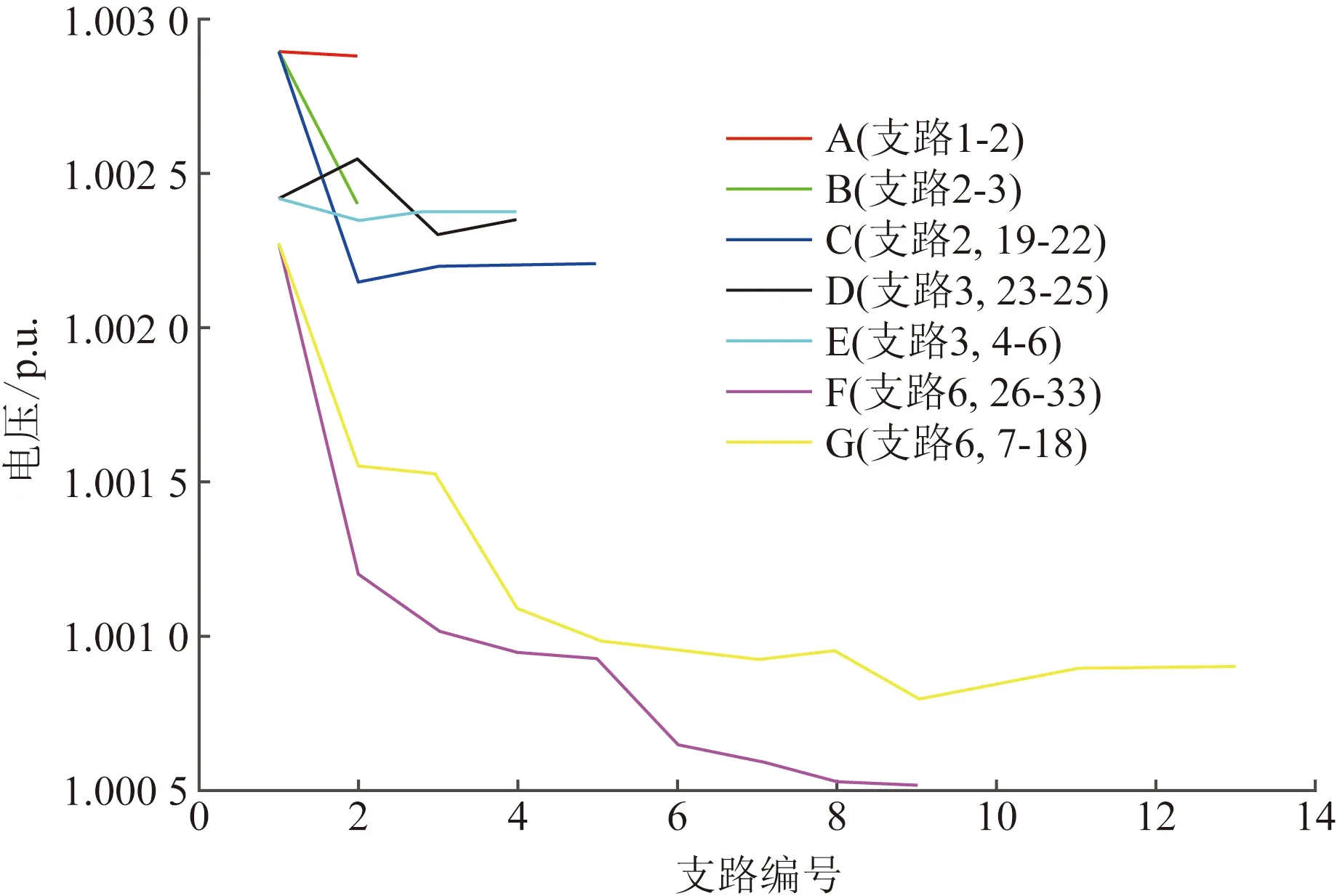
图7 ε′=0.05时分布式优化时配电网不同分支的电压曲线Fig.7 Voltage curves of different branches of distribution network in distributed optimization at ε′=0.05

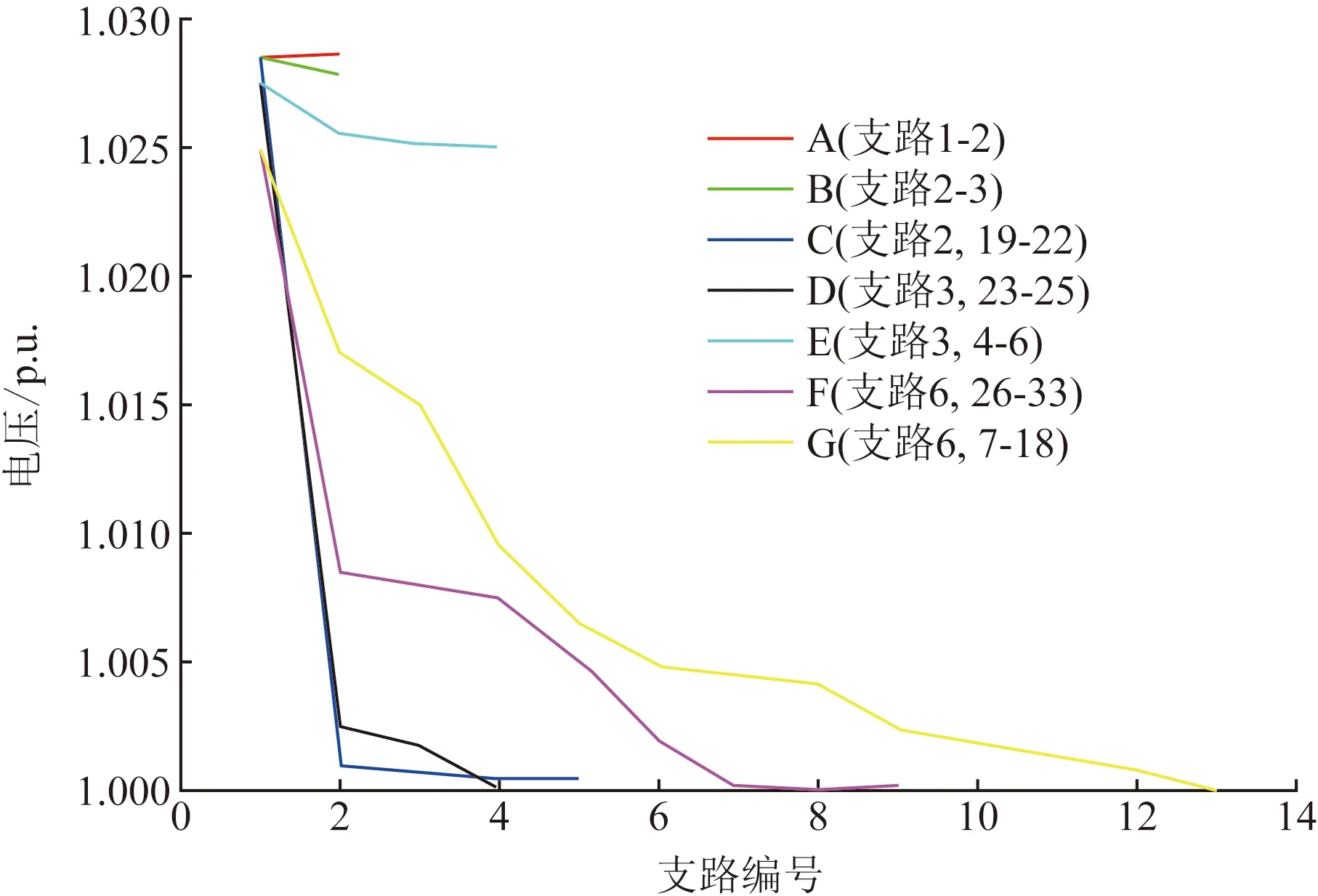
图8 ε′=0.05时集中式优化的配电网不同分支的电压曲线Fig.8 Voltage curves of different branches of distribution network in Centralized Optimization at ε′=0.05

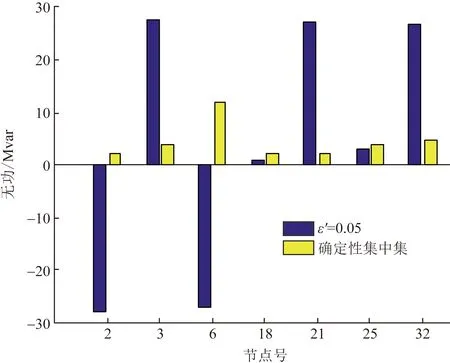
图9 ε′=0.05时集中式优化和分布式优化中每个逆变器注入或吸收的无功功率比较Fig.9 Comparison of reactive power injected or absorbed by each inverter in centralized and distributed optimization at ε′=0.05

4 结论

以实现最小化配电网潮流损耗的目的，提出一种基于配电网的分布式电源逆变器的动态潮流控制策略。考虑到光伏电源出力的不确定性，进一步将所提出的策略拓展为机会约束下的分布式最优潮流。得出如下结论。

(1)算例仿真表明，在确定性场景下，所提策略在有功损耗最小化方面优于现有策略。在考虑不确定场景下，与集中式的确定性优化相比，所提策略减少了几乎所有支路的电压降落，并降低了潮流损耗。

(2)利用机会约束对光伏的不确定性进行建模，做到模型的保守度可调节，并且不会增加计算的复杂度。所提出的方法具有可扩展性，可以适应其他控制策略和分布式电源。