基于自适应层次分析法和变权理论的输电线路铁塔关键指标体系评价方法

魏业文， 姜恒， 杨文超， 聂俊波， 解园琳， 戴北城

(1.三峡大学电气与新能源学院， 宜昌 443002； 2.三峡大学湖北省输电线路工程技术研究中心， 宜昌 443002； 3.三峡大学智慧能源技术湖北省工程研究中心， 宜昌 443002)

输电线路铁塔在野外长期面临风吹日晒等严峻的自然环境，容易发生倾覆和钢筋腐蚀等问题[1-2]。现有的检修工作缺乏针对性，存在着人力、物力资源上的不合理分配问题，检修工作效率低下[3]。随着输电线路在线监测装置和无人机巡检技术的发展[4-5]，对铁塔各项数据的采集越来越便捷，通过对铁塔的历史运行数据进行状态评价来辅助制定检修策略，协助工作人员及时发现铁塔基础设施存在的安全隐患，已成为保证输电线路稳定运行的重要环节。

近年来，中外学者在铁塔状态评价上做了大量研究。文献[6]结合有限元仿真分析了风载荷对输电铁塔的影响，文献[7]采用层次分析法对输电铁塔的不均匀沉降进行了评价，文献[8]运用生命周期评估方法对输电铁塔的不同构件的腐蚀程度与其寿命关系进行了分析。上述研究主要集中在铁塔单一指标或部分结构的分析上，评价体系简单，不能反映铁塔的综合运行状况。文献[9]首次建立了一套完整的输电线路铁塔安全状态评价指标体系，但是其指标体系较为冗杂，所需指标量较多，对巡检工作要求高。文献[10]提出了的输电铁塔的模糊二级评价模型在对权重的设定上主观性较强，未考虑实际工程情况，难以反映铁塔的实际工况。目前电力系统的设备诊断和综合评价方法逐步向智能算法方向发展，研究学者相继将各种智能算法，如贝叶斯网络、随机森林算法、马尔可夫理论、神经网络等运用到电力系统的各种设备诊断和评价中，取得了良好的效果[11-13]。但单一的故障诊断法存在着不足，如贝叶斯网络在数据关键属性缺失时的正确率较低；随机森林算法在处理低维度数据时分类效果不理想；马尔可夫理论不适用于复杂的系统；神经网络依赖大量的样本训练，且计算代价较高。对电力设备的评价诊断目的是为了服务后续的检修工作，但大多数学者注重于理论方法的研究，忽视了评价结果是否可以辅助决策这一关键点。

鉴于此，结合主成分分析法(principal component analysis, PCA)和关联规则建立了铁塔基础关键指标体系及其二级模糊综合评价模型，并考虑到评价指标的均衡性和幅值变化对权重的影响，引入变权公式对初始权重进行了调整，以保证对铁塔异常信息的有效挖掘。

1 铁塔基础安全评价模型

通过关联规则、PCA、自适应层次分析法(self-adaptive analytic hierarchy process, S-AHP)、变权理论和模糊评价法建立了铁塔基础安全评价模型，整体的研究思路如图1所示，具体研究步骤如下。

步骤1通过关联规则对历史运行数据进行量化，然后采用PCA提取关键指标，建立关键指标体系，并通过S-AHP算法确定各指标的初始权重。

步骤2根据建立的关键指标体系及其历史运行数据，结合等级量化标准和三角梯形分布确定各样本二级指标的状态分布矩阵，采用初始权重对二级指标进行模糊评价。

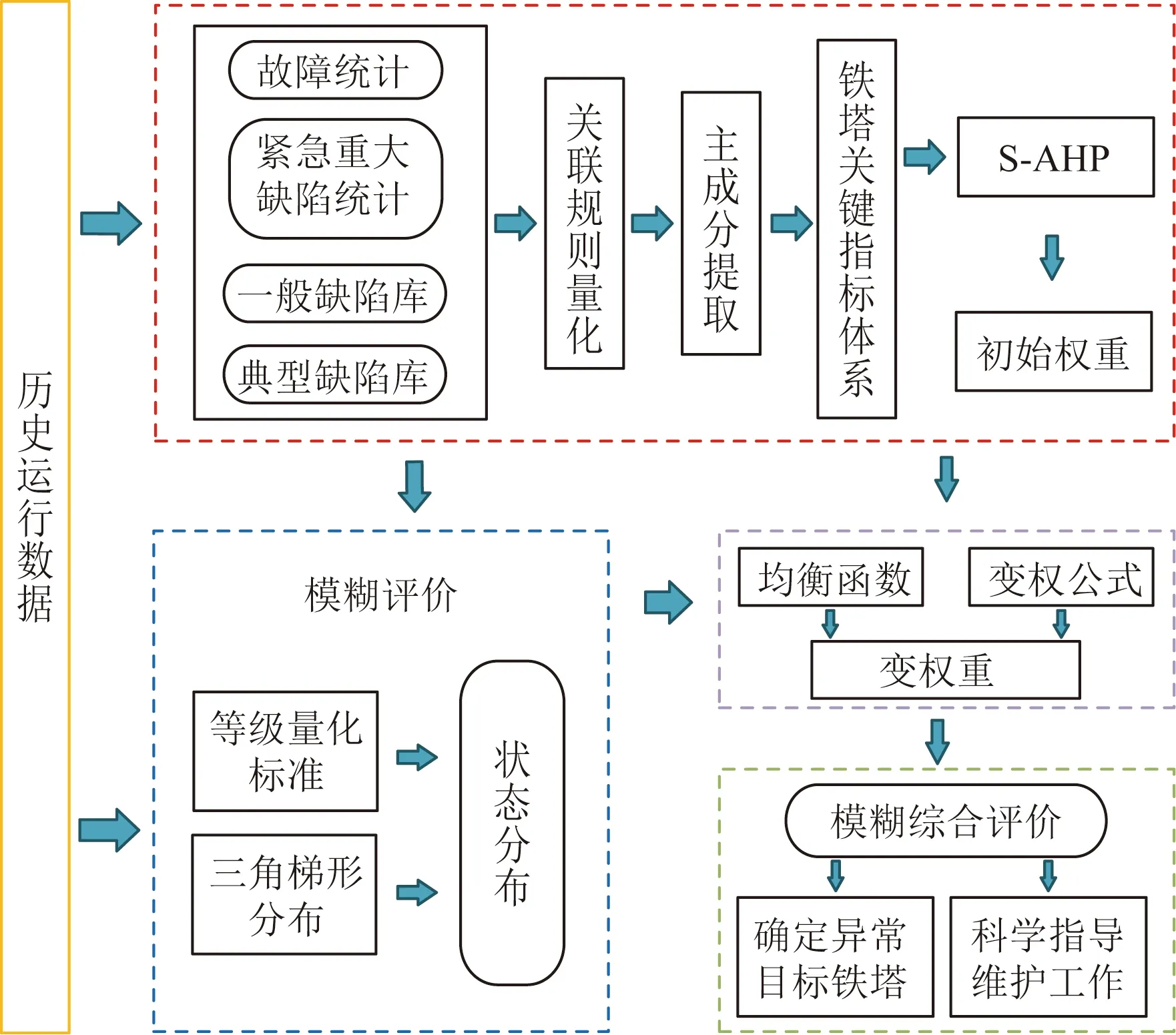
图1 评价模型结构示意图Fig.1 Schematic of evaluation model structure

步骤3引入含有均衡函数的变权公式，根据二级指标的历史数据和其模糊评价结果的幅值变化情况对各初始权重进行调整，得到变权重系数。

步骤4将变权重系数重新输入到模糊综合评价模型中进行运算得到最终的评价结果，根据评价结果确定异常目标铁塔，辅助工作人员制定针对性的检修计划。

2 铁塔基础关键指标体系

目前中国多采用行业标准规定的打分制对所有指标进行评价[14-15]，而铁塔基础评价指标大多由巡检而来，对所有指标进行评价不但会影响巡检效率，而且巡检方式没有统一的规范标准，部分指标对铁塔的缺陷相关性影响并不大，因此有必要选取具有代表性的指标来进行评价。按照关联规则中对支持度和置信度的定义，将铁塔的各个指标量按照历年故障统计、紧急统计、一般缺陷库和典型缺陷库量化为一个4维数组的集合，构建主成分分析矩阵[16]。结合某区域电网输电线路铁塔2012—2019年的历史数据运行记录，以铁塔材质状况为例简述计算步骤如下。

步骤1该线路铁塔2012—2019年发生故障481起，由于铁塔材质状况原因发生的故障有225起，其中因为混凝土碳化引起的故障有22起，则混凝土碳化在故障统计中的置信度x11为10.67%。

同理，按照上述步骤对其他指标的置信度进行计算，得到了材质状况所有指标的置信度，如表1所示。

步骤2提取表1中数据作为材质状况的置信度矩阵X，对该矩阵按列进行离差标准化处理，求取相关系数矩阵R=XXT，对矩阵R进行奇异值分解并计算其特征值λn和特征向量αn。

步骤3计算累计贡献率和综合得分。

(1)

式(1)中：λk为矩阵R的第k个特征值;当累计贡献率αp处于0.85～0.95区间时，则可以用前p个主成分来表征初始指标的信息，1≤p≤n。对p个主成分进行加权，得到综合得分，可表示为

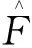
=ωAX

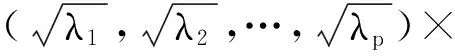
= (λ1α1+λ2α2+…+λpαp)X

(2)

式(2)中：ω为p个主成分对综合得分的权重；A为因子载荷矩阵，由式(2)得到各指标对综合得分的权重H，可表示为

H=(h1,h2,…,hn)

=(λ1α1+λ2α2+…+λpαp)X

(3)

按照上述步骤将表1中数据输入MATLAB中运算，求得特征值并按照大小降序排列：λ1=5.984 1,λ2=1.322 6,λ3=0.685 0,λ4=0.331 2, …,λ10=0。

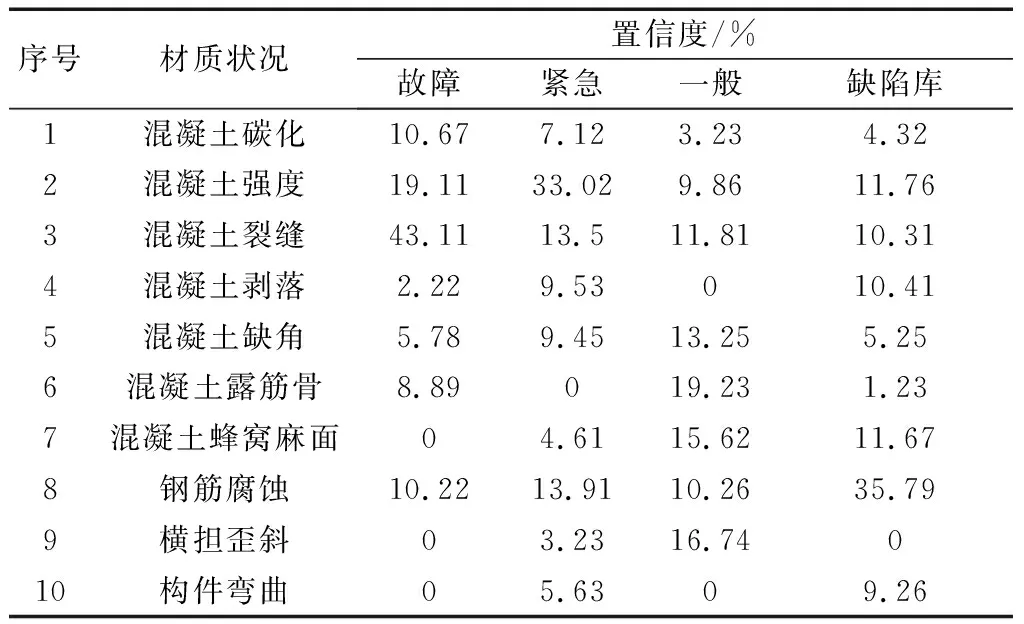
表1 材质状况的置信度Table 1 Confidence matrix of material condition

由式(1)计算得到前4个主成分的贡献率分别为71.899%、15.891%、8.231%、3.979%，前两个主成分的累计贡献率达到了87.790%，属于算法要求的0.85～0.95区间，因此选择前两个特征值和特征向量来计算各指标权重h1,h2, …,hn。将权重归一化后，如图2所示。提取了权重大于0.5的混凝土强度、混凝裂缝和钢筋锈蚀程度指标作为材质状况的关键评价指标。

同理，按照上述方法对整个指标体系进行提取，建立铁塔基础关键指标体系，并对各二级指标的安全等级判定标准进行了量化[17-19]，如表2所示。

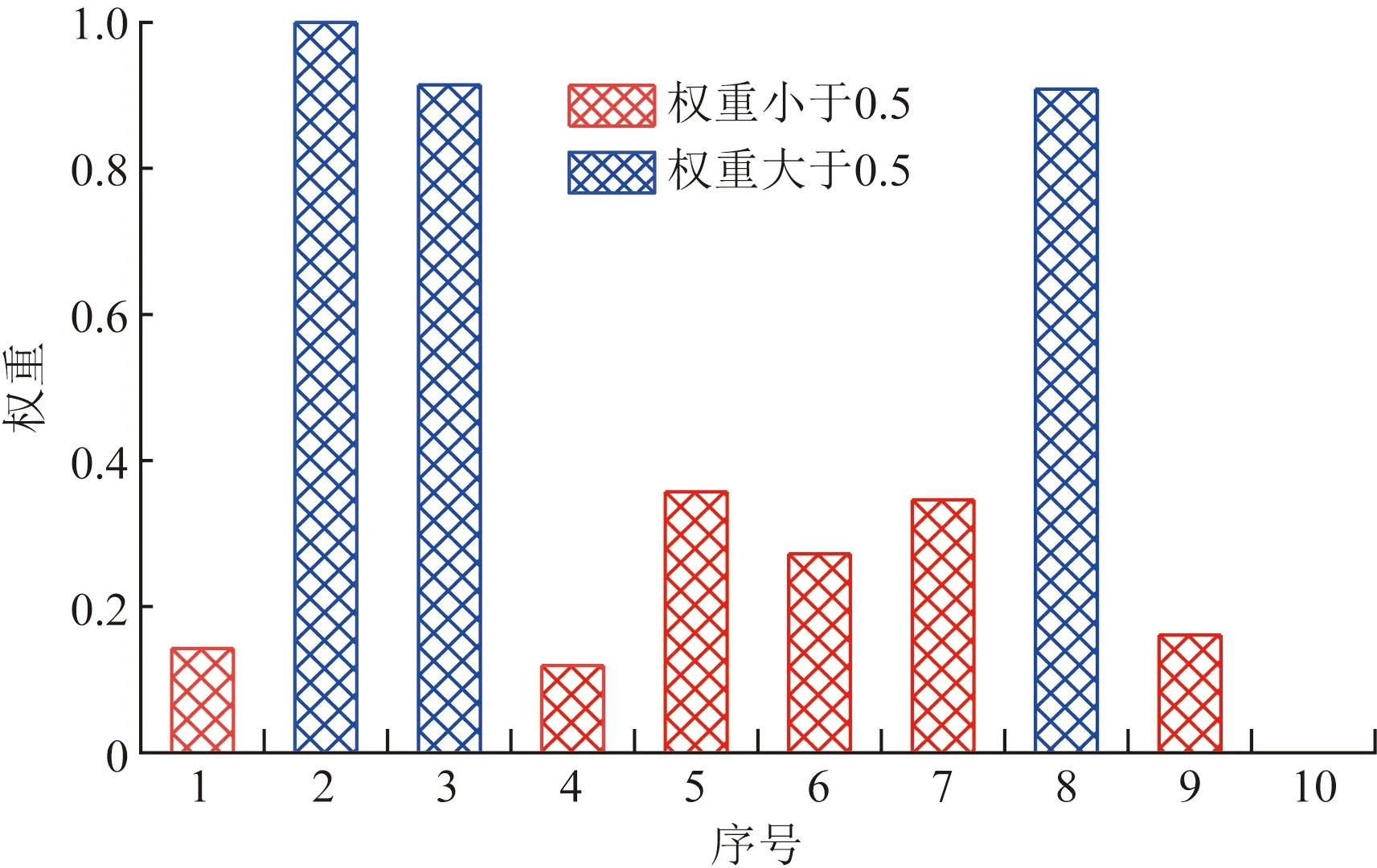
图2 材质状况的各指标权重Fig.2 Weight of each index in material condition

3 铁塔基础评价理论方法

输电线路铁塔基础评价指标状态量多，满足归一化的同时会致使各个因子的权重很小，最终在结果中会淹没大量算子的信息。采用分层评价的方法可以很好解决这个问题，结合输电线路铁塔基础关键评价指标体系，建立了二级评价因素集，如图3所示。

根据模糊数学理论及上述因素集，建立输电线路铁塔基础的模糊二级综合评价模型。对于二级指标，其模糊评价计算模型为

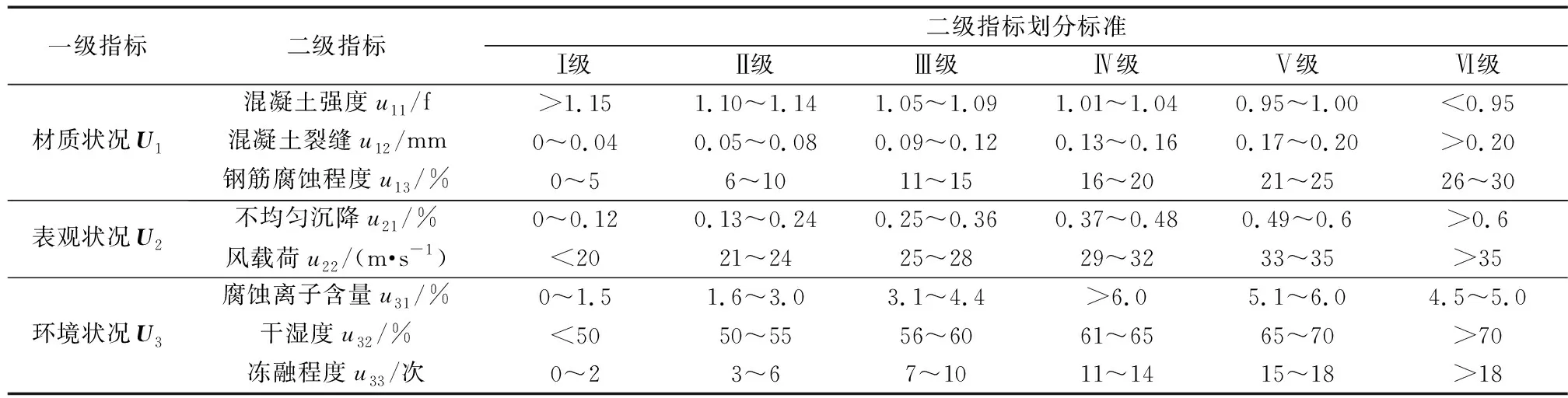
表2 铁塔基础关键指标体系及其安全等级判定标准Table 2 The key index system of transmission tower foundation and its safety grade judging standard

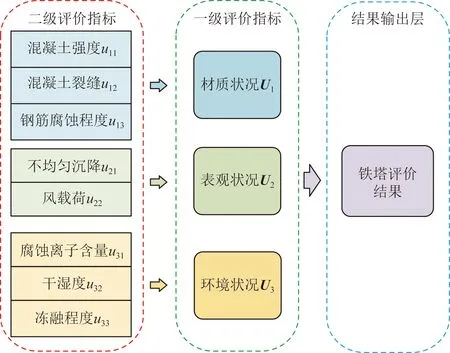
图3 铁塔基础评价因素集Fig.3 Evaluation index set for transmission tower foundations

Bi=Airi

(4)

式(4)中：Ai为3个一级指标各自所对应的二级指标的权重行向量；ri为3个一级评价指标Ui(i=1,2,3)分别对应的二级指标uij所对应的隶属度向量所构成的评判矩阵。r1为一级评价指标U1所包含的3个二级指标u1j(j=1, 2, 3)的隶属度向量组成的3×6阶的矩阵，其中二级评价指标u11的隶属度向量为(u111u112u113u114u115u116)，其中u111、u112、u113、u114、u115、u116分别为u11对应表2中6个安全等级隶属度的值；Bi为3个一级评价指标的评判结果的行向量。

对于铁塔基础总体，其运行状态评价采用的一级模糊综合评判计算模型为

B0=A0[B1,B2,…,Bi]Τ

(5)

式(5)中：A0为一级指标各自所对应的权重行向量；B0为铁塔基础设施总体的评判结果行向量。

3.1 评语集

表2中确定的6个安全等级评语较为模糊，实用性不强。为满足实际工程应用的需求，需对评语集进行量化，采用百分制对评语集进行量化，各个安全等级所对应的量化值定义为

(6)

式(6)中：v为各个二级指标的量化值。

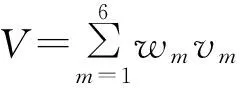
(7)

式(7)中：V为综合得分；wm为模糊评价结果行向量的第m列值；vm为各等级的量化值，取式(6)中各等级标准的中间值，如当m=1时，v1=95。

3.2 S-AHP和变权理论

层次分析法(analytic hierarchy process, AHP)常被用在模糊评价中确定权重向量，传统AHP的流程如图4(a)所示。

在传统AHP算法中，必须要通过一致性检验，而在实际工程应用中，一旦不能通过一致性检验，需要对判断矩阵进行一次甚至是多次的调整，这样的做法带有盲从性，会影响最终权重的可靠程度。采用了S-AHP算法，其流程如图4(b)所示。该算法综合考虑了本行业专家对各指标间相互重要程度的判断信息，将初始判断矩阵A进行调整，得到初始判断矩阵的拟优一致阵A*。调整后的矩阵能够最大程度上保留原始矩阵的信息，同时能够自动满足一次性检验，优化主观判断上的不一致性，避免了因为多次调整判断矩阵引起的主观盲从性。

针对所涉及的评价指标，建立了9标度的判断矩阵取值表，如表3所示。根据传统AHP建立铁塔基础一级指标的判断矩阵，通过S-AHP算法，将判断矩阵进行改造，得到一级指标的权重，如表4所示。同理，得到各二级指标的权重，如表5所示。

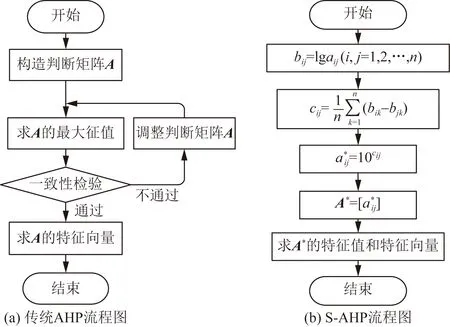
n为判断矩阵的阶数，aij为判断矩阵A的第i行第j列元素；A*为判断矩阵A对应的拟优一致矩阵；为中间计算变量图4 AHP流程图Fig.4 AHP flow chart

表3 判断矩阵取值Table 3 Value of judgment matrix

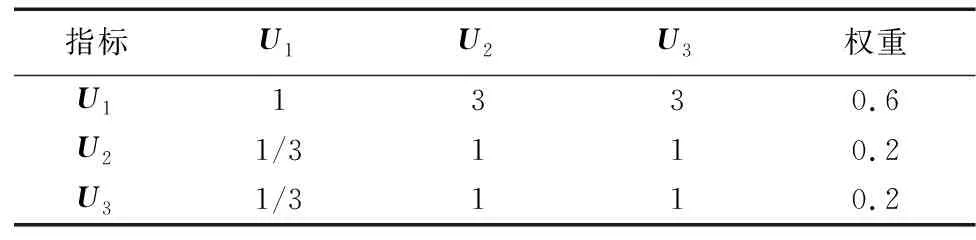
表4 一级指标权重Table 4 Weights of first-level indices

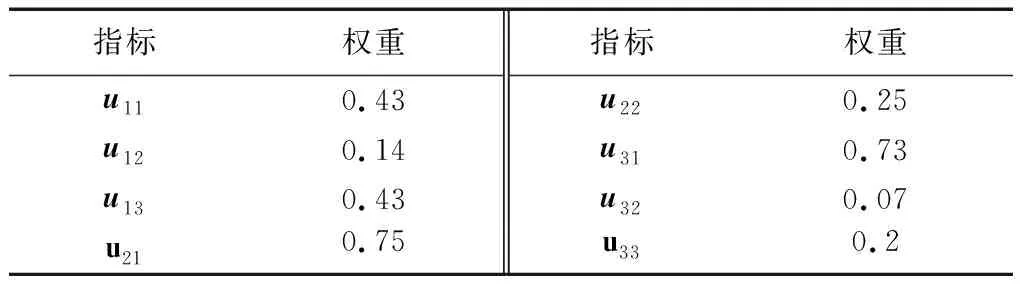
表5 二级指标权重Table 5 Weights of second-level indices

S-AHP算法虽然在一定程度上解决了构建指标间判断矩阵时的主观盲从性问题，但是权重较低的指标在严重偏离正常值时不能通过模糊评价突显出来，无法反映工程实际状况。对此，考虑到各二级指标的历史数据和其模糊评价结果的幅值变化情况，引入变权公式，可表示为

(8)

式(8)中：w′为某项指标变权后的权重系数；w为某指标变权前的权重系数；vj为该指标第j个样本的量化值；m为样本个数；wi和vij分别为第i个指标的权重系数和其对应的样本量化值，i=1, 2, …,n，其中n为各级指标中分别对应的指标个数，当对材质状况所对应的3个二级指标进行变权时，n=3；当对3个一级指标进行变权时，n=3；α为由状态量的值影响的均衡系数，为突显综合结果中状态量的缺陷[20]，α取2.5。

3.3 隶属度的确定

采用经过改进的三角形梯形隶属度分布模型，如图5所示。改进的三角梯形分布的隶属度函数表达式为

(9)

式(9)中：f(v6)、f(vi)、f(v1)为二级评价指标对6个状态级别的隶属度函数,i=5, 4, 3, 2；v为二级指标的量化值，模糊分界线需具备一般性，即取式(6)的中值:v6=15,v5=45,v4=65,v3=80,v2=85,v1=95。

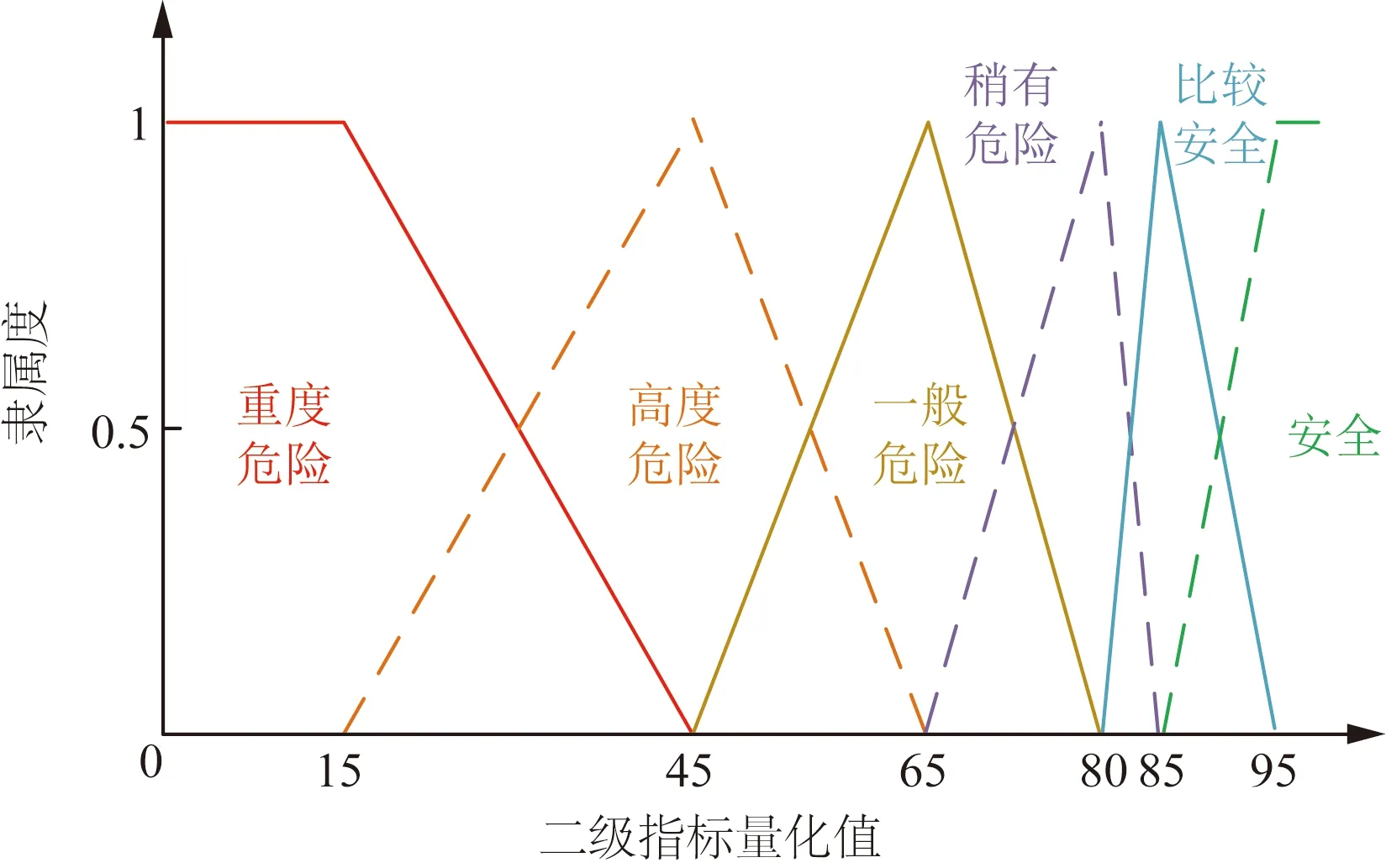
图5 改进的三角梯形分布Fig.5 Improved triangular and trapezoidal distribution

4 算例分析

输电线路铁塔分为耐张塔和直线塔。较直线塔，耐张塔除了要承受输电线路导线和线路金具的重力荷载，还要承受外界条件引起的附加荷载、沿线路方向的张力和因事故断开而产生的纵向不平衡张力等。因此选取耐张塔进行算例分析会更具有代表性，同时也能有效避免数据的冗余性，降低运算次数。以耐张塔为分析对象，首先按照传统的累计扣分制对比了不同指标体系下的评价结果，然后在关键指标体系的基础上对比了常权模型和所提变权模型下的模糊评价结果，以验证模型的可靠性。

4.1 关键评价指标体系的可靠性验证

按照传统的累计扣分制[14-15]，需对铁塔的各一级指标进行加权扣分。考虑受到季节气候的影响，结合某电网公司一座耐张塔2019年12个月的历史运行数据，进行了不同指标体系下的评价结果分析。表6为该铁塔1月份的扣分细则，其加权得分评价如表7所示。

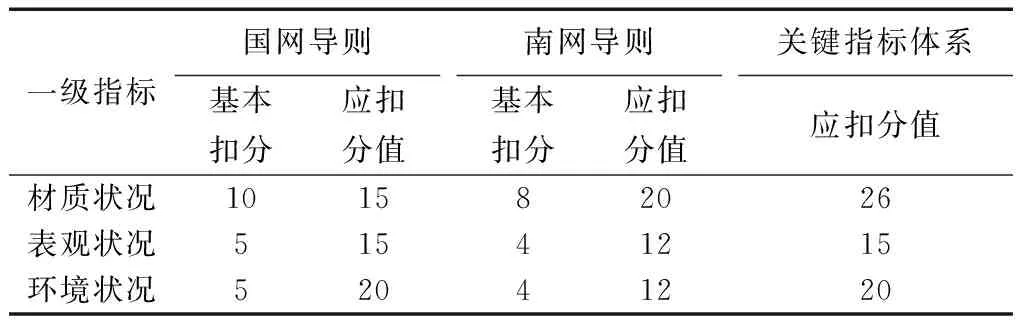
表6 1月份扣分细则 Table 6 Scores deduction details for January

同理，按照上述步骤对该铁塔其他月份的状态进行了评价，如图6所示。根据表7和图6中的评价结果可知，铁塔的关键指标体系与两大导则体系的评价结果虽然稍有差异，但是基本符合铁塔的实际运行状况。这说明铁塔的关键指标体系综合了行业的技术规范要求，可以反映出铁塔的整体运行状况。同时它精简了评价指标的数量，在实际运维中能够降低工作量，提升运维效率。

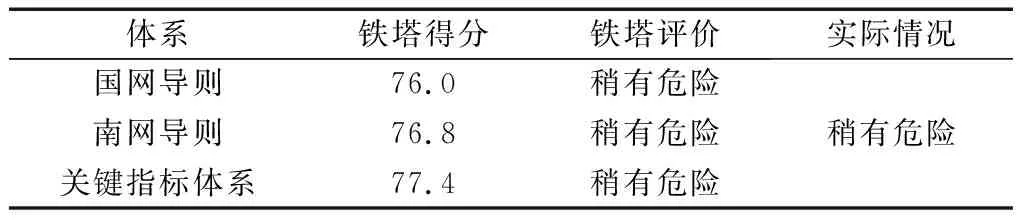
表7 1月份的加权得分评价Table 7 Evaluation results for January

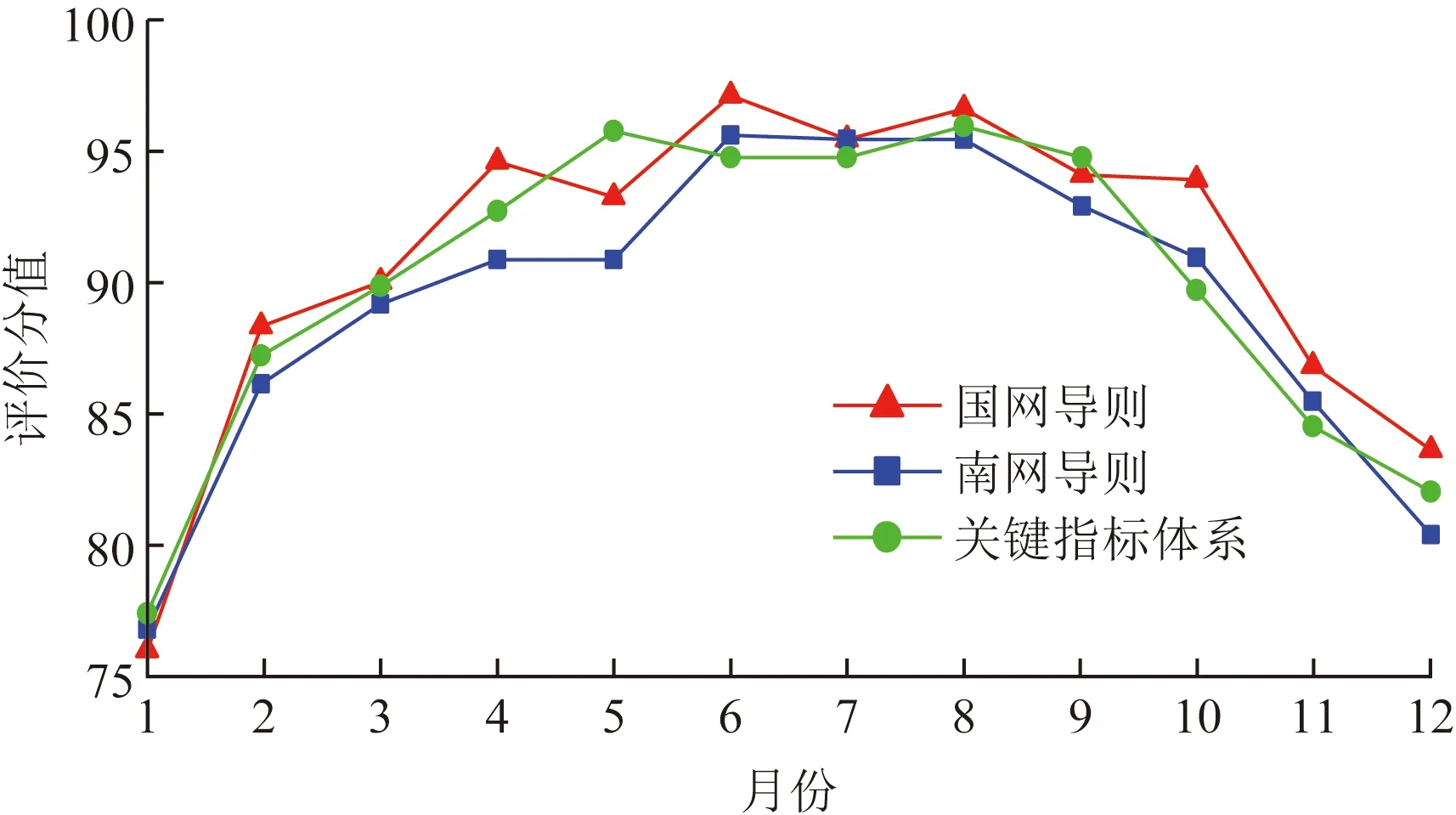
图6 各指标体系下的结果对比Fig.6 Comparison of results under each index system

4.2 变权前后模糊评价结果分析

结合某网公司2019年6月份50座耐张塔的历史运行数据进行分析。按照表2中标准与式(7)，将1号塔的实测数据进行量化，如表8所示。同理，按照上述步骤对其他铁塔的实测值进行了量化，如图7所示。

将初始数据输入到常权评估模型，得到各耐张铁塔的一级评判向量和最终的耐张铁塔基础评判向量，采用式(7)对评判结果进行量化，根据量化值按照变权式(8)对权重系数进行调整，调整后的权重系数如表9所示。

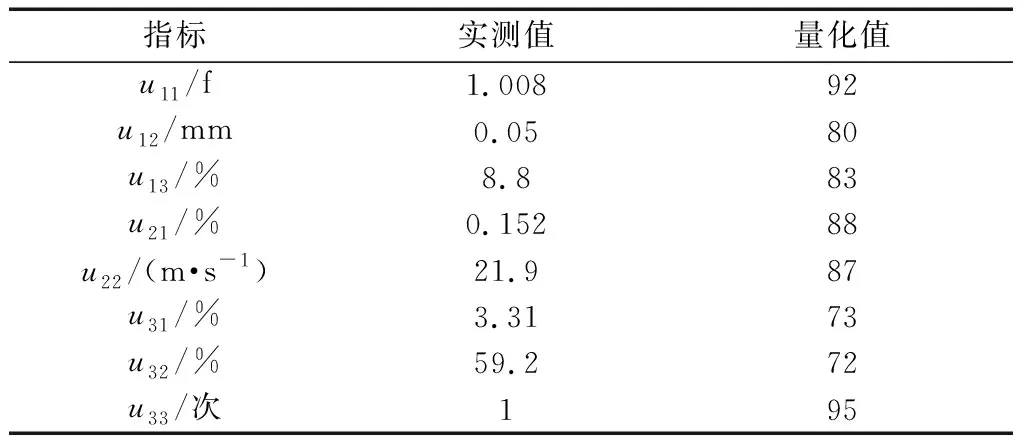
表8 一号塔的实测值与量化值Table 8 Measured and quantified scores of the No.1 tower

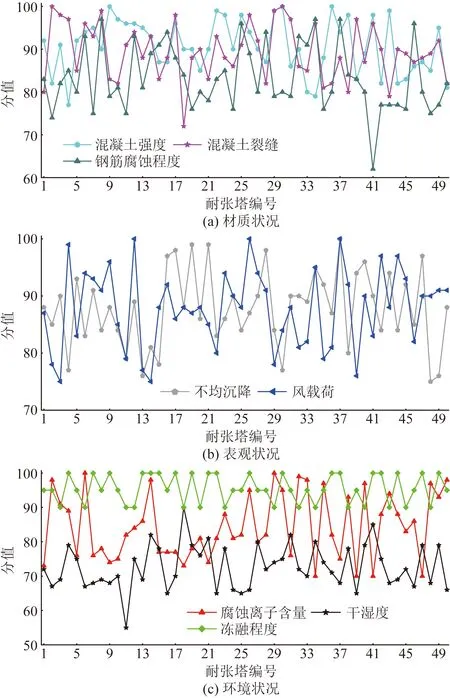
图7 耐张塔量化值数据曲线Fig.7 Quantification data curve of strain towers

表9 各指标变权后的权重系数Table 9 Weight coefficient of indexes after weight change

将表9中的权重重新输入评价模型中，得到变权后各铁塔的一级评价及综合评价结果，图8为各铁塔一级指标变权前后的评价结果对比。该段线路铁塔变权后材质状况得分下降了1.66%，环境状况评分下降3.66%，这与表9中锈蚀程度u13和干湿度u32权重上升相吻合。

图9为变权前后的综合评价结果对比，变权前后平均得分为：85.2分和83.6分，变权前后该线路段铁塔基础总体结果差异不大，均为比较安全的状态，这说明变权处理能够保证最终评价结果的准确

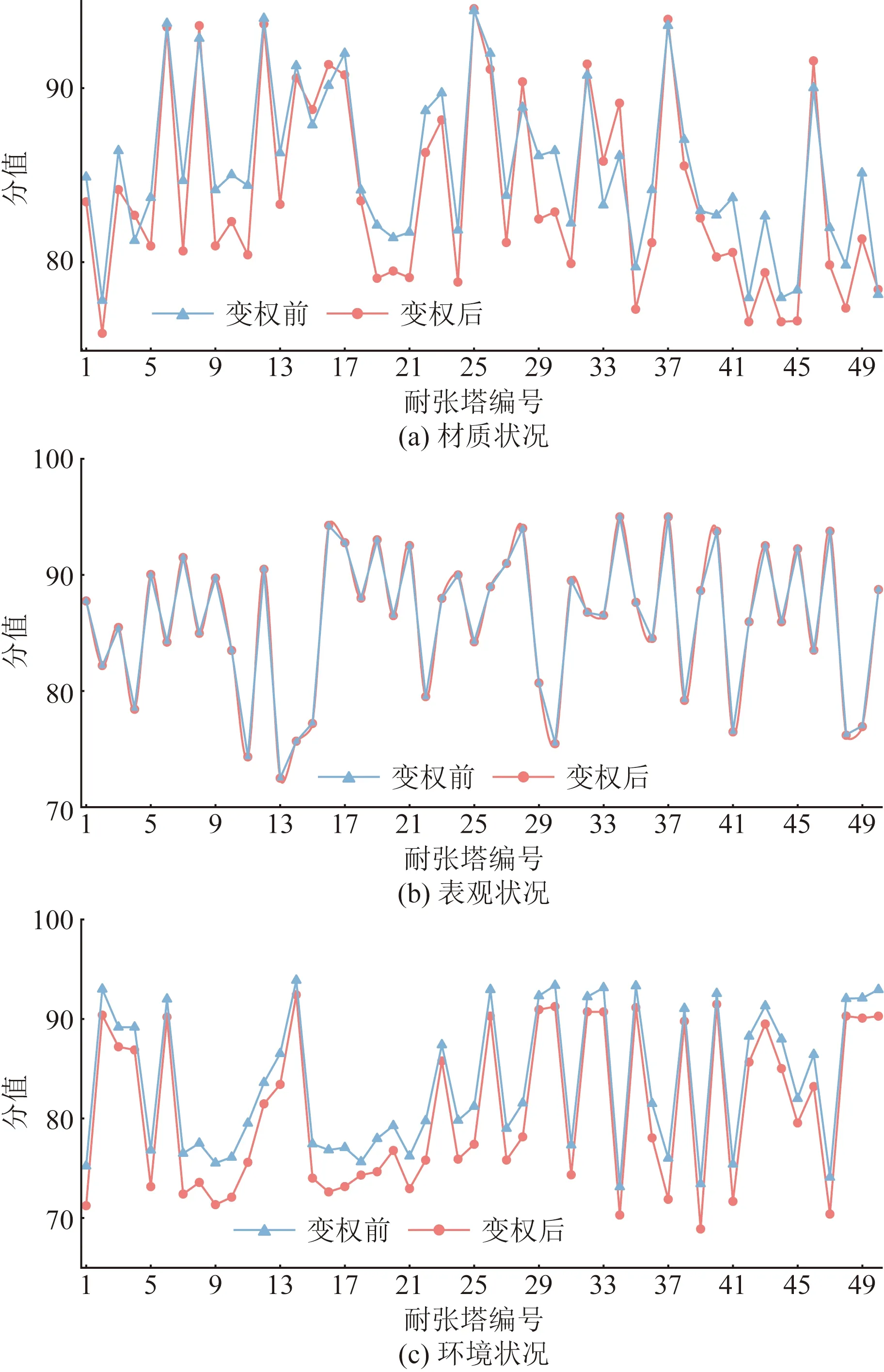
图8 一级指标变权前后评价结果对比Fig.8 Comparison of evaluation results of first-level indices

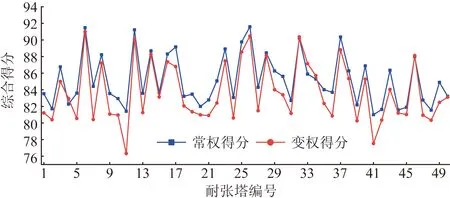
图9 变权前后综合评价结果对比Fig.9 Contrast of of comprehensive evaluation results before and after weight change

性。变权后该段铁塔总体评分下降1.92%，这是由于部分指标偏低所致，可以确定是该段线路铁塔的锈蚀程度和干湿度指标偏低导致的。

图9中11号耐张塔和41号耐张塔的评价结果在常权与变权评价下的结果差异较大，常权下两座铁塔的等级状态是比较安全，变权结果下为稍有危险状态。结合图7中两座耐张塔的数值曲线可以确定11号铁塔的腐蚀程度和41号铁塔的干湿度已经严重偏离了正常值，较变权前，变权后的评价结果将这一问题突显了出来，这说明变权处理能够解决常权系数下铁塔某项指标出现异常时对模糊评价结果无影响的问题。

综合上述对评价结果的分析，检修人员应密切注意11号铁塔和41号铁塔的状态发展，尽快安排检修。同时应关注该段线路铁塔的干湿度和锈蚀程度指标，加强防腐蚀工作。

5 结论

建立了一套完整的输电线路铁塔基础设施评价体系和评价方法，具有代表性强，可靠性高的特点，为铁塔评价研究和线路检修工作提供了新的思路。得出如下主要结论。

(1)通过主成分分析法和关联规则建立了铁塔基础评价体系，相比于现有的参数体系更为精简，代表性更强，在保障评价结果准确性的前提下降低了参数体系的复杂性。

(2)建立了输电铁塔基础设施二级模糊评价模型，在综合评价结果中能保留全部算子的信息，评价结果全面可靠。

(3)采用S-AHP算法确定初始权重，避免了多次调整判断矩阵引起的主观盲从性问题，引入含均衡系数的变权公式，对初始权重系数进行了合理的调整，使得评价结果能够贴合工程实际状况。