考虑源荷不确定性及配电网接纳裕度的弹性调度策略

王凌云， 应利*， 阮胜冬， 史伟明

(1. 三峡大学电气与新能源学院， 宜昌 443002； 2. 国网浙江衢州供电公司， 衢州 324000)

目前，配电网面临着各种不确定扰动的冲击，其中一类是渐进式加剧的小扰动事件，包括风、光和电动汽车(electric vehicles, EV)等大规模发展和并网，严重威胁着电网的经济安全运行[1]。因此，研究在不同扰动下如何提升配电网的弹性成为电网调度的主要问题。

弹性电网建设工作加快开展，中外专家在此基础上建立了相关理论体系，研究工作已经初具规模[2-3]。文献[4-5]提出了弹性电网包括感知力、适应力、抵抗力、恢复力4个方面，并对未来发展方向进行介绍；文献[6]研究电网弹性重构问题，提出了考虑接入配电网功率灵活性的弹性调度策略，但区间优化处理不确定性存在区间划分不够准确的缺点；文献[7]提出一种具有分布式电源的配电系统的模糊多智能体自愈方案，通过弹性调控克服了配电网电压严重超标的问题。

配电网对EV的接纳能力是有限的，超过电网可接纳最大裕度会影响电网的安全经济运行，因此需要对此进行定量评估。文献[8]提出了考虑风电和EV弹性裕度的评估模型，并采用三点估计法处理不确定性，但以安全距离作为评估指标仍不足以提供弹性调度决策依据；文献[9]对电动汽车充电站进行规划研究，并采用量子粒子群算法进行求解。文献[10]以功率损耗和电网主负荷系数等指标表征EV接入电网带来的影响，促进EV有序充电。

此外，实现源荷两侧的良性互动，还需充分挖掘用户侧的调节作用。文献[11]为促进风电消纳，对需求侧资源进行了分类研究，实现电网经济运行；文献[12]研究价格型与激励型需求侧响应对系统运行成本的影响，并采用改进粒子群算法对模型求解，但算法极易陷入局部最优。文献[13]分析了用户需求弹性变化的不确定性，建立多目标鲁棒优化模型，并提出系统弹性运行规划方案。

针对以上问题，提出综合考虑风光出力和EV功率不确定性及配电网接纳裕度的弹性调度策略，构建需求侧和电网运行两阶段模型。以配电网对EV接纳能力最优和系统运行成本最小为目标，采用基于反向学习的种群初始化法和自适应系数的改进人工蜂群算法(artificial bee colony algorithm，ABC)进行求解，与粒子群和常规人工蜂群算法进行对比。通过IEEE 33节点系统验证所提策略的有效性。

1 配电网弹性接纳裕度

1.1 接纳裕度区域划分

配电网弹性是指配电网应对不确定性变化或扰动，能够灵活适应条件变化的能力。通过研究配电网对EV的接纳能力，实现配电网弹性调度。接纳能力主要指在满足节点电压、线路载流等多种安全运行条件下，EV接入对配电网安全稳定运行的影响和配电网中允许接入EV的最大容量。根据电网接纳的安全性和经济性，按图1所示的接纳裕度区域划分方式，将其分为：①优质区：具有灵活的调节裕度，同时满足安全性和经济性，配网中的节点仍能继续接入EV；②警戒区：接纳裕度处于警戒状态，只能满足安全性，需要进行提升优化才能满足经济

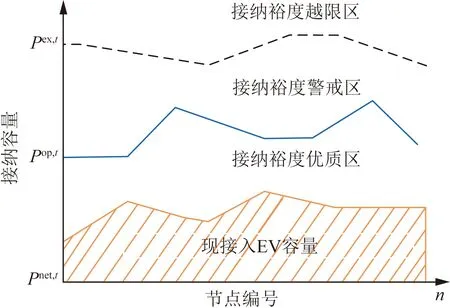
为t时刻节点i极限接纳容量；为t时刻节点i最优接纳容量；为t时刻节点i入网功率；n为系统中节点总数图1 接纳裕度区域划分Fig.1 Division of acceptance margin region

性要求；③越界区：接纳裕度严重不足，不能安全经济运行，不能再继续接入EV。

1.2 接纳裕度评估指标

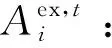
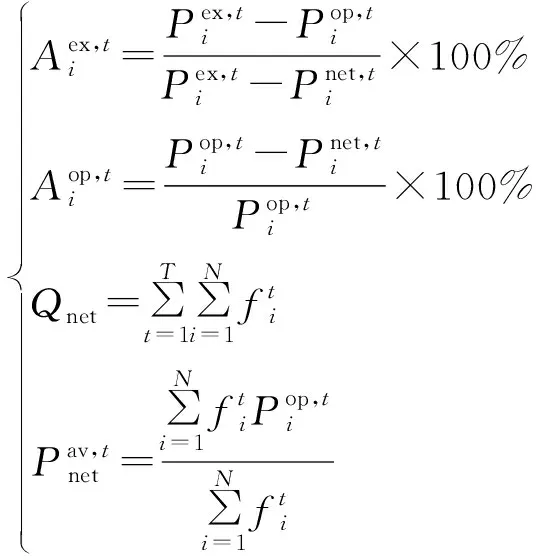
(1)

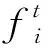
2 风、光和EV不确定性模型

2.1 风、光出力不确定性模型

现有文献表明，风速满足Weibull分布[14]，其概率密度函数可表示为

(2)

风力发电机组与风速的关系式为

(3)

式中：k和c分别为形状参数和比例参数；v为风速；PWT为t时刻风力发电机组的输出功率；Pc为额定输出功率；Vin、Vout和Vc分别为风力发电机的切入风速、切出风速和额定风速。

Beta分布用于描述光照强度的概率模型，可表示为

(4)

光伏机组输出功率与光照强度成正比例关系为

(5)

式中：rt为t时刻的光照强度；rmax为最大光照强度；α和β为Beta分布的形状参数；Ppvt为光伏机组输出功率；Z为光伏电池的组件数；Sz和ηz分别为第z个组件面积和光电转化效率；S和η分别为光伏电池阵列的铺设面积和光电转换效率。

2.2 EV不确定性模型

电池在充电过程中能够随时获取荷电状态，开始充电时刻用正态分布描述，概率密度函数为

(6)

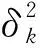
EV充电瞬时SOCc(t)随充电时间呈指数分布，可表示为

SOCc(t)=SOCmax(1-e-γt/tmax)+SOC0

(7)

式中：SOCc为电动汽车充电瞬时荷电状态；SOCmax为电动汽车充电最大荷电状态；SOC0为初始荷电状态；SOCmax取0.9；t为EV充电时间；tmax为电池的最大充电时间；γ由完全充电的电池计算得出，表示该电池在最大充电时间的1/3期间吸收了90%的充电状态。

3 拉丁超立方场景优化

风光出力和EV功率预测信息对制定合理的调度计划有重要意义。风光和EV服从概率分布，称为“场景”。基于历史数据确定风光出力和EV功率预测的概率分布函数，运用拉丁超立方抽样(Latin hypercube sampling, LHS)产生大量随机场景[15]，确保所有抽样点均被抽样，再采用后向场景削减技术对一些相似和极端的场景进行削减，得到典型场景和概率。其具体步骤如下。

步骤1假设有一个K=[1,2,…,M]维的随机变量X，风光出力和EV的概率分布函数为Yi=Fi(i=1,2,…,K)，其中Yi为风光出力和EV的概率分布函数。

步骤2在每个元素中抽取N次样本，得到第k个元素的第j次抽样xjk(j=1,2,…,N)。

步骤3对抽取的样本进行随机组合，生成所需场景值，得到计及风光和EV功率不确定性的采样矩阵即N×M维矩阵P=[νi,rj,Ep]。

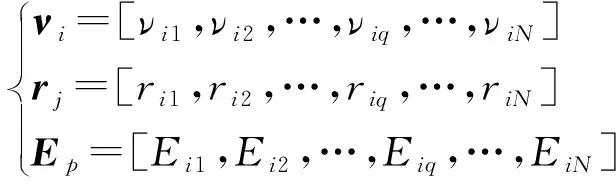
(8)

式(8)中：νi、rj、Ep分别为风速、光照强度、EV功率的第l次抽样数据。

步骤4设原有场景集为B，迭代次数需要削减的场景集J为空集。计算任意2个场景的场景距离形成场景距离矩阵D[ω(Si),ω(Sj)]=‖ω(Si)-ω(Sj)‖2，其中，ω(Si)为不确定性场景，Si和Sj为场景编号，‖·‖为向量空间欧氏距离运算符。

步骤5设场景Si发生的概率为pi，求得与场景Si最近场景Sk的最小距离概率PDi，PDi=pimin{D[ω(Si),ω(Sk)]}。

步骤6在当前所有场景集合C中找最小的pDb=minPDi，其中pDb为搜索所有场景集合C中Si最近场景Sk的最小距离概率。

步骤7更新场景集合B和计划削减场景的集合J，并更新场景概率pi=pi+pDb。

采用拉丁超立方抽样生成2 000个日时间尺度下风、光和EV功率场景，再通过后向场景削减技术筛选得到5个典型场景，各场景下功率情况如图2所示。

4 EV需求侧响应模型

现阶段，需求侧响应主要分为激励型需求响应和电价型需求响应，后者是用户根据市场电价动态改变固有用电模式以提高经济性的方式。随着EV广泛接入电网，EV用户用电具有一定的弹性和波动性，建立考虑需求弹性的EV充电站负荷需求侧响应模型，引起用户用电量的变化，引导用户转移充电时段和调整充电需求，从而提高配电网对EV的接纳水平，进一步增强配电网应对不确定性扰动

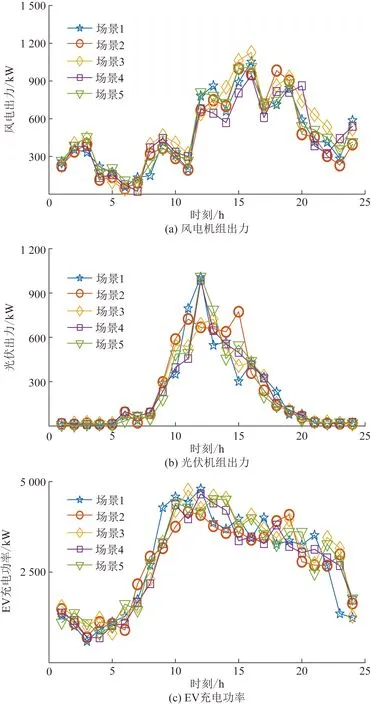
图2 典型场景下风电、光伏出力和EV功率情况Fig.2 Wind power, photovoltaic output and electric vehicle power in typical scenarios

的能力[16]。设定峰平谷三时段电价进行需求侧响应分析，弹性系数h和需求弹性矩阵H可分别表示为

(9)

(10)

式中：q、p为某时刻电量和电价；Δq、Δp为下一时刻电量和电价改变量；H矩阵为需求弹性矩阵，dqf、dqp、dqg矩阵为不同时段峰平谷电量需求的变化矩阵；dpf、dpp、dpg矩阵为不同时段峰平谷电价的变化矩阵；hff、hpp和hgg分别为不同时段的电量电价自弹性系数；hfp、hfg、hpf、hpg、hgf、hgp分别为不同时段的互弹性系数。

利用式(10)求出电价的变化量，进而求出峰平谷时段的电价情况。

5 配电网弹性优化调度

以接入配电网的风光和EV为研究对象，考虑EV需求侧响应进行调度，建立配电网接纳裕度最优、系统运行成本最小的两阶段优化调度模型。

5.1 计及EV接纳的需求侧响应模型

5.1.1 目标函数

配电网接纳EV充电负荷的能力F1最大。

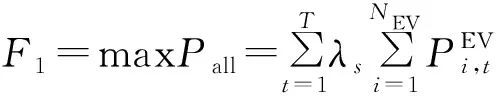
(11)

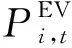
5.1.2 约束条件

(1)EV充电约束。

(12)

(2)需求响应约束。

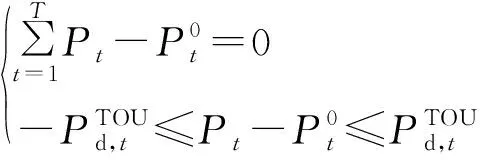
(13)

(3)电价约束。原则上，电价满足谷时电价低于平时电价，平时电价低于峰时电价，谷时电价低于固定电价，峰时电价高于固定电价。

5.2 考虑系统运行成本的经济调度模型

5.2.1 目标函数

系统运行成本F2最小，包括向上级电网购电成本fgrid、柴油机组燃料成本fDE、机组维护成本fop和系统网损成本floss。

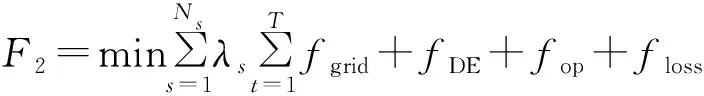
(14)

式(14)中：Ns为总场景数；T为调度周期，为24 h。

(1)向上级电网购电成本：配电网在柴油、风光机组出力后，其余所需功率向上级电网购电。

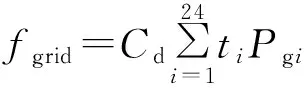
(15)

式(15)中：Cd为单位功率的购电费用，Pgi为向上级电网所购电量。

(2)柴油机燃料成本：

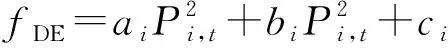
(16)

式(16)中：Pi,t为柴油机组i在t时输出功率；ai、bi、ci为机组i的燃料成本系数。

(3)维护成本：

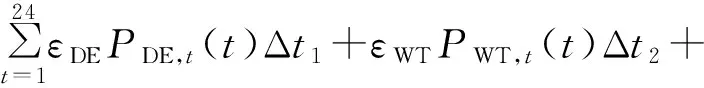
εPVPPV,t(t)Δt3

(17)

式(17)中：εDE、εWT、εPV为各机组的维护成本系数；PDE,t(t)、PWT,t(t)、PPV,t(t)为各机组出力；Δt1、Δt2、Δt3为时间尺度。

(4)系统网络损耗成本：考虑各时段EV接入配电网充电产生的网络损耗，其计算公式为

(18)

式(18)中：ft,loss为t时刻的网络损耗；b为支路数；Rj为第j条支路的电阻；Ptj、Qtj、Utj分别为t时刻支路j始端的有功功率、无功功率、电压。

5.2.2 约束条件

(1)系统运行约束：

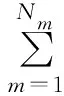
PL(t)+PEV+Ploss(t)

(19)

式(19)中：Nm、Nw和Np分别为柴油机、风电机组和光伏机组的数量；PEV为EV充电功率；PL(t)为基础负荷；Ploss(t)为网损量。

(2)配电网潮流方程约束：

(20)

式(20)中：Uj,t、Ui,t分别为节点j和节点i在t时刻的电压幅值；Pi,t、Qi,t分别为t时刻节点i的有功、无功功率；Gij和Bij分别为支路i、j的电导、电纳；θij为节点i、j的相位差。

(3)DE启停时间约束：

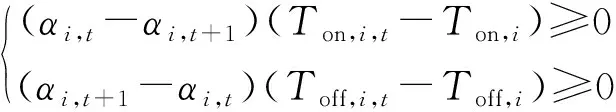
(21)

式(21)中：αi,t为t时刻第i台机组启停的0-1状态变量；Ton,i,t、Toff,i,t分别为t时刻第i台机组连续开机、关机时间；Ton,i、Toff,i分别为最小开机和停机时间。

(4)网络节点电压约束：

Uj,min≤Uj(t)≤Uj,max

(22)

式(22)中：Uj为节点j的电压幅值；Uj,min和Uj,max分别为节点j允许运行的电压幅值上下限。

5.3 改进人工蜂群算法求解

建立的需求侧和系统运行两阶段调度模型为最优化求解问题，且求解过程复杂，因此考虑第一阶段采用运用Yalmip建模语言联合CPLEX求解器进行求解，第二阶段采用智能算法求解。人工蜂群算法作为一种群体智能算法，在水电调度、电网重构等问题中得以应用，蜂群包括采蜜蜂、观察蜂和侦察蜂。该算法鲁棒性强，但存在搜索速率慢和易陷入局部最优等问题[17-18]。

因此，通过引入反向学习的种群初始化法和自适应系数ω′对算法进行改进。通过采用反向学习的种群初始化方法，可以在搜索空间初始迭代时产生可能更靠近最优蜜源的相反解，从而有效减少迭代次数；ω′可在搜索过程中动态调整蜂群采蜜情况。采用改进人工蜂群算法对需求侧和系统运行侧两阶段调度。求解流程如图3所示。

步骤1设解空间是D维，确定采蜜蜂、观察蜂和蜜源的个数为SN。在初始迭代时生成一组初始解Xi={xi,1,xi,2,…,xi,D}(i=1,2,…,SN)，采蜜蜂的位置对应初始解。

步骤2初始解的反向解对应于X′i={x′i,1,x′i,2,…,x′i,d}，其中x′i,i=Xmin+Xmax-xi,t(i=1,2,…,d)，比较与初始解的适应度，其中Xmin、Xmax分别为初始迭代时生成的一组初始解的下界和上界；xi,t为一组初始解中的t维分量。

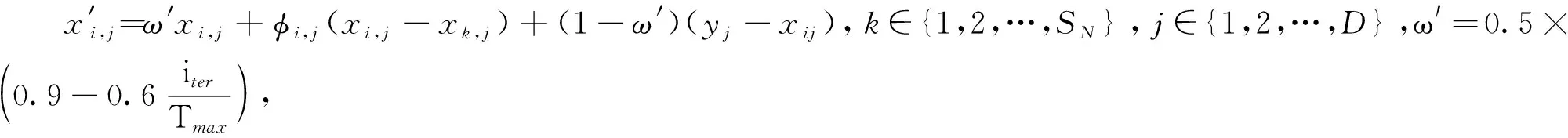
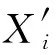
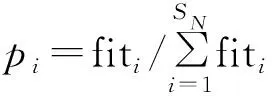
步骤6侦查蜂寻找新蜜源：xi,j=xmin,j+rand(0,1)(xmax,j-xmin,j)，其中，rand(0,1)为[0 1]之间的随机数，xmin,j和xmax,j分别为寻找蜜源遍历的最小值和最大值。

步骤7记录搜索迭代过程中发现的当前最优蜜源位置。

步骤8检查终止条件。

k为电价约束中各分时电价的编号；Limit为迭代过程中寻找蜜源的循环上限；n为机组的第n种出力计划图3 两阶段优化模型流程图Fig.3 Flow chart of two-stage optimization model

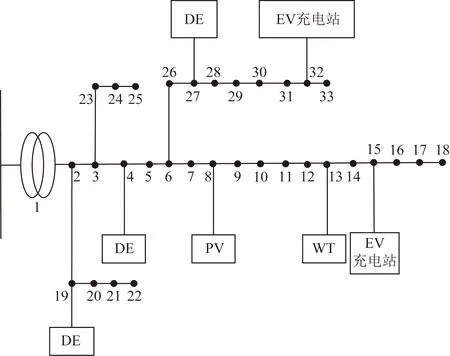
图4 IEEE 33节点系统Fig.4 IEEE 33 bus system

6 算例分析

6.1 基础数据

以IEEE 33节点系统对所提模型的有效性进行验证，系统图如图4所示。在节点4、19、27处接入柴油发电机组，机组的启停时间为3 h，机组的爬坡速率范围为0～200 kW·h，功率上限为400 kW，燃料成本系数为0.396 元/kW·h，维护成本为0.088 元/kW。在节点8处接入功率为1 200 kW的光伏组件方阵，维护成本为0.012 元/kW。在节点13处接入功率为1 500 kW的风机，维护成本为0.029 元/kW。在节点15、32处接入EV充电站，总共接入200 辆功率为24 kW的EV。

6.2 结果分析

结合风光出力和EV功率特性，综合考虑配电网对EV接纳能力和系统运行成本设定了3种典型模式，验证所提弹性调度策略的有效性。

模式1考虑配电网对EV的接纳能力最大的调度策略。

模式2考虑系统运行成本最小的调度策略。

模式3综合考虑配电网对EV的接纳能力最优和考虑系统运行成本最小的调度策略。

6.2.1 需求侧响应结果分析

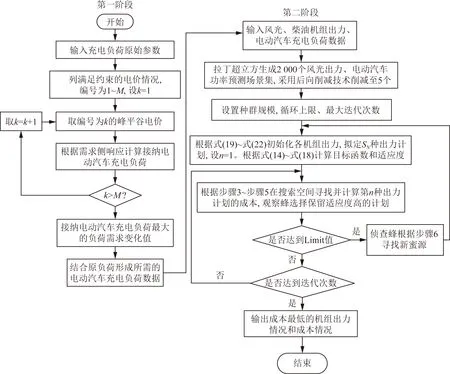
参照浙江省某市峰平谷时段的划分规律，并根据峰平谷时的价格需求弹性矩阵，以配电网接纳EV最大为目标函数，求解得到峰平谷时段电价如表1所示。图5、图6分别为EV日充电时间分布和考虑需求响应前后负荷曲线。EV充电时间主要集中在中午12:00和18:00，多采用快充模式，对于配电网接纳能力和经济性有更高的要求。实施电价型需求侧响应对负荷有“削峰填谷”的作用，在11:00—14:00和18:00—20:00高峰时段，柴油发电机组爬

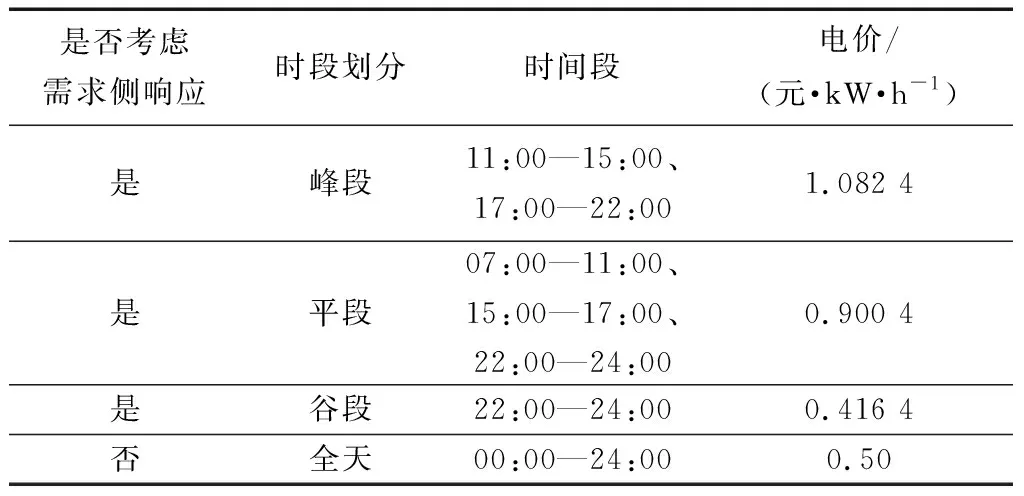
表1 峰谷分时电价Table 1 Peak valley time-sharing price

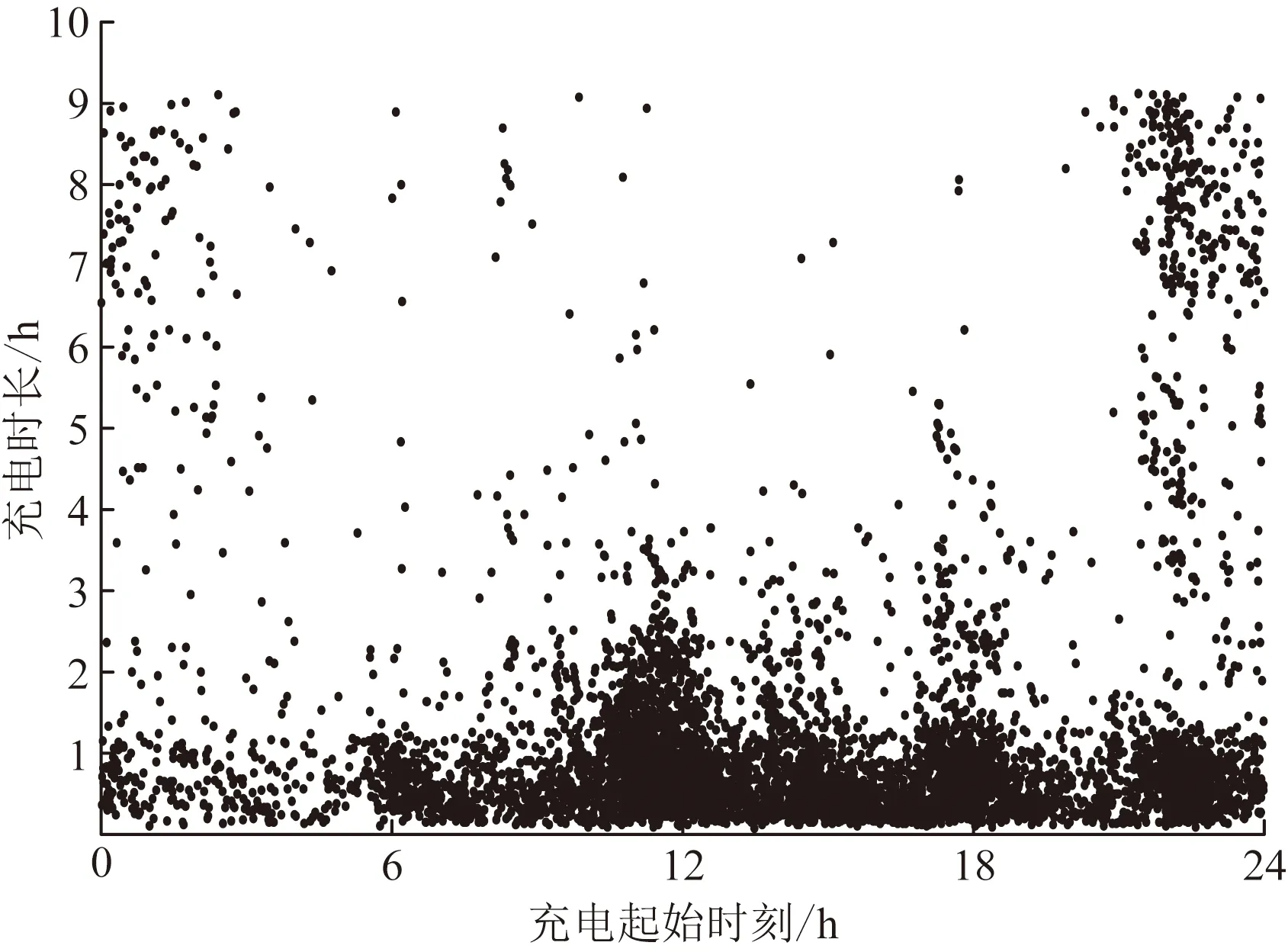
图5 EV日充电时间分布Fig.5 Daily charging time distribution of electric vehicles

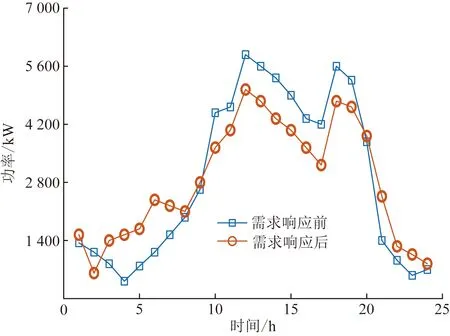
图6 考虑需求响应前后负荷曲线Fig.6 Load curve before and after considering demand response

坡压力增大，通过调整峰电价引导EV用户调整用电策略，峰荷明显减少，提高了电网的灵活性。在1:00—8:00和21:00—24:00低谷时段，柴油机组运行水平较低，EV多处于停驶状态，较低的谷电价使得用户用电负荷相对增加，缓解白天用电高峰期系统备用压力，降低EV用户充电成本，具有经济性。

6.2.2 3种调度模式结果分析

对场景1的3种调度模式下购电成本、系统运行成本以及配电网对EV的接纳能力进行研究，其分析结果如表2所示。

模式1考虑接纳能力最大，随着风电、光伏接入容量的增加，系统消纳水平下降，系统运行成本为36 254.31元，EV的最优接纳平均容量为2 200 kW。模式2考虑系统运行成本最小，向上级购电成本减小，系统运行成本为28 043.88 元，比模式1减少了22.65%，这对于提升风光利用效率和系统经济性有着显著作用，但接纳能力较差，仅为1 487.5 kW。模式3综合考虑配电网对EV的接纳能力最优和考虑系统运行成本最小，系统运行成本为28 427.04 元，最优接纳平均容量为1 866.7 kW，接纳裕度警戒频数从4 次减少到1 次，在降低系统运行成本的同时，也提高了系统的灵活性和安全性。

图7、图8显示配电网中对EV最优接纳裕度的时序变化。不考虑需求侧响应时，节点接纳裕度较小，变化范围为12%～23%，考虑需求侧响应后，最优接纳裕度接近50%，这说明需求侧响应对配电网的安全经济运行起促进作用。在3:00— 6:00柴油机组运行水平最低，EV多处于停驶状态，风电出力相对较多，此时配电网具有较高的弹性接纳裕度；12:00—13:00系统内负荷爬坡增大，EV以较高功率运行，配电网接纳裕度处于警戒区，系统承受着接纳裕度不足的风险，此刻要控制系统接入容量，避免接纳裕度进入越界区；下午14:00—17:00，系统负荷水平下降，弹性接纳裕度增加；18:00后出现晚高峰，柴油机组满载运行，接纳裕度显著下降，之后逐渐恢复。

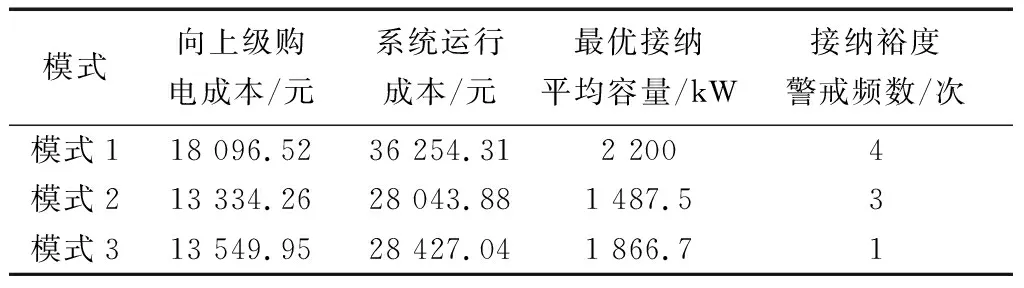
表2 不同调度模式下优化结果对比Table 1 Comparison of optimization results under different scheduling modes

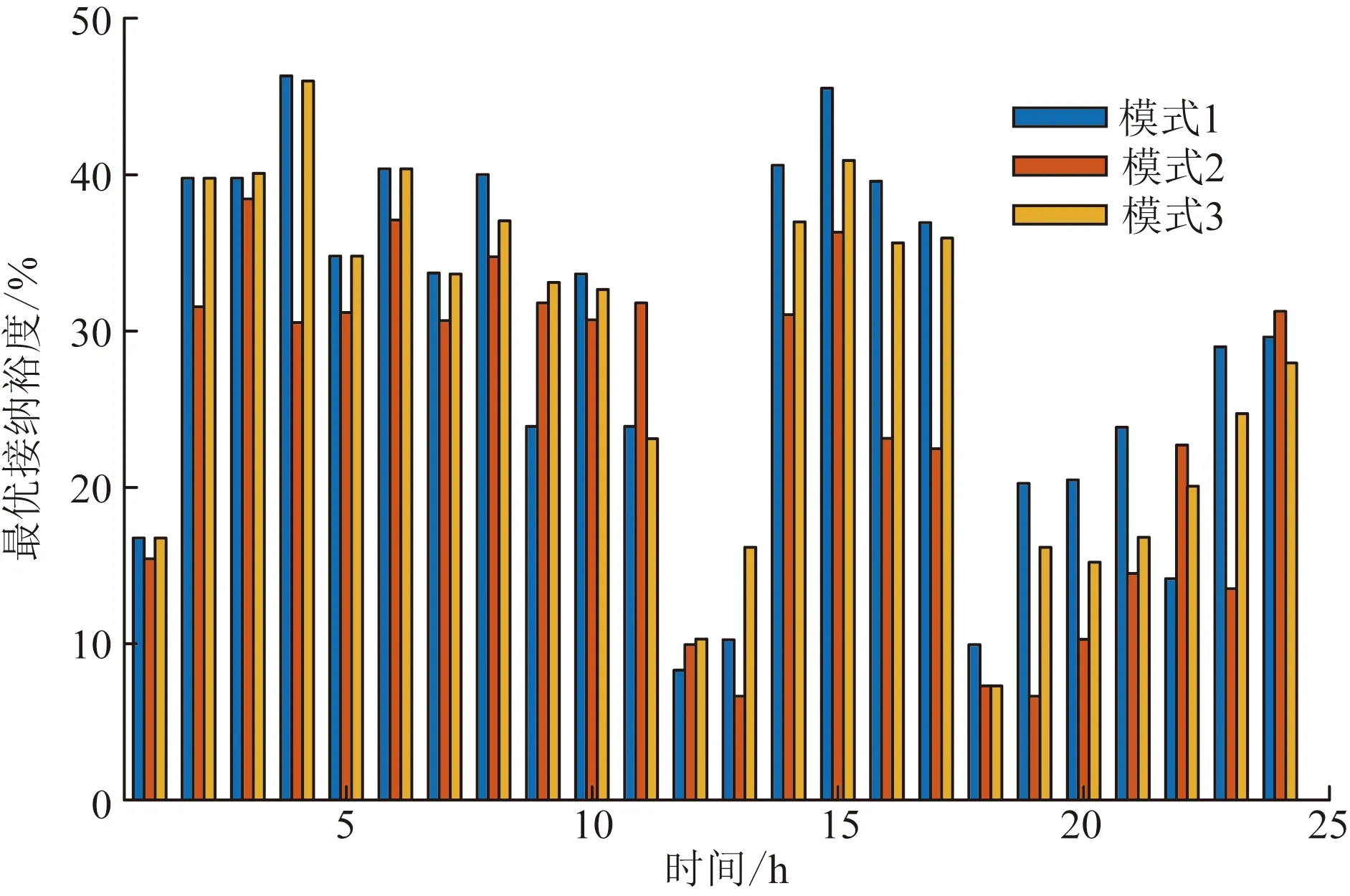
图7 3种模式下最优接纳裕度Fig.7 Optimal acceptance margin under three modes

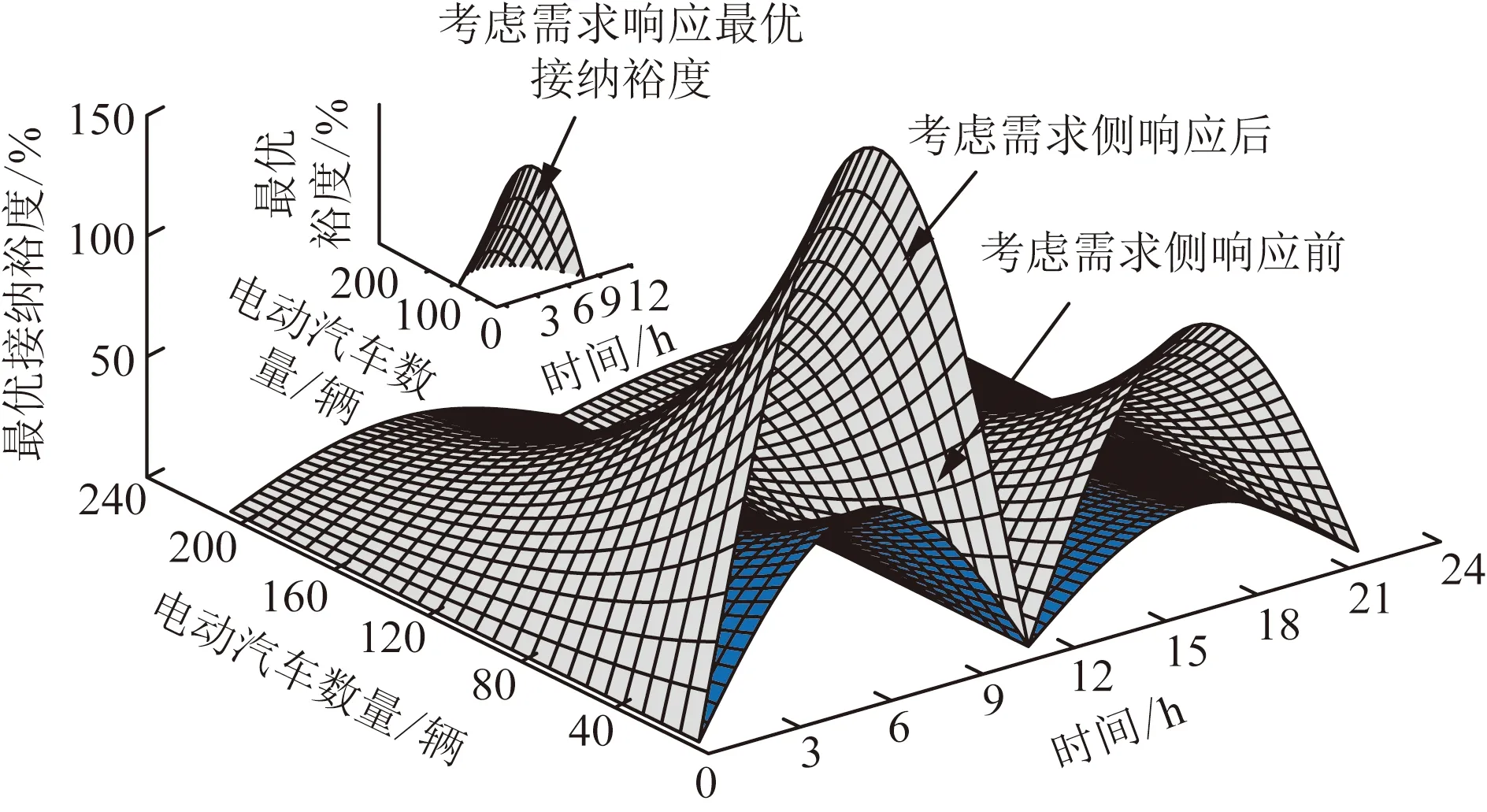
图8 需求响应前后接纳裕度变化Fig.8 Change of acceptance margin before and after demand response

图9显示在0:00—7:00谷时段，光伏、风电出力水平低，主要从上级电网购电满足负荷需求。在9:00—16:00期间用户用电量增加，光伏、风电和柴油机组成为主要供电单元，且柴油机组接近满载状态运行，除此之外仍需从上级电网购电，但系统运行成本比模式1低。所提出的调度策略有效降低了系统运行成本，提高了运行经济性。

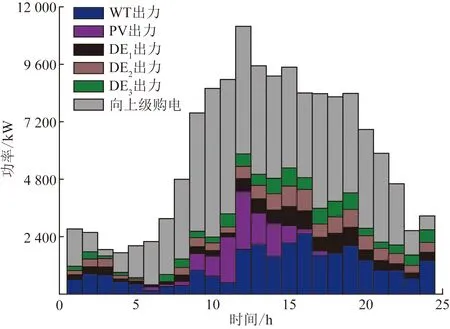
WT、PV和DEi(i=1,2,3)出力分别为在一天内风电机组、光伏机组和柴油机组出力情况图9 模式3的机组发电计划Fig.9 Unit generation schedule of mode 3

6.2.3 优化算法对比

采用改进人工蜂群算法对模型进行优化，并与粒子群、常规人工蜂群算法进行对比分析。由图10可知，改进的人工蜂群算法寻找最优解的性能更优，在第35次迭代已经收敛，具有更好的优化效果与更快的收敛速度，而粒子群和常规人工蜂群算法相对来说精度较低，收敛速度较慢。同时本文算法有利于降低系统运行成本，从最初的36 254.31 元下降到28 427.04 元，对于配电网的弹性优化调度具有更好的经济性与可靠性，更符合配电网实际情况。

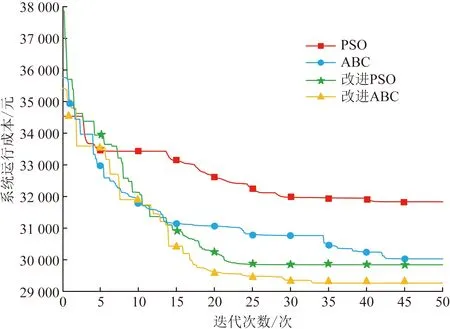
图10 优化过程收敛曲线Fig.10 Convergence curve of optimization process

7 结论

针对风、光和EV接入配电网的渐进式加剧小扰动事件对配电网弹性调度的影响，提出一种考虑风光出力和EV功率不确定性及配电网接纳裕度的弹性调度策略，设置3种典型模式并采用改进人工蜂群算法优化，最后进行算例分析，得出如下结论。

(1)综合配电网对EV的接纳裕度和考虑系统运行成本，使调度策略更符合实际运行需求，提高了系统的经济性和安全性，增强了对电动汽车的接纳能力。

(2)通过建立考虑需求弹性的EV充电站用户需求侧响应模型，利于EV负荷削峰填谷，提高了弹性配电网应对不确定性扰动的能力。

(3)采用改进人工蜂群算法和其他算法进行比较，提高优化效果，避免陷入局部最优，具有现实意义。

随着更多可再生能源和EV接入电网，考虑EV放电对配电网运行的影响和提升接纳裕度评估指标是后续研究的重点，以实现配电网弹性调度的经济性和安全性。