考虑运输成本最优化的多式联运路径选择模型

文/李蓁 魏雯

多式联运是货物流通的重要媒介，由于传统模型在预测路径选择时对成本因素考虑不足，导致多式联运路径选择的成本较高，研究考虑运输成本最优化的多式联运路径选择模型。获取道路更新数据特征，处理数据库更新道路信息。构建多式联运交通网络，连接运输转换节点。预测路径选择行为，引导路径选择，调控货运量。基于运输成本建立多式联运路径选择模型，完成路径选择。经实验论证分析，与传统模型对比，本文模型的路径选择运输成本更低，节约了40102.54元，说明本文模型具有较好的应用效果。

0.引言。

随着综合运输系统的不断发展与普及，多式联运业务也不断增多，多式联运作为一种先进的运输形式广泛地应用于现代物流行业，多式联运能够充分发挥不同运输方式的特点，具有运输效率高，涉及面广、运输成本低的特点，是提升运输服务质量的有效保障[1-3]。多式联运在国外发展已较为成熟，但在国内还处于快速发展中，国内外学者进行了较为深入的研究，本文基于运输成本为限制条件建立运输模型，为未来考虑成本的路径选择提供一定的参考。因此，根据不同货物的特点，在保证运送质量的基础上选择运输成本最低的多式联运的路径具有重要的使用价值，对今后对多式联运的路径选择研究有着现实意义。

1.考虑运输成本最优化的多式联运路径选择模型

1.1 获取道路更新数据特征

道路实体情况一直处于变化中，因此需要掌握实时道路数据的更新情况。获取数据库更新的地理特征，主要包括道路维修，河流的水量情况、建筑物修筑与拆除等信息数据[4]。道路的点特征包括新建、废除和重命名的建筑物，道路的线特征也有不同方面的更新，主要包括道路元素的重新分类和属性的变化，这种变化属于道路特征基本变化，若道路元素有部分属性发生变化则对应更新路段[4-5]。本文将每个路段作为独立的地理区域，将数据元素在每一路段显示，形成数据信息字典的形式，将更新数据与道路事件相关联，按顺序处理更新。

1.2 构建多式联运交通网络

在建模前需要对模型对应的基础交通网络进行相应的处理，为了更好地了解建模思想需要先对基础交通网络的信息进行分析。在多式联运的交通网络中，一次完整的运输过程需要经过多种方式进行运送，在相同线路中，多式联运交通会给运送方提供多种运输方式，运送货物的过程将经过多种运输方式的选择，其中包括对运送方式的选择和运送路径的选择，由于需要考虑运输成本的最优化，本文采用基于多式联运的交通运输网络。通过不同的制式的不同站点作为节点重新构建交通网络，将运送服务作为连接线，在多式联运交通网络中，将利用制式作为区分依据，使各区域形成相对独立的子网络，并以运输转换节点为连接，该网络可表示为：

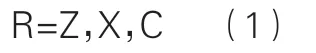
式中R为多式联运交通网络，Z为多式联运交通的集合，X表示各交通站点集合，C为各类连接线的集合。城市内部交通线网络通常采用单一轨道交通制式，在城际交通线网络采用可以兼容低级制式的高等级线网，提供多式联运的运输服务。在整体网络中用实线连接线表示运输方式的多样性，用虚线连接线表示运送路径的转换行为，使整体网络符合运输者对多式联运交通网络的理解。

1.3 预测路径选择行为

预测货物运送方对路径的选择行为是建模前的关键步骤，通过调整物流服务，引导运送方进行不同的路径选择。通过获得事件发生的预测概率，预测变量是离散的选择支，通过比较不同选择的效用，计算选择支被选择的概率。根据效用最大化的观点，预测运送方决策者将优先考虑成本为效用的最大，此选择支概率最大。根据观测到的自变量分析和描述在特定情况下的事件发生概率，给出运输成本，额外成本，运送时间等信息，得到货物运送方路径选择的概率，从而预测未来的路径选择结果。

1.4 基于运输成本建立多式联运路径选择模型

根据多式联运各运输方式的特点，船运价格最低但耗时较长，因此在时间充分的条件下可以通过船运进行货物的运送，但更多情况下，物资运送希望在时间上得到有效地保障，因此在约束条件中，时间约束是极其重要的部分，设置Kn为第n种运输方式的运输成本，Klnn´为从第n种运输方式转换为第n´运输方式时的转换成本。具体建模过程如下：

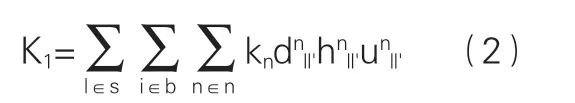
上式为始发地货物运往中转站的运输成本，其中l为原产地节点，l´为原产地中心城市，设第s个城市为中心城市；i为需求地节点，i´需求地中心城市，n为运输方式，dnll´=1为节点i到i´采用n种运输方式运输，hnll为原产地l到中心城市l´之间的运输量，unll为原产地l到中心城市l´之间的运输距离，且l≠1。在中转站中，货物运输方式的转换成本为：

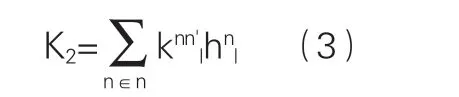
式中hnl为原产地节点货物运输量，从需求点中转站运送到需求地的运输成本为：

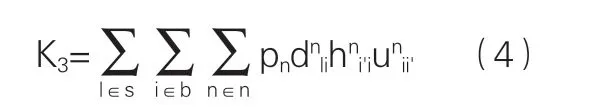
式中pn为n种运输方式的运输二氧化碳排放因子，综合上述各运输环节成本，建立总的目标函数的模型为：

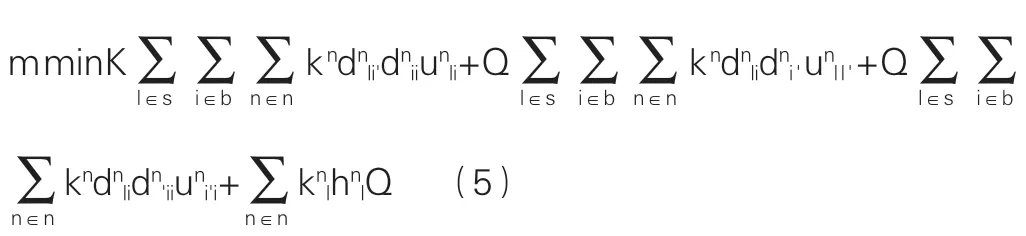
式中Q=1表示货物运输采用多式联运枢纽，式中所有参数均为非负数。接下来对成本进行分析，进行模型求解，通过模型对路径成本的变化分析，为货物运送方选择运送路径提供参考。

2.实验论证分析

本文随机选取了成都作为多式联运的出发点，设定运送货物40吨，终点为日本东京。本文基于遗传算法，求解多式联运路径选择模型成本最优路径，设计运送路径节点共13个，具体情况如图1所示。

图1 成都到东京多式联运运输网络

由图1所知，为后文表述方便，将图中城市用字母符号表示，对照字母已在图中给出。由上文运输成本函数可知，计算各运输方式的运费，不同运输工具之间的中转费用具体来源于网络收集，铁路运输成本约为0.32-0.52元（吨/千米），内陆水运为0.44元（吨/千米），国际水运为0.44元（吨/千米），航空运输为0.78-0.9元（吨/千米），不同运输工具之间中转费用如下表1所示。

表1 运输中转费用（元/吨）

由表1可知，考虑路程中换装费用不受运输距离影响，因此假设运输方式之间换装成本固定不变。运用matlab软件，编写本文采用的遗传算法程序进行求解，可求解出最优成本路径，设定上述算法参数，设交叉概率为0.8，变异概率为0.01，最大世代数为450。最终得到16个非劣解集，根据运输成本最优化的目标，本文选出了最优路径，为验证本文模型的有效性，本文选择传统路径选择模型与本文模型进行对比，具体最优路径选择情况如表2所示。

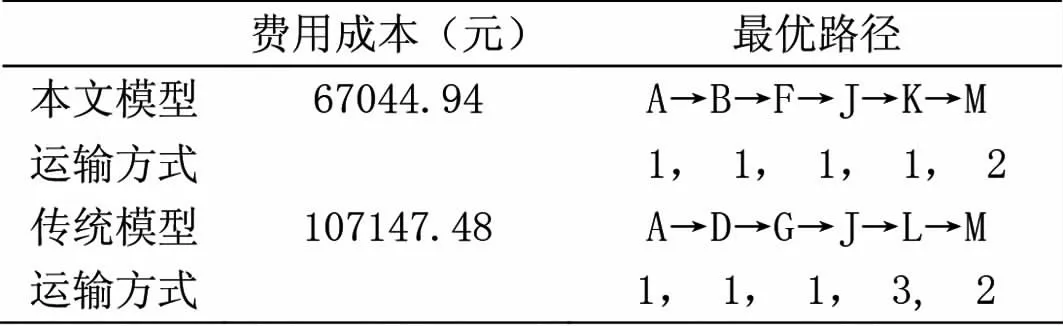
表2 不同模型路径选择最优结果

由表2可知，1代表铁路运输，2代表水路运输，3代表航空运输，本文模型选择的路径与传统模型路径相比，节约了40102.54元，说明本文模型具有有效性，可以在多式联运的基础上根据不同运送需求提供不同的联运参考方案，节约运输成本。

3.结束语。

本文以运输成本最优化为目标，获取道路更新数据特征并在数据库进行添加、修改和删除等处理，构建多式联运交通网络，预测路径选择行为，建立多式联运的路径选择模型，取得了一定的研究成果。但同时，由于时间和条件的限制，本文研究还存在着诸多不足，需要进一步探讨。本文路径选择模型中只针对成本这一影响因素做了具体研究，日后还可以考虑时间成本等因素，进行多目标优化，进一步研究更加科学的因素取值方法，提高现代物流运输的整体竞争力。C