基于CEL法的反铲挖泥船铲斗土体相互作用研究

林浩地，秦斌，邬德宇*，张其一

（1.中国海洋大学工程学院，山东青岛266100；2.中交天津航道局有限公司，天津300461）

0 引言

与绞吸、抓斗等传统挖泥船相比，反铲挖泥船是近年来发展起来的一种新型挖泥船[1]。相较于其他挖泥船，铲斗挖泥船操作简单，在疏浚作业中较为灵活，适应不同的工况条件，因此被广泛应用于疏浚工程中[2-5]。作为反铲挖泥船的主要挖掘机具，铲斗与疏浚土的相互作用影响船舶生产效率的发挥。

目前，国内外关于铲斗与土体相互作用的研究主要集中在挖掘阻力上。Kudryavtsev Ye[6]通过Mathcad软件研究单斗挖掘机铲斗摆动挖掘力，开发了计算挖掘阻力的程序；Tsuchiya Kenji等[7]通过实验提出了一种基于视觉的时空测量技术，用于估算挖掘阻力；文献[8-10]运用离散元及多体动力学等方法计算挖掘阻力，提出了相应的耦合模型计算挖掘阻力。反铲挖泥船作为水下挖泥机具与土体的相互作用较为复杂，并且挖掘过程中伴随着土体的剧烈变形。因此上述研究人员多采用实验及离散元法进行研究，且大多侧重研究铲斗旋转挖掘土体时的挖掘阻力变化规律，并未考虑反铲挖泥船开挖作业时铲斗的切入角度、挖掘深度对挖掘阻力的影响。

近年来，耦合的欧拉-拉格朗日算法（CEL）被广泛应用于土体的大变形数值模拟。姜益[11]通过CEL方法对疏浚抓斗挖掘过程进行了数值模拟，得到了相应的挖掘阻力曲线，文献[12-14]利用CEL法对涉及土体大变形的切削、插桩过程进行了模拟，并得出了较理想的结果。综上，本文将利用岩土工程软件ABAQUS，并采用CEL法，对反铲挖泥船铲斗挖掘土体的过程进行数值模拟。

1 CEL算法简介

1.1 拉格朗日法与欧拉法

拉格朗日法是固体力学中常用的方法，可以快速求解控制方程；缺点是若材料有较大的变形，网格会严重扭曲，导致计算结果不收敛[15]。欧拉法是流体力学中常用的方法，即使材料发生较大变形，网格形状也不受影响，计算结果仍能收敛；但是，当欧拉域中存在多种材料时，会发生数值扩散，不能准确捕捉材料边界[15]。

1.2 耦合欧拉-拉格朗日（CEL）算法

CEL算法结合了拉格朗日法和欧拉法的优点，网格不变形并能准确捕捉材料边界。欧拉材料与拉格朗日单元的接触通过显式通用接触实现[15]。在铲斗与土相互作用的问题中，由于土体变形严重，铲斗相对于土体的变形可以忽略不计。因此，可以采用拉格朗日法与欧拉方法分别描述铲斗与土体，两者的界面可用拉格朗日区域（铲斗）的边界来描述。

1.2.1 CEL算法的控制方程

欧拉算法中质量、动量、能量守恒方程以空间导数的形式给出，而在拉格朗日算法中采用的是物质导数的形式。两者关系如式（1）所示[16]：

1.2.2 CEL算法的接触控制

CEL算法中采用罚函数耦合算法模拟欧拉体与拉格朗日体之间的接触，防止流体侵入固体。通过拉格朗日节点和欧拉材料界面上锚定点的相对位移s确定两者的位置关系，若拉格朗日节点未侵入欧拉物质，则无需处理；反之，界面力就会分布到欧拉材料的锚定点上。界面力的大小与侵入的相对位移成正比[12]。

式中：αi为罚刚度系数，其值取决于拉格朗日和欧拉材料的特性。

2 数值模型及计算工况

2.1 数值模型

为研究反铲挖泥船挖掘过程中铲斗与土体的相互作用，分别建立土体和铲斗的三维模型（图1），铲斗设置为拉格朗日体，斗口尺寸为D×B。土体采用欧拉模型，为减小边界效应，土体尺寸取10D×6D×4D。为确保计算结果的精度及计算效率，本文对局部网格进行细化，细化区域网格尺寸为0.05D[13]。土体采用EC3D8R单元，共划分309 120个单元。在土体被挖掘的过程中，被挖掘部分会被铲斗带离土体，因此需要在土体上方设置一定高度的空隙层，避免土体流出边界。

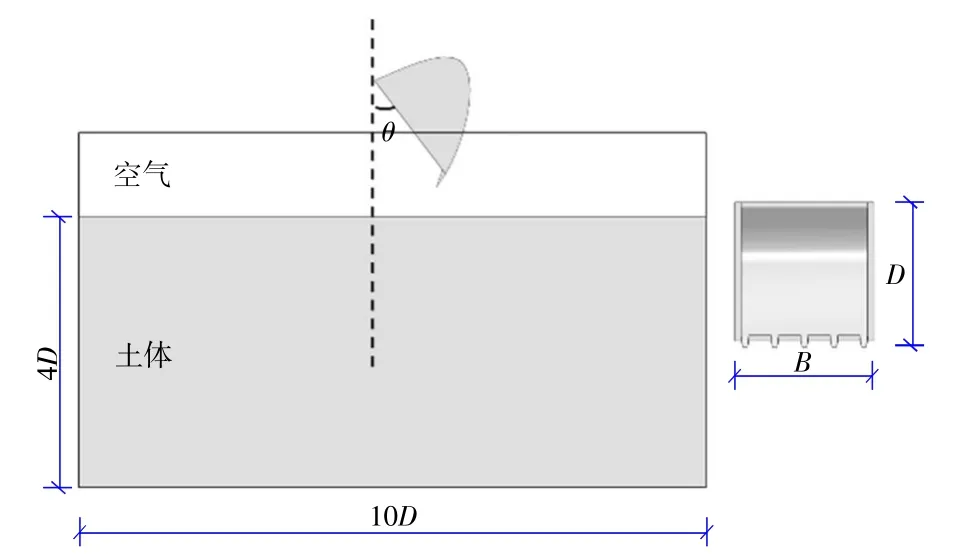
图1 土体与铲斗模型Fig.1 Soil mass and bucket model

欧拉节点不随材料流动，需要在欧拉节点上使用指定的速度或加速度条件来控制物质流动[16]。本文在计算过程中约束土体四周边界材料的法向流动速度以及底部边界材料的所有方向流动速度。

考虑到铲斗的刚度远远大于土壤的刚度，在分析过程中将其视为刚性体。铲斗的平面运动通过铲斗上的刚体参考点控制。土体采用弹塑性模型模拟，其物理力学参数见表1。在ABAQUS中弹塑性模型的弹性部分和塑性部分是分开定义的，弹性部分采用基于广义胡克定律的线弹性模型，塑性部分采用扩展的线性Drucker-Prager模型[15]。

表1 土体的物理力学参数Table 1 Physical and mechanical parameters of soil mass

2.2 计算工况

为了研究切入角度、挖掘深度对土壤的变形及挖掘阻力变化规律的影响，本文假定在各个工况中铲斗下降切入土体的速度以及旋转速度都是一致的。切入角度及挖掘深度见表2、表3，其中工况1～6挖掘深度为h=0.5D；工况7～12切入角度θ=30°。铲斗的最大旋转角度α由切入角度θ确定，即α=θ+90°。

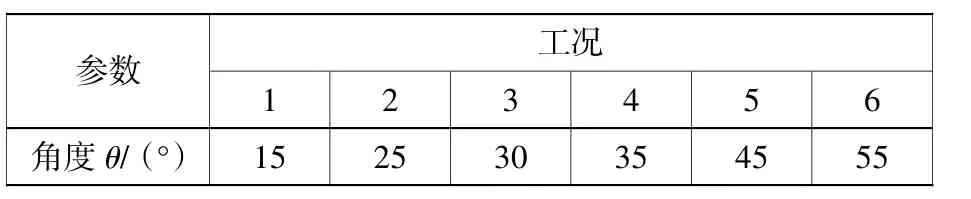
表2 切入角度Table 2 Cutting angle

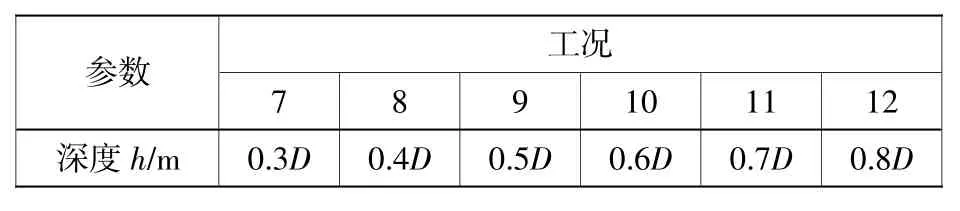
表3 挖掘深度Table 3 Excavation depth

3 数值模拟结果分析

3.1 土体变形分析

3.1.1 铲斗下降时的土体变形

由图2（图中d为铲斗实时下降深度）可以看出在铲斗下降进入土体过程中，铲斗外侧与土体的接触面积逐渐增大，并不断挤压土体；在这一过程中土体主要受到铲斗外侧的挤压而破坏，而斗齿的切削作用并不明显。因此实际疏浚作业时，可以选择较大的切入角度以减小在下降过程中铲斗外侧与土体的接触面积，加强斗齿的切削作用。

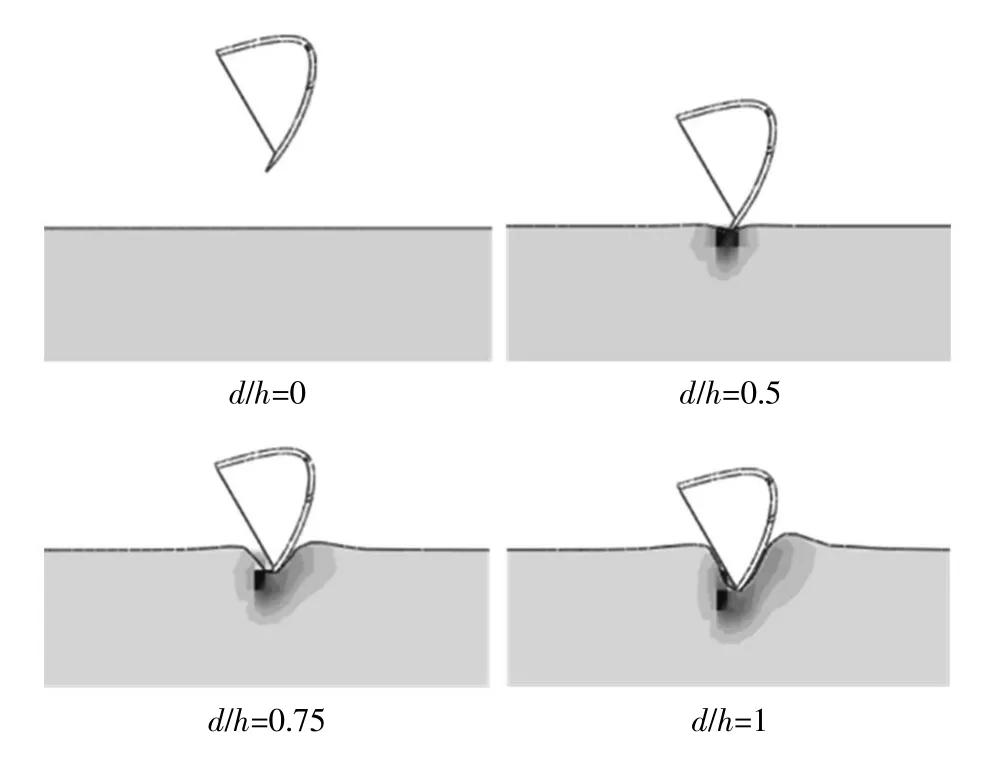
图2 铲斗下降土体的破坏情况Fig.2 Damage of soil mass during bucket lowering

3.1.2 旋转挖掘时的土体变形

由图3（φ为铲斗实时转角）可以看出在旋转挖掘过程中，土体的塑性形变主要分布在铲斗的内外两侧。泥线附近的土体在铲斗旋转挖掘的过程中基本未被破坏，只是随下层土体一起被铲斗挖起。因此在实际挖掘时，可以适当控制挖掘深度，使铲斗在挖掘时可以切削相对较软的土层减少铲斗的磨损。

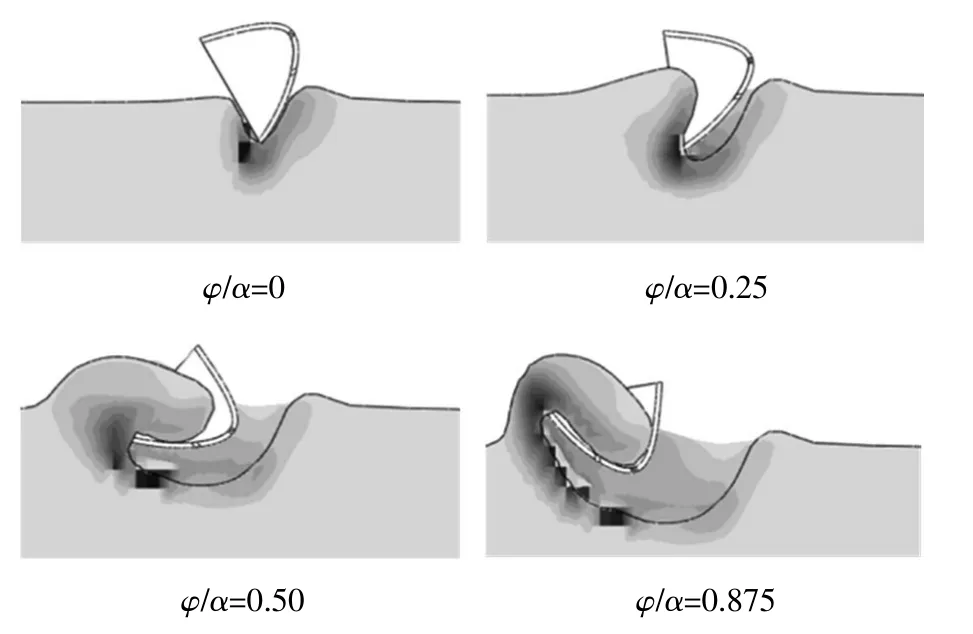
图3 铲斗旋转土体的破坏情况Fig.3 Soil failure during bucket rotation

3.2 挖掘阻力分析

3.2.1 切入角度对挖掘阻力的影响

由图4（a）可以看出，铲斗以不同角度下降切入土体时，挖掘阻力的变化规律是一致的。θ＜30°时，随着切入角度的增加，挖掘阻力明显增大，挖掘阻力的变化速率减小；θ＞30°时，随着切入角度的增加，挖掘阻力变化缓慢。

由图4（b）可以看出，铲斗以不同角度旋转挖掘土体时，由于铲斗内侧土体在铲斗下降过程中已经被破坏，因此铲斗在旋转挖掘土体初期挖掘阻力变化较缓；铲斗旋转到一定角度，内侧的土体被聚拢，挖掘阻力逐渐增大，当被破坏的土体的范围扩展到泥线附近，挖掘阻力逐渐减小；铲斗受到的最大挖掘阻力随着切入角度的增大而增大，但最大挖掘阻力基本都出现在φ/α=0.4左右；挖掘阻力在上升阶段的变化速率随切入角度的增大而增大，然而在下降阶段，挖掘阻力的变化速率几乎不受切入角度的影响。

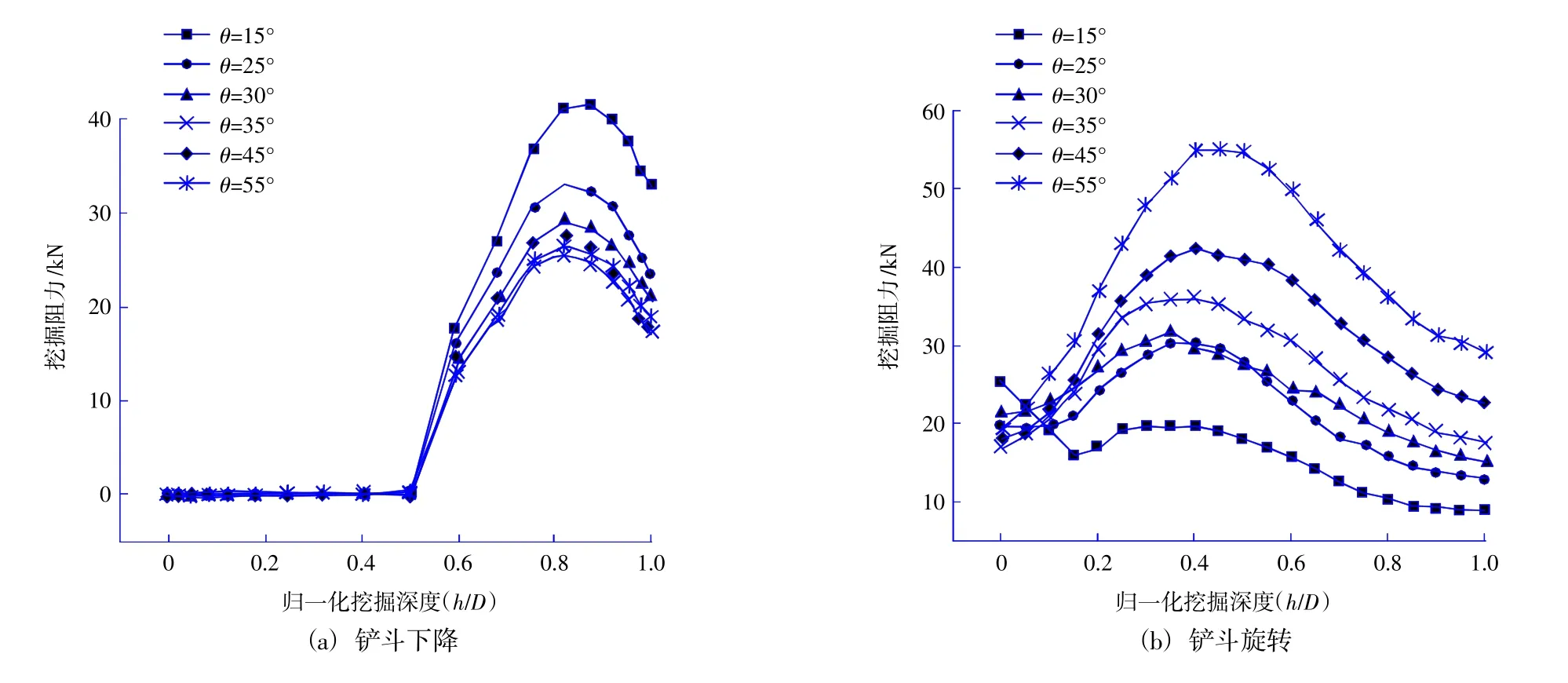
图4 不同切入角度下挖掘阻力变化情况Fig.4 Variation of excavation resistance under different cutting angles

对于工况1（θ=15°）结合图2可知，铲斗在下降过程中主要受到铲斗外侧土体的挤压，且铲斗与土体接触面积较大导致挖掘阻力较大，但这部分土体并不是被挖掘土体，所以开始旋转挖掘时挖掘阻力会减小。

3.2.2 挖掘深度对挖掘阻力的影响

由图5（a）可以看出铲斗下降切入土体时，随着挖掘深度的增加，铲斗受到的最大挖掘阻力随之增大，挖掘阻力的变化速率几乎不随挖掘深度的增大而变化。

由图5（b）可以看出铲斗旋转挖掘土体时，随着挖掘深度的增加，铲斗受到的最大挖掘阻力随之增大，且最大挖掘阻力出现在φ/α=0.4左右；不同的挖掘深度对挖掘阻力的变化速率基本没有影响。

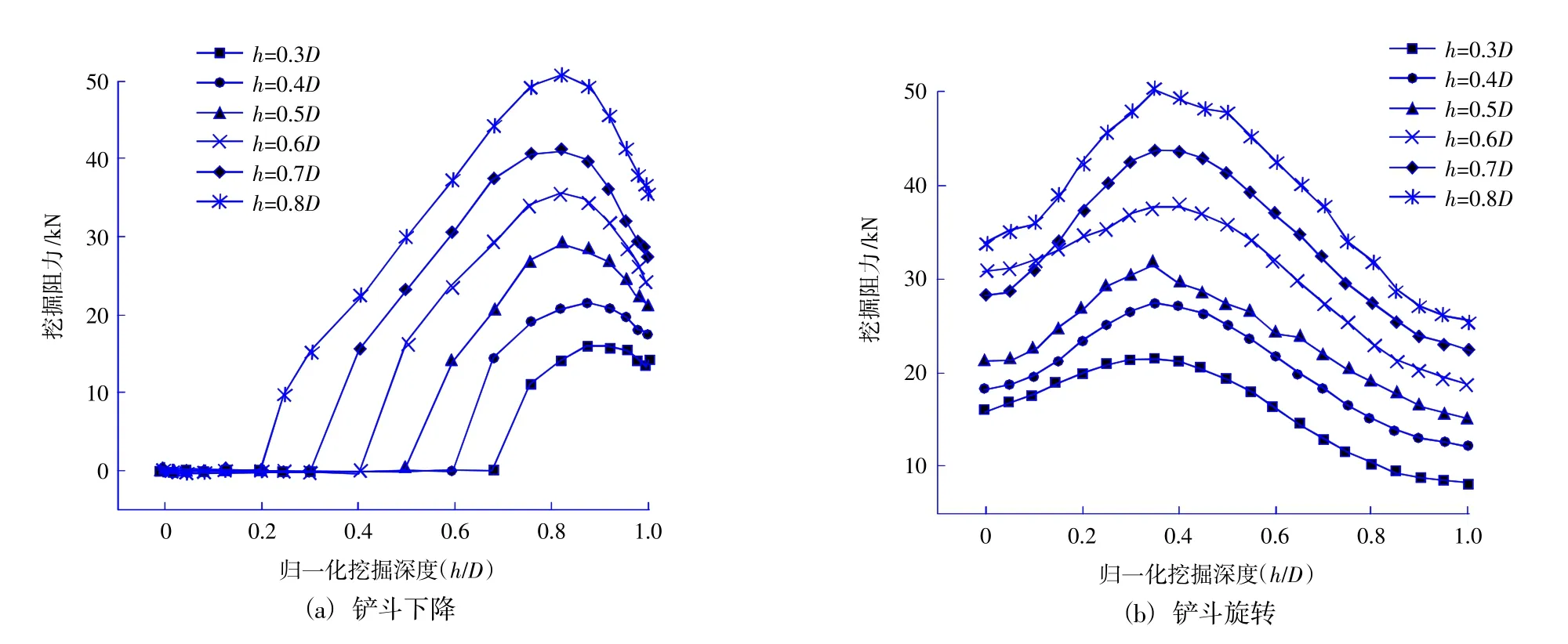
图5 不同挖掘深度下挖掘阻力变化情况Fig.5 Variation of excavation resistance under different excavation depths

4 结语

本文采用CEL方法对铲斗与土体的相互作用进行数值模拟，获得了挖泥船铲斗挖掘过程中土体的变形情况以及铲斗挖掘阻力变化规律，得到如下结论：

1）铲斗下降切入土体时，在切入角度小于30°的情况下，挖掘阻力随切入角度的增大而减小；在切入角度大于30°的情况下，挖掘阻力变化缓慢。

2）铲斗旋转挖掘土体时，切入角度、挖掘深度对挖掘阻力的变化规律影响不明显，挖掘阻力先增大后减小，当旋转角度为最大旋转角α的40%左右时挖掘阻力最大。