基于离散元的废弃宕口边坡稳定性分析

匡俊，陈芋如，朱仁民，曹建林，居俊，唐强*

（1.江苏苏州地质工程勘察院，江苏苏州215011；2.江苏地质矿产局第四地质大队，江苏苏州215004；3.苏州大学，江苏苏州215131；4.常熟理工学院，江苏苏州215500）

0 引言

近年来，随着计算机技术的飞速发展，滑坡等地质灾害的演化规律及控制取得了一系列重要成果和突破。低成本高效率的仿真技术发展和应用对于预防和控制此类灾害有显著效果[1-4]。吕文斌等[5]以西宁市张家湾某滑坡为研究对象，结合极限平衡法以及Midas/GTS有限元分析方法，研究了滑坡形成机理和发展过程，定量评价了该滑坡3种不同工况条件下的稳定状态。李效萌等[6]采用折线滑动法计算滑坡稳定性系数等方法，对滑坡在2种工况下的稳定性进行了定量探讨，在此基础上分析了滑坡成因和可能的失稳破坏模式。刘洪波等[7]基于有限差分方法建立滑坡三维模型，分析了边坡剖面、剪切带处土颗粒位移场分布后发现：当土体完全失稳时剪切带完全贯通，滑移体内土体向下加速滑动。寇甄涛等[8]对秦岭某滑坡研究分析后表明：饱和工况下坡体将失稳，坡体失稳时基岩面附近滑动面最先发生剪切破坏。

离散元技术因其能够有效模拟滑坡机理而引起众多学者的关注。王焘[9]针对滑坡堵江预判问题，分析了滑坡体方量与堵江程度相关关系。一些学者[10-17]对滑坡破坏方式及发展过程进行模拟研究，结果与实际情况基本吻合。

本文应用离散元技术模拟凤凰山弃土场边坡破坏过程，对关键部位的位移、应力进行分析，研究其变形破坏机理。

1 工程概况

苏州市科技城凤凰山弃土场位于高新区元方路和逢春路交叉口西侧，原凤凰山采石宕口。场区所在地的原始地貌属苏州西部低山丘陵，山体高度在10～130 m，自然坡度在18°～25°。经采石开挖后宕口边坡发生较大变化，边坡多在14°～58°之间，局部呈小范围直立状，宕口地形西高东低，宕口填土边坡分为南北两部分。南侧边坡坡度较北坡缓，局部较陡，在其坡脚有水渗出，形成溪流，该坡局部存在明显的雨水冲刷坍塌现象。北侧填土边坡整体为一坡到底，局部见明显的蠕滑破裂缝隙，宽度在5～20 mm左右。南、北边坡面未见岩石裸露，无滚石、崩塌等不良地质作用。勘探期间测得场地各勘探孔孔口高程在14.20～44.95 m之间，地势起伏大。图1为边坡的地质剖面图。

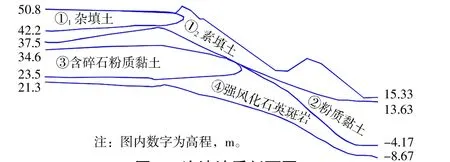
图1 边坡地质剖面图Fig.1 Geological profile of the slope

由图1可知，边坡土层间有成分为粉质黏土的软弱夹层，粉质黏土构成边坡失稳变形的潜在滑动面。边坡前缘开挖卸荷引起坡面临空，应力场发生变化，形成的不稳定块体极有可能发生滑移破坏。当变形达到一定程度时，坡面将产生裂缝，发生失稳破坏。由于松散体为均质体，各个颗粒在各方向的抵抗能力相同，滑动沿着力矩相同的轨迹滑出，形成圆弧形滑动面。

图2为凤凰山现场勘探结果。由于碎石上部覆盖大量植被及土壤，土体的黏聚力显著增大，这延缓了边坡失稳破坏需要的时间，破坏形式表现为渐进式的蠕动变形。边坡上出现的多处裂缝表明，该处边坡正处于滑移过程之中。一旦受到雨水冲刷等外界作用，边坡将迅速发生破坏，有可能造成安全隐患。为近一步研究边坡的稳定性，本文利用离散元软件对边坡的破坏过程展开数值分析。

图2 现场踏勘资料Fig.2 Site investigation data

2 边坡破坏过程数值模拟

2.1 模型建立

采用离散元技术模拟边坡滑动，在建模过程中，ball-ball接触与ball-facet接触会贯穿始终，线性模型具有较好的模拟效果。根据杜永斌[18]的研究，线性模型接触力通过成对出现并相接触颗粒之间恒定法向和切向刚度的线性弹簧产生，假设法向刚度与切向刚度之比为1，两种刚度的计算公式如下：

式中：Kn为两个接触颗粒间的法向接触刚度；Ks为切向接触刚度；A为颗粒间的接触面积；E为杨氏模量；L为两个颗粒的半径之和。由于本文中的地下水处于滑移面下方，根据何倩等[16]和宋浩燃等[17]的研究，此时地下水对于边坡滑移影响较小，因此在本次模拟中忽略其影响。本次模拟主要接触参数具体取值如表1所示。

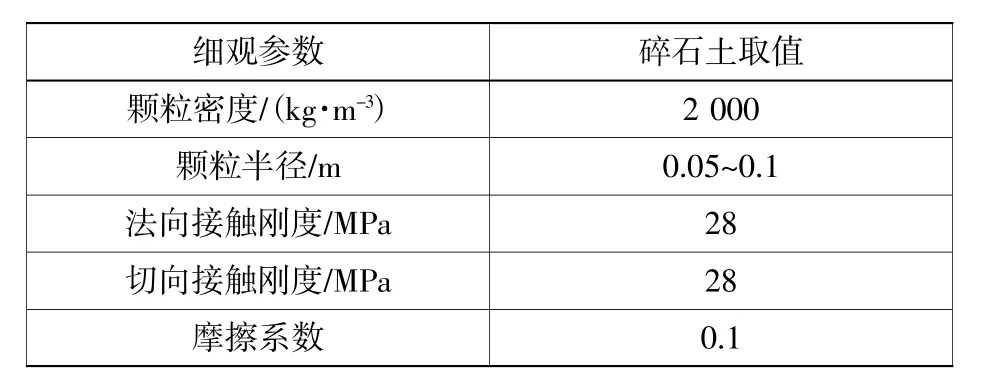
表1 碎石土的细观参数Table 1 Mesoscopic parameters of gravelly soil

模拟具体步骤为：成样，预压，加自重以及切坡。首先采用预压来释放试样中过大的内应力，随后放大重力场。在程序中经过多次重力加速度的调整，最终在80倍的重力加速度下，颗粒能够向下自然滑落。在加自重前进行了土体平衡，并定义了边坡底部坐标。

颗粒流模型计算的下部边界是有限的。颗粒流模型高度应大于地基的塑性区开展深度，即H＜Zmax，塑形区的最大开展深度为：

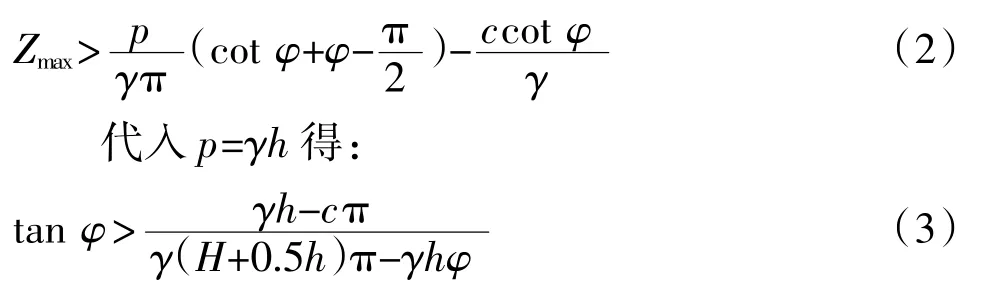
式中：p为地基的条形均布荷载；γ为土体容重；h为边坡高度；H为模型高度；c为土体的黏聚力；φ为土体的内摩擦角。

为确保滑动剪切面出现在边坡内，边坡模型最终满足H≥1.5h的条件。根据式（3），建立模型长40 m，高20 m，颗粒最小半径为0.05 m，最大半径为0.1 m，颗粒总数为64 892个。最终得到滑坡数值计算模型。图3为滑坡数值计算模型及监测点。

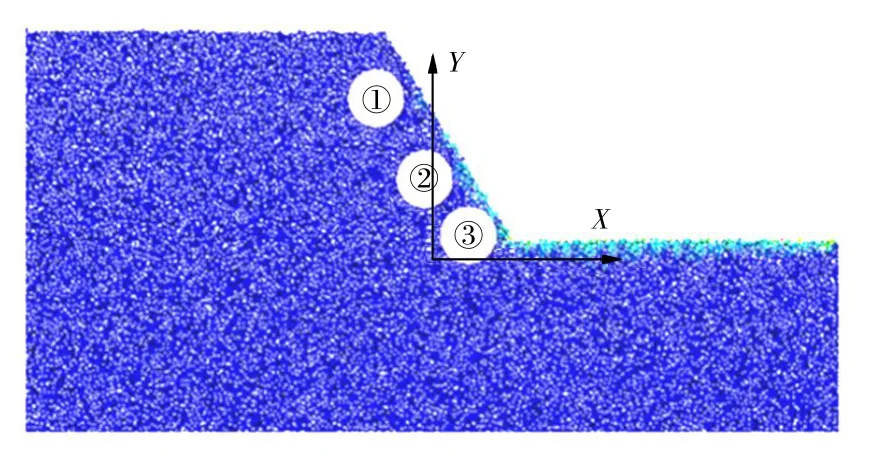
图3 滑坡数值计算模型及监测点Fig.3 Numerical landslide model and monitoring points

2.2 临界坡脚确定

凤凰山弃土场的边坡多在14°～58°之间，经过程序多次模拟，当坡角为30°时，边坡未发生滑动位移。当坡角为35°时，边坡有大部分颗粒滑落。而在选择32°坡角时，边坡只有少量颗粒发生了较大位移，边坡达到极限平衡状态，即该边坡发生滑动的临界坡角为32°。图4为临界坡角的计算云图。

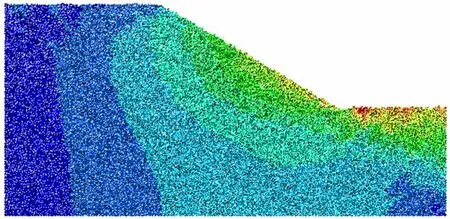
图4 临界坡角的计算云图Fig.4 Calculation clouds for critical slope angles

2.3 坡度最大处失稳过程分析

2.3.1 位移矢量分析

经实地踏勘，现场坡角最大值为58°。由于蠕动变形，边坡坡顶已出现明显的裂缝。通过数值模拟对该处边坡的失稳过程进行分析。

位移是边坡发生破坏的直观表现，由图5可知，该边坡的失稳模式是蠕动性滑坡。计算初始，边坡开始变形，靠近坡面的颗粒逐渐滑落，岩体蠕动变形。随着时间的推移，颗粒滑动位置往坡内移动；当计算到10 s时，剪切带基本贯通，形成稳定斜坡，滑动面呈圆弧状，坡趾圆也基本形成；当t=30 s时最终平衡，颗粒的最大位移达10.4 m。

图5 边坡破坏过程模拟Fig.5 Simulation of the slope failure process

2.3.2 应力变化分析

在斜面上设置3个监测点，以观察对比斜坡顶部、中部以及底部的应力变化。监测点的具体位置以及名称序号如图3所示。监测曲线图如图6所示，分别监测斜坡x方向正应力（σx），剪应力（τxy），以及y方向的正应力（σy）。

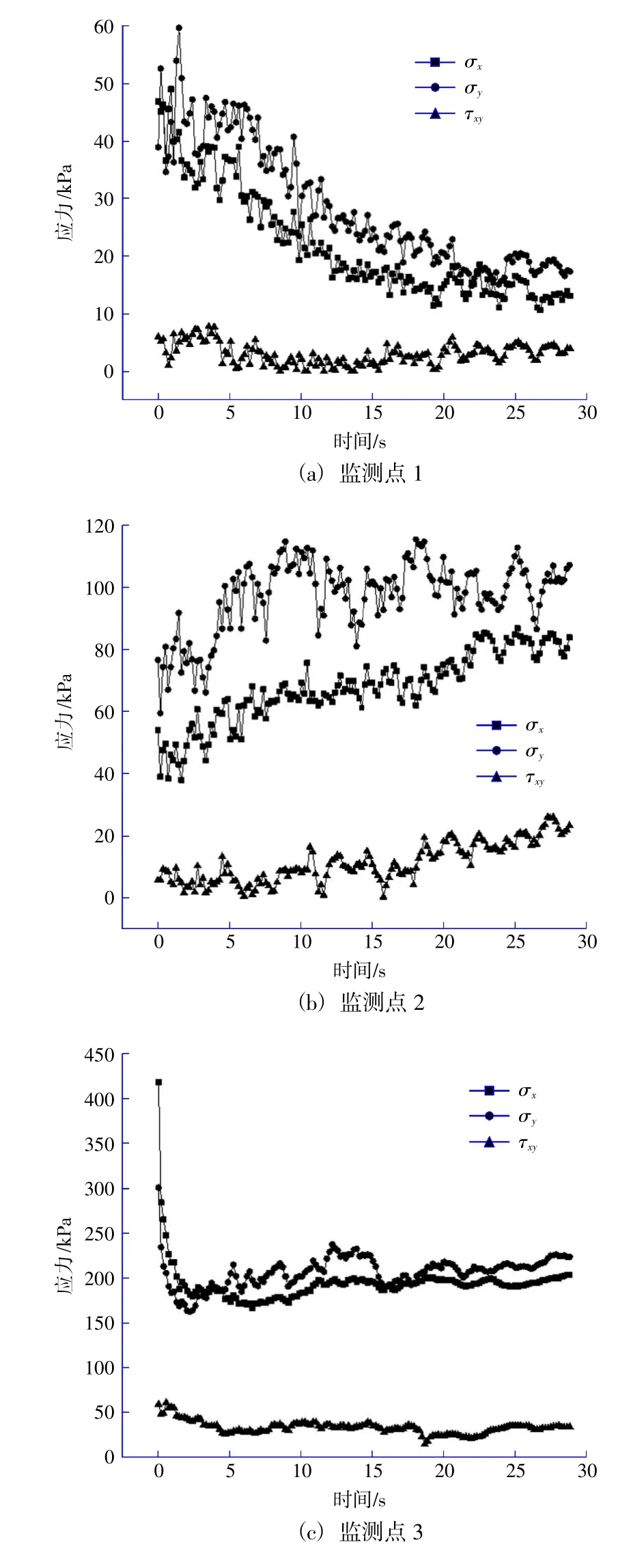
图6 应力变化曲线Fig.6 Curves of stress changes

由图6可知，监测点1处的颗粒在模拟过程中位于坡体的顶部，并不断发生向下的位移，因此此时的应力曲线呈总体减小趋势。

相反，监测点2处的x，y方向正应力以及剪应力均呈上升趋势，且y方向的正应力与x方向正应力相比较大。这是因为斜坡中部随着变形量的增加，不断受到碎石土向下的挤压，颗粒不断堆积，导致y向应力逐渐增加，峰值应力为115.24 kPa。

坡脚处的监测点在滑动初始阶段应力骤降，随后趋于平缓，这是因为坡脚处在一开始的滑动过程中，颗粒间不断调整位置，发生剪切破坏。随着上覆土体的不断滑下，监测点1处土体被上覆土体覆盖，坡体滑动对其影响减小，坡脚处达到应力平衡。剪应力在整个滑动过程中变化幅度不明显，坡脚的剪应力最大值为70.84 kPa。

2.3.3 结果讨论

根据瑞典条分法，边坡的安全系数可以由公式（4）进行计算：

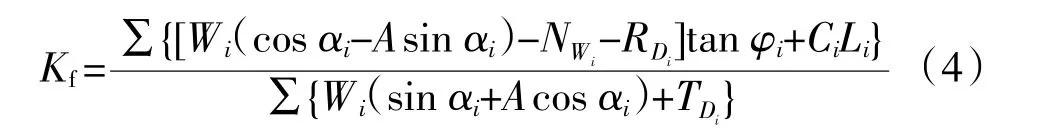
式中：NWi为孔隙水压力；TDi为渗透压力产生的平行滑动面分力；RDi为渗透压力产生的垂直滑动面分力；Wi为土体自重；Ci为土体内聚力；φi为土体内摩擦角；Li为滑动面长度；αi为滑动面倾角；A为地震加速度；Kf为稳定系数。

根据石崇[19]的研究，植被根系及黏土含量的增加会增大边坡填土的黏聚力。公式（4）表明，黏聚力的增大会显著提高土体的抗滑力，提升边坡的稳定性。在黏聚力的作用下，该边坡缓慢发生蠕动变形。一旦受到雨水冲刷等外界作用，土体的黏聚力将迅速减小，边坡容易发生失稳破坏。

3 结语

本文通过离散元技术对苏州市科技城凤凰山弃土场边坡稳定性进行了模拟，得到以下结论。

1）边坡达到32°的坡角时，达到极限平衡状态。从现场勘探情况看，最大坡角处边坡已经出现明显的裂缝，可以通过削方减载、挡土墙法、抗滑桩法、格构锚杆法等来实施滑坡整治措施。

2）模拟现场最大坡角58°处的边坡过程中，随着时间的推移，颗粒滑动的位置向斜坡内部移动，滑动剪切带基本形成并贯通以后，颗粒发生塑形流动，形成稳定的圆弧形滑坡面。

3）坡体中部颗粒的正应力由于不断受到上覆颗粒的挤压呈非线性增长，坡脚位置处的应力呈总体下降趋势，随着时间的推移最终达到平衡。