重力式锚碇基础的稳定性数值模拟研究

刘旭，吴锋，邵国建，苏静波，徐洪钟

（1.中交上海港湾工程设计研究院有限公司，上海200032；2.河海大学，江苏南京210098；3.南京工业大学，江苏南京211816）

0 引言

早期的重力式锚碇结构均建造在岩石基础上，如美国的乔治华盛顿大桥和旧金山奥克兰湾大桥等。然而当岩基的深度很大时，将锚碇直接建在岩基上会导致造价成本高昂。因此在岩基较深的锚碇基础工程中，设计人员尝试着将锚碇直接建造在土基中，如日本的明石海峡大桥与中国的江阴长江大桥[1]等。本工程案例的设计是基于现行的规范与已有工程的经验方案，现行规范中锚碇基础的评估方法是基于二维的极限平衡法。规范中分别以抗滑动与抗倾覆稳定性系数来评价锚碇基础的稳定性，然而这只是一种简化的平面假设，锚碇基础本身的失稳模式并不一定是单纯的滑移或者倾覆，真正的失稳模式是两者的组合。此外，因为二维平面假设中并没有考虑到前侧与后侧土体对锚碇基础的作用，而且锚碇基础是一种长宽高比例相近的三维块体，所以规范中的稳定性评估方法会导致计算出来的安全系数偏小。因此，有必要采用符合实际情况的三维分析来辅助确定锚碇基础的设计方案。土基重力式锚碇的已有研究内容主要是基于缩尺模型试验与数值模拟[2-3]，但是很少运用强度折减法进行三维分析来评价锚碇基础的稳定性，本文将通过强度折减法分析各种因素对土基重力式锚碇稳定性的影响。

本案例是世界上第一座单跨超过1 000 m的三塔两跨悬索桥。大桥的北桥为两跨，其跨径组合为1 080 m+1 080 m，北桥的南锚碇尺寸如图1所示。本文以该悬索桥为工程背景，结合缩尺模型试验与有限元数值分析探讨重力式锚碇基础的稳定性问题。

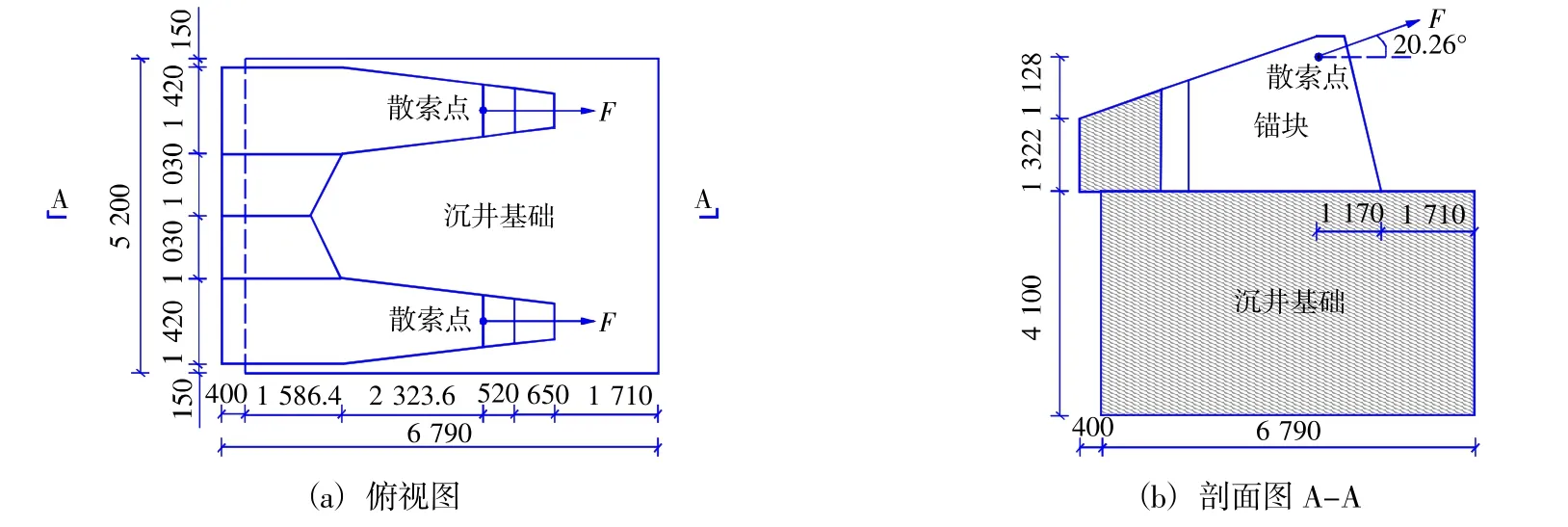
图1 锚碇结构图（cm）Fig.1 Structural drawing of the anchorage（cm）

1 缩尺模型试验

由于重力式锚碇基础的失稳机理复杂，因此需要采取缩尺模型试验来辅助实际工程的设计方案。本试验中的相似土取自实际工程周边区域，土体类型为粉砂，其主要成份为石英与长石等，粉砂的相关试验参数列于表1中。

表1 模型试验中的土体参数Table 1 The soil parameters of the model test

该缩尺模型的原始研究目的之一是通过改变锚碇基础的埋置深度来探讨锚碇周边土体对其稳定性的影响。试验表明，未埋置在土中的锚碇基础所能承受的极限拉力约占埋置在土中时的86%。本文中埋置在土中时的锚碇基础试验数据被用于校准数值模型。该模型为原型锚碇尺寸的1/50，包括1个长方体试验槽、2个固定的锚座、1个龙门架、1个固定于龙门架上的定滑轮、砝码与钢缆，具体如图2所示。

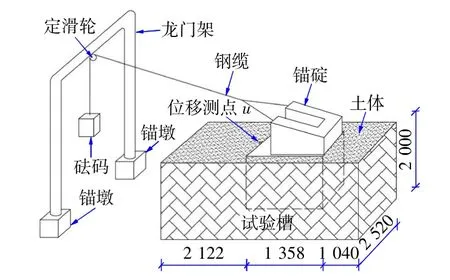
图2 模型试验的设置（mm）Fig.2 The setup of the model test(mm)

为了减小边界的影响，试验槽的内部设置为4.52 m×2.52 m×2 m（长×宽×高），分别对应于原型尺寸226 m×126 m×100 m（长×宽×高）。该尺寸能够保证锚碇基础边缘至试验槽边缘的距离大于锚碇基础本身宽度的一半。此外，试验槽的内表面布置土工膜用于防渗。

施加于钢缆上的拉力由t（t=1.61 kN）以增量t（1.61 kN）增加到14t（22.54 kN）。位移计放置于锚碇前墙的顶部并标记为u，如图2所示。锚碇前墙的横向位移在评估锚碇的稳定性时是一个重要的参考指标，在本文中用于校准数值模型。在进行加载时，每一个增量步相对应的横向位移u都会通过记录位移计的读数来获得。为了尽量使位移精准，在每一次加载时，位移计的读数需要稳定并保持5 min后再记录数据。

2 有限元模拟校准

锚碇数值分析采用ABAQUS有限元软件，数值模型中力、约束条件的施加和尺寸都关于轴线A-A对称（图1）。因此在建模时只针对半个模型进行分析。数值模型的区域、尺寸与坐标见图3。

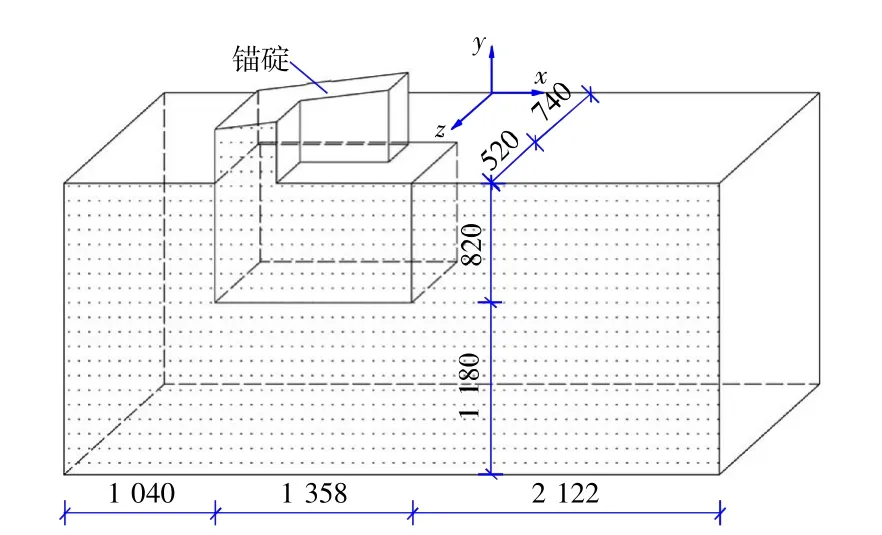
图3 锚碇数值模型的模拟区域（mm）Fig.3 Simulation area of anchorage numerical model(mm)

本数值模型采用的是八节点六面体线性减缩积分单元（C3D8R）。土体假设为各向同性的均质材料并服从Mohr-Coulomb强度准则[4]，锚碇部分假设为弹性体。在整个模拟过程中暂不考虑地下水的作用。锚碇与土体之间运用的是ABAQUS中的面对面离散方法来设定主从面，接触跟踪方法选取为有限滑动。整个分析过程可分为2步，第1步为通过地应力平衡来建立初始地应力，第2步对锚碇施加斜拉力，拉力范围为t（1.61 kN）至14t（22.54 kN）。测点读数u作为试验中的位移数据，并与数值模型中的位移数据进行对比，如图4所示。从图中可以看出数值模型的计算结果与模型试验的测量结果虽然有差异，但是趋势基本保持一致。

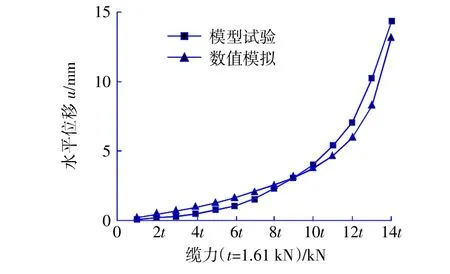
图4 模型试验与数值模型的锚碇前墙横向位移值对比Fig.4 Comparison of lateral displacement of anchorage front wall between model test and numerical model

3 工程案例

结合苏锡常南部高速公路项目，基于校正的数值模型对原型重力式结构进行分析。缆力为原型锚碇的设计拉力430 MN。施加缆力后的位移场如图5所示，从图中可知，锚碇的倾覆旋转点并不在规范中假设的脚趾处，而是在锚碇基础的底部，说明基底前侧存在一定范围的抗力。此外，通过强度折减法分析的重力式锚碇基础失稳状态（如图6所示），由等效塑性应变所表示的失效面与近海重力式平台的失效面基本吻合，失效面呈穿越重力式结构底部的弧形区域。

图5 施加设计拉力后数值模型的位移场Fig.5 Displacement field of numerical model after application of design tension

图6 锚碇失稳时土体的等效塑性应变云图Fig.6 Equivalent plastic strain nephogram of soil mass when anchorage is unstable

4 参数敏感性分析

本节将基于三维数值模型与强度折减法进行锚碇稳定性的参数分析，分析过程中只单独改变某一参数来评估锚碇基础的稳定性。目前未见相关文献运用强度折减法来考虑周围土体的各项参数变化对稳定性的影响，因此本文尝试通过这种方法来填补有关锚碇基础的影响因素方面内容。

首先考虑土体刚度的影响，为了便于比较，此处选取了3种情形下的稳定性分析，即（φ′=20°，和（φ′=30°，3种情形下的γsoilH保持不变。根据《土力学手册》中土体弹性模量的典型值范围来改变土体弹性模量并得到相应的关系曲线，见图7。

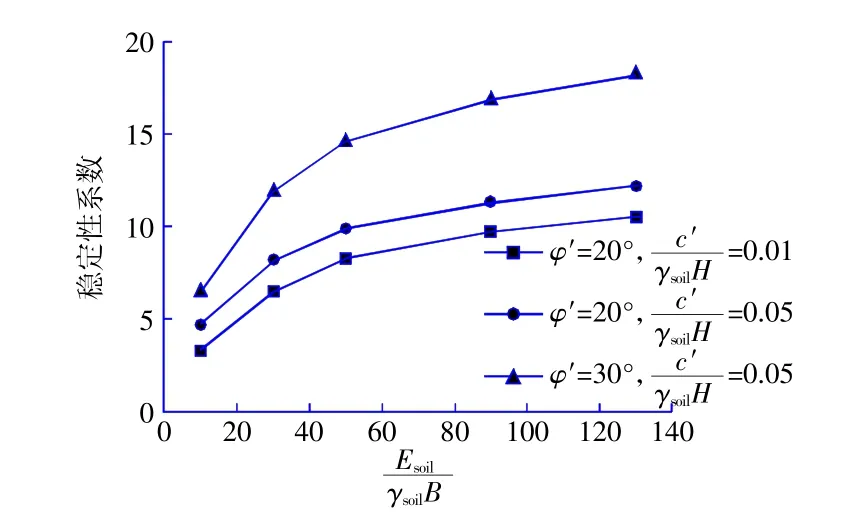
图7 稳定性系数与土体刚度比的关系曲线图Fig.7 Relationship curve between stability coefficient and soil stiffness ratio

为了便于比较，这里采用无量纲化参量来进行分析，图中给出了稳定性系数（亦称安全系数）与无量纲化刚度比的关系，从图中可知，稳定性系数随着的增大而增大，且呈非线性关系。当刚度比较小时其对稳定性的影响较大，随着刚度比增大影响逐渐减小。这是由于锚碇基底与前侧的土体随着锚碇自身的旋转而受到挤压，土体越来越密实，抵抗作用就越强；锚碇周围土体越密实，其刚度就越大，安全系数就越大。其次，相比于黏聚力来说，内摩擦角对稳定性的影响较大。总之，具有较大刚度的土体更能减小锚碇基础的旋转，同时锚碇基础会更加稳定。

其次考虑土体抗剪强度对稳定性的影响，这里通过改变内摩擦角φ′和无量纲化强度比来分析锚碇基础的稳定性。图8给出了3种情形下稳定性系数FS与无量纲化强度比的关系曲线，其中只改变黏聚力的范围，上述的3种情形分别为和其中γsoilB为常量。从图中可以看出稳定性系数FS随无量纲化强度比几乎呈线性增大的趋势。此外，内摩擦角与刚度相比，内摩擦角对稳定性的影响要更显著。

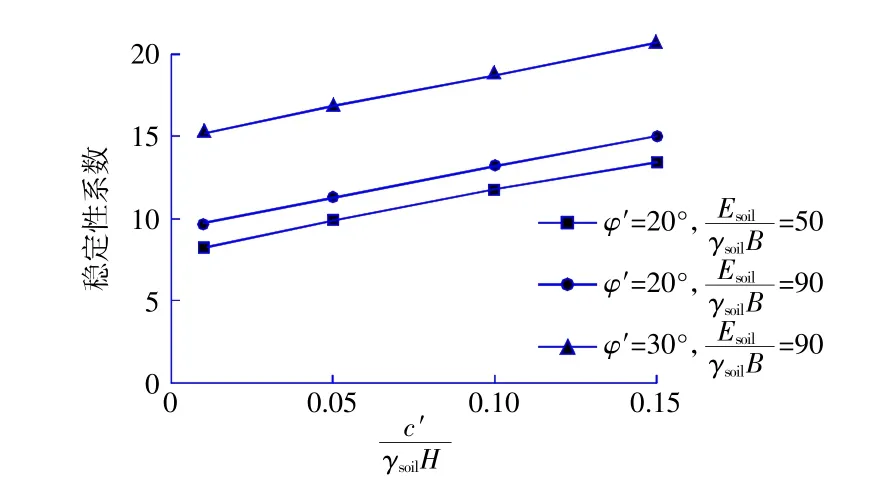
图8 稳定性系数与土体强度比的关系曲线图Fig.8 Relationship curve between stability coefficient and soil strength ratio

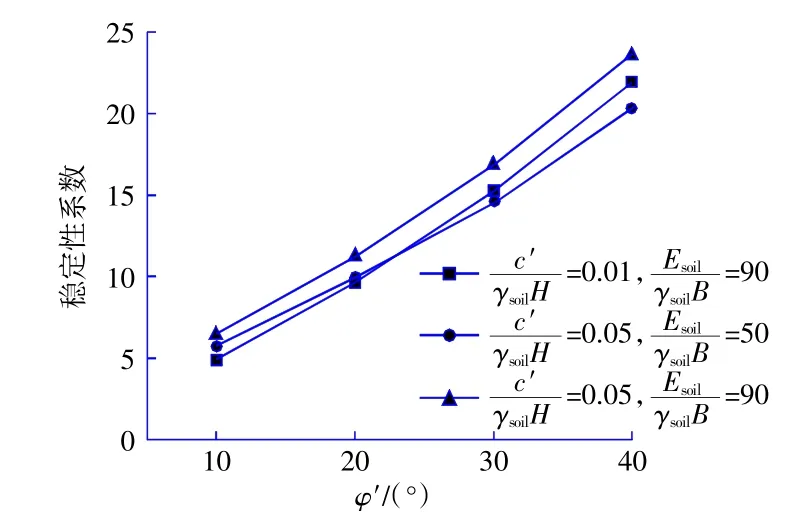
图9稳定性系数与土体内摩擦角的关系曲线图Fig.9 Relationship curve between stability coefficient and internal friction angle of soil

图9 的结果表明稳定性系数与内摩擦角φ′也近似呈线性关系，且稳定性系数随着内摩擦角φ′的增大而增大，土体的刚度与黏聚力对于稳定性的影响幅度相近。

5 结语

本文基于缩尺试验与有限元模拟进行锚碇基础的稳定性分析，并提出基于强度折减法的三维稳定性评估方法，得出以下结论：

1）重力式锚碇结构的倾覆旋转点并不在基底的脚趾处，而是在锚碇基础的底部，且基底前侧土体提供一定范围的抗力；当重力式锚碇基础处于极限平衡状态时，失效面穿越重力式结构底部的弧形区域。

2）三维稳定性系数FS随着土体弹性模量、内摩擦角和黏聚力的增大而增大。其中三维稳定性系数与土体弹性模量呈非线性关系，当刚度比较小时其对稳定性的影响较大，随着刚度比增大影响逐渐减小；

3）相比于黏聚力来说，内摩擦角对稳定性的影响较大；稳定性系数FS与周围土体的黏聚力几乎呈线性关系，与刚度相比来说，内摩擦角对稳定性的影响要更显著。

4）稳定性系数FS与内摩擦角也近似呈线性关系，且稳定性系数随着内摩擦角的增大而增大，土体的刚度与黏聚力对于稳定性的影响幅度相近。