空天飞行器星敏感器安装误差在线标定方法

安竞轲，熊 智，王 融，康 骏，张新睿，刘建业

(南京航空航天大学自动化学院，南京 211106)

0 引言

空天飞行器因其空地往返和可重复利用的特性而具有重要的战略意义。空天飞行器导航关键技术是实现其智能自主控制的核心技术，星敏感器作为空天飞行器组合导航系统中的传感器之一，通过观测恒星矢量解算载体姿态，由于其独有的隐蔽性和自主性，已经广泛地应用于卫星、飞船等在轨航天器中，对空天飞行器发射段和入轨段的自主导航具有重要作用。星敏感器自身输出的姿态精度可以达到角秒级，与惯性导航传感器组合能够有效抑制惯导姿态发散。但星敏感器的安装误差作为决定天文导航精度的主要因素之一，限制了空天飞行器一体化安装的惯性/天文组合导航系统的定姿和定位性能。

目前，星敏感器安装误差的标定与校正主要在起飞前地面上完成，文献[3]和文献[4]给出了利用星模拟器和方位基准相互配合对星敏安装误差进行标定的方法;文献[5]提出了星敏安装误差的三位置地面标定方法，以上方法均能精确地标定出星敏安装误差。但是，空天飞行器执行一次任务往往长达几百天，历经发射、在轨和再入3个任务阶段。一体化的惯性/天文导航系统中，星敏感器固联在载体上，由于发射过程中的振动、冲击、温度剧变等因素影响，以及随着长时间累积的安装角漂移，会使星敏感器发生角位移，导致其安装误差角可能达到角分级。因此，需要在载体起飞后，对星敏安装误差进行在线标定与实时校正，最大程度地隔离掉安装误差对组合导航系统的影响，保证组合导航系统输出的精度和可靠性。

文献[8]和文献[9]都提出了一种基于卡尔曼滤波的星敏安装误差快速标定方法，观测量为惯性/天文姿态信息，能够快速地标定出星敏安装误差；文献[10]基于星矢量观测利用卡尔曼滤波对星敏安装误差进行了标定，并分析了大、小视场下不同的标定效果；文献[11]提出了一种基于最小二乘法的星敏安装误差在线估计方法，利用估计残差统计特征量验证了算法的有效性;文献[12]提出了一种基于粒子群寻优的高精度星敏感器在轨标定方法，这种方法不依赖陀螺信息，提高了数据的准确性。

本文提出了一种基于恒星矢量观测的星敏安装误差在线标定与校正方法，将惯导姿态误差角与星敏安装误差角关联，将星光观测量与姿态、位置误差关联,并建立了系统状态与量测模型，通过卡尔曼滤波实现了对星敏安装误差角的在线标定与校正，并通过仿真验证了算法的有效性。

1 动态标定总体方案

星敏感器安装误差在线动态标定的总体方案设计如图1所示。本文选用大视场星敏感器和捷联惯导系统，首先建立包含惯导传统误差和星敏安装误差在内的卡尔曼滤波器状态方程，量测值由根据惯导系统输出信息计算出的相对于计算地理坐标系下的高度角和方位角的差值与星敏感器直接观测到的高度角和方位角构成。通过卡尔曼滤波算法对星敏安装误差进行实时估计，从而降低组合导航系统误差。

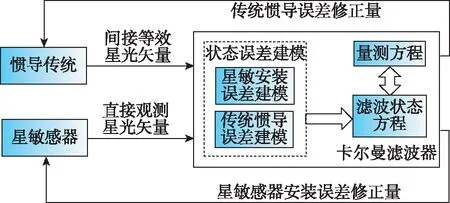
图1 方案框架图Fig.1 Scheme frame diagram

2 动态标定惯性、天文安装误差模型

2.1 星敏感器与捷联惯导系统安装误差角定义

由于空天飞行器高动态、长航时的运动特性，任务过程中的振动、冲击和温度变化均会引起星敏感器安装位置的偏移，同时随着时间累积，安装位置也会发生一定程度的缓慢漂移。综合以上情况，可将星敏感器的安装误差归纳为两种类型，如图2所示，一种是位移误差，一种是角度误差。由于空天飞行器中星敏感器主要起定姿功能，并忽略小位移引起的杆臂效应的变化，可以认为在飞行过程中只有沿着3个轴向的安装角度误差会对导航输出产生影响，针对安装角度误差，使用以下建模方法。

(a)位移误差

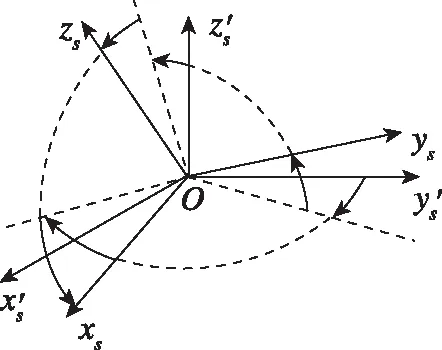
(b)角度误差

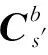
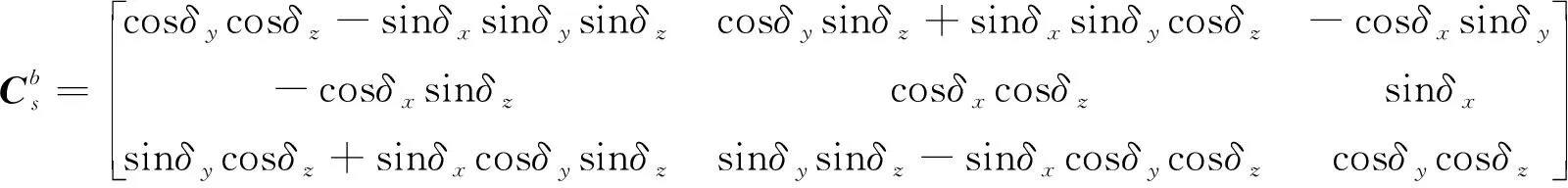
(1)

经过小角度近似得

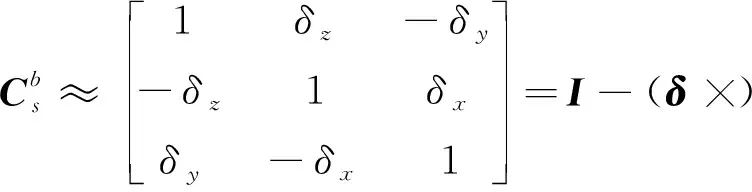
其中，×是的反对称矩阵

2.2 基于星矢量量测的观测方程

恒星观测矢量与天文导航观测角度的定义如图3所示。在坐标系-中，轴所在平面绕轴反向旋转角度定义为天文观测方位角，旋转后的中间坐标系定义为-；轴绕轴旋转角度定义为天文观测高度角，旋转后坐标系定义为-，旋转后轴即为星敏感器的光轴。在参考坐标系下,由天文观测角表示的星矢量为

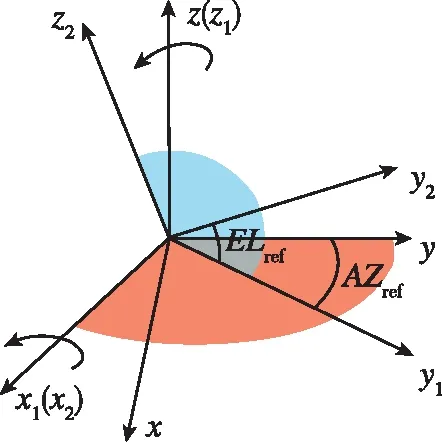
图3 天文观测角度定义Fig.3 Astronomical observation angle definition

=[sincoscoscossin]

(2)

式中，为单位星矢量；在参考坐标系下，为天文观测方位角，为天文观测高度角。

2.3 天文观测角与星敏安装误差角关系推导

将等效惯性平台坐标系下的星光矢量记为

=

[sincoscoscossin]

(3)

表示真实地理坐标系下观测到的星光矢量

=[sincoscoscossin]

(4)

假设相较于真实地理坐标系下的星光矢量存在着由星惯安装误差角导致的误差，即

=+Δ,=+Δ

(5)

将惯导平台误差角记为=[]，则从坐标系到坐标系的转换矩阵为

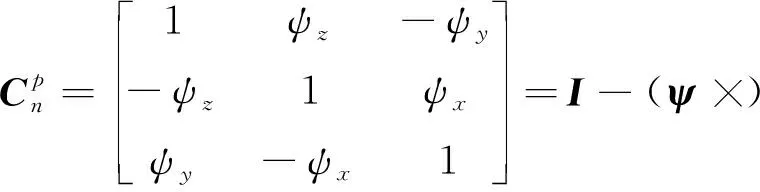
(6)

其中，×是的反对称矩阵。

同时，星敏感器坐标系下因安装误差角引起的惯导平台误差角有如下转换方式

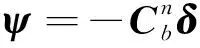
(7)

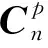
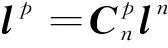
(8)

将式(3)、式(4)、式(5)和式(6)的值代入式(8)后得到

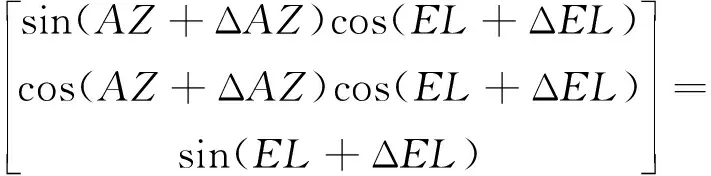
(9)

例，计算得到方位角误差Δ为-9.1″，高度角误差Δ为10.8″，证明了角分级的安装误差引起的方位角和高度角误差往往在角秒级水平，进而可对其进行小角度近似并忽略高次项误差，得到如下假设

(10)

根据以上假设，由式(9)可以得到天文观测角误差和平台误差角的关系

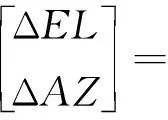
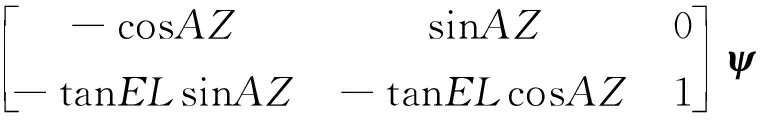
(11)

综合式(7)和式(11)可得

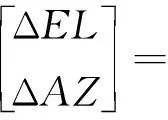
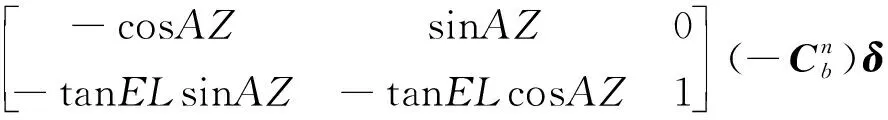
(12)

3 星敏感器安装误差标定方法

3.1 系统方程

利用线性卡尔曼滤波器进行组合，系统的状态方程和量测方程为

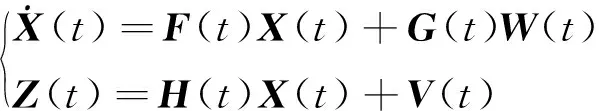
(13)

式中，()为卡尔曼滤波状态变量；()为卡尔曼滤波系统矩阵；()为状态变量噪声矩阵；()为卡尔曼滤波观测量；()为卡尔曼滤波观测矩阵；()为观测噪声。

(1)卡尔曼滤波状态方程

常规的卡尔曼滤波状态模型通常选用惯导系统的输出参数误差，分别为3个数学平台误差角(,,)、3个速度误差(δ,δ,δ)和3个位置误差(δ,δ,δ)；参考文献[16]中将惯性测量单元(Inertial Measurement Unit, IMU)的随机漂移误差(,,,,,,,,)这9个误差量作为陀螺仪和加速度计的误差量。基于第2节动态标定星敏安装误差模型，在已有滤波模型的基础上增加3个星敏安装误差(,,)，共21个参数作为系统的状态量，即

=[δδδδδ

δ

]

结合第2节星敏感器安装误差角与惯导数学平台误差角的转换关系，建立状态空间表达式

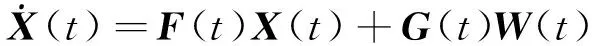
对应的系统矩阵()为

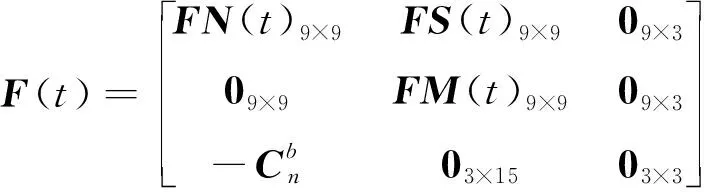
(14)

式中，()为基本导航参数变换矩阵；()为基本导航参数和惯导随机误差参数变换矩阵；()为IMU误差之间的关系矩阵。

3.2 量测方程

参考文献[17]可知，计算地理坐标系(系)与当地地理坐标系(系)之间考虑有小角度经纬度位置偏差δ、δ时，天文观测角误差与经纬度误差有如下关系

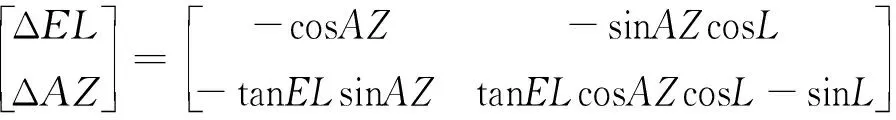
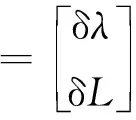
(15)

结合式(11)和式(12)有以下系统量测方程

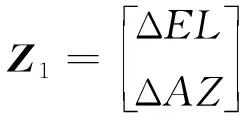
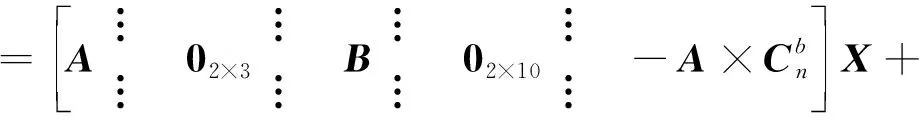
(16)

其中

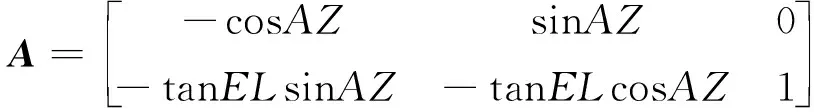
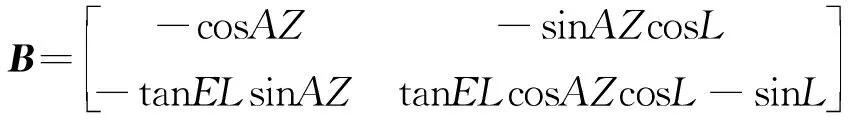
(17)

Δ=-, Δ=-

(18)

Δ、Δ分别为惯性输出信息等效后的天文观测角与星敏直接观测到的观测角之差；、分别为星敏感器观测输出的高度角和方位角的观测误差。通过以上建模方法，在保证了原有惯性/天文组合导航系统不受影响的前提下，增加了对安装误差的实时估计，并使得安装误差对组合导航系统的影响能够被及时消除。同时系统状态量的维数仅由18维增长到21维，仿真验证表明，单次卡尔曼滤波计算时间增长到了原来的1.36倍左右，并未过多地引起计算成本的增加。

式(16)为单星观测条件下的量测方程，当能观测到不止1颗导航星时，可以将式(16)进行扩展，即实现基于多星观测的量测方程，进一步提高安装误差估计精度。以2颗导航星为例，在双星观测条件下的量测方程为

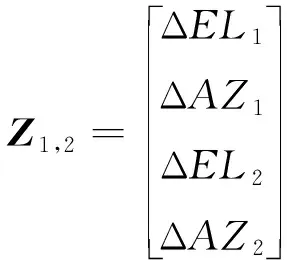
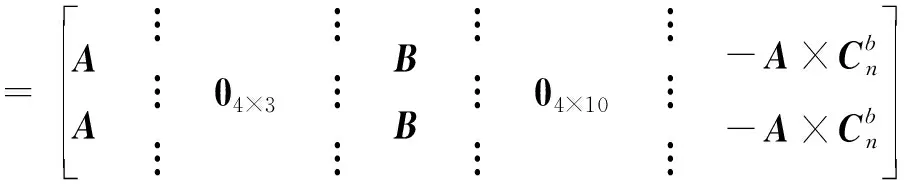
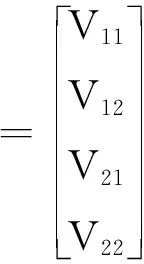
(19)

式中，、、、分别对应2组高度角和方位角的观测误差。

4 基于可观测性分析的误差标定飞行器航迹设计

系统可观测性分析方法包括基于奇异值分解的可观测性分析法和基于特征值的特征向量分析法，文献[20]对两种方法的原理和特点进行了详细分析，文献[21]针对星敏安装误差的估计与飞行器机动方式的关系进行了分析。本文采用奇异值分解的可观测性分析方法，通过产生不同的航迹飞行模式，对星敏安装误差在线辨识的可观测度进行了详细分析，并模拟了三种典型的转动机动方式，如表1所示。

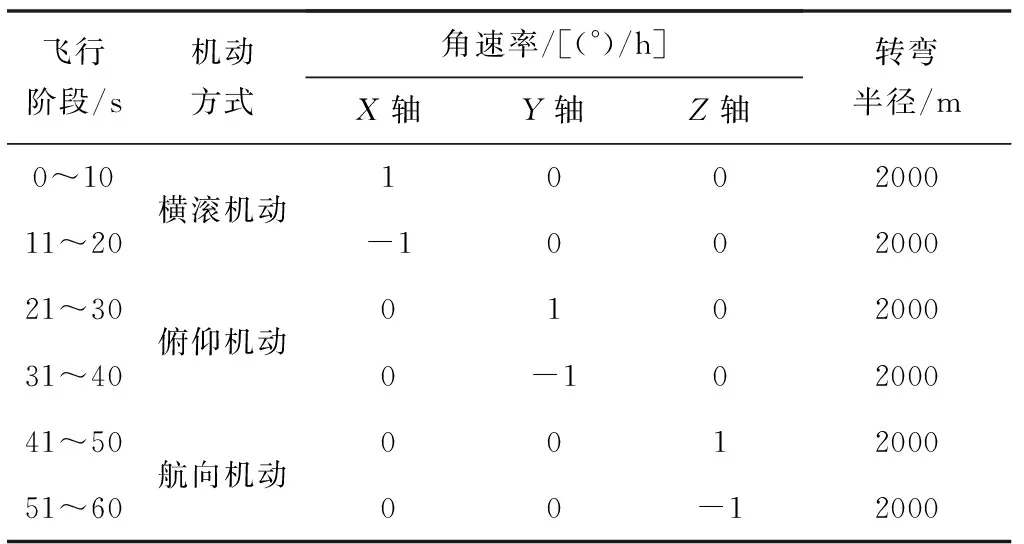
表1 转动机动方式

绘制不同机动方式下星敏安装误差对应的奇异值直方图,如图4所示。

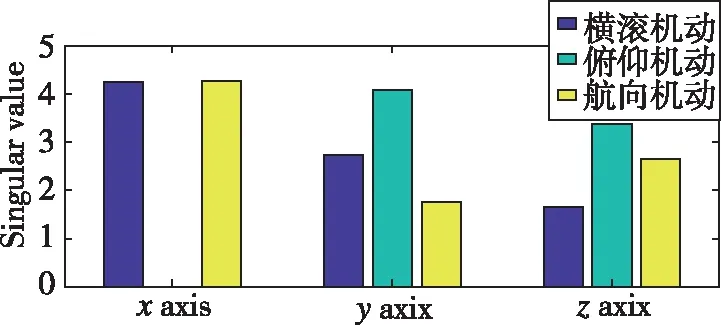
图4 星敏安装误差角对应的奇异值Fig.4 Singular value corresponding to star sensor installation error angle

从图4中可以看出，沿着机体系轴的安装误差在做横滚机动和航向机动时奇异值较大；俯仰机动对沿着轴的安装误差激励效果比较好;轴的安装误差在做俯仰机动时有比较好的可观测性。

通过图4所示的可观测性分析结果可以看出，仅通过机体的横滚和俯仰机动即可实现沿着机体系3个方向的星敏感器安装误差的较好激励，从而对其进行在线标定。基于空天飞行器跨空天的飞行模式和大动态长航时的任务特性，设计了图5所示的航迹规划方案，航迹总时间为1800s，其中前400s为标定阶段，包含了载体0～90s的横滚机动和200～290s的俯仰机动，使得星敏的安装误差具有比较好的可观测性，从而达到实时估计的目的；400～1800s为导航阶段，包含了3个轴向的线运动和角运动，对误差校正的有效性进行了验证。载体初始位置为东经118°，北纬32°，高度100km，初始北向速度100m/s，初始北向和天向速度为0，初始姿态角均为0。

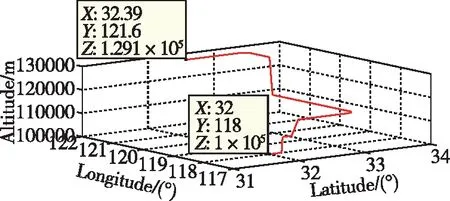
图5 航迹方案Fig.5 Track plan

5 仿真验证与结果分析

利用第4节中的航迹对标定方案进行仿真验证，该标定方案依赖高精度的天文观测水平基准，水平基准误差会导致星光矢量观测的偏移，如图6所示。同时，惯性/天文组合导航系统的水平基准精度由惯导姿态输出精度决定，本文通过四种仿真参数配置方案，以3颗观星条件为例，分析了不同惯导精度条件下的水平基准偏移和星敏安装误差标定结果，如表2所示，陀螺噪声包括白噪声和一阶马尔可夫过程模拟的有色噪声，星敏感器观测噪声为白噪声,其中水平基准精度通过惯导姿态误差角体现。

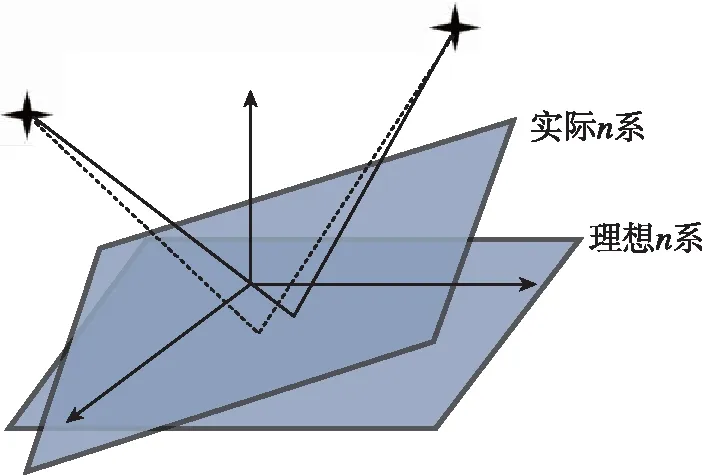
图6 天文观测水平基准误差示意图Fig.6 Astronomical observation level reference error

将不同条件下的安装误差标定结果与表2中设定的安装误差参数进行对比分析，结果如图7和表3、表4所示。

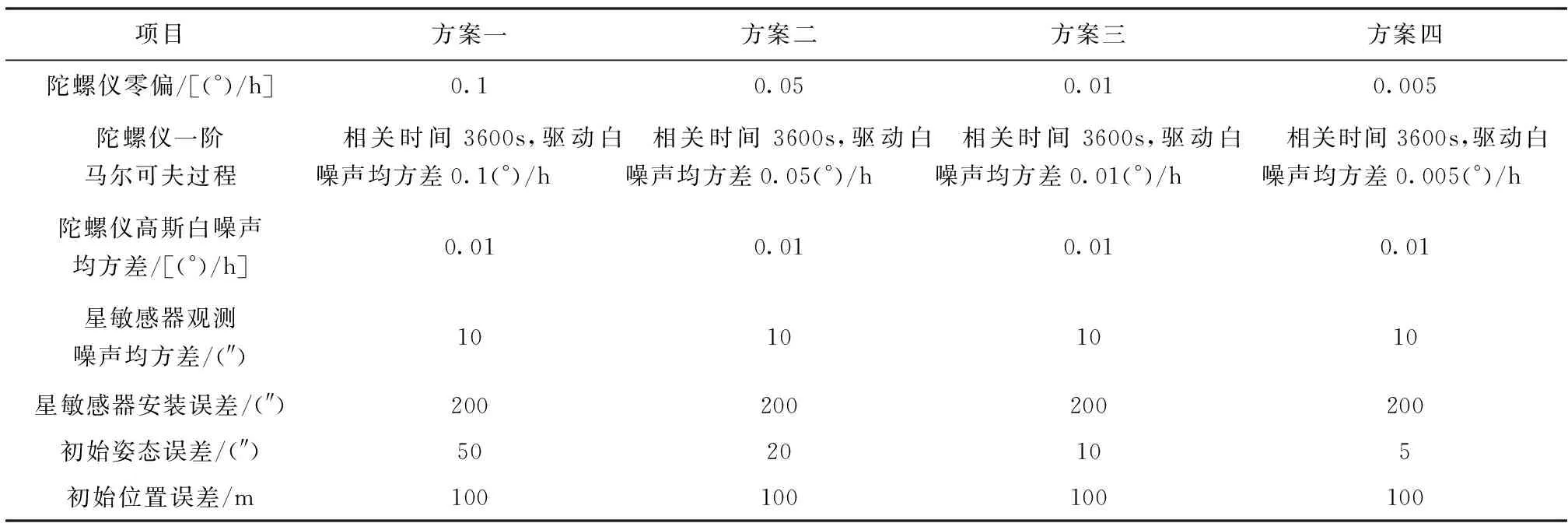
表2 系统误差参数

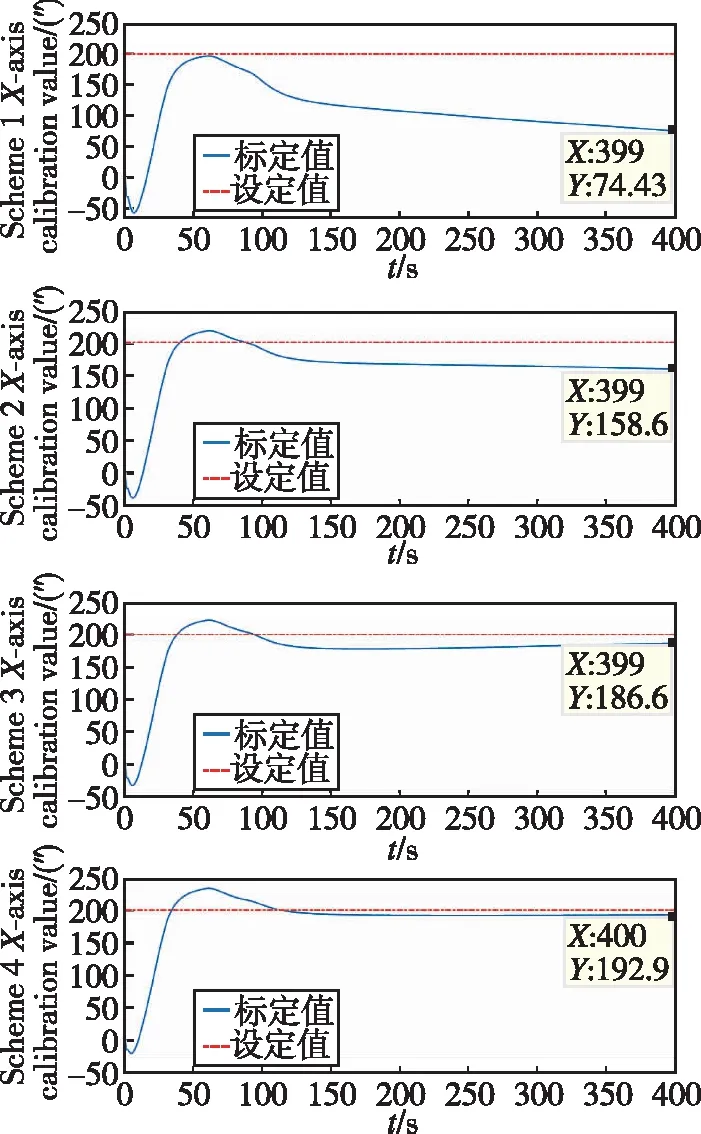
(a) x轴安装误差标定曲线

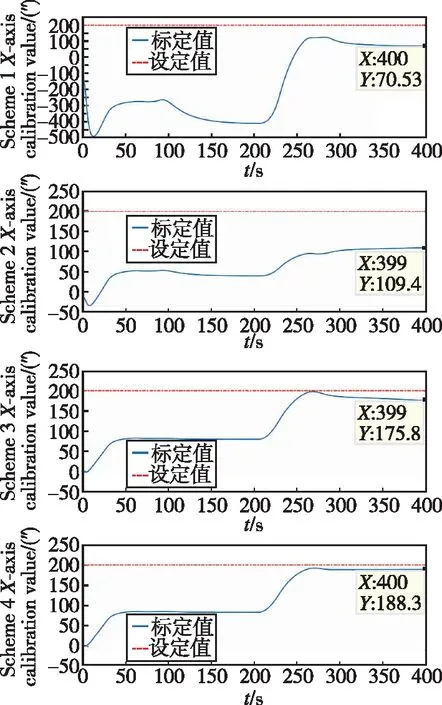
(b) y轴安装误差标定曲线

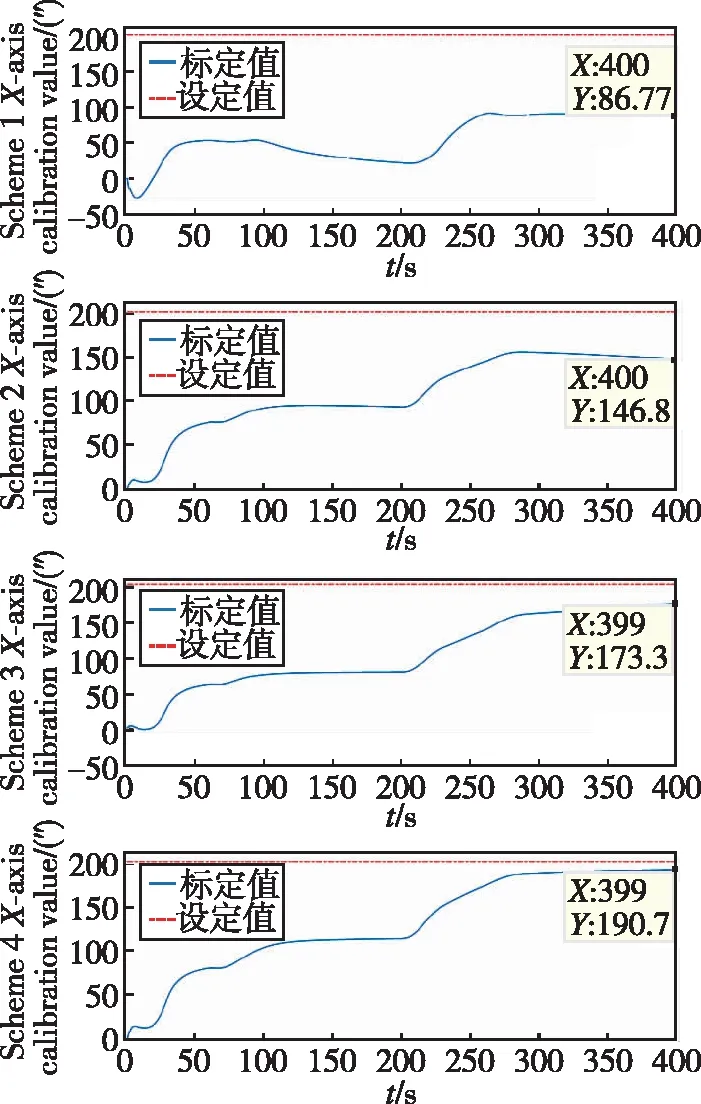
(c) z轴安装误差标定曲线图7 四种条件下星敏安装误差标定曲线Fig.7 Star sensor installation error calibration curve under four conditions

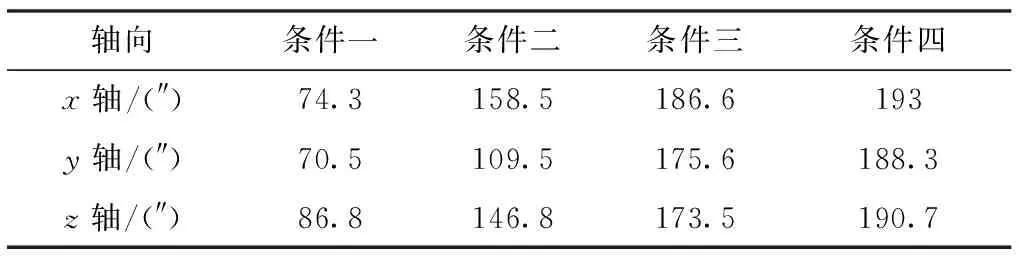
表3 四种条件下星敏安装误差标定结果

表4 四种条件下惯导姿态误差值

通过图7和表3、表4的结果可以看出，不同精度等级的惯导系统将引起不同精度等级的姿态输出，同时决定了不同星敏感器观测的水平基准精度，进而影响星敏感器安装误差的估计精度。从方案一和方案二的仿真结果可以看出，精度过低的惯导系统将无法实现对星敏安装误差的有效标定；条件三和条件四的标定结果能达到预设误差85%以上，其中轴能达到90%以上；另外，在横滚机动的0～90s内，轴方向已实现大部分预设安装误差值的估计，在120s后曲线趋于稳定；对于发生横滚机动的200～290s内，轴和轴方向也基本实现了预设安装误差值的估计，并在300s后开始趋于稳定，证明了该算法的收敛速度较快，能够满足一定的实时性要求。因此，在保证一定惯导精度的前提下，利用所设计的动态参数辨识方案能够实现对星敏安装误差的有效在线标定。

以方案三惯导精度为例，利用在线安装误差标定值对星敏感器进行安装误差反馈补偿，校正前后的惯性/天文组合导航系统误差对比如图8和表5所示。

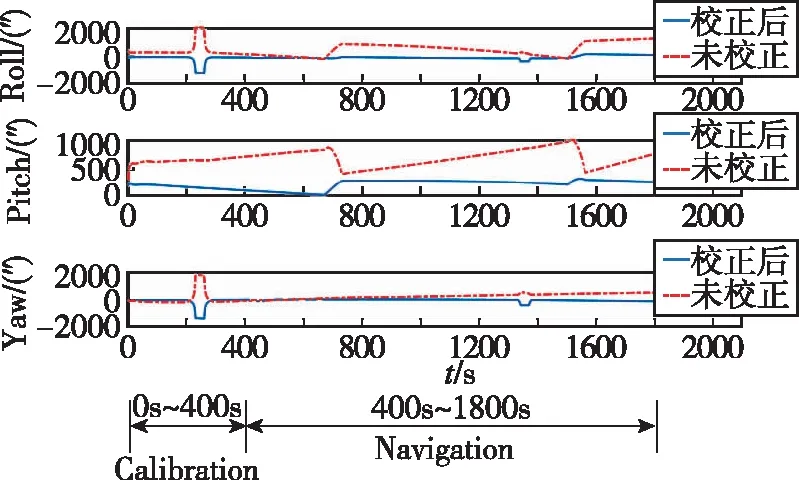
(a) Attitude error

(b) Position error

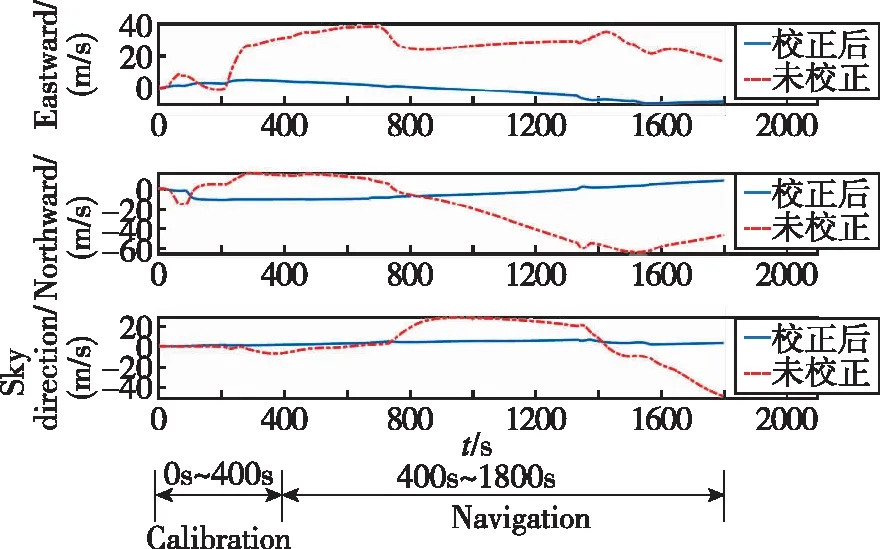
(c) Velocity error图8 未校正与校正后组合导航系统输出误差对比Fig.8 Comparison of output errors of uncorrected and corrected integrated navigation systems

表5 组合导航系统的最终误差值

由图8和表5可以看出，采用本文设计的在线标定校正算法的惯性/天文组合导航系统的定姿、定位精度远高于未校正的惯性/天文组合导航精度，姿态、位置和速度误差均下降了1个量级，精度提高了10倍，有效减少了星敏安装误差对组合导航系统性能的影响，能够满足高精度星敏感器补偿惯导系统误差的要求。

6 结论

本文建立了基于高度角和方位角观测的惯性/天文组合导航的卡尔曼滤波模型，通过模型可以看出，惯导的数学平台误差角与星敏感器的安装误差角之间存在着耦合关系，建立了通过观测量估计星敏感器安装误差角的滤波模型。

本文设计了星敏安装误差动态标定方案，基于构建的误差标定模型,利用卡尔曼滤波器对星敏安装误差进行实时标定。仿真结果显示，该方案能够准确且快速地对3个轴向上的安装误差进行实时估计，校正后组合导航输出精度得到了大幅提高，证明了本文提出的星敏安装误差实时校正算法能够明显地提高惯性/天文组合导航系统输出结果精度。

在理论分析之外，依然需要结合实际惯导和星敏感器实测数据对所设计的方案算法进行实验验证分析，从而实现其工程价值。