在深度学习视角下的单元复习专题教学
张宗玲

复习,要以学生的深度学习为出发点,注重知识之间横向和纵向的联系,才能使得数学知识不是碎片式存在于学生的知识结构系统中。深度学习倡导的是单元教学,强调的是知识整合。它是由知识面的宽度、知识本质的深度、数学思想方法的高度三个维度构成。从三个维度去关注学生学习数学的过程不能只是一个方向、线性的深度变化过程,需要关注三个维度的发展。下面就以圆的复习专题为例,谈谈专题单元复习。
一、内容
本复习内容为圆的证明和计算与旋转中的隐圆问题。
圆是“图形与几何”领域的核心内容之一,它是一种特殊的曲线图形,是在直线图形有关性质的基础上发展的基本图形之一,也是进一步学习数学的重要基础。“圆”是各省市中考的必考内容,圆的证明与计算对学生的数学素养要求比较高,不仅要求学生对圆的知识掌握熟练,而且还要有一定的研究方法。图形在旋转中容易与圆的基本要素产生联系,有些问题需要分析出隐藏在问题中的圆,利用圆的知识解决旋转中的求解问题。这部分内容的复习对于学生推理能力、几何直观和抽象能力的发展是至关重要的,也是进行深度学习的很好内容。
二、复习板块设计
(一)第一个板块:关注知识面的宽度,强化联系,发展数学素养
第二轮复习,是基于学生对圆的基础知识已经掌握的基础上进行的课程单元复习教学。这种复习要以学生的思维提升为目标,从深度学习的角度出发,以学生知识面的宽度和数学思维的宽度为主线,采取一题多解的教学策略,旨在从不同的角度去思考同一道题,用不同的方法寻找知识的生长点,使知识之间构建纵横联系网,让学生的几何直观、逻辑推理、抽象能力得到发展。
1.原题呈现。
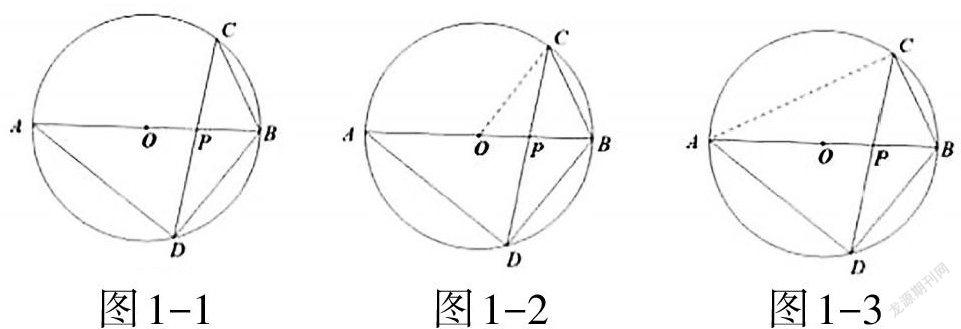
问题1:如图1-1,在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°,若∠APC=100°,求∠BAD和∠CDB的大小。
2.解法探究。
求∠BAD分析:由∠ABC=63°、∠APC=100°,可得∠C=∠APC-∠ABC=100°-63°=37°,再根据圆周角定理的推论可得∠BAD=∠C=37°。
求∠CDB分析:
方法1.如图1-1,由AB是直径可得∠ADB=90°,根据圆周角定理的推论可得∠ADC=∠ABC=63°,又因为∠CDB=∠ADB-∠ADC,所以∠CDB=27°。
方法2.如图1-2,连接OC,由题意可知OC=OB,根据等腰三角形的性质可得∠OBC=∠OCB=63°,从而可得∠COB=180°-∠OBC-∠OCB=54°,由圆周角定理可得∠CDB= ∠COB=27°。
方法3.如图1-3,连接AC,因为AB是直径,所以∠ACB=90°,所以∠CAB=90°-∠ABC=27°,由圆周角定理的推论可得∠CDB=∠CAB=27°。
3.说明。
所选题目为2020年天津市中考第21题第一问,题目的特点:题干的叙述简洁、明了,图形简单,但却涵盖了“圆”丰富的图形性质,以及八年级的三角形和等腰三角形的知识。
4.方法提炼。
圆的计算和证明通过不同的解法,使得弧、弦、角之间相互转化。如问题1,教学中引导学生由此及彼地进行联想、总结常添加的辅助线,构造直角三角形、等角、半角等,挖掘出内在的基本图形,培养学生思维的创新性。
(二)第二个板块:关注知识本质的深度,强化本质规律,发展数学素养
在各省市的中考中,以旋转为背景的题目层出不穷,在旋转问题中有这样的一类题目,通过旋转求线段最值的问题,学生感觉非常困难,之所以困难,是因为找不出解决问题的方法。由于方法的隐蔽性很强,对学生的直观想象要求比较高,在数学教学中,要善于利用几何图形的直观性去挖掘数学本质的规律——“隐圆”。通过这类问题的研究,可以提高学生对图形的性质理解和内化,加強学生对图形中各种元素之间的关系的认识。
1.原题呈现。
问题2:如图2-1,在平面直角坐标系中,O为原点,点A(-3,0),点B(0,[3]),以AB为一边作等边三角形ABC,点C在第二象限,将△AOB绕点B顺时针旋转得△A1O1B,点A,O旋转后的对应点为A1,O1。若点P为线段CO1的中点,求AP长的取值范围。
2.解法探究。
如图2-2,取CB的中点N,连接PN,AN。点O绕定点B进行旋转,BO为定长,则对应点O1在圆心为点B、半径为OB长的圆上运动,轨迹圆与BC相交于一点,即为点N,点P随着点O1位置的变化而变化,问题是点P的运动轨迹是什么?由于点P和点N都是中点,因此PN为三角形CO1B的中位线,O1B是定长,则PN也是定长,因此,动点P的轨迹是以点N为圆心,PN的长为半径的圆。
由题意,点A、N为固定点,则以点N为圆心,PN长为半径的圆是动点P形成的轨迹,所以当A,P,N三点共线时,AP取得最大值、最小值,即AN-PN≤AP≤AN+PN,即_____________。
3.说明。
此题是2020年天津市和平区三模第24题第3问,动点P的轨迹比较难想象,让学生明确求AP长的范围就是确定AP的最大值和最小值问题。
4.方法提炼。
利用圆的定义,找定点、寻定长,使得隐形圆现出。已知点A、N为定点,线段NP绕点N旋转,当点P在线段AN上时,如图,线段AP最短,当点P在线段AN的延长线上时,线段AP最长。
三、复习专题设计思考
1.单元复习专题紧扣“四条主线”。
教学中突出四条主线,并注重四条主线的和谐发展。一是突出知识面的宽度—强化内在联系(知识之间横向联系)—发展思维(一题多解)—形成方法(提升思想方法);二是突出知识本质的深度—强化本质规律(运动)—发展思维—形成方法;三是突出“显性知识(明“圆”)—隐性知识(隐圆)”的思维活动;四是突出教师“引导探究—解析(归纳、概括)—评价”的过程。
2.单元复习设计的反思。
在深度学习的视角下思考圆的复习专题,设计从静态圆到动态圆的学习过程。一题多解,给学生创设思维的空间,学生的思维活跃起来才会有新的惊喜,学会从复杂的图形中借助辅助线构造基本图形,运用圆的基本性质进行计算或证明,学生思维的灵活性与深刻性得以提升,知识面的宽度得到关注。让图形旋转起来,引导学生找准切入点,抓住关键点,分析出其中的隐圆,指导学生合理地借助圆的直观,将“数”转化为“形”的问题进行研究,使求解问题与圆的要素之间产生关联,抓住“变”与“不变”的核心,关注知识之间的逻辑关系,围绕“延伸点”,让学生在复杂图形的运动和变化中,提升学生数学思考的深度和广度,知识本质的深度得以体现。
3.复习专题更应注重思想方法的提升。
提升数学思想方法的高度是深度学习的第三个维度,初中学生还处于形象思维阶段,对于“静止状态”的图形基本性质的理解及运用还需“形象化”,对于“变换形态”图形的理解,要把数学学习的过程“直观化”“可视化”,这就需要借助几何直观来完成,从无“形”到有“形”,抽象能力是主导。以“形”的直观辅助对“数”的思考,以“数”的逻辑推理判断“形”的改变,直观离不开逻辑,逻辑离不开直观。因此,学会用图形进行思考、用图形进行想象,学会用图形的运动与变化的方式去认识和理解数学,是学习数学所具备的能力,也是复习专题要实现的目标。
(徐德明)

