多线性考尔德伦-赞格蒙(Calderon-Zyg mund)算子交换子在莫里(Morrey)空间上的端点估计

刘建明,黄时祥

(1．吉首大学 数学与统计学院,湖南 吉首 416000;2．上饶师范学院 数学与计算机科学学院,江西 上饶 334001)

1 引言及主要结论

众所周知,经典的奇异积分算子T是调和分析中的重要组成部分,其定义为:

其中核函数K(x)满足一定的消失性条件、尺寸条件和光滑性条件,具体内容读者可参见文献[1]。

1961年,约翰(John)等[2]在研究偏微分方程问题时引入了有界平均震荡函数空间BMO,其定义为:

设b∈BMO,由经典奇异积分算子T和函数b生成的交换子定义为:

奇异积分算子交换子是由考夫曼(Coif man)等[3]定义的,并且他们还得到了此交换子的Lp有界性,其中1＜p＜∞。但是,该交换子在p＝1时的弱有界性一直未得到很好解决。1995年,佩雷兹(Perez)[4]给出了一个反例说明了Tb不是弱 (1,1) 型,然后作者证明了此类交换子满足一种弱L(log)L型端点估计。

多线性Calderon-Zyg mund算子理论最早可追溯到20世纪70年代,由Coif man等[5]提出。2002年格拉法克斯(Graf akos)[6]研究了如下一类多线性Cal der on-Zyg mund算子,其定义为:

定义1．1[6]设(f1,f2,…,fm) ∈C0∞,K(x,y1,…,ym) 为(Rn)m+1中局部可积函数且(x,y1,…,ym) ∈(Rn×…×Rn){x＝y1＝…＝ym} ,记:

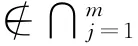
过去20年,众多数学工作者参与研究多线性Cal der on-Zyg mund算子理论,并且在研究过程中得到了许多有意义的结论,读者可参见文献[7-8]。

设(b1,…,bm) 且bi∈BMO,则由多线性Calderon-Zygmund算子T和生成的多线性Calderon-Zygmund算子交换子的定义如下:

多线性Cal der on-Zyg mund算子交换子最早是由Perez等人研究引入,具体工作可参见文献[9]。随后多线性交换子得到了众多数学工作者的关注,例如勒纳(Ler ner)等人[10]得到了多线Cal der on-Zyg mund算子交换子的弱L(log)L型加权端点估计。

1938年,Morrey[11]在研究二阶椭圆型偏微分方程解的局部性质时引进了经典Morrey空间,其定义为:

其中B(x,t)表示Rn中任意一个以x为中心,t为半径的球体,0≤λ＜n,1≤p＜∞。

类似地,弱型Morrey空间定义如下:

2016年,王(Wang)[12]定义了一类新型广义Morrey空间,并得到了奇异积分算子及其交换子在这类新型广义Morrey空间上的有界性。

为获得交换子的端点估计理论,我们先介绍关于奥尔里奇(Orlicz)空间的一些定义和结论,具体内容读者可参见文献[13]。

设φ(x) 是定义在 [0,∞) → [0,∞) 上的Young函数,满足φ(0)＝0、＝∞且φ(x) 在定义域内为连续的、凸的、递增的函数。

接下来我们介绍卢森堡(Luxemburg)范数的定义,对于一个函数f和方体Q,记:

称上式为f在方体Q上的Luxemburg范数,当φ≤φ＇时有‖f‖φ,Q≤‖f‖φ＇,Q。

对于任意杨(Young)函数φ,我们定义它的互补函数。如果Young 函数φ(t)＝t(1+log+t) ,则它的互补函数为(x) ≈ex。

接下来我们介绍广义赫尔德(Hol der)[14]不等式,记:

当φ(t)＝(1+l og+t) 时,令‖f‖φ,Q＝‖f‖LlogL,Q,‖f‖φ-,Q＝‖f‖expL,Q,(1)式也可表示为:

设b∈BMO(Rn) ,由约翰-尼伦伯格(John-Nirenber g)不等式我们不难得到:

(3)式的证明可参见文献[4]第169页。

结合(2)(3)式可得:

文献[12]中,Wang介绍了LlogL型的广义Morrey空间。在介绍该类型空间定义前,我们先介绍如下函数条件:

设0≤k＜1,θ(·) 是定义在 (0,∞) 上的非负增函数并且满足以下一类Dk条件:

其中C1＞0且不依赖于ξ、ξ'。LlogL型的广义Morrey空间定义如下:

显然当θ(B)＝就为LlogL型的经典Morrey空间,其定义为:

定义1．2 设B(x,t)表示Rn中任意一个以x为中心,t为半径的球体,0≤λ＜n

文献[12]中,Wang研究了奇异积分算子交换子在此类新型广义Morrey空间上的弱LlogL型端点估计。主要结果如下:

定理A[12]设b∈BMO(Rn) 、θ满足Dk条件,则对于任给的σ＞0和任意的B⊂Rn,存在一个不依赖于函数f、球体B、σ的常数C＞0,使得:

文献[10]中,Ler ner等人介绍了如下一类多线性极大函数M()(x) ,记:

其中(f1,…,fm) 、m∈Z+(m＞1) 且对所有包含x的球体B取上确界。

2021年,喻(Yu)等人[15]研究了由上述多线性极大函数生成的交换子,其定义如下:

定理B[15]设bi∈BMO(Rn) 、ω满足一类二倍条件既ω(2B) ≤C0ω(B) 、1＜C0＜2n,对任意β＞0和任意以x∈Rn为中心、t＞0为半径的球体B,使得:

其中Φ(t)＝t·(1+log+t) ,,常数C＞0且依赖于维数n。

其中0≤λ＜n,Φ(t)＝t·(1+log+t) ,‖bi‖BMO,常数C＞0且依赖于维数n。

受以上论文的启发,本文将研究多线性Calderon-Zyg mund算子交换子在Morrey空间Mp,λ上的弱LlogL型端点估计,本文主要结论如下:

定理1．1 设bi∈BMO(i＝1…m) ,0≤λ＜n对任意σ＞0和任意以x∈Rn为中心、t＞0为半径的球体B,存在一个不依赖于fi(i＝1…m)、球体B、σ的常数C＞0使得:

活性炭本身作为一种多孔状碳元素吸附物质，在刚刚出厂时应当是粗糙且不平整的，从显微镜下观察能够发现其表面呈现出凹凸不平和孔洞型结构[2]。一般情况下，活性炭内部的孔隙呈现出无序的状态，但总体而言其孔隙结构越复杂、比表面积越大，吸附能力也就越强，活性炭质量越高。一般情况下测试活性炭性能的方法可以采用压汞法或氮气吸附法。压汞法的主要原理为：取小块活性炭进行压汞分析，观察活性炭再生工艺前后比表面积的变化情况；而氮气吸附法的原理在于通过多分子吸附理论来分析活性炭孔隙吸附质量，一般情况下前者适用于孔隙较大的活性炭检测，后者适用于微米级活性炭检测。

其中φ(t)＝t( 1+log+t) 、‖bi‖BMO。

2 预备知识

引理2．1[16]设b∈BMO,则对于任意在Rn中的球体B有:

引理2．2[10]设∈BMOm,则存在一个依赖于‖b→‖BMO的常数C使得:

引理2．3[17]设,fj∈Lpj,∞其中0＜pj＜∞、1≤j≤k则有:

其中Lp,∞(Rn)＝＜∞} 。

3 主要结果的证明

所以I1≤C‖b1‖BMO。

因为

所以对I3可进行以下分解:

由运算可得:

结合t≤φ(t)＝t·１+log(+t) 和的定义可得:

又因为λ＜n,由级数收敛可得:

所以J1≤C‖b1‖BMO。

对J2进行以下分解:

由t≤φ(t)＝t·(1+log+t) 可得:

由(4)式可得:

又由(3)式可得:

对J4,由t≤φ(t)＝t· (1+log+t) 可得:

因为λ＜n,由级数收敛可得:

所以J4≤C‖b1‖BMO。

综上,I3＝J1+J2≤C‖b1‖BMO。

对I2而言,我们取α1＝α2＝α3＝0,α4＝…＝αm＝∞不失一般性,运用引理2．3可得:

结合文献[4]中奇异积分算子交换子弱L(l og)L型端点估计可得:

同理可得:

所以I2≤C‖b1‖BMO。

综合对I1,I2,I3的估计,并对所有球体B取上确界可得定理1．1证毕。