基于MATLAB的汽车悬架系统参数分析

2022-03-28 13:56李小伟高清冉

济源职业技术学院学报 2022年1期

李小伟，高清冉

(济源职业技术学院机电工程系，河南济源 459000)

汽车悬架系统的控制问题一直是自动控制技术研究的一个典型的问题，控制的主要目标是汽车在不同行驶道路环境下，获得较好的机动性、平稳性。悬架系统在汽车中的主要任务是将车身和车轮连接在一起，通过弹簧和阻尼元件在减震的同时传递力和力矩。车轮和车身由弹性元件连接在一起，弹性元件一般为弹簧，主要作用是在路面不平引起汽车颠簸时进行减震。悬架系统的动态性能决定了汽车行驶在不同地形道路上汽车的快速机动性和良好的舒适性[1]，因此，本文以单位阶跃信号作为激励模拟颠簸路面，建立动力学方程，借助于MATLAB计算机仿真技术，对悬架系统进行时域动态性能分析，通过仿真结果动态的分析比较，选择优化后的悬架系统参数。汽车悬架系统一般由弹性元件、阻尼器和导向机构(车轮)三部分组成，并支持车身、弹性元件连接车轮和车厢，实现减震、缓冲和导向的作用，改善乘坐感受。图1为汽车一个车轮的悬架系统(1/4悬架)物理模型[2]。

图1 悬架系统物理模型

一、悬架系统数学模型

(一)二阶系统模型

悬架系统连接的汽车一般有四个轮子，本文在进行分析时采用1/4车辆悬架物理模型来进行分析。这里我们选定模拟一个车轮而忽略其他车轮响应的单自由度系统，根据牛顿定律进行数学建模，建立动力学方程，最终其数学模型为一个二阶系统[3]：

(1)

其中f(t)是地面力，m是1/4车辆悬架物理模型的质量，b是阻尼器阻尼系数，k是弹性元件常数，y为从平衡位置开始的位移量。本次研究模型中不包含汽车轮子的质量和车胎的动态特性。由于许多厂商采用英制单位规定产品，故本例使用英制单位。若整个车的重量约为2000磅(lb)，汽车有四个轮子，本文采用的是1/4车辆悬架模型，因此总质量m=500 lb。

为了对颠簸道路状况下的方案进行评价，本文选用单位阶跃信号来表示颠簸路面的情况，将不同道路状态模拟成幅值为x0的地面阶跃输入[4]。

(2)

式(1)中的地面力用输入信号替代得：

(3)

二阶系统阶跃响应动态特性由特征方程根决定，对动力学方程进行Laplace变换得到其传递函数：

(4)

二阶系统的特征方程为：

ms2+bs+k=0

(5)

方程特征根就是系统的极点，即

(6)

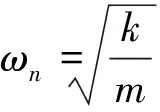
(二)汽车悬架系统模型的根

根据汽车悬架系统模型动力学方程之根的阻尼情况，对无阻尼、临界阻尼、欠阻尼和过阻尼四种情况进行讨论。

1.无阻尼系统

此时阻尼器的阻尼系数b=0，系统中没有阻尼，悬架系统模型简化质量-弹簧系统，对应的位移量输出为：

y(t)=Acosωnt+Bsinωnt

(7)

该输出是正弦和余弦叠加的等幅振荡。

2.临界阻尼系统

阻尼比ξ=1，阻尼系数b≠0，系统中存在阻尼，对应的位移量输出为：

y(t)=(A+Bt)e-ωnt

(8)

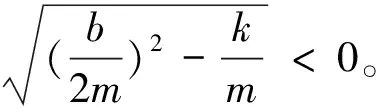
此时的阻尼系数：

(9)

同时求出非临界阻尼系统的阻尼比：

(10)

3.欠阻尼系统(0<ξ<1)

对应的位移量输出为：

y(t)=e-ξωnt(Acosωdt+Bsinωdt)

(11)

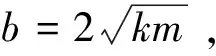
(12)

位移量输出与系统的阻尼比、振荡频率、位移量A和B有关[5]。

上述位移量输出中A和B都是由弹簧初始条件、位移和偏移量确定的常数。

二、悬架系统的参数分析优化

不同道路上悬架系统的减震效果及稳定性，是评价驾乘环境的动态性能指标的重要依据之一。动态性能在自动控制理论中常用的分析方法有两种：一是阶跃响应时域分析法，二是采用正弦输入的频域法进行分析[6]。本文采用单位阶跃响应时域分析法，在给出合适的弹簧常数k和阻尼系数b的基础上，对悬架系统的超调量、上升时间等表征快速性和稳定性的参数进行分析评价。

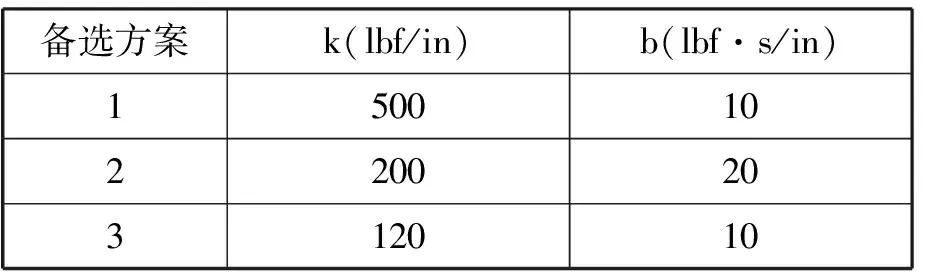
表1 备选方案表

表2 参数表

从阻尼比ξ看出，每个方案的ξ均小于1的值，因此三个备选方案都属于欠阻尼系统响应。二阶系统的应用在自动控制技术中颇为普遍，而且一些高阶系统在分析设计时，在一定条件下也会简化为二阶系统。随着计算机技术的发展，用计算机仿真技术对自动控制技术进行辅助设计变得屡见不鲜。本文采用MATLAB软件对悬架系统二阶系统进行分析。

标准的二阶系统传递函数为：

(13)

将三组备选方案的参数带入进行分析，并通过MATLAB编程绘制阶跃响应曲线，备选方案传递函数及MATLAB实现语句如表3所示[9]。