基于高频位置矫正法的永磁同步电机低速域抗扰动插值控制策略

张冰鑫，刘 侃，周世超，李 跃，屈阳华，耿扬策

(1.湖南大学 机械与运载工程学院，长沙 410082；2.火装驻长沙地区军代室，长沙 410205)

0 引 言

永磁同步电机(以下简称PMSM)具有功率密度大、起动速度快、过载能力强等优点，广泛应用于电动车、风力发电、牵引传动等场合[1]。在永磁电驱动系统中，转速环/位置环控制需要精确的转子位置信息，其一般从电机轴上的光电编码器或旋转编码器得到，而高分辨率的位置编码器价格昂贵，增加了驱动系统的硬件成本[2-3]。为降低成本，在保证驱动性能的前提下，采用低精度编码器是一个可行的思路。这种情形常见于牵引系统中，牵引系统采用霍尔位置传感器进行低速起动及控制。当系统在低速工况运行时，由于霍尔位置传感器的低分辨率特性，电机控制器在长达数十个采样周期内无法获得真实的转子位置，从而使转速环/位置环的控制性能受限[4-5]。采用插值算法来提高低精度编码器的分辨率是一种主流的解决方案，这种方案既不产生额外的成本，又可以有效提高转子位置精度。

近年来，涌现了许多插值控制方案，如平均速度法[6-9]、平均加速度法[10]、矢量观测器法[11-13]。文献[6]提出了平均速度法，利用前一个离散位置区间的平均速度估算当前区间的位置，但需要额外的硬件实现算法。文献[7]在平均速度法的基础上，将插值算法变更为软件实现，降低了操作难度和成本。此外，去除电流传感器可以进一步降低成本，且利用q轴参考电流补偿位置估计误差，可改善平均速度法的起动问题[8]。负载变化影响平均速度法的估算精度[9]，在负载变化大的应用中，需要进行负载补偿。文献[10]提出了平均加速度法,利用前两个离散位置区间计算出的平均加速度估算当前区间的转子位置，实现在加减速过程中对位置进行有效估计。文献[11]借鉴无传感器技术中的旋转矢量思想，提出了位置矢量观测器法。文献[12]提出了一种改进的谐波解耦策略，使得位置观测具有零滞后特性，因观测器用到了系统机械模型，故算法易受到系统惯量、负载变化等因素的影响。另外，通过补偿霍尔传感器的偏置效应，可提高霍尔传感器的瞬态性能[13]。

文献[14]提出了一种基于观测器法的累积增量插值控制算法，但外界施加的持续扰动严重影响位置观测精度。针对该插值算法抗外界扰动能力差的问题，本文提出了一种基于高频位置矫正的插值算法，在750 W伺服控制系统验证了该控制策略的有效性。

1 插值算法原理

依据电机工况，观测转子位置信息的算法可划分为两大类：适用于零低速域的信号注入法和适用于中高速域的模型法。因本文的算法需与文献[14]中算法形成对比，考虑对比的公平性，故本文采用模型法中的降阶扩展卡尔曼滤波算法获取与位置关联的反电动势信息，滤波后的反电动势经过锁相环处理，获取实时的位置信息。在此基础上，利用插值算法估计电机转子的实时位置信息。

1.1 转子位置观测器

本文采用降阶扩展卡尔曼滤波算法获取反电动势信息，反电动势信息中存在与位置相关的信息。由于转速降低，观测出的反电动势无法直接用于位置观测，本文采用自适应滤波算法，消除反电动势中的谐波干扰。

忽略涡流和磁滞损耗等，在id=0控制下，PMSM在静止αβ轴系的电压方程可简化如下：

(1)

式中：uα和uβ为α，β轴电压；R为电机定子绕组；iα和iβ为α，β轴电流；Lq为q轴电感；ω为电气角速度；ψf为永磁体磁链；θ为电气转子位置角。

含有反电动势的PMSM电流状态方程表示如下[15-16]：

将式(3)整理成典型的系统状态方程：

通常来说，运行电机的反电动势无法直接量测，通过后向一阶差分将电流状态式(2)离散化，获得下式：

zk=

(5)

式中：eα(k-1)，eβ(k-1)为上一时刻的α，β轴的反电势；uα(k-1)，uβ(k-1)为上一时刻的α，β轴电压；iα(k-1)，iβ(k-1)和iα(k)，iβ(k)为上一时刻和当前时刻的α，β轴电流。因处理器的采样时间极短，相邻采样时刻电气量近似不变，故离散计算过程中可用上一时刻的电气信息参与当前时刻的控制运算。

降阶扩展卡尔曼滤波算法实现步骤如下：

先验状态预测：

计算先验协方差矩阵：

计算卡尔曼增益：

修正先验预测值：

更新协方差矩阵：

式中：x是系统状态变量；“^”表示估计量；P是协方差矩阵；“-”表示上一时刻的(先验)协方差矩阵；无‘-’表示当前时刻的协方差矩阵；Q表示系统精确建模引入的噪声项，R表示量测引入的噪声项，两个噪声项的统计特性依据假设，均服从正态分布，Kk表示卡尔曼增益，用于修正预测值；I表示单位矩阵；A表示系统转移矩阵，A=I+TsF，Ts是控制系统的采样时间，F表示雅可比矩阵；H表示测量矩阵。雅可比矩阵和测量矩阵的表达式：

在算法实现过程中，P0与x0需赋初值。

1.2 自适应滤波策略

在低速工况下，降阶卡尔曼滤波算法观测的反电动势含有噪声，为了降低反电动势谐波，需要对其进行滤波处理。一般的滤波思路是采用低通滤波器，消除高频噪声，但过低的滤波器截止频率会引入较大的相位滞后，严重降低观测器的动态观测性能。本文采用自适应滤波策略消除谐波干扰，同时，该策略可以有效改善相位滞后现象。反电动势滤波示意图如图1所示[17-18]。

图1 反电势滤波器示意图

由上文推导可知，反电动势导数满足下式：

本文的自适应滤波实现原理如下[14]：

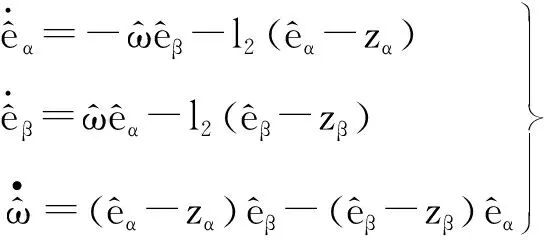
(12)

1.3 高频位置矫正策略

本文采用高频注入改善插值算法对外界持续扰动的鲁棒性能，当电机注入高频信号时，电机高频模型[19]：

高频位置算法在虚拟d轴注入高频信号，在静止轴系提取高频响应电流信号，所得高频电流经符号化处理后，其表达式：

本文采用无滤波器分离技术获取高频响应电流信号[20]，进而通过锁相环技术获取转子的实时位置信息。图2是锁相环的原理框图。

图2 锁相环结构简图

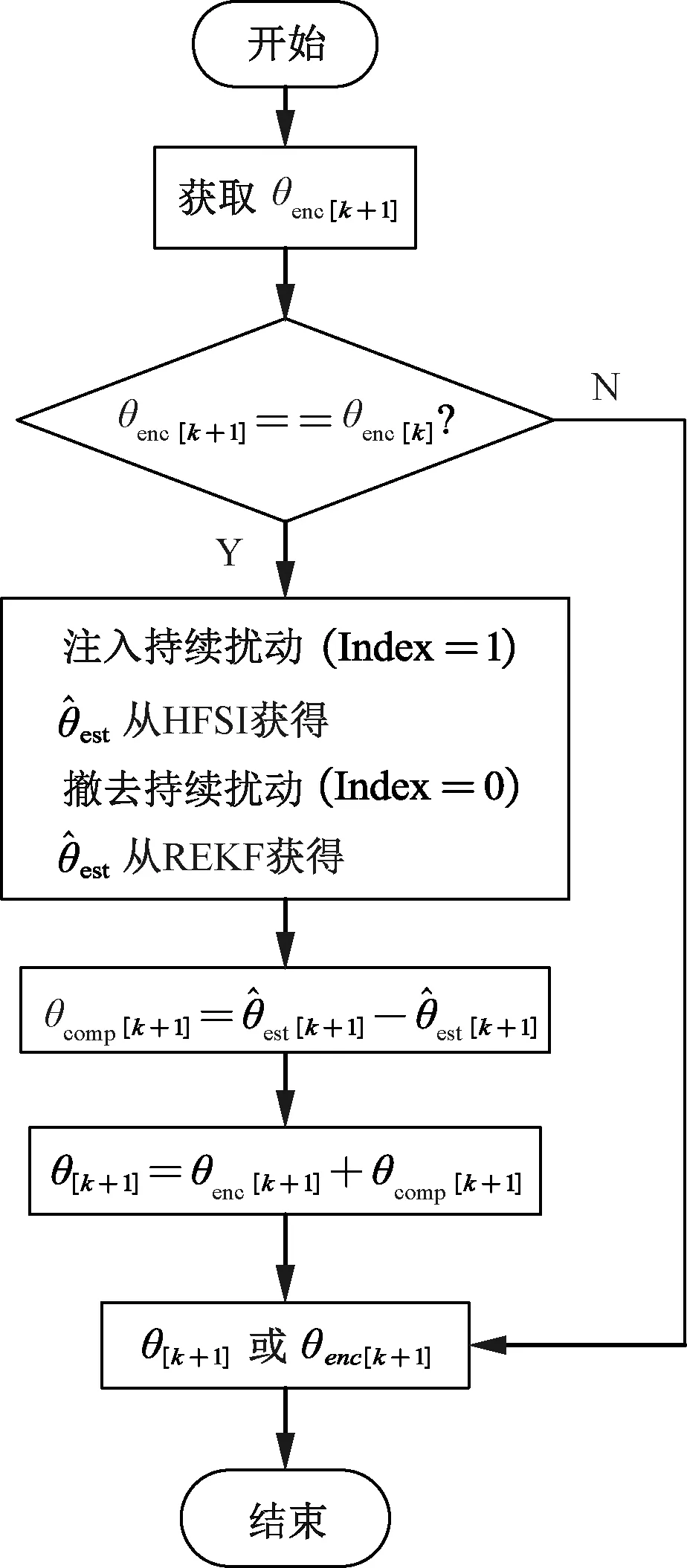
图3 改进插值算法执行流程图

插值算法实施的过程表述如下：若当前时刻编码器的位置与上一采样时刻的编码器位置相同，则编码器位置信息未更新，此时位置信息采用上一时刻编码器的位置信息，当标志位Index=0时，利用REKF计算出的实时位置信息获取当前相邻两个时刻位置的差值，与前一时刻的累加值进行累加运算后输出累加值，当标志位Index=1时，将当前时刻编码器的位置赋值给PI控制器中的积分器，可加速高频位置注入位置观测器收敛速度，同时，利用HFSI计算出的实时位置信息获取当前相邻两个时刻位置的差值，与前一时刻的累加值进行累加运算，然后输出累加值。否则，若当前时刻编码器的位置与上一采样时刻的编码器位置不相等，则将当前时刻的编码器位置赋给插值位置，同时实时插值位置中的累加值清零。如此迭代，从而实现插值控制。下文将文献[14]中所用的插值算法约定为传统插值算法，插值过程中无Index=0过程；本文的改进控制策略约定为改进插值算法。基于上述所有环节，总体系统框图如图4所示，框图整体表示id=0的矢量控制。

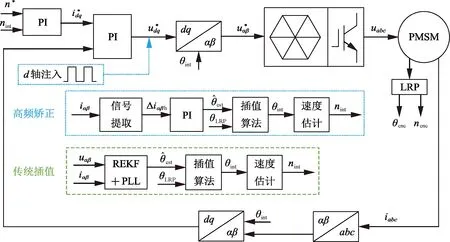
图4 控制系统简图

2 实验验证

实验用平台如图5所示。它为一套基于Speedgoat的PMSM驱动系统，直流母线电压设定为60V。上位机PC编译Simulink搭建矢量控制模型，再将编译后的C代码烧录至下位机Speedgoat。Speedgoat通过数字输入/输出(I/O)通道和模拟通道与驱动板相连，编码器实时的位置脉冲信号通过I/O通道传输至Speedgoat，反馈的三相电流信号则通过模拟通道传输。另外，负载设备采用了高精度的安川伺服电机。

图5 PMSM驱动平台

2.1 参数设置

PMSM驱动控制系统的采样频率与半导体器件的开关频率均为10kHz。驱动电机参数如表1所示，其轴端处安装2 500线增量式光电编码器，需降低位置信息更新频率，从而模拟低线数编码器。文中位置更新频率是500Hz，参考速度50r/min时，此时等效编码器线数为2 500×250/10 000=62.5线。在降阶卡尔曼滤波算法中，待定参数设置如下：Q=diag [0.1，0.1，1 000]，R=diag [0.2，0.2]，P0=diag [0.2，0.2，0.01]，x0=[0 0 0]T。反电动势滤波算法中收敛系数l2=25。降阶卡尔曼滤波算法中位置观测器中的PI控制器参数设置如下：kp=200，ki=300。高频注入位置观测器中PI控制器参数设置：kp=200，ki=300，注入的高频电压信号频率为2.5 kHz，幅值为10 V。

表1 测试电机参数

2.2 实验结果分析

图6是50 r/min时的α轴反电动势分量波形，对比滤波前后波形发现，滤波后比滤波前的反电动势波形更平滑，且两者相位基本一致。由此可知，本文的自适应滤波策略可有效滤除反电动势谐波。

图6 α轴反电动势分量波形

图7是传统插值算法在不同转速下受到瞬态扰动时的波形。图7(a)～图7(c)分别表示插值位置波形图和插值位置误差图。LRP表示低分辨率编码器位置，INT表示插值算法位置。插值位置误差是高精度编码器减去插值位置，RMSE表示均方根插值误差，ME表示最大插值误差。图7中，0.5 s处注入1 ms扰动，2.5 s处注入10 ms扰动，幅值均为2.4 N。分析控制系统受到1 ms扰动的情况，从图7可以得出，在不同参考转速条件下，1 ms的瞬时外界扰动对插值算法影响小，电机转子无反转现象，插值误差的峰值均在0.1 rad内，随后插值误差迅速衰减至稳态误差带(±0.03 rad)。分析控制系统受到10 ms扰动的情况，从图7可以观察到，10 ms的瞬时外界扰动对插值算法影响较大，电机转子出现短暂的反转现象，插值误差峰值均在0.4 rad内，受瞬时10 ms扰动后插值误差迅速衰减至稳态误差带(±0.03 rad)，衰减持续时间约为0.3 s。基于上述可得出传统插值控制算法抗外界瞬时扰动性能较好。

图8～图10是不同参考转速下(10 r/min、30 r/min、50 r/min)，传统插值算法与改进插值算法受到持续扰动时的插值位置和插值位置误差波形图，图中含义与瞬态扰动实验分析处相同。在图8～图10中，电机初始负载为0.5 N，1～3 s时间段施加1 N的外界持续扰动。

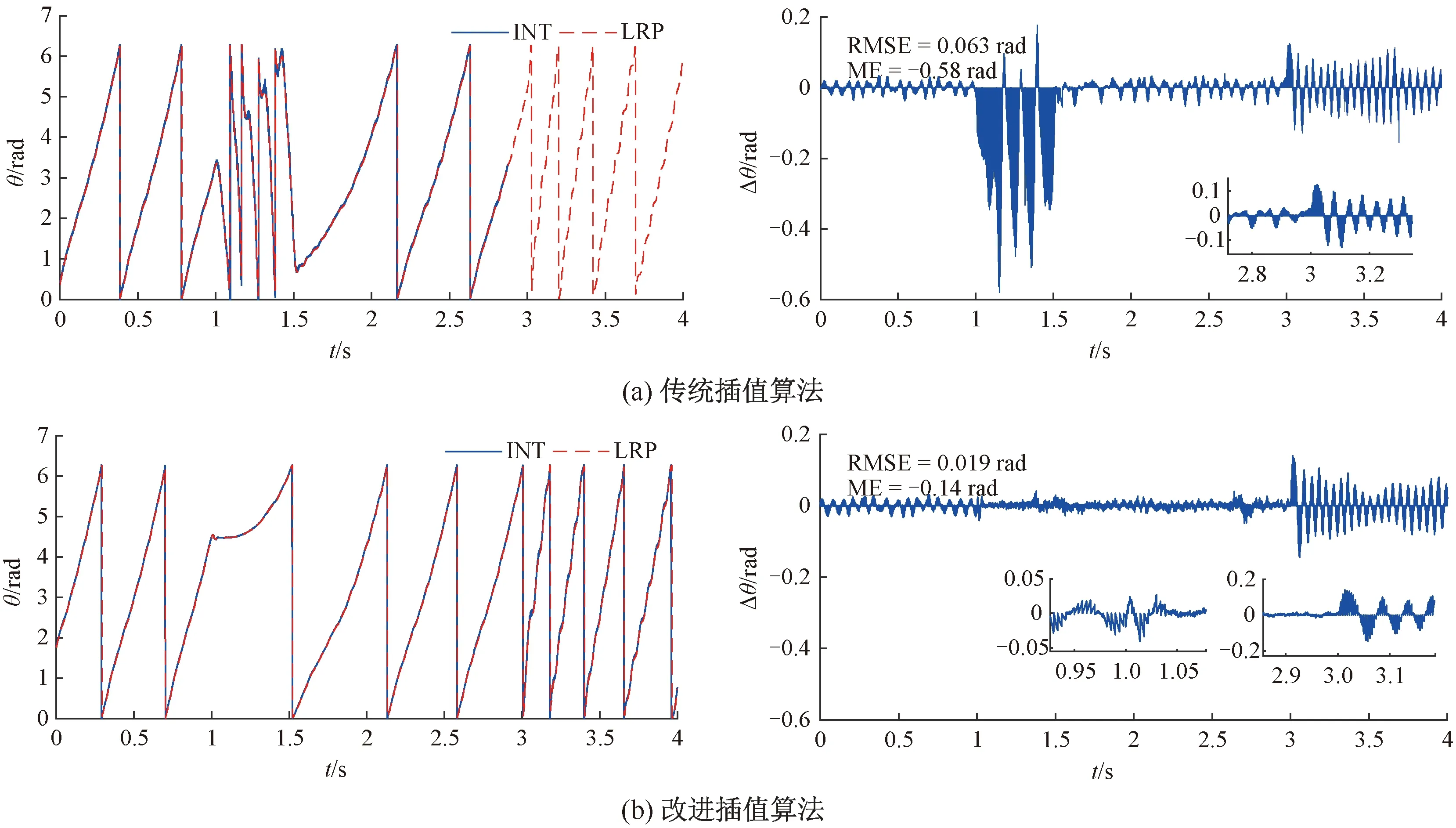
图9 参考转速30 r/min，受到持续扰动时的插值位置和插值位置波形

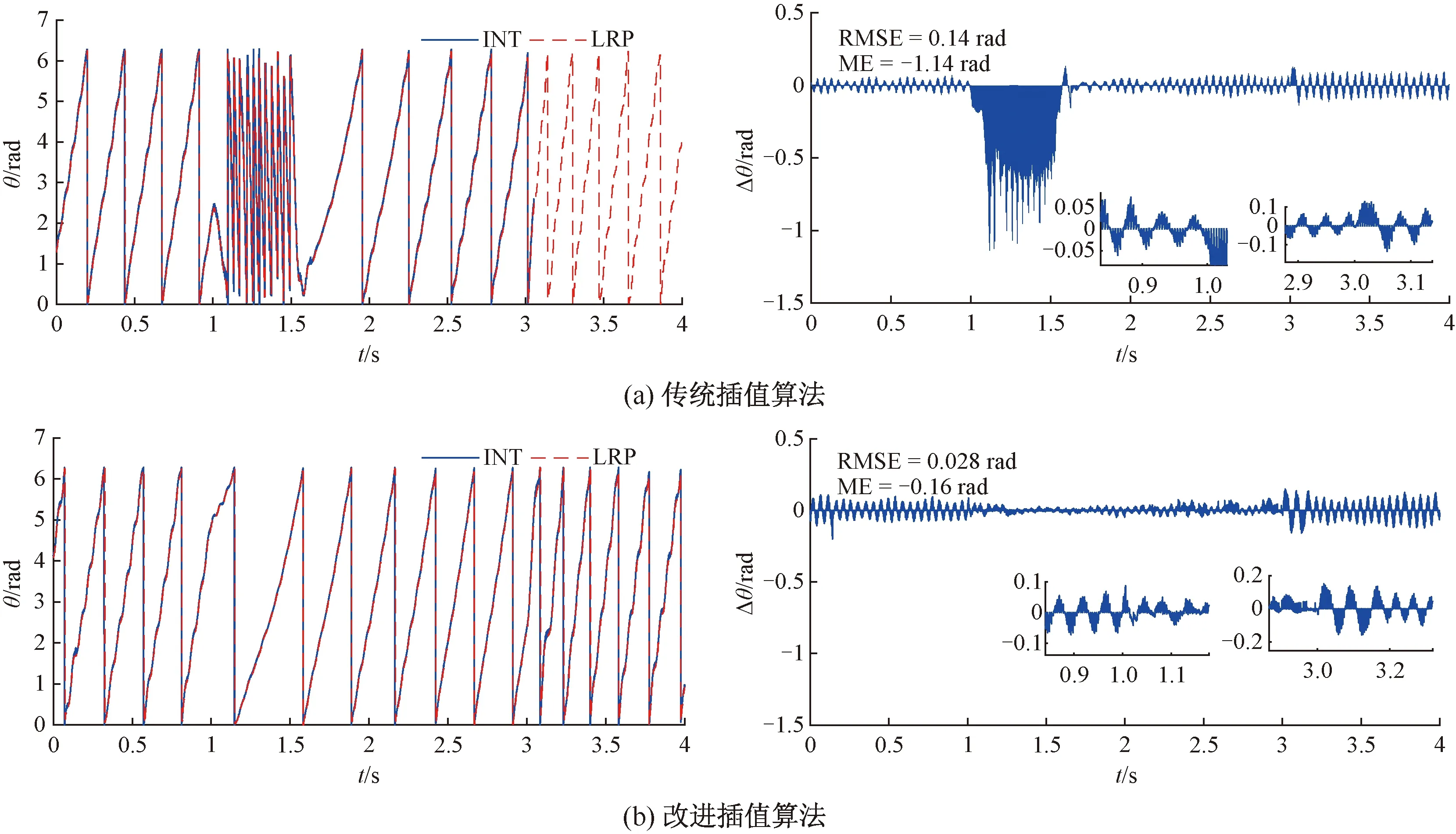
图10 参考转速50 r/min，受到持续扰动时的插值位置和插值位置波形

传统插值算法对持续扰动的鲁棒性能较差，驱动系统在受到1 N的外界持续扰动后，在30 r/min与50 r/min速度工况下出现明显的反转现象，持续时间约为0.5 s，随后转子恢复正转。由图8(a)、图9(a)、图10(a)可以观察到，在施加持续外界扰动后，插值位置误差显著增加，插值算法误差峰值在10 r/min、30 r/min、50 r/min时分别为0.58 rad、0.6 rad、1.2 rad，在30 r/min和50 r/min时，插值位置误差增大，且持续一段时间后，插值误差衰减至稳态误差带内。从图8(b)、图9(b)、图10(b)可分析出，在相同转速下，与传统插值算法相比，在外界持续扰动存在期间(1～3 s)，改进插值算法的插值位置误差带在±0.05 rad内，说明改进插值算法抗外界持续扰动性能较好。在撤去外界持续扰动后(3 s后)，从图8(b)、图9(b)、图10(b)中可观察到，插值位置误差会短暂增大，随后传统插值算法与改进插值算法的插值位置误差都快速恢复为施加扰动之前的水平。

3 结 语

基于高频注入算法，本文提出了一种抗外界扰动的位置插值策略，无需额外硬件和复杂计算，可准确地估计出驱动系统在受到持续扰动时的转子位置，从而提高了传统插值算法的抗扰动性能，保证驱动系统稳定运行，其有效性在PMSM驱动平台上得到了验证。而在电机参数变化较大的应用中，未来的深入研究将结合参数辨识理论，建立精确的高频模型，进一步优化该位置插值算法。