函数列统计半α收敛与统计半一致收敛

陈梦娜

（闽南师范大学数学与统计学院,福建 漳州 363000）

众所周知,连续函数列的极限函数不一定是连续函数.因此,分析中的一个核心问题是：在连续函数列中添加什么条件才能保持极限函数的连续性？1841年,Weierstrass证明了函数列一致收敛是极限函数连续的充分条件.1878年,Dini给出了极限函数连续弱于一致收敛的充分条件.Arzela在文献[1]中证明了极限函数连续的一个充要条件,在该条件下,紧致区间上实值连续函数列的极限函数是连续的,他将这一条件称为“逐段一致收敛”,Borel[2]将此称为“拟一致收敛”.Bartle[3]将Arzela 的结果推广到拓扑空间的实值连续函数网.1948年,Alexandroff[4]研究了从拓扑空间（不一定紧）到度量空间的函数列的极限函数连续性问题.函数列的α收敛性早在20世纪初已经被研究.2008年,Gregoriades 等[5]引入函数列exhaustiveness的概念,它能够刻画函数列的α收敛和逐点收敛的关系.

统计收敛的概念最初由Fast[7]和Steinhaus[8]分别独立引入,它是一般收敛的推广.自引入后,统计收敛逐渐引起研究者的兴趣.特别是20世纪80年代以来,统计收敛已成为人们研究的热点问题之一.统计收敛在不同领域都有应用,如数论[11]、可和性理论[12]、三角级数[13]、概率论[14]、测度论[15]、最优化[16]等.借助统计收敛,Caserta 等[9]定义了函数列的统计exhaustiveness,统计α收敛和弱统计exhaustiveness,并证明了统计极限函数连续与函数列弱统计exhaustiveness等价的条件.

最近Papanastassiou[6]定义了函数列的半α收敛、半一致收敛和半exhaustiveness,揭示了在极限函数连续的条件下,函数列半α收敛和半一致收敛相互等价.在函数列半α收敛与半一致收敛的定义中,要求函数列(fn)n∈N逐点收敛于函数f.因此,一个自然的问题是:如果将“逐点收敛”改为“逐点统计收敛”,将会得到什么样的结果?在文献[6]的基础上,借助统计收敛,定义了函数列的统计半α收敛与统计半一致收敛.通过构造例子说明,函数列的统计半α收敛区别于半α收敛、半α性质、逐点统计收敛以及统计α收敛，统计半一致收敛区别于半一致收敛.证明了在统计极限函数连续的条件下,函数列的统计半α收敛与统计半一致收敛相互等价.

1 预备知识

本文中,YX表示空间X到空间Y的所有映射的集合,C(X,Y)表示空间X到空间Y的所有连续映射的集合.

定义1[6]设(X,d)和(Y,ρ)是度量空间,x∈X,∀n∈N,fn∈YX.函数列(fn)n∈N在点x∈X处称为半exhaustive,若∀ε>0,∃δ>0,使的∀n∈N,∃m∈N 且m≥n,当y∈S(x,δ)时,有ρ(fm(y),fm(x))<ε.若函数列(fn)n∈N在X的每一点处都半exhaustive,则称(fn)n∈N半exhaustive.

定义2[6]设(X,d)和(Y,ρ)是度量空间,x∈X,∀n∈N,f,fn∈YX.若满足以下两个条件,则函数列(fn)n∈N在x∈X处称为半α收敛于f.即

1)fn(x)→f(x);

2)∀ε>0,∃δ>0,使得∀n∈N,∃m∈N且m≥n,当y∈S(x,δ)时,有ρ(fm(y),f(x))<ε.

若函数列(fn)n∈N在X的每一点处都半α收敛于f,则称(fn)n∈N半α收敛于f.满足定义2中条件2)的函数列称为具有半α性质.

定义3[6]设X是拓扑空间,(Y,ρ)是度量空间,∀n∈N,f,fn∈YX.若满足以下两个条件,则函数列(fn)n∈N在x0∈X处称为半一致收敛于f.即

1)fn(x0)→f(x0);

2)∀ε>0,存在x0的邻域V,使得∀n∈N,∃m∈N且m≥n,当x∈V时,有ρ(fm(x),f(x))<ε.

若函数列(fn)n∈N在X的每一点处都半一致收敛于f,则称(fn)n∈N半一致收敛于f.

定义4[9]设集合A是N的子集,对n∈N,令A(n)={k∈A:k≤n},若极限

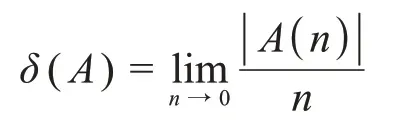
存在,则称δ(A)为A的渐进密度.此时有δ(NA)=1-δ(A)成立.若δ(A)=1,则称集合A是统计稠密的.设X是拓扑空间,x∈X,(xn)n∈N为X中的序列,若对x的任意邻域U,有δ({n∈N:xn∉U})=0,则称序列(xn)n∈N统计收敛于x,记作:

定义5[9]设(X,d)和(Y,ρ)是度量空间,∀n∈N,fn∈YX.函数列(fn)n∈N在x∈X处称为统计exhaustive,若∀ε>0,存在δ>0 和统计稠子集M⊂N,使得当y∈S(x,δ)且m∈M时,有ρ(fm(y),fm(x))<ε.若(fn)n∈N在X的每一点都统计exhaustive,则称函数列(fn)n∈N统计exhaustive.

定义6[9]设(X,d)和(Y,ρ)是度量空间,∀n∈N,f,fn∈YX.称函数列(fn)n∈N统计α收敛于f,若对于每个x∈X,及X中收敛到x的序列(xn)n∈N,序列(fn(xn))n∈N统计收敛于f(x),记作：

定义7[9]设(X,d)和(Y,ρ)是度量空间,函数列(fn)n∈N⊂YX在x∈X处称为统计弱exhaustive,若∀ε>0,∃δ>0,使得∀y∈S(x,δ),存在N的统计稠子集My,当n∈My时,有ρ(fn(y),fn(x))<ε.

2 主要结果及其证明

定义8设X是拓扑空间,(Y,ρ)是度量空间,x∈X,∀n∈N,f,fn∈YX.若满足以下两个条件,则函数列(fn)n∈N在x∈X处称为统计半α收敛于f.即

1)fn(x)f(x);

2)∀ε>0,存在x的邻域U,使得∀n∈N,∃m∈N且m≥n,当y∈U时,有ρ(fm(y),f(x))<ε.

若函数列(fn)n∈N在X的每一点处都统计半α收敛,则称函数列(fn)n∈N统计半α收敛于f.

由定义知半α收敛的函数列一定是统计半α收敛的.下面的例子说明统计半α收敛函数列不一定是半α收敛.

例1存在统计半α收敛的函数列,其不是半α收敛的.

证明∀n∈N,定义fn:R→R，有：

∀x∈R,令f(x)=1,则函数列(fn)n∈N⊂RR统计半α收敛于f.事实上,∀x∈R,fn(x)f(x).下证函数列(fn)n∈N满足半α性质.对任意ε>0,取x的邻域U=(x-1,x+1).∀n∈N,取大于n的非平方数m,则∀y∈U,有ρ(fn(y),f(x))=|1-1|=0<ε.故函数列(fn)n∈N统计半α收敛于f.另一方面,∀x∈R,数列fn(x)不收敛于f(x),从而函数列(fn)n∈N不是半α收敛于f.

下面的例子说明具有半α性质的函数列不一定是统计半α收敛.

例2存在具有半α性质的函数列,其不是统计半α收敛.

证明∀n∈N,定义fn:R→R，有

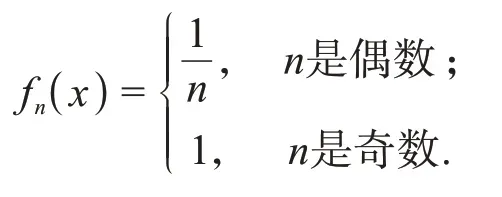
∀x∈R,令f(x)=0,类似例1中的证明,易知函数列(fn)n∈N具有半α性质.∀x∈R,数列fn(x)不统计收敛于0,所以函数列(fn)n∈N不统计半α收敛于f.

由定义知，统计半α收敛的函数列一定逐点统计收敛,但其逆命题不一定成立.下面的例子说明逐点统计收敛的函数列不一定统计半α收敛.

例3存在逐点统计收敛的函数列,其不是统计半α收敛.

证明∀n∈N,定义fn:R→R，有

令f(x)=则函数列(fn)n∈N⊂RR逐点统计收敛于f.另一方面,(fn)n∈N在x=0 处不满足半α性质.事实上,设0<ε< 1,δ>0,存在n∈N 使得<δ,对任意m∈N 且m≥n,那么取0的邻域U=(-δ,δ),则y=∈U∩(,+∞),且

|fm(y)-f(0)|=|0-1|=1>ε.ρ(fm(y)，f(x))≤ρ(fm(y)，fm(x))+ρ(fm(x)，f(x))<ε,

所以函数列(fn)n∈N不统计半α收敛于f.

命题1若X,Y是度量空间,(fn)n∈N⊂YX,f∈YX.若函数列(fn)n∈N统计α收敛于f,则(fn)n∈N统计半α收敛于f.

证明由文献[9]知,若(fn)n∈Nf,则∀x∈X,fn(x)→sf(x)且函数列(fn)n∈N统计exhaustive.下证(fn)n∈N具有半α性质.由fn(x)→sf(x)知,∀ε>0,存在N 的稠子集M1,当n∈M1时,有ρ(fn(x),f(x))<由(fn)n∈N统计exhaustive 知,存在x的邻域V和N 的稠子集M2,当y∈V且n∈M2时,有ρ(fn(y),fn(x))<所以存在m∈M1∩M2⊂N,当y∈V时，有

从而(fn)n∈N在x处统计半α收敛于f.由x的任意性知,函数列(fn)n∈N统计半α收敛于f.

上述命题的逆命题不一定成立,即统计半α收敛的函数列不一定统计α收敛.

例4存在函数列是统计半α收敛的,但不是统计α收敛.

证明∀n∈N,定义函数fn:R→R,当n为奇数时,fn(x)=当n是偶数时,

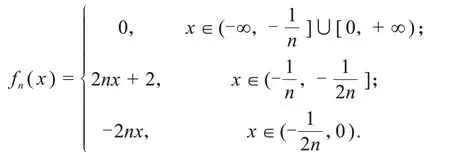
令f(x)=0,显然函数列(fn)n∈N统计逐点收敛到f.下证函数列(fn)n∈N具有半α性质.∀ε>0,存在x的邻域U,使得对任意n∈N,存在m取大于n的奇数,当y∈U时,有ρ(fm(y),f(x))=<ε.所以函数列(fn)n∈N统计半α收敛.另一方面,取xn=此时xn→0,而fn(xn)=1,并不逐点统计收敛于f(x)=0,所以函数列(fn)n∈N不统计α收敛于f.

综上知,函数列的收敛关系如图1所示.

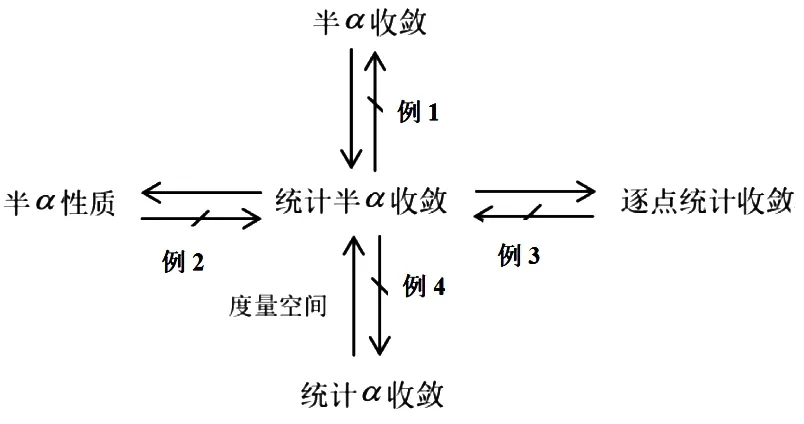
图1 函数列的收敛关系Fig.1 The relationships of convergence of sequences of functions

定义9设X是拓扑空间,(Y,ρ)是度量空间,∀n∈N,f,fn∈YX.若满足以下两个条件,则函数列(fn)n∈N在x0∈X处称为统计半一致收敛于f.即

1)fn(x0)f(x0);

2)∀ε>0,存在x0的邻域V,使得∀n∈N,∃m∈N且m>n,当x∈V时,有ρ(fm(x),f(x))<ε.

若函数列(fn)n∈N在X的每一点处都统计半一致收敛,则称(fn)n∈N统计半一致收敛.

由定义知函数列半一致收敛一定是统计半一致收敛,但其逆命题不成立.

例5存在统计半一致收敛的函数列不是半一致收敛的.

证明∀n∈N,设fn,f为例1 中定义的函数,则函数列(fn)n∈N统计半一致收敛于f.事实上,∀x∈X,fn(x)f(x).∀ε>0,存在x的邻域V,使得∀n∈N,存在m取大于n的非平方数,当x∈V时,有ρ(fm(x),f(x))=|1-1|<ε;另一方面,fn(x)不收敛于f(x)=1,则函数列(fn)n∈N不半一致收敛于f.

接下来证明本文的主要结果.

定理1设X是拓扑空间,(Y,ρ)是度量空间,f∈C(X,Y),(fn)n∈N⊂C(X,Y),则下列条件等价：

1)函数列(fn)n∈N统计半α收敛于f;

2)函数列(fn)n∈N统计半一致收敛于f.

若有1)或2)成立,则函数列(fn)n∈N半exhaustive且∀x∈X,fn(x)f(x).

证明1)⇒2)由已知∀x∈X,fn(x)f(x).由函数列(fn)n∈N的半α性质知,∀ε>0,存在x的邻域V1,使得∀n∈N,∃m∈N 且m>n,当y∈V1时,有ρ(fm(y),f(x))<又因为f连续,存在x的邻域V2,使得当y∈V2时,有ρ(f(x),f(y))<令V=V1∩V2,则当y∈V时,有

ρ(fm(y)，f(y))≤ρ(fm(y)，f(x))+ρ(f(x)，f(y))<ε.

从而(fn)n∈N在x处统计半一致收敛于f.由x的任意性知,函数列(fn)n∈N统计半一致收敛于f.

2)⇒1)由已知∀x∈X,fn(x)→sf(x).因为函数列(fn)n∈N统计半一致收敛于f,∀ε>0,存在x的邻域U1使得∀n∈N,∃m∈N且m>n,当y∈U1时,有ρ(fm(y),f(y))<又由f的连续性知,存在x的邻域U2,使得,当y∈U2时,有ρ(f(y),f(x))<取U=U1∩U2,当y∈U时,有

ρ(fm(y)，f(x))≤ρ(fm(y)，f(y))+ρ(f(y)，f(x))<ε,

从而(fn)n∈N在x处统计半α收敛于f.由x的任意性知,函数列(fn)n∈N统计半α收敛于f.

因为1)与2)等价,不妨设条件2)成立.显然有fn(x)f(x)成立.下证函数列(fn)n∈N半exhaustive.因为(fn)n∈N统计半一致收敛于f,∀ε>0,存在x的邻域W1使得∀n∈N,∃m∈N 且m>n,当y∈W1时,有因为f是连续的,则存在x的邻域W2,使得当y∈W2时,有所以当y∈W1∩W2时,有

ρ(fm(y)，fm(x))≤ρ(fm(y)，f(y))+ρ(f(y)，f(x))+ρ(f(x)，fm(x))<ε.

从而(fn)n∈N在x处半exhaustive.由x的任意性知,函数列(fn)n∈N半exhaustive.