基于纠缠交换的量子安全多方求和
林 崧,常 泓
(1.福建师范大学计算机与网络空间安全学院,福建 福州 350007;2.福建师范大学数字福建环境监测物联网实验室,福建 福州 350007;3.福建师范大学数字福建大数据安全技术研究所,福建 福州 350007)
安全多方计算(SMC)[1-2]使多个参与方能够基于其私人输入进行联合计算,同时保持输入的私密性.作为现代密码学的一个重要分支,安全多方计算被广泛应用于私人拍卖、无记名投票选举、电子商务和数据挖掘等领域.经典SMC 的安全性是基于计算复杂性的假设.然而,随着量子算法的提出,它变得越来越脆弱,例如Grover 搜索算法[3]和Shor 搜索算法[4].与此同时,Bennett 等[5]在1984年提出了一个理论上无条件安全的密钥分发协议,即著名的BB84 协议,这引起了人们将经典密码原语扩展到量子力学领域的兴趣.最近,人们提出了各种量子安全多方计算协议,如量子私密查询[6-9],量子保密比较[10-14],量子安全多方求和[15-21]等.
安全多方求和是现实生活中常见的安全任务,它是需要构建复杂安全系统的一个基础原语协议.在一个简单的安全多方求和方案中,有n参与者,每个参与者都有一个秘密数据.他们希望在不泄露任何秘密输入信息的情况下,正确计算这些输入的总和.2007年,Vaccaro 等[15]提出了一种量子安全多方求和协议,用于实现匿名投票和调查的安全任务.在这个协议中,参与者向可信的计票员发送秘密消息,计票员计算并公布汇总结果.同年,Du等[16]设计了一个基于非正交单粒子的量子秘密求和协议,该协议允许参与者以串行方式将其私有数据累积到未知数,从而实现安全多方求和的目标.该协议能够抵抗n-1参与者的共谋攻击,并实现渐近安全.2018年,Yang 等[17]提出了一个基于量子傅里叶变换的安全多方量子求和协议.随后,Zhang 等[18]利用隐形传态设计了一个巧妙的量子安全多方量子求和协议.考虑参与者的实际情形,Sutradhar 等[20]于2020年结合著名的Shamir门限秘密共享,提出了一个(t,n)门限量子安全多方量子求和协议,实现部分参与者安全求和任务.在此基础上,提出了一种基于纠缠交换的量子安全多方求和(QSMMS)协议.协议中,Bell态和cat态作为信号粒子在参与者之间传输,并根据这些纠缠粒子的相关性设计相应的窃听检测,进而确保了这些粒子传输的安全性.参与者的秘密数据通过纠缠交换进行嵌入到这些粒子中,并在第三方的帮助下获得计算结果.在这里,要求第三方是半信任的,也就是说,她被允许行为不当,但不能与任何一方串通.
内容安排如下:第1节介绍了本文所涉及的一些预备知识.第2节对本文所提出的量子安全求和方协议进行描述,该协议的安全性分析将在第3节给出.第4节小结本文.
1 预备知识
在描述协议之前,先来介绍一下所用到的预备知识.在一个d级量子系统中,量子傅里叶变换是一种常用工具,可描述如下:

其中,ξ=所以,可直接构造两个常见的相互无偏基,B1=,且除了F外,X和Z也是常见操作:
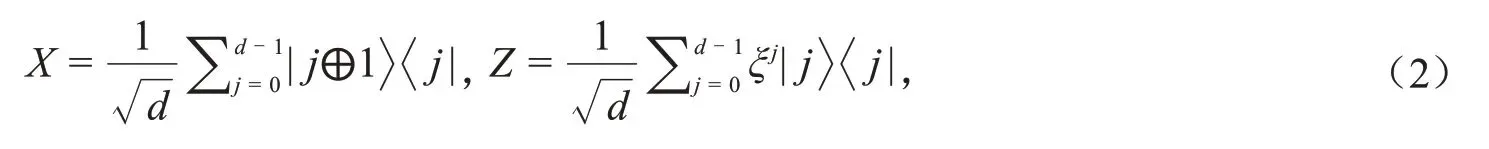
其中,符号⊕表示累加模d.d级Bell态是EPR对在d级量子系统中的推广,可表示为以下形式:
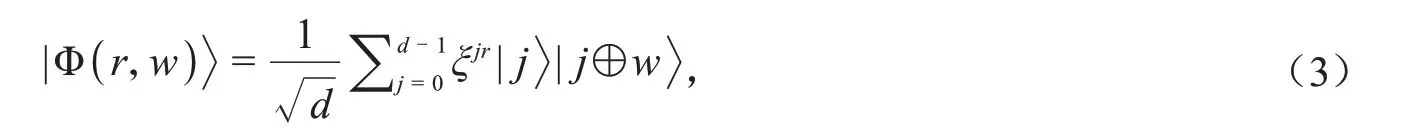
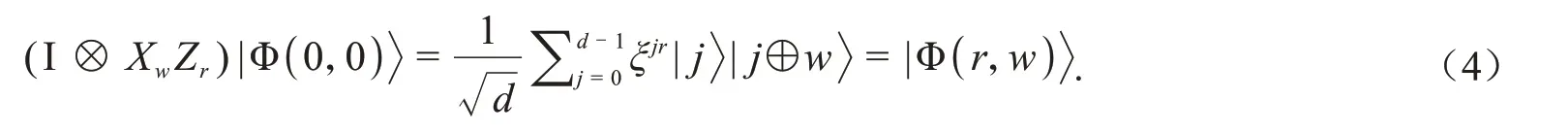
除了Bell态,cat态是另一种更为普通的纠缠态.一个d级n粒子cat态可描述为:
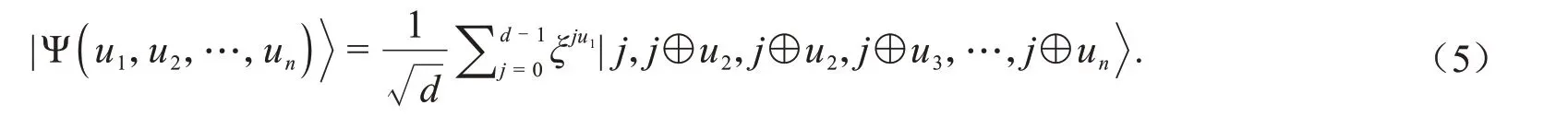
其中u1,u2,…,un∈D.在所提协议中,用到了一类特殊的cat态,即
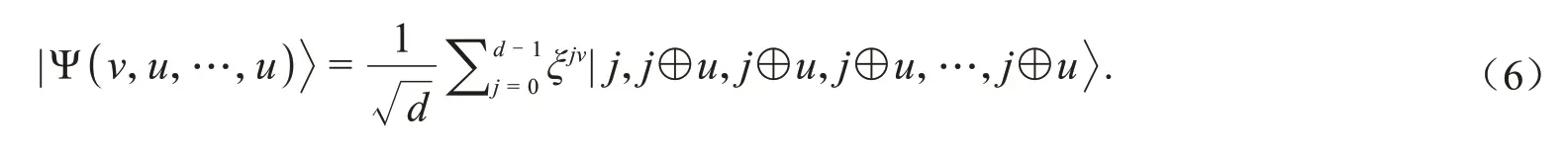
对该量子态通过不同基进行测量,所得的测量结果具有一定的关联性.利用该关联性,通过简单计算可得到以下结论.
定理1一个(n+1)-粒子态是态|Ψ(v,u,…,u),当且仅当它满足以下两个条件时:
(R1)当B1基测量每个粒子时,n+1个测量结果满足k0⊕u=k1=k2=···=kn;
(R2)当B2基测量每个粒子时,n+1个测量结果满足k0⊕k1⊕k2⊕···⊕kn⊕v=0.
在接到编报实施方案的通知前,项目建管单位应与设计单位加强沟通协作,做好项目区的工程勘察、测量等基础资料收集及实施方案编制的各项准备工作,一旦经费落实,立即编制上报;提前做好自筹资金落实、群众投工投劳组织协调和施工占地协调等各项准备工作,为项目顺利实施创造条件。
纠缠交换[22]作为量子信息处理的一个重要的资源,在量子计算、量子隐性传态、密集编码和量子密码等领域中得到广泛的应用.它可使得从未直接发生相互作用的量子系统产生纠缠,利用纠缠交换可达到实现信息传递的目的.例如,在一个由1 个n-粒子cat 态|Ψ(v,u,…,u)和n个Bell 态|Φ(ri,wi)〉(i=1,2,…,n)构成的量子系统中,当对cat 态粒子和每个Bell 态的一个粒子进行Bell 态测量时,剩余的粒子会坍缩成某一特定的纠缠态.具体来说,Bell态和cat态的纠缠交换的整个过程可以用下面的公式表示,
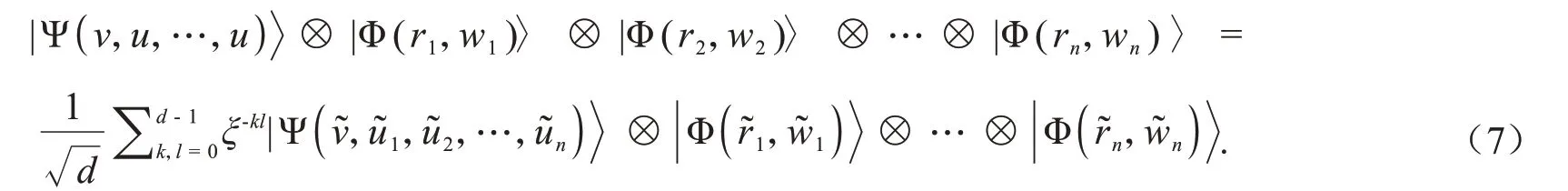
这里
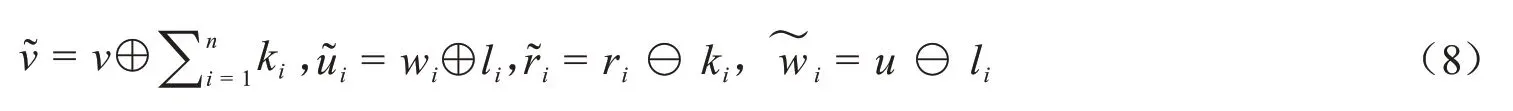
其中符号⊖表示减法模d.
2 量子安全多方求和协议
在所提协议中,有n个相互不信任的参与者,标记为P1,P2,…,Pn,并且每个参与者Pi(i=1,2,…,n)都有一个私密数据集这里,可设…m}且d>sup{S}.在一个半可信的第三方(TP)的帮助下,P1,P2,…,Pn可利用下述步骤联合计算总和并保持各自数据集Di的私密性.
1)每一方P(ii=1,2,…,n)都准备个L+σ个d级Bell态,其中,下标hji和表示一个纠缠对中两个不同的qudits,且(jj=1,2,3,…,L+σ)表示纠缠对的顺序.Pi从每个Bell 态中分别取出hji和tij粒子,形成两个有序的粒子序列Hi=(h1i,h2i,…,hLi+σ)和Ti=(ti1,ti2,…,tiL+σ).TP制备L+nδ个d级cat 态并从每个cat 态|ψ(vj,uj,uj,…,uj)中取出sji形成n+1个有序序列S0=其中下标j=1,2,…,L+nδ表示粒子的顺序.
2)TP保留粒子序列S0在自己手中,并将Si发送给Pi.同时,Pi发送粒子序列Ti给TP,并保留粒子序列Hi.以上粒子传输过程在图1中展示.
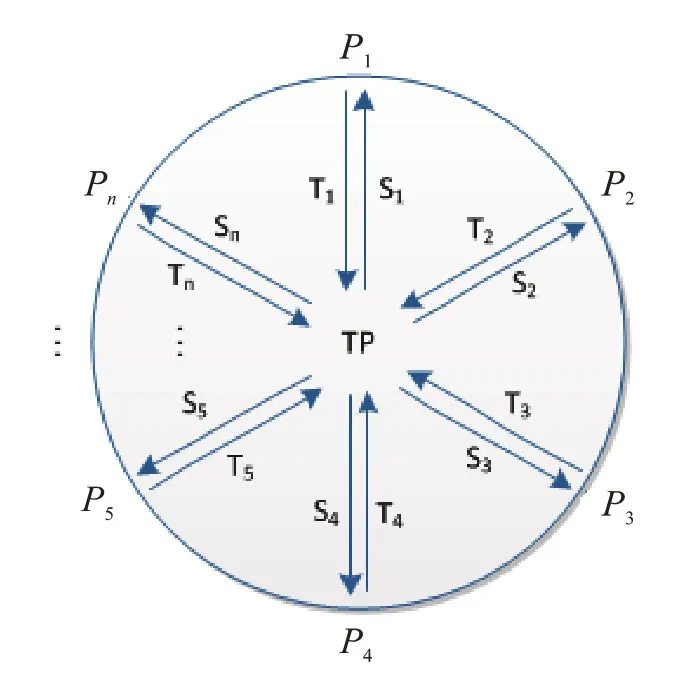
图1 TP和Pi的分发过程Fig.1 The particle transmission process between TP and each Pi
3)在TP和参与者都确认接收到粒子序列后,n+1方(TP和n个参与者)合作执行以下两个窃听检测.
检测1首先,Pi从Si中随机选择δ个粒子作为样本.对于每一个样本粒子,Pi随机选择B1基或B2基对粒子进行测量.然后Pi要求TP 和其他n-1 个参与者对相应粒子用相同的基进行测量,之后,TP 宣布样本粒子的初态和她的测量结果k0,然后,n-1 个参与者以随机顺序宣布他们的测量结果.根据公布的信息,Pi能检查测量的结果是否满足条件(R1)和(R2).用这种方式,Pi能计算出错误率.一旦错误率高于某一确定的阈值,将放弃协议.否则,将继续执行.
检测2首先,TP 从每个Ti(i=1,2,…,n)中随机选择σ 个粒子作为样本.对于每一个样本粒子,TP 随机选择B1基或B2基对粒子进行测量.然后TP 要求Pi对相应粒子用相同的基进行测量,之后,Pi将他的测量结果告知TP.根据公布的信息,TP 能检查测量的结果是否满足条件(R1)和(R2).用这种方式,TP 能计算出错误率.一旦错误率高于某一确定的阈值,她将放弃协议.否则,将继续执行.
4)Pi(i=1,2,…,n)对他的私密数据集进行编码.具体地说,Pi随机产生一个变量rji,进而得到wji=这样就使得xji=rij⊕wji.随后,Pi对手中粒子串Hi的第j个粒子进行操作.这样,该两粒子纠缠态将从变为然后,他对粒子sji和粒子hji进行Bell 态测量.假设该测量结果是,其中最后,Pi计算

并将该经典信息告诉TP.
5)当所有参与者都执行上述操作后,就发生纠缠交换,即TP 手中的对应粒子sj0和t1j,t2j,…tnj坍缩到某一个cat态.这样,TP对这些粒子进行测量,就可得到相应的测量结果.不妨设该态为那么因此,TP就可根据测量结果和经典信息qji,推得求和结果,即

最后,TP公布该求和结果.
3 安全分析
在本节中,对所提协议的安全性进行分析.TP 和参与者之间的量子信道的安全性由窃听检测过程保证.因此,明显地,直接窃取信息是不可行的.内部攻击比外部攻击更有力,故专注于内部攻击.此外,TP不完全可信,也可能窃取秘密输入.因此,本文将分别讨论这两种攻击,即不诚实的参与者的攻击和半可信的TP的攻击.
3.1 不诚实的参与者的攻击
此种攻击中,设Pm(记为P*m)是不诚实的且想窃取多有或者部分有关Pl的私密数据的信息.他能执行两个常见攻击策略中的一种去攻击本章所提协议,具体描述如下.
Case1:截获重发攻击在步骤2)中,TP传输序列Sl给Pl,Pl传输序列Tl给TP.因此,P*m能利用这次机会去执行他的攻击.具体地,P*m制备几个假粒子,并用这些假粒子代替信号粒子.我们先来分析TP 传输序列Si给Pi的情况.序列Sl包含了部分Pl的信息,当它在步骤2)中传输时,P*m拦截这个粒子序列.拦截后,P*m可通过测量得到在步骤4)中用于计算的u值.然而,这种行为在检测1中会被发现.因此,这个攻击将会失败.接下来,分析Pi传输序列Ti给TP 的情况.类似地,当序列Tl在步骤2)中传输时,P*m拦截并测量这个粒子序列.在那之后,P*m能获得步骤4)的计算过程中wjl的值.然而,这种行为在检测2 中会被发现.因此,这个攻击也将会失败.结果,这个协议对于截获重发攻击是安全的.
Case2:纠缠附加粒子攻击此种攻击中,首先分析Pi传输序列Ti给TP 的情况.在Pl发送序列Tl给TP之前,P*m制备一个附加粒子并执行一个确定的酉操作在这个附加粒子和序列Tl的传输粒子上,这将使得两个粒子变为纠缠态.协议最后,他将利用这个附加粒子来窃听Pl的所有或者部分信息.接下来,将说明即使他拥有无限的计算能力,由于技术受到量子力学定律的限制,在检测2中不引入错误的情况下,P*m不能获得任何关于Pl秘密输入的信息.
Pm*对序列Tl中粒子tlj(粒子T)和纠缠附加粒子(粒子E)的最一般操作如下:

其中f∈D.态是由U唯一确定的纯态.从U的幺正性可得出如下条件:

其中f,f′∈D.当f≠f′(或f=f′),δf,f′=0(或1).
在P*m执行完U操作后,粒子H、T和E组成的粒子系统将变为如下状态,
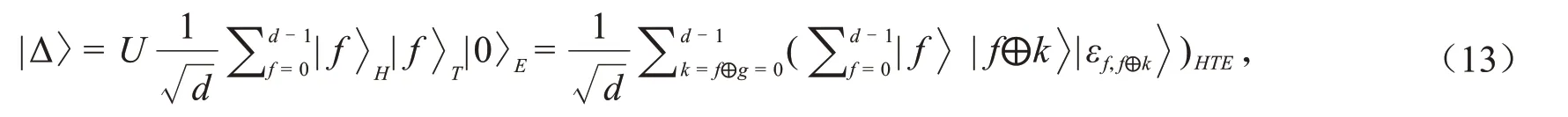
检测2中,可从条件(R1)得到

根据公式(13~14),可进一步得到
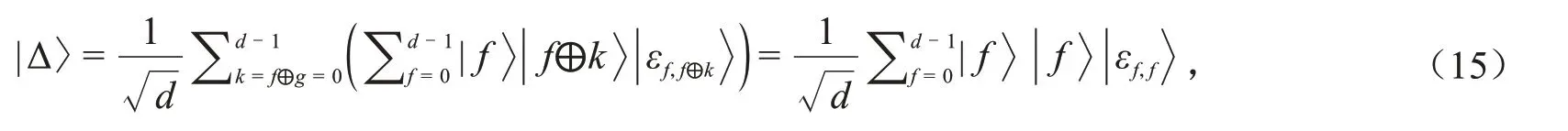
当Pi和TP用B2测量粒子时,系统的态可写为:
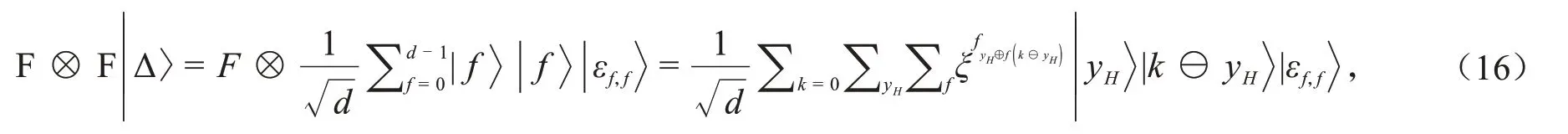
从条件(R2)可得
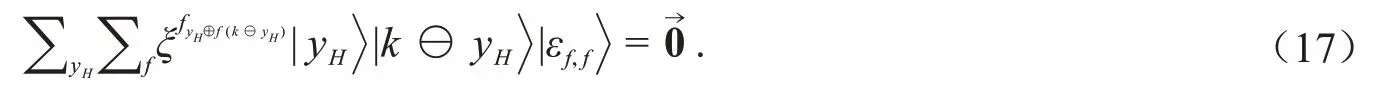
通过计算可得

进而可推得

这样,就成功推出Pm*成功窃听的条件.当Pm*纠缠一个附加粒子在粒子T 上,f等于g的概率为当一个检测序列有σ个粒子,f等于g的概率是当σ趋于无穷大,P*m成功窃听的概率趋于0.P*m窃听Sl的情况与上类似.
3.2 半可信的TP攻击
现在,来简要讨论一下TP企图窃听私密数据的情况.在所提协议中,TP被允许自己行为不当,但不会与任何参与者合谋.为了得到参与者的有用信息.TP 必须获取参与者的r和w粒子,而不向检测中引入任何错误.如果TP 诚实的执行协议,在纠缠交换前,她在步骤2)中通过测量可得到vj,uj和wji.在步骤4)中,纠缠交换后,由于Pi的公布,TP 可知即在步骤5)中,可测量得到和.当协议结束时,他就可知即使TP 知道如此多的信息,他也不能窃听到rij⊕wji的值.如果TP 采取截获重发攻击和纠缠附加粒子攻击,则分析结果与上节相同.
4 结语
提出了一个利用cat态和Bell态的纠缠交换来实现多方安全求和的量子协议.协议中,半可信第三方TP制备cat态并将这些信号粒子发送给每个参与者,每个参与者制备Bell态并将其中的一个粒子发给TP.然后,每个参与者通过对Bell态粒子进行相应的局域幺正操作,嵌入各自的私密数据,进而对手中的粒子的Bell基测量实现纠缠交换.最后,TP根据对手中cat态的测量结果和公开信息推得这些私密数据的异或和.通过对协议中的一些常见内部和外部攻击下的分析,表明所提协议在理论上是安全的.同时,由于信号粒子在信道中仅进行一次单向传输,常见的物理攻击,如木马攻击[20-21],对所提协议也是无效的.虽然近年来量子技术取得长足的基本,但协议所涉及的d级cat态和d级Bell态的制备和测量在当前技术条件下仍然是困难的,特别是随着d的增大和粒子数目的增多制备成功概率大大降低.因此,描述了一种理论上可行的量子安全多方求和协议,协议的实现还需要量子技术的进一步发展.

