浅析整体思想在数学教学中的应用
许含洁

[摘 要] 整体思想表现在思考问题时,打破思维的局限性,将视线放到问题的整体结构中,从宏观层面全面地观察问题的本质,将一些独立却又相关的量视为一个整体进行处理. 文章探讨了整体思想在求图形面积、方程、整体操作以及应用题中的应用.
[关键词] 整体思想;数学教学;方程;应用题
数学整体思想是以数学事物的整体性质为着手点,强调对其结构进行整体性的改造与分析,从“集成”的角度将一些图形或式子等打包为一个整体,进行整体处理的数学思想[1]. 这种思想方法在数学教学中应用得较多,如解方程(组)、代数式的求值或化简、几何证明等均有涉及. 一般以整体运算、设元、代入、补型等方式进行操作. 笔者从自身的执教经验出发,从以下几方面谈谈整体思想的实际应用情况,与读者共勉.
在求图形面积中的应用
纵观近些年的中考数学题,关于求图形面积的问题屡见不鲜且灵活多变,此类试题虽新颖有活力,但也给部分学生带来了困扰. 一些基础不够扎实,数学思想方法欠缺的学生看到此类问题打心底就感到恐惧. 笔者研究了不少关于求图形面积的问题,发现此类问题若从整体思想的角度去分析,常能起到事半功倍的效果.
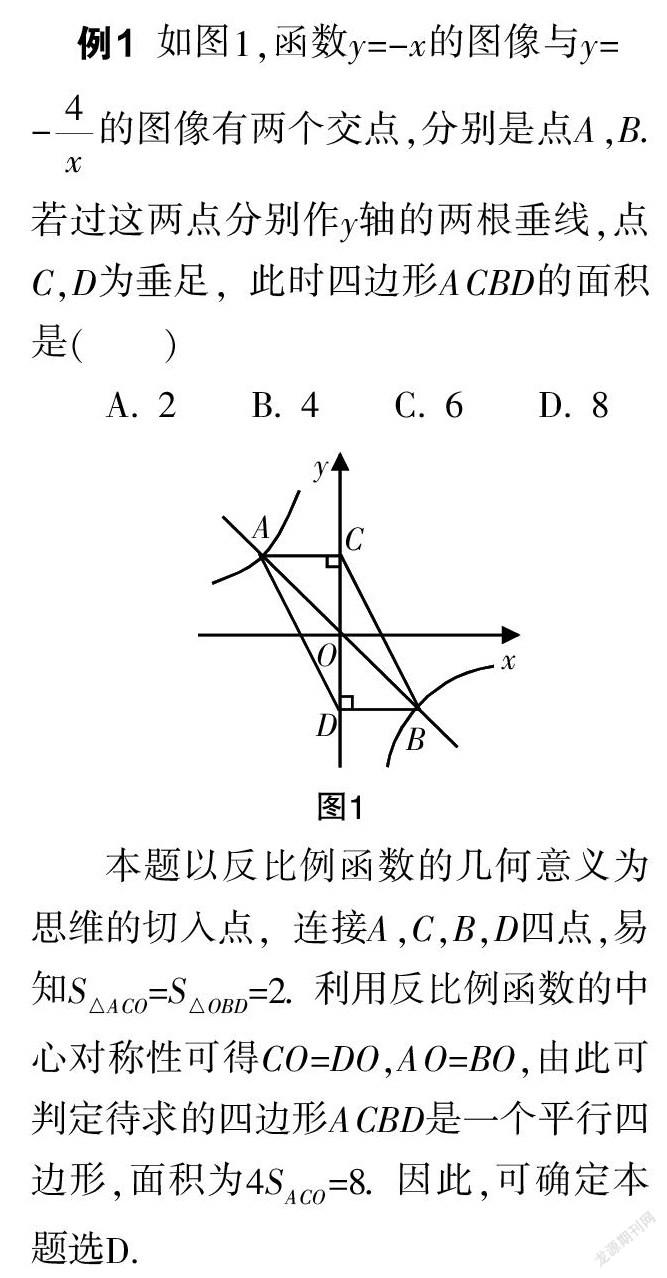
例1 如图1,函数y=-x的图像与y= -的图像有两个交点,分别是点A,B. 若过这两点分别作y轴的两根垂线,点C,D为垂足,此时四边形ACBD的面积是( )
A. 2 B. 4 C. 6 D. 8
本题以反比例函数的几何意义为思维的切入点,连接A,C,B,D四点,易知S=S=2. 利用反比例函数的中心对称性可得CO=DO,AO=BO,由此可判定待求的四边形ACBD是一个平行四边形,面积为4S=8. 因此,可确定本题选D.
本题从反比例函数的几何意义、对称变换的角度进行思考与分析,把图像中呈现的一些零碎且毫无规则可言的图形转化成学生所熟悉的规则图形. 学生面对转化后的平面图形,解题思路变得清晰.
整体思想在求图形面积时最大的功能是将神态各异的不规则图形,转化为我们所熟悉的特殊图形来进行解决. 这种方法不仅能启发学生的数学思维,还能有效地培养学生的创新意识,让学生在探索与思考中实现解题的创新,提升数学能力.
在方程组中的应用
整体思想主要体现在摒弃局部思维,从大局着手进行整体观察与分析,以探寻新的解决问题的途径. 代数问题的解决中,我们常发现将它们进行合并能消元或凑成整数,一般称这种操作为整体合并,最常用的整体合并方式有错位合并、配方合并、首尾合并等.
二元一次方程组是初中数学教学的重点与难点,教师可引导学生从二元消为一元的角度去分析问题. 这就涉及加减消元与代入消元的问题,不论是哪种消元都需要将一部分内容视为整体进行使用.
例2 已知x,y满足方程组2x+y=1009,x+2y=-1006,求x2-y2的值.
本题若按照正常解题思路分析,需分别计算出x与y的值,再计算x2-y2,此过程异常烦琐,增加计算量的同时也会导致错误的发生. 若换一种思维角度,运用倒推法从结论着手,x2-y2可写成(x+y)(x-y),只要能分别计算出(x+y)与(x-y)的值,此题的答案便呼之欲出.
将方程组中的两个式子相减,即2x+y-(x+2y)=1009-(-1006),计算可得x-y=2015;将方程组中的两个式子相加,即2x+y+x+2y=1009-1006,计算可得3x+3y=3,x+y=1. 所以x2-y2=(x+y)(x-y)=1×2015=2015.
通过两个式子整体的加减,我们很快地解决了问题,这种解题思路既简洁又方便. 解方程组时遇到数字大的情況,计算会异常繁杂,这是一个棘手的问题,学生一不小心就会出现失误. 此时,将未知数的系数作为观察的点,若两个方程中未知数的系数具有一定的关联性,则可进行整体加减,将数值化小,获得简易方程,由此达到事半功倍的解题效果.
在整体操作中的应用
数学教学离不开实践活动的开展,而一节课的时间是有限的,用怎样的方式方法来提高活动效率是我们关注的问题[2]. 整体操作一般是指从宏观的视角来观察、分析与改造问题,将一些操作对象视为整体,在处理时以这个整体为单位进行处置.
遇到操作性的实践活动,教师首先要引导学生用集成的眼光来看待操作对象,操作时有意识地将一些具有相同属性的个体归在一个整体下. 在此过程中,学生需经历观察、猜想、思考、讨论、归纳、推理与反思等流程,结合自身原有的认知经验提出解决问题的办法.
例3 有7只杯口向上的茶杯摆在讲台上,现在请你们按照规则将它们的杯口全部倒扣在讲台上,规则是一次需翻转四只茶杯. 在这种情况下,能不能将所有的茶杯都倒扣在讲台上?若可以,需经过几轮翻转?证明你的结论.
学生看到本题的第一感觉就是要拿几个茶杯来试试,因为这是一个很容易操作的活动. 但是,在尝试过程中,学生发现翻转几次后就乱了顺序,感觉毫无头绪. 其实本题的答案是无法做到所有茶杯都倒扣在讲台上的,我们可以用赋值的方法来操作.
将正放的茶杯标记为“+1”,将倒扣的茶杯标记为“-1”,此时该活动就转变为七个“+1”轮流翻转成“-1”的活动. 每翻转一次,就有四个符号发生变化,最终想要得到的结果是所有的数都要变成“-1”,此时7个数的乘积也变为“-1”(将7个数的乘积看为一个整体).
想要让数字的符号发生变化,就是将这个数与“-1”相乘,每次翻转就有四个数与“-1”相乘,也就是乘以(-1)4=1,所以它们的乘积在翻动后是保持不变的. 初始阶段这七个数都是“+1”,经过n轮翻转后,它们的乘积依然保持为“+1”,所以永远不可能将这七个“+1”同时翻转成“-1”.
本题若依次嘗试,很难获得问题的结论. 而赋值法的应用,通过奇数和偶数规律的判别,问题的本质就水落石出了. 若杯子的总数为偶数,每次翻动一次的数量为奇数,也能用整体思想解题. 因此,整体思想的应用需多加琢磨,在应用中勤思考,达到触类旁通的目的.
在应用题中的应用
学困生有一个共同特点,看到题干较长的题目就畏缩不前,觉得自己肯定做不出来[3]. 而应用题一般都有比较长的文字描述,为了鼓励学生大胆向前,同时启发学生的数学思维,在解一些应用题时可利用整体思想化繁为简,直击问题的本质,起到出奇制胜的教学效果.
例4 李明、陈红和吴刚三个人是同班同学,李明和陈红分别从自家出发朝对方家步行,他们两家的距离为30km,李明的速度是2km/h,陈红的速度是1km/h. 吴刚则以5km/h的骑行速度往返于李明和陈红之间,若三人同时出发,至两人相遇,吴刚骑行的路程是多少千米?
本题待求的量是吴刚骑行的路程,首先要知道吴刚与其他两人中的一人相遇骑行的路程,再将各段路程加在一起就是待求距离. 此过程次数繁多,计算复杂,难免会出现纰漏. 从整体思想的角度去思考,只要从“路程=速度×时间”的公式着手即可.
吴刚的骑行速度是5km/h,他所骑行的时间就是李明与陈红相向而行至相遇所花费的时间. 列式为:30÷(2+1)=10h,5×10=50km. 从这个角度来思考,问题变得异常清晰,解题不再有什么障碍,因数据比较小且容易计算,更加不会因计算失误而导致错误的发生.
应用题主要是为了训练与考查学生的思维能力,整体思想在本题的应用,即实现了对问题的再创造,又有效地激发了学生的数学思维. 因此,整体思想的运用是解决应用题的法宝之一.
总之,整体思想在初中数学教学中的应用较多,这种数学思想对培养与发展学生的思维能力与思维品质具有深远的影响. 作为教师,应在教学的各个环节与各个章节有意识地渗透整体思想,潜移默化地引导学生,让学生在润物细无声中形成良好的数学思维,提高解题能力,为核心素养的形成奠定基础.
参考文献:
[1] 钱瑕玲. 中学数学思想方法[M]. 北京:北京师范大学出版社,2001.
[2] 林崇德. 学习与发展[M]. 北京:北京师范大学出版社,1999.
[3] 约翰·D. 布兰思福特.人是如何学习的[M]. 程可拉,孙亚玲,王旭卿,译. 上海:华东师范大学出版社,2013.

