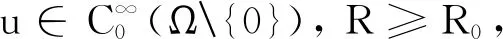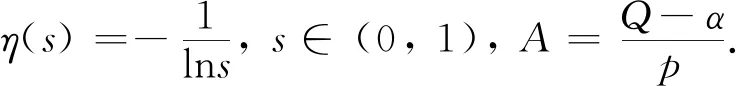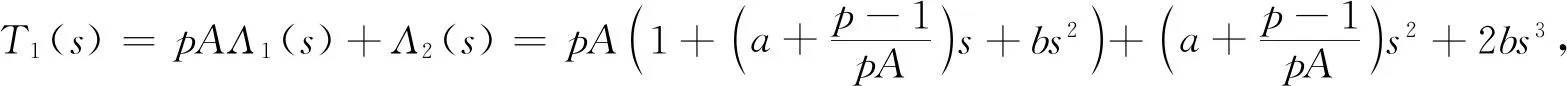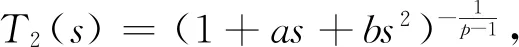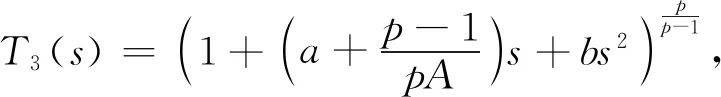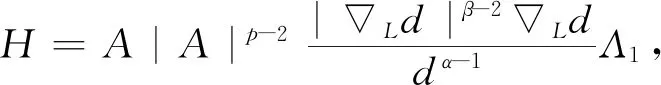广义HEISENBERG-GREINER p-退化椭圆算子的两类含权Hardy不等式
王胜军,韩亚洲
1.青海师范大学 数学与统计学院,西宁 810008;2.中国计量大学 理学院,杭州 310018
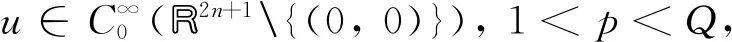
(1)
(2)
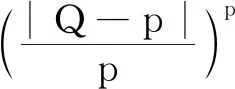
(3)
而且当2≤p 本文使用类似于文献[9]中的方法,利用散度定理,引入一类性质恰当的向量场,结合逼近的思想,推广了(1),(2)和(3)式,得到了广义Heisenberg-Greinerp-退化椭圆算子的两类含权Hardy不等式,进一步给出了最佳常数的证明. 广义Heisenberg-Greinerp-退化椭圆算子为一类具有高奇性的平方和退化椭圆算子[10],被更多的学者所关注,并得到了许多重要的成果[11-12].其构成向量场(见下文)Xj,Yj(j=1,2,…,n)在k>1时不满足Hörmander有限秩条件,从而它的亚椭圆性无法由此导出,增加了研究的难度[13-14].以下给出广义Heisenberg-Greinerp-退化椭圆算子的基本知识. 广义Heisenberg-Greinerp-退化椭圆算子形为 Lpu=divL(|Lu|p-2Lu) (4) 设ξ=(z,t)=(x,y,t)∈R2n+1,相应于(4)式中Lp的一个自然伸缩为 δτ(z,t)=(τz,τ2kt)τ>0 (5) 与伸缩(5)式相应的齐次维数是Q=2n+2k.由(5)式诱导的一个拟距离为 (6) 通过(6)式直接计算知道 (7) 另外,定义中心在{0}∈R2n+1,半径为R的拟开球为BR(ξ)={ξ∈R2n+1|d(ξ) 下的完备化,其中:Ω⊂R2n+1,1 (8) 当p≠Q,有 (9) (10) (11) 当0∈Ω,(8),(9),(10)和(11)式中的常数是最佳的. 证由(7)式直接计算得到 divL(d-a+1|Ld|b-2Ld)=(Q-a)d-a|Ld|b (12) 在Ω上,引入C1类向量场 divLH=divL(C|C|p-2d-(a-1)|Ld|b-2Ld)=p|C|pd-a|Ld|b |H|=|C|p-1d-a+1|Ld|b-1 这样就得到 (13) 也即 (14) 将(13)式代入(14)式的右边,利用(7)式得到(8)式. 在(8)式中,取a=2p,b=p得到(9)式;在(8)式中,取a=p,b=0得到(10)式;在(8)式中,取a=0,b=-p得到(11)式. 以下分两种情况证明(8)式中的常数是最佳的. 计算可以得到 从而有 进一步取ε→0,得到(8)式中的常数是最佳的,从而(9),(10)式及(11)式中的常数也是最佳的. 2)若Ω⊂R2n+1,已知(8)式中的常数可表示为 由于(8)式在(5)式的伸缩δR下不变,所以对于R>0,有 Cinf(BR(ξ))=Cinf(B1(ξ)) 因此,当BR(ξ)⊂Ω⊂R2n+1,有 |C|p=Cinf(R2n+1)≤Cinf(Ω)≤Cinf(BR(ξ))=Cinf(B1(ξ)) (15) Cinf(BR(ξ))=Cinf(B1(ξ)) 可得 Cinf(B1(ξ))≤Cinf(R2n+1) 结合(15)式,得到(8)式中的常数是最佳的,从而(9),(10)及(11)式中的常数也是最佳的. 注1在(8)式中取Ω=R2n+1,a=p,b=p时,得到(1)式,且p的取值范围较文献[5]中结果宽泛. 注2在(8)式中取a=p,b=p时,得到(2)式. (16) 特别地,在(16)式中取a=b=0,有下列带有余项的含权Hardy不等式 (17) 证为方便证明(16)式成立,首先令 从而当R足够大时,在Ω上有Λ0>0,Λ1>0. (18) (19) (20) 利用(18),(19)及(20)式,得到 (21) (22) 通过(21),(22)式,得到 (23) 又由于 也即 (24) 将(23)式代入(24)式,利用(7)式,得到(16)式. 注1在(17)式中取k=1,α=p,β=p时,得到(3)式.1 预备知识

2 一类含权Hardy不等式
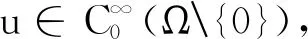
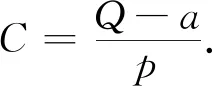
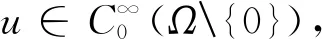
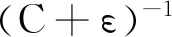
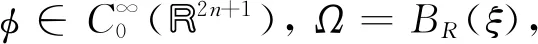
3 一类带有余项的含权Hardy不等式