Mn，Ce，Zn三掺铌酸锂晶体的电子结构和光学性质

刘林凤，张耘，邱晓燕，罗娅

西南大学 物理科学与技术学院，重庆 400715

随着现代信息技术的飞速发展，信息存储的高密化和高速化逐步成为必然要求．光学体全息存储技术因具有高存储密度、高冗余度、并行寻址和快速存取等诸多优点而成为新一代存储方案[1]．以优良光折变特性著称的铌酸锂晶体(LiNbO3，LN)是实现全息存储的首选材料之一．纯LiNbO3晶体在存取过程中信息易挥发，为此人们选择在LiNbO3晶体中掺入两种光折变离子使其禁带内形成两个光折变陷阱中心，进而在LiNbO3晶体中实现持久性全息存储．

在1998年，Buse等人[1]已经利用Fe和Mn双掺LiNbO3晶体实现了信息的非挥发性存储；Yue等人[2]在Mn和Ce双掺的存储实验中观察到明显的光致变色效应，这与双中心持久性数据存储有关；Kang等人[3]测量了Ce和Mn双掺LiNbO3的光伏常数和光电导率；Wang等人[4]分析了Li与Nb不同摩尔比的条件下Ce和Mn双掺LiNbO3晶体的光学性质．尽管Mn和Ce双掺LiNbO3晶体在存储时间和灵敏度等方面表现良好，但存在响应时间长、光致散射严重等不利影响，严重影响该材料的实际应用[5]，加入Zn或Mg等抗光损伤元素能有效改善这些问题[6]．实验上关于Mn和Ce，Mn和Fe双掺LiNbO3晶体的光学性质和存储的研究较为常见，但Mn和Ce双掺或Mn，Ce和Zn三掺晶体内部电荷迁移等机制(如杂质元素占位、电子跃迁机制)的研究鲜有报道．

本研究利用第一性原理，分别计算了Mn和Ce单掺、双掺及Mn，Ce和Zn三掺等多种掺杂LiNbO3体系的能带、电子结构以及吸收光谱，希望通过研究电荷跃迁机理，更好地为体全息存储器性能优化、参数设置等提供理论和数据支持．

1 晶体模型与计算方法

表1 LiNbO3晶体中各原子坐标

依据晶格参量、原子坐标建立了化学计量比的LiNbO3晶体2×2×1超胞模型．该模型共包含120个原子，其中Li原子、Nb原子及O原子的个数分别为24，24和72．本研究利用基于第一性原理的Cambridge Sequential Total Energy Package (CASTEP)软件包对模型进行优化和计算[8]．过程中采用广义梯度近似(generalized gradient approximation，GGA)中的PW91泛函和平面波超软赝势相结合的方法，电子间相互作用的交换-相关势由GGA进行修正，由于GGA考虑了空间点r处的电子密度及该处密度梯度，引入了非定域性和非均匀性，相较于利用局域密度近似(local-deasity approximation，LDA)方法处理，其结果更为精确[9-10]．多电子体系波函数通过平面波基矢组展开，为了尽可能减少平面波基矢数量，使电子轨道波函数在离子实内部的分布尽量平缓，采用超软赝势来描述离子实与价电子间的相互作用势[11]．计算中各原子的价电子组态分别选取：Li 2s1，O 2s22p4，Nb 4d45s1，Mn 3d54s2，Ce 4f15d16s2，Zn 3d104s2．

能量计算在倒易K空间中进行[12]，通过平面波截断能(Ecut)的选取来改变平面波基矢的数量，由此改变计算精度，同时运用快速傅里叶变换技术，使能量、作用力等计算在实空间和倒空间快速转换，进而保证计算的精确度和效率．计算过程中设置Ecut=400 eV[13]，对于电子结构和光学性质计算选取3×3×1的Monkhorst-Pack的特殊K矢对Brillouin区进行积分求和．所有模型在计算之前，都应对其结构进行优化．考虑到理论计算的需要与软件包的局限性，几何优化的收敛标准设置如下：自洽精度为每个原子2×10-6eV，原子间相互作用力不应大于0.5 eV/nm；晶体内应力为0.1 GPa，原子最大位移收敛标准为1×10-4nm，相关参量的取值与对应文献数据吻合[14]．几何优化过程中，当且仅当这些参量同时收敛时，迭代停止，优化结束．

在纯LiNbO3晶体中掺入两种光折变增强离子Mn2+和Ce4+，以及抗光折变增强离子Zn2+，在晶体中分别显示为 +2、+4、+2价[15-17]．对于掺杂LiNbO3晶体模型的构建，关键在于掺杂剂的占位．本研究中掺杂离子占位机制均基于LiNbO3晶体的本征缺陷结构为认同度最高的锂空位模型[6]．低浓掺杂情况下，+2价和+4价的离子进入晶格后优先占据Li位，并随之产生一定数量的锂空位来平衡电荷；当杂质离子浓度度较高时，它将同时取代晶格中的Li+和Nb5+，并形成相应电荷自补偿集团[6，18]．实际运用中，Mn2+和Ce4+的掺量一般都处于低浓度范围[1](摩尔分数小于1.00%)，故通过取代Li位方式进入晶格，同时产生相应数量的空位；在共掺时，Ce4+价态相对较高，较其他掺杂离子更易先占Nb位；掺杂离子同时占据Nb和Li位时，电荷平衡通过自补偿调节，减少晶体的畸变，晶体结构更稳定[19]．抗光折变Zn2+离子低于阈值摩尔分数(约7.00%)时占Li位，当达到7.00%还将进入Nb位．

将单掺Mn2+和Ce4+模型分别记为LNⅠ和LNⅡ；两者双掺记为LNⅢ；Mn2+和Ce4+加上小于阈值的Zn2+模型记为LNⅣ；三掺中Zn2+摩尔分数超过阈值模型记为LNⅤ．各掺杂样品的占位及电荷补偿形式见表2，所建立的超晶胞模型见图1．

表2 各掺杂样品的占位和电荷补偿

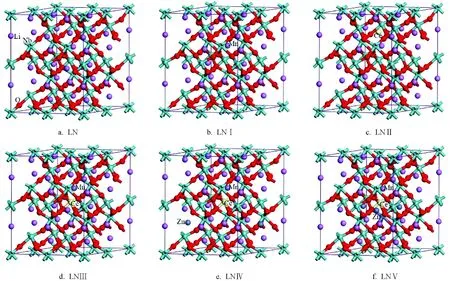
图1 各样本的晶胞模型

2 结果与讨论

2.1 晶体结构的优化

对各模型结构进行几何优化，表3列出了纯LiNbO3晶体晶格常数的实验值与优化结果[20]，两者的误差在2%左右，在模拟计算允许的误差范围内[21]，表明所建模型与晶体实际结构吻合较好．图2为各结构体系总能量随迭代次数的变化关系图，各体系总能量在优化进程中逐渐减小，最终都趋于定值，表明晶体结构处于稳定状态．表3和图2的结果表明该理论研究的模型基础、采用的计算方法、优化参数设置等均是合理的．

表3 纯LiNbO3 晶体常数优化结果与实验值

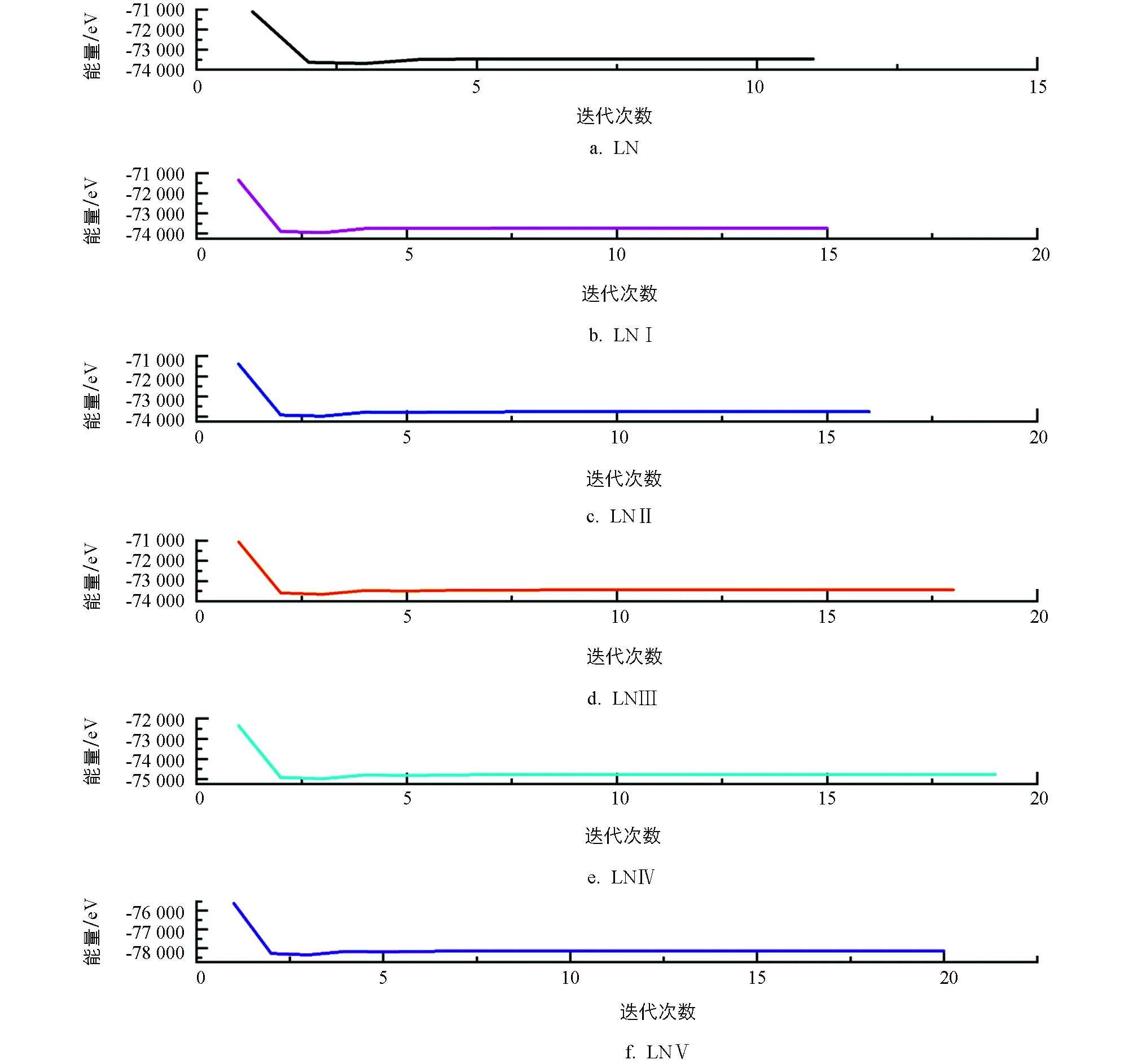
图2 各体系优化能量迭代情况

2.2 LiNbO3晶体及掺杂体系的电子结构

各体系的能带结构见图3．图3a显示纯LiNbO3晶体的禁带宽度为3.51 eV，该值与Xu等人[22]给出的计算值3.50 eV相当，较实验值3.78 eV[23]略低，但这并不会给我们对晶体电子结构的对比分析带来影响．掺杂使得晶体氧八面体结构畸变加大，内部对称性有所降低，各体系呈现不同程度的分裂．除单掺Ce4+的样本外，其余掺杂样本的能带结构均向低能方向移动且带隙宽度变窄．图3b和图3c显示，单掺Mn2+晶体和单掺Ce4+晶体在费米能级(定义0 eV为费米能级)附近出现几条较窄各自的缺陷能级．双掺Mn2+和Ce4+样本的带宽约为 3.06 eV(图3d)，其杂质能级主要分布在费米能级附近，数量有所增加．从图3e和图3f中可以观察到，与双掺样品相比，三掺体系禁带宽度进一步变窄，LNⅣ中带宽降至2.38 eV，LNⅣ带宽为2.66 eV；杂质能级位置有所变化．

电子态密度能够揭示晶体内部电子跃迁、原子轨道相互作用、成键情况等多方面信息．各模型禁带附近的态密度见图4．Li+的电子主要分布在远离禁带的-42 eV附近，该峰峰型尖锐，轨道局域性强，本研究不考虑掺杂对它的影响．从图4a可以看出，纯LiNbO3晶体的能带结构中导带部分几乎由Nb 4d轨道上的电子贡献；价带由O 2p和Nb 4d两轨道电子共同构成，两者轨道在-5～0.5 eV区间内能量接近，轨道间易发生杂化，据化学键成键理论[15]，两原子间以共价键连接．从图4b至图4e可以看出，在氧八面体的晶体场中Mn2+的3d轨道发生分裂，形成Eg和T2g两个轨道[20]．图4b LNⅠ样品中，费米能级主要由Mn2+的T2g轨道电子构成；Mn2+的3d轨道少量电子与O 2p以及Nb 4d轨道电子在-8～-2 eV区间交叠，形成共价键，共同组成价带，导带部分以Nb 4d轨道电子贡献为主，Mn2+的Eg轨道电子贡献为辅．相较图4a图，价带和导带能量均朝低能方向有所移动，与图3的能带结构图相对应．单掺Ce4+的LNⅡ样品中，O和Nb等元素对导带和价带的作用基本同纯LiNbO3样品一致；Ce 4f轨道的电子在2.6 eV附近形成一个尖锐且宽度较窄的峰形，说明Ce以离子键的形式存在于晶体中，另外6s和5d轨道电子(约在-33，-19～-13 eV)远离禁带，在光折变过程中不考虑这两轨道电子的影响．图4d双掺样品中，由于掺杂离子间的相互影响，晶体电荷自补偿，导致Ce4+进入晶体的占位较单掺时发生改变，其态密度峰向低能方向移动了3 eV 左右，使得该轨道与Mn2+的T2g轨道产生部分交叠，导带与价带组成成分与前几种样品相同．如图4e和图4f所示，当 Zn2+低于阈值或略高于阈值浓度，该离子在费米能级附近几乎没有贡献，其轨道电子主要集于-8～-2 eV之间，局域性较弱，与O 2p轨道杂化，表明Zn和O两者间具有共价性；受Zn2+影响Ce 4f 轨道发生分裂，形成4f1和4f2两个轨道．

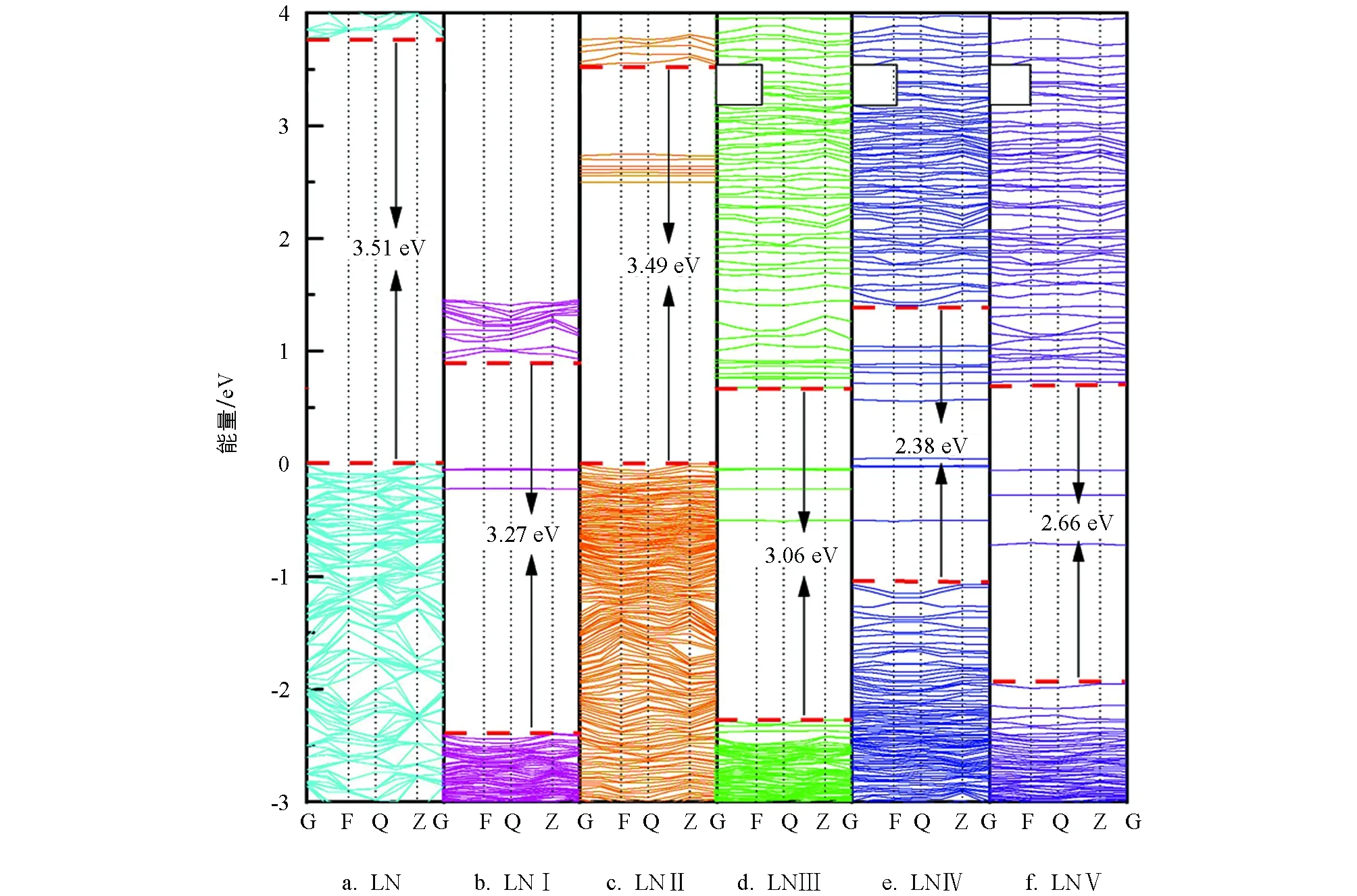
图3 各体系能带结构

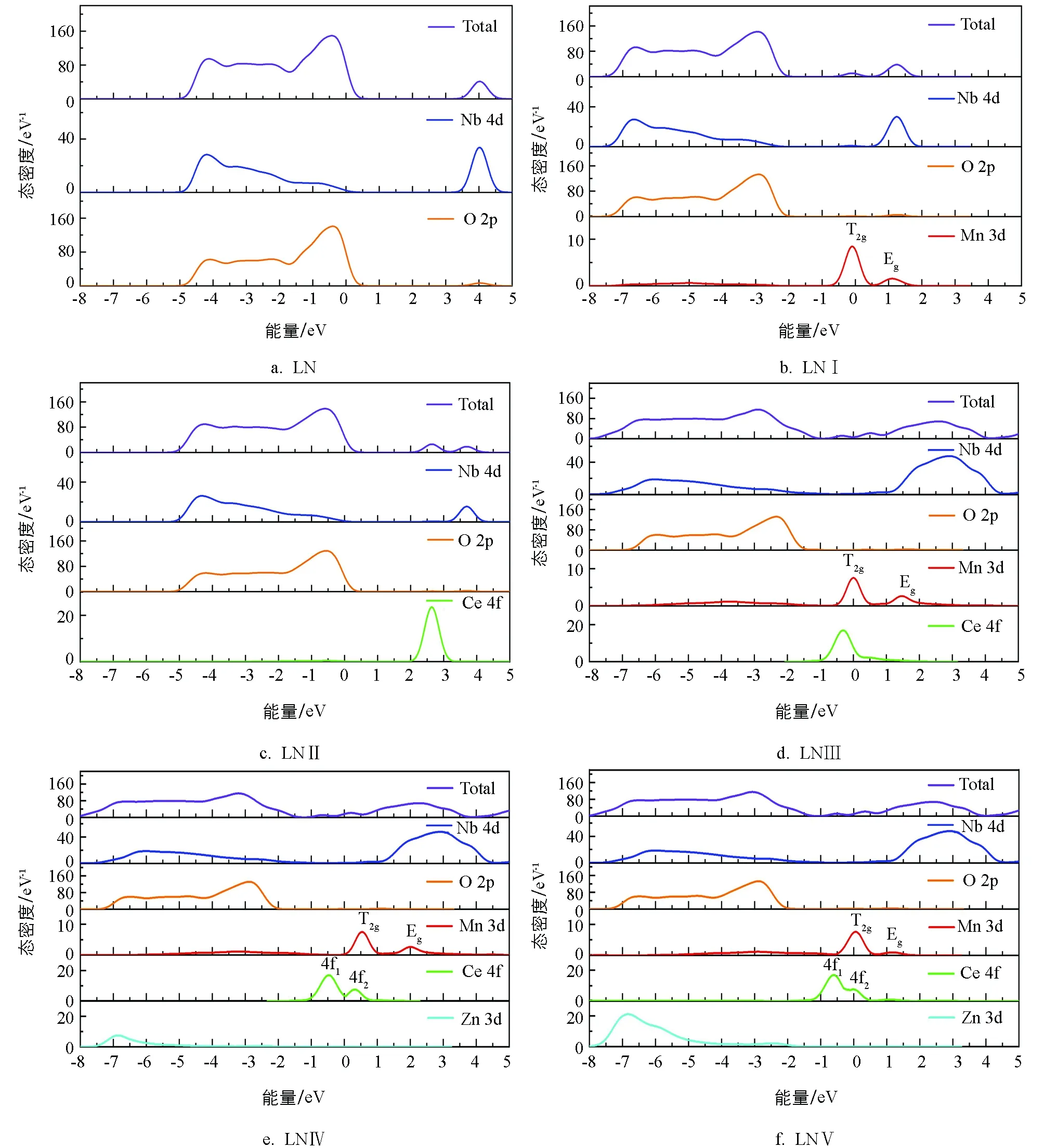
图4 各样本禁带附近态密度

2.3 LiNbO3晶体及掺杂体系的光学性质

固体物理中，线性响应范围内，晶体的光学特性主要是由频率的介电函数ε(ω)=ε1(ω)+iε2(ω)决定，其中ε1和ε2分别表示介电函数的实部与虚部，可由Kramers-Krönig色散关系推导得到[8，24]．晶体的折射率n和吸收系数α可以通过计算得到：

晶体光学特性计算基于优化模型，并利用0.27 eV的剪刀算符进行修正，使理论值与实验结果更相符．各样本在可见-近红外吸收光谱见图5．LiNbO3晶体的基础吸收边决定于电子从O 2P轨道向Nb 4d轨道转移跃迁所需的能量[18]，各掺杂体系吸收边较纯样本都表现出不同程度的红移现象．该现象与O原子电子云的形变密切相关，而其形变强弱取决于阳离子的极化能力，能力越大，周围O2-电子云发生变形越大，使得电子跃迁所需能量降低．阳离子极化能力大小可用有效荷电数(Z*)的平方与离子半径(r)的比值Z*2/r近似度量[18]，本研究涉及的阳离子极化能力从大到小顺序为Nb5+(58.51)、Mn2+(34.45)、Ce4+(32.88)、Zn2+(14.72)、Li+(2.49)，谱线中掺杂样本吸收红移均来自掺杂离子的极化能力高于原阳离子Li+；LNⅤ的吸收边较其他掺杂样本紫移，是由于掺杂离子占据了极化能力更高的Nb5+位．

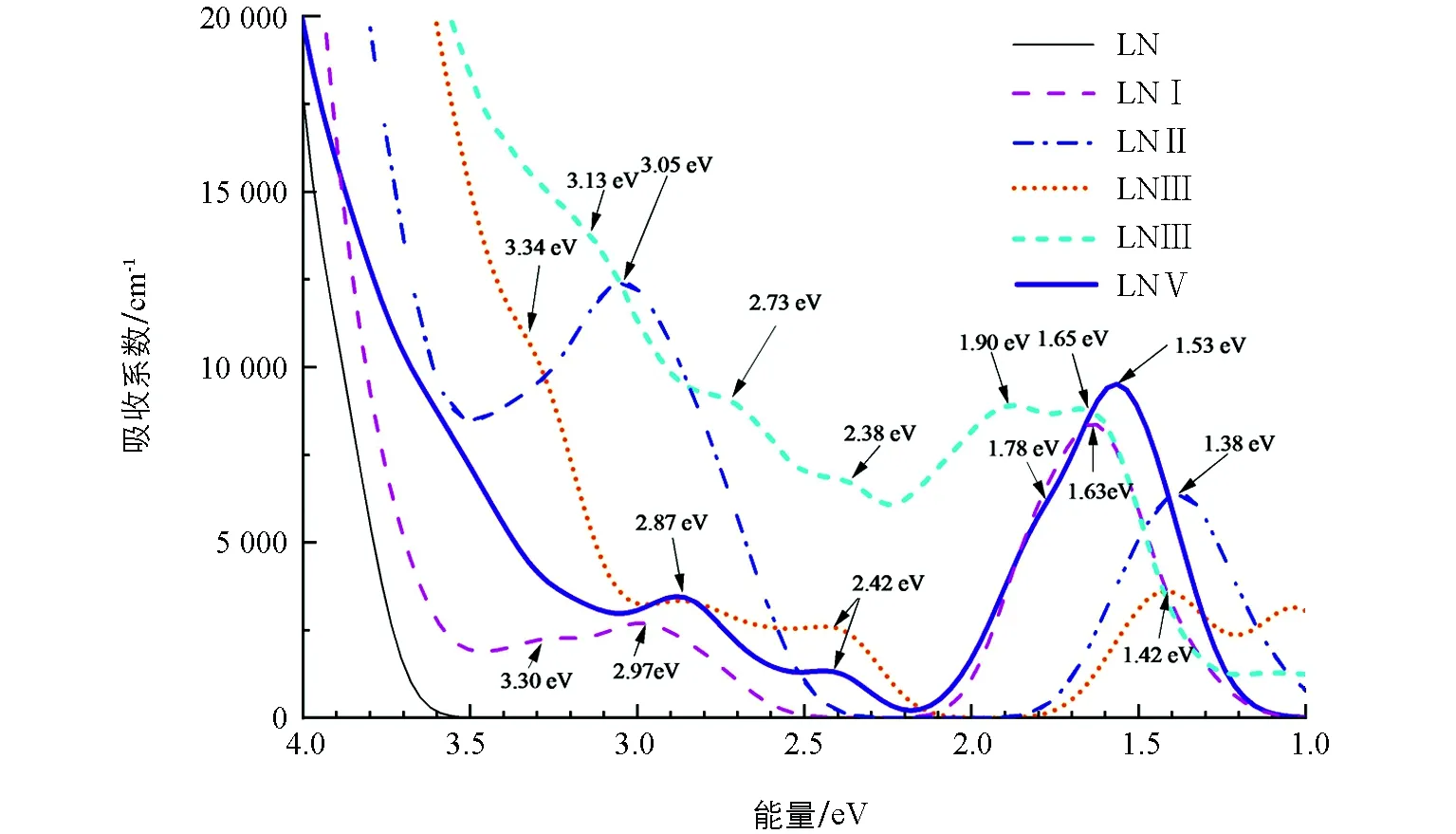
图5 各样本的可见近红外吸收光谱

由于纯晶体带宽为3.51 eV，大于可见光范围内的光子能量，故其在此区间没有产生光吸收．杂质的掺入使得晶体禁带间产生缺陷能级，在可见光区产生了明显的光吸收．

掺Mn2+的LNⅠ晶体分别在1.63 eV(760 nm)、2.97 eV(418 nm)以及3.30 eV(376 nm)处出现了吸收峰．文献[25]指出1.63 eV处的峰与本征缺陷小极化子吸收峰位置相符，推测其为晶体的本征缺陷结构引起．但考虑到计算结果中的以下因素：1.63 eV处的特征吸收出现在掺Mn2+后的晶体中，而纯样品中没有；结合态密度图4b，1.63 eV 峰对应Mn2+的T2g轨道电子向导带的跃迁，这里认为1.63 eV处的吸收与Mn2+相关．其余两处吸收峰(2.97 eV和3.30 eV)与电子从价带顶Mn2+轨道向导带的跃迁所需能量相吻合．波峰处于2.75～3.10 eV 区间且顶峰在2.97 eV左右的吸收峰，与报道给出的Mn2+缺陷能级深度2.80 eV左右较吻合[6，26]．顶峰位于3.30 eV的峰处于3.20～3.45 eV区间，此峰与应用中选取3.40 eV作门光束的存储实验相符[27]．

掺Ce4+的LNⅡ样本在3.05 eV(407 nm)及1.38 eV(898 nm)两处产生强吸收．前一个峰与报道给出的Ce4+在3.10 eV位置产生特征吸收高度吻合[18]，联系能级结构图3c和密度分布图4c，该峰形成于价带上的电子朝Ce 4f轨道的跃迁；1.38 eV处的吸收处于近红外波段，根据态密度图4c知道该峰是Ce 4f轨道电子向Nb 4d轨道跃迁的结果．

在Mn2+和Ce4+双掺样本LNⅢ中，由于杂质离子种类增加以及离子间相互作用，其吸收峰状态较单掺系统有所改变，在可见光-红外波段共出现4处吸收峰：3.34 eV(371 nm)，2.87 eV(432 nm)，2.42 eV(512 nm)，1.42 eV(873 nm)．通过与单掺样品对比及态密度图可知，前两峰归于Mn2+的特征吸收，较单掺样品吸收位略微偏移．2.87 eV 与Mn2+和Ce4+双掺实验中出现在2.76 eV(范围为2.70～2.93 eV)的吸收接近，该峰被证实与Mn2+有关[27]．结合态密度图4d，2.42 eV是电子由Ce轨道电子向导带跃迁的结果，但在Ce2+单掺LiNbO3样品中却没有出现2.42 eV附近的吸收；另外，Mn2+和Ce4+双掺相关实验证实此峰与Ce3+的特征吸收相关[18，28]；本文计算模型中，在单掺Ce4+、双掺Mn2+和Ce4+LiNbO3样品里Ce离子均以Ce4+的形式掺入．因此，有理由认为，双掺Mn2+和Ce4+LiNbO3样品中存在电子在两离子间的迁移：

Mn2++ Ce4+→ Mn3++ Ce3+

(3)

这就很好地解释了单掺Ce4+LiNbO3样品中1.38 eV 处的吸收峰在双掺样品中“消失”，而双掺Mn2+和Ce4+样品中出现单掺样品所没有的2.42 eV 附近的吸收峰．关于1.42 eV附近的吸收，对应电子从Mn T2g轨道Nb 4d 能级跃迁的结果，相比单掺Mn样品，位置略有移动，吸收强度有所下降．

在LNⅣ中，吸收峰数量和位置较双掺Mn2+和Ce4+LiNbO3样品均有所变化．3.13 eV(396 nm)、2.73 eV(454 nm)、2.38 eV(521 nm)的吸收峰较双掺体系向低能方向移动，而1.65 eV(752 nm)处的吸收峰则是向高能方向偏移的结果．该光谱中新增1.90 eV(653 nm)的吸收峰，由态密度图4e判断，此峰主要源于Ce轨道分裂形成的 4f2轨道电子向导带的跃迁．

当Zn2+浓度达到阈值时，对比LNⅣ样品，在LNⅤ中发现吸收曲线发生显著变化：3.13 eV 附近的峰不显现，这是由于受高掺Zn2+的影响，发生红移的吸收边与3.13 eV的弱峰相叠加，掩盖了此处不明显的吸收；样品吸收峰出现在2.87eV(432 nm)、2.42 eV(512 nm)、1.78 eV(697 nm)和1.53 eV(810 nm)附近．前两处的吸收与LNⅣ中2.73 eV和2.38 eV相比，半峰宽变窄，峰型更加凸显；2.42 eV与1.78 eV两峰分隔更明显，重叠部分大幅度减少，使2.42 eV的峰型锐利度增强；1.53 eV的吸收强度较双掺以及三掺体系(Zn摩尔分数未达到阈值)显著提高．

本研究的样品中，位于2.87 eV和2.42 eV左右的峰，分别对应Mn和Ce两功能性离子的吸收，在应用中常分别充当深、浅能级．与LNⅢ和LNⅣ样品比较，LNⅤ中2.87 eV 吸收峰峰形显现且相对突出，在用作全息存储中擦除光时，峰形的显现对确切波长的选取是十分重要的[29]．另外，在LNⅤ中，两峰间距较大，分隔更明显，可以避免使用2.42 eV对应的蓝绿光读取时对存储于深能级的信息造成破坏．

除了可以利用接近报道数据的深能级约2.87 eV和浅能级约2.42 eV外，2.42 eV(Ce)和1.53 eV(Mn)所对应的能级分别作为深、浅中心也是一种具有潜力的选择．从吸收谱看，LNⅤ中Mn2+在1.53 eV 附近具有强吸收特点，有利于信息的记录和读取．光栅衍射效率(η)是全息存储技术中重要的参量，定义为衍射光强与透射光强的比值．每张全息图的衍射效率可近似表示为[30-31]：

(4)

(5)

其中：τW表示记录时间常数，τe为擦除时间常数，M代表全息图数目，M/#代表动态范围，λ记录光波长，L是样品厚度，θ为布拉格角，Δn为折射率调制度，neff表示晶体有效折射率，γeff为有效电光系数．动态范围M/#和灵敏度S是双光全息存储的两个重要性能参量，结合(4)式可表示为

(6)

(7)

公式(6)和(7)表明，记录进程中，光吸收的强弱通过影响电荷的重新分布，进一步影响空间电荷场强弱、折射率调制大小等，最终影响衍射效率[26]．较强的光吸收，可提高空间电荷场ESC达到稳定状态的速度，减少记录时间，增加记录灵敏度并扩大动态范围．如选用810 nm(1.53 eV)的近红外光记录信息，LNⅤ样品对该波段的吸收更强，从而其动态范围和灵敏度均更佳．LNⅤ样品中，Mn 2.87Ce 2.42eV与Ce 2.42Mn 1.53eV两个组合均可用于双光全息存储，尤其后者在增加记录灵敏度并扩大动态范围上具有一定优势，而其运用还未见报道．

分析掺Ce4+的样品，有一个有意思的发现：单掺样品强可见光吸收为非光折变吸收(价带到Ce轨道的吸收)；与Mn2+双掺时，出现新的可利用的光折变吸收．尽管掺Ce4+不是经典的强光折变掺杂元素，在与其他离子双掺时却可能有新的吸收，来源于与其他离子间的电荷转移而形成的Ce3+．这里我们提出了Ce与Mn 之间存在电荷转移的观点，Ce4+与其他光折变离子间的电荷迁移情况有待证实．

3 结论

本文对纯LiNbO3晶体以及多种 Mn，Ce和Zn 掺杂LiNbO3晶体的电子结构、光学吸收谱进行了研究，掺Mn2+或Ce4+的LiNbO3晶体在禁带中形成杂质能级，分别主要由Mn 3d，Ce 4f 轨道电子提供．Ce4+在双掺样品中2.42 eV处产生的吸收对我们有所启示，在双光存储应用中一些掺杂离子，由于双掺离子的影响，可能表现出其单掺所无的光折变吸收，因而应用时应首先研究双掺时各离子的吸收特点．双光存储应用中，可选取Zn2+浓度达到阈值的LNⅤ样本中吸收峰Mn 2.87 eV，Ce 2.42 eV 或Ce 2.42 eV，Mn 1.53 eV两种情况，前者的记录光波长更短，记录的密度更高，后者记录光吸收强度更大，在衍射效率、灵敏度、动态范围等方面表现更出色．