考虑驾驶员特性的个性化跟驰控制策略研究

任玥，邹博文，尹旭，刘学高，梁新成

1.西南大学 工程技术学院，重庆 400715；2.西南大学 人工智能学院，重庆 400715；3.重庆长安汽车软件科技有限公司 智能控制室，重庆 401120

根据美国国家公路交通安全管理局(The National Highway Traffic Safe Administration，NHTSA)统计，超过90%的安全事故都是由于驾驶员失误造成的[1]．近年来，随着传感器的大范围普及和控制器算力的逐步提升，高级驾驶辅助系统(Advanced Driver Assistance System，ADAS)得到广泛应用．其中，自动紧急制动系统能够有效降低驾驶员负荷，减少因驾驶员疏忽导致的交通事故．以此功能为基础的车辆自主跟驰控制系统，也是车辆高度/完全自动驾驶系统的核心功能之一，对提高车辆安全性、舒适性、经济性有着重要的意义，近年来受到全球学者的关注和研究．

对于车辆跟驰控制，其主要基于自车和前方障碍的运动信息进行碰撞风险评估．目前较为成熟的风险评估模型包括以MAZDA模型、Berkley模型、NHTSA模型为代表的安全距离模型[2-4]和以碰撞时间(Time to collision，TTC)为代表的车间时距模型[5-6]．基于碰撞风险模型，Gerdes等[7]采用了一种基于多面滑模控制器对发动机输出扭矩和制动力矩进行控制，在跟车工况中，该方法能够精确地跟踪车辆期望速度并与前车保持合适的安全距离．Kim提出了一种新型的时变参数自适应速度控制器，其控制发动机和制动力矩跟踪车辆期望速度，该方法有着较高的跟踪精度并对于外界扰动有良好的鲁棒性[8]．模型预测控制策略(MPC)由于能够系统地处理全局约束，在跟驰控制中有着较好的效果．Li通过建立自适应巡航优化模型，平衡了在跟驰过程中车辆跟踪性能、燃油经济性和驾驶员期望响应的矛盾[9]．文献[10]采用高斯核函数描述了碰撞风险，并采用MPC控制器的优化目标，实现了车辆自适应巡航功能．

近年来随着人工智能和强化学习技术的快速发展，其越来越广泛地应用于决策和控制系统．罗颖等[11]采用深度确定性策略梯度(DDPG)算法，结合屏障控制方法，实现了车辆低速跟驰控制．朱冰等[12]考虑前车运动不确定性，采用基于PPO的深度强化学习方法，实现了车辆自主跟驰，并有效降低了在线计算量．虽然目前大多数跟驰控制策略已经更有效地避免碰撞，实现安全驾驶，但现有大多数控制策略是基于固定控制器参数的．而在实际驾驶中，由于不同驾驶员具有差异化的性格、驾驶技术、驾驶风格，而统一标定的控制策略无法满足不同驾驶员的驾驶习性，从而导致车辆自主跟驰功能的宜人性较差，乘员接受度低．管欣等[13]引入驾驶人模型并提出了基于驾驶人最优预瞄加速度模型的自适应巡航系统，实现了不同风格的跟驰控制．Yi等[14]通过采集实际驾驶人数据，采用基于具有遗传因子的递归最小二乘算法实现了驾驶人特性参数，并应用于自适应巡航的起停控制系统．文献[15-16]采用强化学习方法进行跟驰建模，并在学习过程中考虑了驾驶员行为特性．

为使得车辆自主跟驰功能能够满足不同驾驶员需求，文献[17-18]在进行安全距离建模时考虑了驾驶员行为特性．文献[19]将驾驶员数据进行聚类分析，并基于驾驶风格辨识设计了不同的ACC控制器参数，提高了ACC系统人性化．文献[20-21]采用逆强化学习方法，直接从驾驶员数据中拟合出决策算法，实现了拟人化的跟驰决策．

针对不同驾驶员的驾驶习性，基于模拟驾驶试验采集驾驶员真实驾驶数据和深度强化学习的车辆个性化自主跟驰控制算法进行研究，以期通过设置奖励函数满足车辆跟驰过程的安全性、舒适性和宜人性，并采用改进DDPG算法实现车辆加速度自适应控制．

1 驾驶员数据采集

相较于实车试验，模拟驾驶试验由于其具有高安全、低成本、多工况、可重复性的特点，被广泛应用于驾驶员驾驶数据的采集，本研究通过驾驶员在环虚拟仿真试验获取驾驶员跟驰行为数据．驾驶行为采集系统如图1所示．

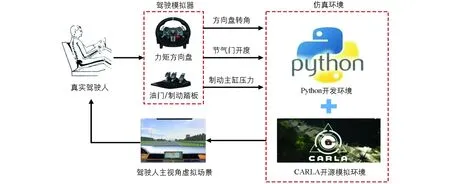
图1 驾驶行为采集系统

驾驶模拟试验在Ubuntu环境下进行．通过CARLA自动驾驶模拟器建立实时交通场景和环境车辆，采用罗技G29驾驶模拟器采集驾驶员方向盘转角、油门/制动踏板信号并传输到车辆动力学模型，输出主车实际运动状态，再与仿真场景实时交互．针对跟驰工况，本研究设计了前车匀速行驶、减速行驶、随机变速行驶等工况，以模拟城市环境的车辆跟驰典型工况．在模拟驾驶试验中，采集主车与前车的相对距离、相对车速、主车车速以及主车加速度序列作为驾驶员跟驰数据集．

2 个性化跟驰控制策略

2.1 车辆跟驰动力学建模

本研究中仅考虑车辆纵向运动，忽略车辆转向时侧向运动对纵向运动的耦合作用，建立车辆跟驰模型，如下式所示：

vh(k+1)=vh(k)+ah(k)ΔT

vr(k)=vl(k)-vh(k)

d(k+1)=d(k)+vr(k)ΔT

(1)

式中，vh和ah分别为主车车速和加速度，vl为前车车速，vr为相对车速，d为相对距离．ΔT为采样间隔．其中，主车加速度满足车辆纵向动力学方程：

(2)

其中，M为车辆质量，Ft，Fb分别为车辆的驱动/制动力．Ff，Fw，Fi，Fδ分别为车辆的滚动阻力、空气阻力、坡度阻力和加速阻力[22]．

在车辆跟驰控制过程中，选择主车车速、相对速度和相对距离作为状态空间，主车加速度作为动作空间，可表示为：

S=[vh，vr，d]

A=[ah]

(3)

在车辆实际运动过程中，其纵向加速度受到附着力限制，因此，为避免在学习过程产生不合理决策，设置动作空间取值范围为-6 m/s2≤ah≤6 m/s2．

2.2 奖励函数

在车辆跟驰过程中，不仅需要保证车辆的安全性，还需尽可能提高乘员舒适性．同时，还应使得跟驰控制策略更符合实际驾驶员行为特性，因此，车辆自主跟驰是一个多目标控制问题．在k时刻，定义速度跟踪奖励函数R1为：

R1=ω1(vh(k)-vd)2

(4)

其中vd为期望车速，由驾驶员启动自动跟驰功能时定义．

定义车辆跟踪奖励函数R2为：

R2=ω2ea·d(k)2

(5)

其中a为形状因子，表示为：

ρ为距离安全系数，以避免vr(k)为0时a无法计算[10]．

定义舒适性奖励函数R3为：

R3=ω3(ah(k)-ah(k-1))2

(6)

舒适性奖励函数旨在避免车辆在短时间内产生较大的加速度变化对乘员造成较大的冲击度从而导致的舒适性恶化．

定义个性化奖励函数R4为：

(7)

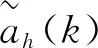
结合式(4)-(7)，在k时刻个性化跟驰控制策略奖励函数表示为：

(8)

其中dsafe为最小安全距离，vlim为道路最大限速，ωi为各项奖励的归一化权重系数．在训练过程中，当车辆发生不合理运动时(与前车碰撞、车速为负或超过限速)，给予智能体一个较大的惩罚．可以看出，奖励函数中权重系数ωi的取值直接决定了智能体的跟驰效果，在实际训练过程中，先通过调试ω1～ω3使车辆拥有较合理的客观跟驰效果，再调节ω4使得智能体决策结果能更与实际驾驶员特性更为接近．

2.3 基于TD3的跟驰控制策略

强化学习基于马尔科夫过程，通过状态、动作、奖励和状态转移函数描述智能体与环境的动态过程．作为一种试错学习方法，强化学习控制智能体选择不同动作，通过与环境不断地进行交互尝试，并通过环境给出的奖励来判断动作的优劣，最终学习到一个最优策略，使累计回报的期望最大化．

由于车辆跟驰行为是一个连续过程，对于传统的DQN(deep q-learning)、SARSA等算法需要将连续状态空间离散化，易造成维数灾难．深度确定性策略方法(deep deterministic policy gradient，DDPG)采用基于Actor-Critic框架，结合了DQN基于价值和策略梯度(policy gradient)基于策略的优势，通过对价值网络的时序差分更新与动作策略的梯度下降实现对连续动作空间问题的强化学习[24]．

DDPG中的actor网络为策略网络，表示为μ(s；θ)，其代表个性化跟驰控制策略．Critic网络为价值网络，表示为q(s，a；ω)，价值网络是动作价值函数Qπ(s，a)的近似，价值网络用于评价策略的好坏．动作价值函数可表示为：

Qπ(s，a)=E(Rk+1+γRk+2+γ2Rk+3+…|Sk=s，Ak=a)

(9)

其中γ为奖励衰减系数．

对于策略网络，将其输出的动作和当前状态作为价值网络的输入，此时价值网络可以表示为q[s，μ(a|s)；ω]，其值越高，说明策略越好，故定义策略网络目标函数为：

J(θ)=ES[q(s，μ(s；θ)；ω)]

(10)

gj=θq[s，μ(sj；θ)；ω]

(11)

θnew=θold+β·θμ(sj；θ)·aq(s，a；ω)

(12)

而对于价值网路，同样基于从经验回放数组中抽取的(sj，aj，rj，sj+1)，让价值网络通过历史数据和当前策略网络进行预测：

(13)

(14)

则TD目标可表示为：

(15)

定义价值网络损失函数为：

(16)

可通过梯度下降更新价值网络参数，如下式所示：

(17)

ωnew=ωold-α·ωL(ω)

(18)

对于式(15)和式(16)，TD目标是通过价值网络的估计进行计算的，而损失函数再次使用同样的价值网络对TD目标进行拟合，存在自举(Bootstrapping)的问题，容易导致对动作价值函数的高估或低估．为提升DDPG性能，使用TD3算法进行改进．此处采用两个价值网络和一个策略网络：

q(s，a；ω1)，q(s，a；ω2)，μ(s；θ)

(19)

再建立与3个网络对应的、并与各网络结构完全相同的目标网络：

(20)

采用目标策略网络计算动作，并添加噪声：

(21)

其中ξ表示策略网络噪声，并服从截断正态分布，其可以提高算法的鲁棒性，同时又可保证噪声不会过大．

将式(15)的TD目标重新定义为：

(22)

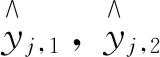
各神经网络间迭代关系如图2所示．

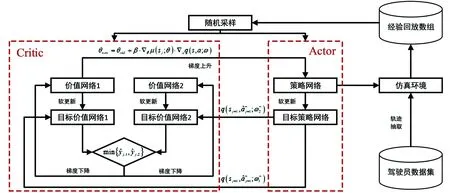
图2 基于TD3深度强化学习的网络结构

为确保价值网络对策略网路打分的可靠程度，减少策略网络的更新程度，在训练过程中，每一轮更新一次价值网络参数，间隔两轮更新一次策略网络参数．

基于TD3的个性化跟驰控制策略训练伪代码如表1所示．

表1 基于TD3的个性化跟驰控制策略伪代码

3 仿真与分析

为验证本研究提出的跟驰控制策略的有效性，并体现个性化程度，本节选取两种控制算法进行仿真对比，个性化跟驰控制策略训练方法如表1所示．未考虑驾驶员习性的跟驰控制策略采用同样的网络架构，也未考虑式(7)所示的奖励函数，训练过程中也未采用实际驾驶员数据．选择一段跟驰片段进行对比，仿真采样间隔为0.1 s．前车以18 km/h的初速度前进，随后进行先加速再减速的随机变速运动，前车车速变化如图3所示．

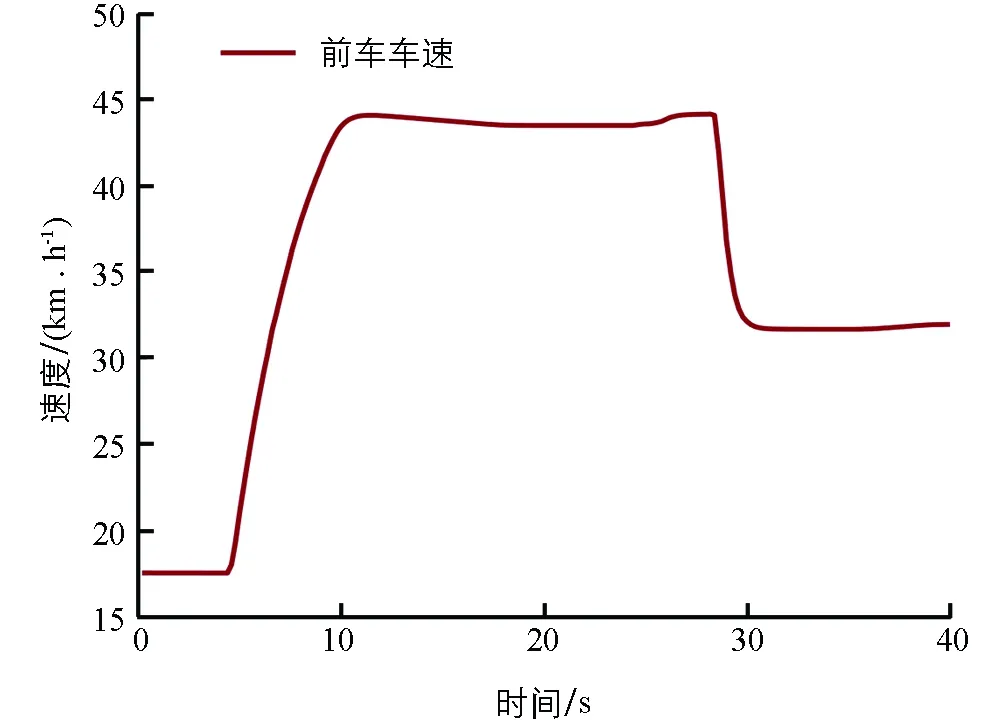
图3 前车车速变化

主车初始速度与前车同为18 km/h，两车初始相对距离为20 m，跟驰期望车速定义为60 km/h．两种跟驰控制策略的对比以及驾驶员实际驾驶数据如图4-图6所示．

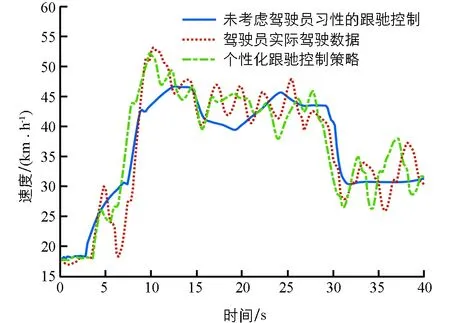
图4 主车跟驰速度对比结果

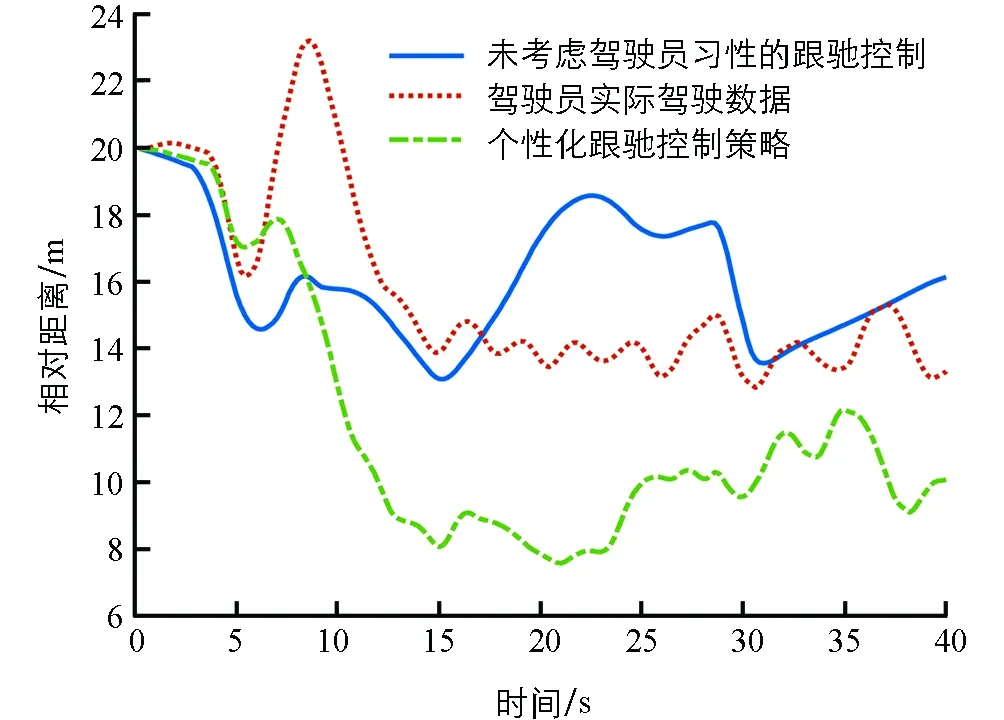
图5 跟驰相对距离对比结果

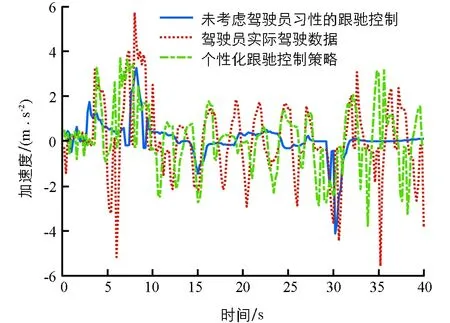
图6 主车加速度对比结果

图4-图6分别为跟驰过程中主车车速、相对距离以及加速度变化．可以看出，无论是否考虑驾驶员习性，基于深度强化学习的跟驰控制算法均能稳定、安全地实现自主跟驰功能．未考虑驾驶员习性的跟驰控制策略仅以客观跟随性、安全性和舒适性作为奖励函数，因此在整个跟驰过程中，无论是主车车速和加速度变化均较平稳．车辆加速度在大部分时间内维持在-1～1 m/s2之内，均方根值0.86 m/s2，最小跟驰距离为13.7 m．从实际驾驶数据可以看出，该驾驶员驾驶风格偏“激进”类型，在实际跟驰过程中，频繁加减速，导致车速波动较大，加速度变化也更频繁，车辆最大加速度绝对值达到5.6 m/s2，均方根值为1.73 m/s2，而整个跟驰过程的车辆相对距离也更近．当考虑了该驾驶员的驾驶习性后，本研究所提出的个性化跟驰控制策略相较未考虑驾驶员习性的跟驰控制策略更加 “激进”，车速波动和加速度波动更剧烈，和实际驾驶数据趋势更加接近，加速度均方根值为1.57 m/s2．另外，从相对距离可以看出，个性化跟驰控制策略的跟驰距离更近，最小跟驰距离达到了7.8 m．因此，本研究提出的自主跟驰控制策略通过驾驶员实际驾驶数据，实现了一定程度的个性化驾驶，相较基于客观目标奖励函数的跟驰控制策略，更能迎合驾驶员的驾驶习性和偏好．但从另一方面可以看出，由于本研究提出的个性化跟驰控制策略并未对驾驶员的驾驶技能专业程度进行评价，仅考虑了驾驶员的驾驶风格，因此实际决策结果与参考驾驶员驾驶的熟练度相关．当参考驾驶员的驾驶能力较差时，基于学习的决策难以使得车辆跟驰过程的平顺性、舒适性达到最优．

4 结论

本研究针对车辆自主跟驰过程中的宜人性问题，首先基于CARLA模拟器搭建了模拟驾驶试验平台，通过设计城市跟驰仿真场景，获取了驾驶员实际驾驶数据．然后建立了车辆跟驰动力学模型，并综合考虑车辆跟驰过程的安全性、舒适性、跟随性和驾驶员习性，设计了相应的奖励函数．最后结合驾驶员试驾数据，采用了改进DDPG算法对自主跟驰控制策略进行了训练．仿真结果表明，本研究提出的个性化跟驰控制策略能够实现稳定、安全地车辆跟驰控制．同时，通过在奖励函数中添加驾驶员偏好特性，能够有效地提高自主跟驰控制的个性化程度，使得决策结果更倾向于驾驶员的驾驶行为特性．