基于NSGA-Ⅲ算法的泳池式低温供热堆最优临界棒位搜索方法

胡彬和，刘兴民，孙 征，柯国土

(中国原子能科学研究院，北京 102413)

中国原子能科学研究院于2016年开始400 MW“燕龙”泳池式低温供热堆的研发工作，该方案将堆芯放在足够深的水池底部，利用水层的静压力提高堆芯出口水温(～100 ℃)，从而使向热网供水的温度(～90 ℃)达到热网需求[1]。2017年在49-2游泳池式反应堆(简称49-2堆)上进行了供热演示，验证了49-2堆用于城市低温供热的固有安全性[2]。但49-2堆作为研究堆其热工参数较低，对热工设计要求不高。“燕龙”泳池式低温供热堆为取得较好的经济性，其热工参数相对较高，对热点因子和焓升因子限值要求较为严格[3]。

“燕龙”泳池式低温供热堆为无硼控堆芯，堆芯的主要反应性控制手段仅能依靠可燃毒物和控制棒束。为提高堆芯组件平均卸料燃耗，尽管采用了多批换料制，但仍有较大的剩余反应性需由多组控制棒束调节，因此循环初(BOC)控制棒束插入堆芯较深，引起堆芯功率畸变，对稳态热工极为不利，故而进行最优临界棒位搜索以降低热点因子和焓升因子十分重要。本文探讨使用多目标优化遗传算法NSGA-Ⅲ实现无硼控堆芯最优临界棒位搜索的一般方法。

1 数学模型和算法设计

以“燕龙”泳池式低温供热堆为例，堆芯装载69盒CF3S燃料组件，布置57束控制棒束，其中首炉循环以C4、C7、C8为燃耗补偿棒束，控制棒行程210 cm，控制棒步长1 cm。

1.1 问题的抽象模型

考虑反应堆堆芯有n个控制棒组作为燃耗补偿棒，第i个棒组的控制棒位置为xi，则各棒组的控制棒位置可用向量x=(x1,x2,…,xn)表示。针对每个x=(x1,x2,…,xn)进行堆芯三维计算，可得到临界偏离度(y1，定义为|keff(x)-1|)、核焓升因子(y2)、核热点因子(y3)。已知有效增殖因数数值上不会超过平均裂变中子数[4](热中子堆一般为2.45)，核焓升因子和核热点因子均大于1.0。取临界偏离度|keff(x)-1|为目标函数之一是因为只有在临界状态附近计算所得的核焓升因子和核热点因子才具有实际意义，同时该目标函数可自然地归结到极小值问题。

需保证在临界状态附近，在核焓升因子和核热点因子满足热工限值的条件下，使核焓升因子和核热点因子尽量取得极小值。因此，可将其归纳为如下数学问题：

已知x=(x1,x2,…,xn)，且

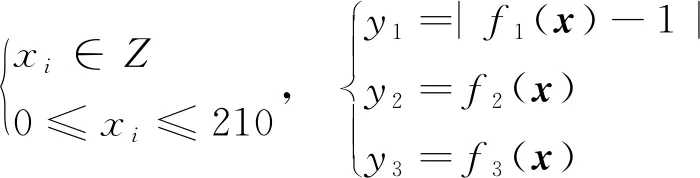
上述3个目标函数表达式未知，但由相应输入可算得其具体函数值。目标函数值域如下：

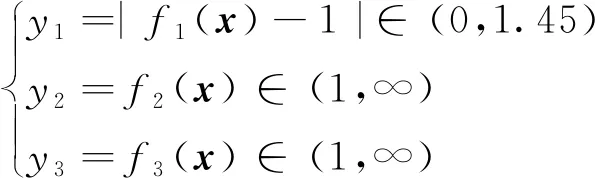
求：搜索x=(x1,x2,…,xn)使y1、y2和y3取得极小值。

这是一个无约束多目标优化问题，一般的遗传算法只能解决单目标优化问题[5]。在多目标优化问题中，各目标之间相互制约，可能使得一个目标性能的改善往往是以损失其他目标性能为代价，很可能不存在一个使所有目标性能都达到最优的解。在众多的多目标优化遗传算法中，NSGA-Ⅲ算法因其优越性是应用最广泛的一种算法，目前已成为多目标优化问题中的基本算法之一[6-7]。

1.2 算法具体实现

NSGA-Ⅲ算法的具体实现过程如下。

1) 生成初始种群：随机生成个体x=(x1,x2,…,xn)(即每个堆芯三维计算case的棒组棒位，xi取值范围为[0，210])，种群大小为N。

2) 计算目标函数值：对种群的每个个体进行堆芯三维计算，获得|keff-1|、Fdh、FQ3个目标函数值。

3) 目标函数值惩罚：偏离临界状态过远，即使焓升因子和热点因子均能取得极小值，也应在下一代种群中以较大的概率将其舍弃。为此提出附加惩罚函数：当个体的临界偏离度超过10-2时，该个体的核焓升因子和核热点因子均分别额外加上当代种群所有个体的核焓升因子和核热点因子的标准差，以使这些个体以更大的概率在下一代种群中被舍弃。

4) 交叉和变异：交叉算符选择模拟二值交叉(SBX)，模拟二值交叉综合了二进制编码和实数编码的优势，可在实数编码上模拟二进制编码的搜索特点。变异算符选择多项式变异。

5) 快速非支配排序：经过交叉和变异产生子代种群后，合并父代和子代种群，采用快速非支配排序算法[8]对合并种群进行分层，选出前Fl层最优个体。

6) 自适应归一化：由于需将每个解和参考点相互联系从而维持多样性，参考点又是均匀分布在目标空间中的[9]，而每个解的各目标函数值尺度不同，导致解的偏向性不同，那么在联系解和参考点时，各目标函数的作用就会不“公平”，因此需对目标函数值进行自适应归一化[6]。

7) 联系个体和参考点：建立个体到参考点联系，根据最小生境数选择剩余个体，并与之前选择的前Fl层个体共同组成新一代种群(种群大小为N)，重复上述过程直至达到收敛代数。最后得到1个优化搜索解集。

算法流程如图1所示。另外，针对算法中最为耗时的堆芯三维计算，设计了并行计算程序[10]。

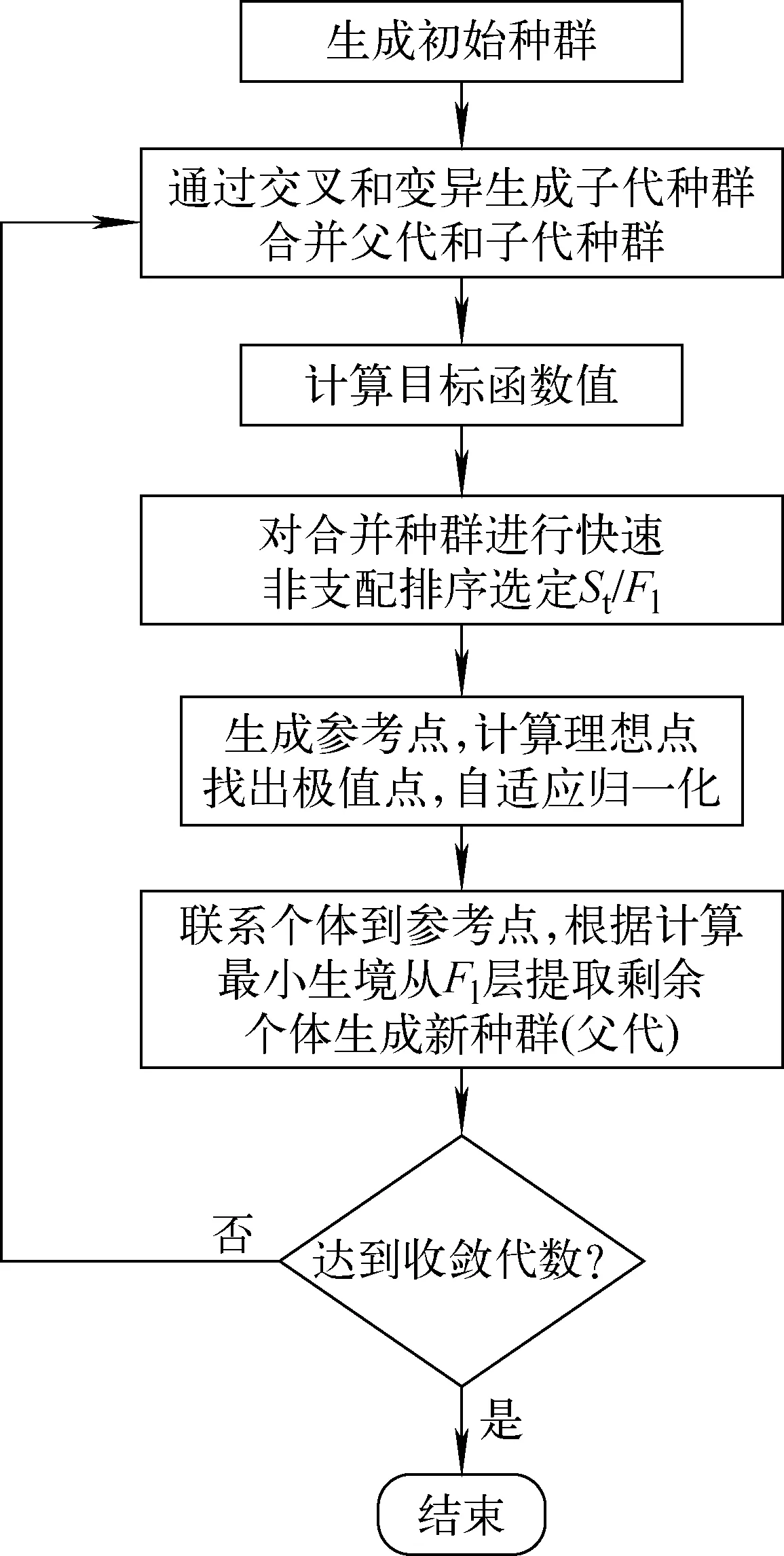
图1 NSGA-Ⅲ算法流程图Fig.1 Algorithm flow chart for NSGA-Ⅲ

2 算例分析和验证

“燕龙”泳池式低温供热堆辽源示范工程69盒CF3S组件400 MW堆芯方案已完成了从首炉循环到平衡循环的堆芯初步核设计。相关计算表明该方案能满足热工和安全设计准则，且具有较大的设计余量。为验证NSGA-Ⅲ算法在最优临界棒位搜索中的有效性，针对该方案的首炉堆芯进行算法验证。

为展平功率并提高平均卸料燃耗，首炉堆芯按组件富集度分3区装载，采用外内式的装载方案和3批换料制[11]，装载方案如图2所示。全堆布置控制棒57束，其中8束紧急停堆棒束(C5、C6)组成第2停堆系统；调节棒束和补偿棒束组成第1停堆系统，其中1束调节棒束(C0)作为调节棒组；其余48束控制棒作为燃耗和功率补偿棒束，如图3所示。其中C4、C7、C8作为首循环的燃耗补偿棒。

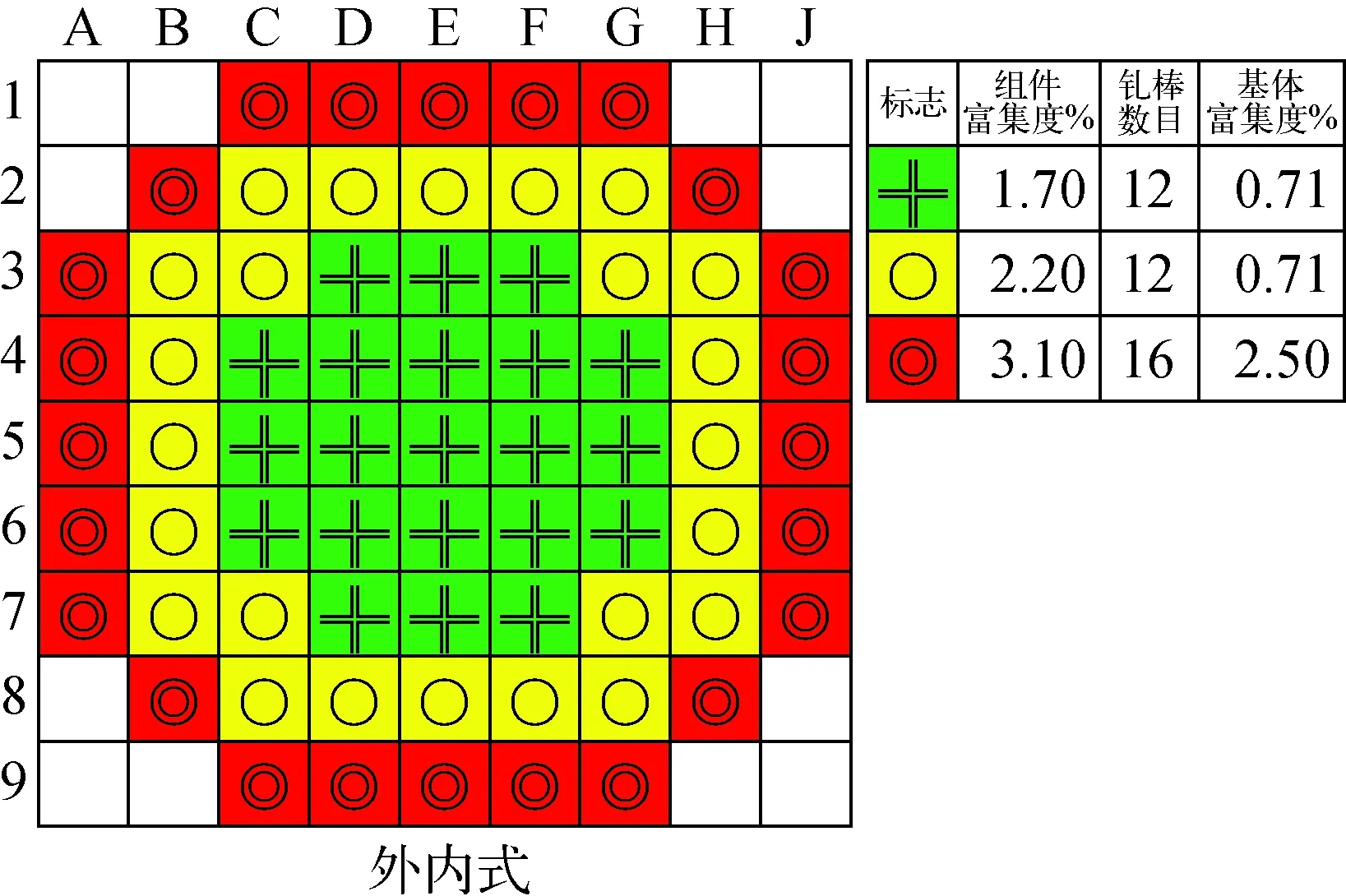
图2 供热堆首炉堆芯装载Fig.2 Load pattern of the first cycle for heating reactor

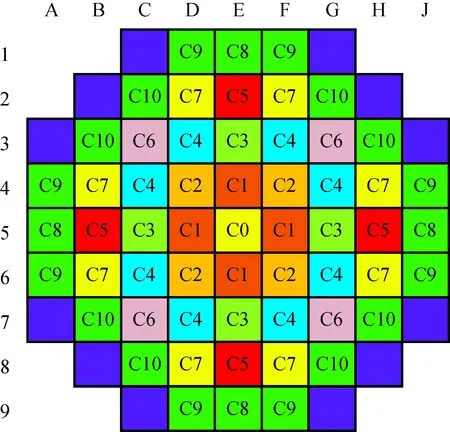
图3 辽源泳池式低温供热堆堆芯控制棒组布置Fig.3 Layout of control rod cluster for Liaoyuan pool-type low temperature heating reactor core

在采用最优临界棒位搜索算法之前，堆芯循环初的临界棒位是依靠人工手动尝试搜索的。经过大量人工手动尝试和修正，得到首炉堆芯450个等效满功率天(EFPD)各燃耗步的临界棒位如图4所示。

由图4可见，循环初手动搜索到的符合设计要求的临界棒位为[0，100，32]，依次对应的控制棒组为C4、C7、C8。相应的有关热工参数列于表1。

由表1可见，在循环初热态满功率零燃耗临界棒位状态下，堆芯的焓升因子为1.567，热点因子为3.477，均能满足热工和安全设计要求。

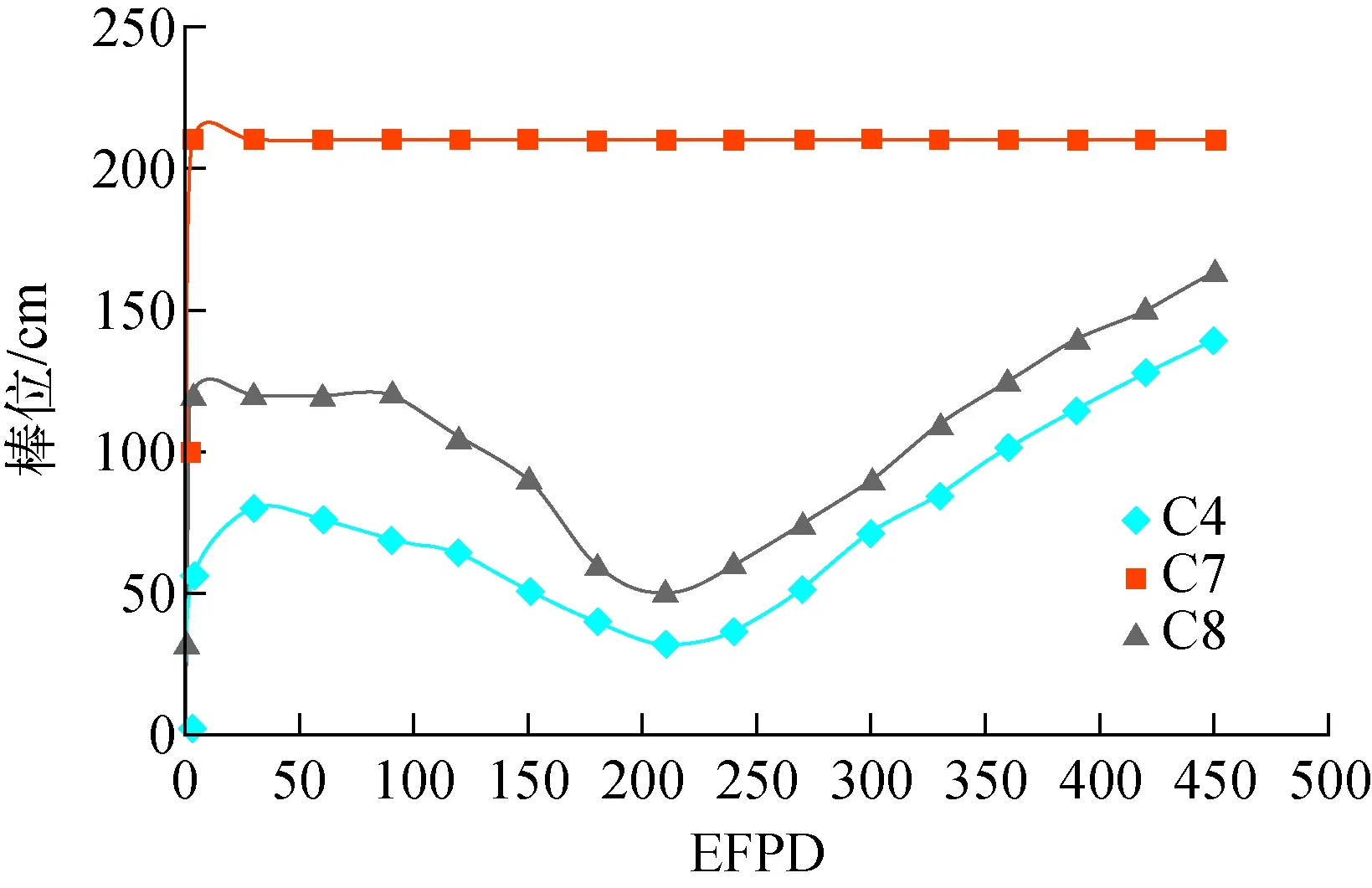
图4 辽源泳池式低温供热堆首循环提棒顺序Fig.4 Rod withdraw sequence of the first cycle for Liaoyuan pool-type low temperature heating reactor

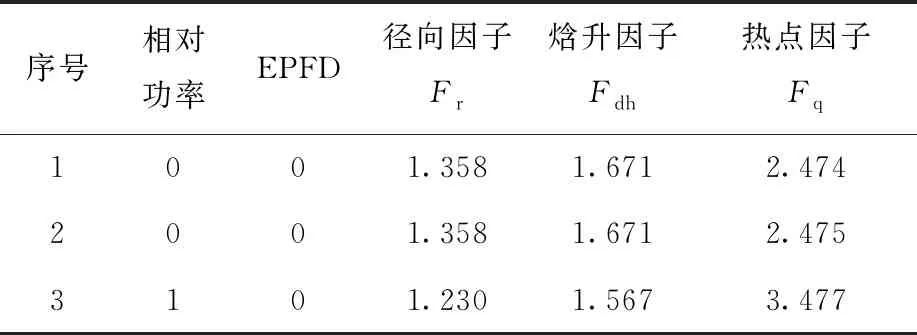
表1 69盒400 MW堆芯方案首炉循环初热工因子Table 1 Thermal factor at BOC in first cycle for 400 MW-69 assemblies core scheme

采用NSGA-Ⅲ算法对循环初热态满功率零燃耗状态下进行最优临界棒位搜索，设置种群数为200，遗传代数为100代，变异概率为10%，交叉和变异参数均设为20，并采用目标函数值惩罚策略，最终得到第1代和第100代的优化结果列于表2、3。

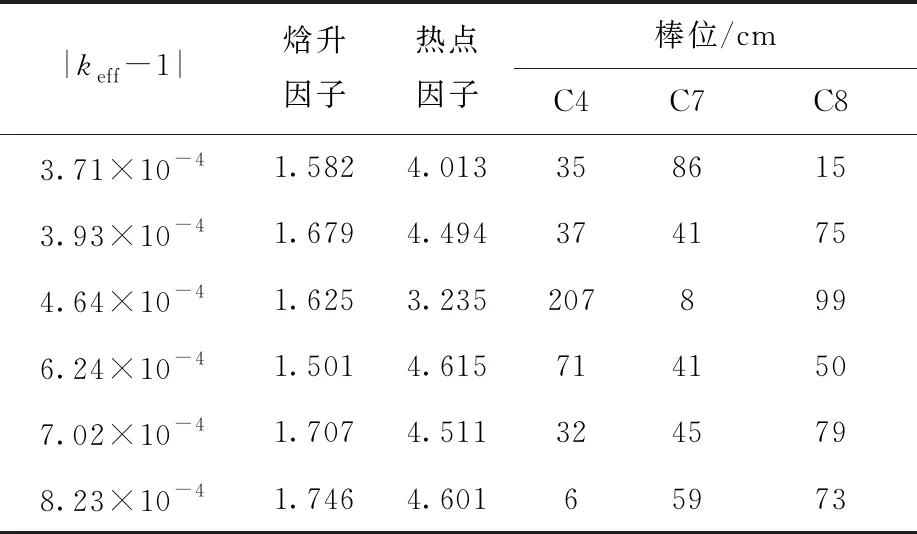
表2 初始种群Table 2 Initial population

由上述第1代和第100代的优秀种群个体列表可看出，第1代随机产生的控制棒组棒位没有1个解可满足热工和安全设计要求，而采用NSGA-Ⅲ算法经过100代种群迭代以后，产生了4个能满足设计要求的解，并且这4个解中有两对均趋向于同一种解，显示了NSGA-Ⅲ算法较强的搜索能力。同时可看到，优化解之一[0，99，34]非常接近手动搜索的解[0，100，32]，自然给出的核焓升因子和核热点因子[1.562，3.500]也与手动搜索解[1.567，3.477]非常接近。

表3 经过100代后的优化解集Table 3 Optional solution set after 100 generations

在计算效率上，人工手动尝试和修正所耗费时间无法准确估计，但基本以天计。而上述算例(200个体×100代)在16核32线程计算机上使用NSGA-Ⅲ算法搜索仅需3 h即能得到优化解集(多个解)，并且随着问题规模的增大，优化搜索算法的优势会更加明显。

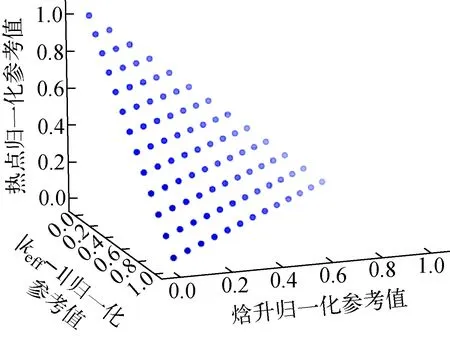
图5 一致性参考点分布Fig.5 Distribution of reference point

图5为归一化目标函数参考点(又称一致性参考点)分布，其分布非常均匀，保证了搜索空间的广泛性和均匀性。图6为第100代优化解集的种群个体分布。

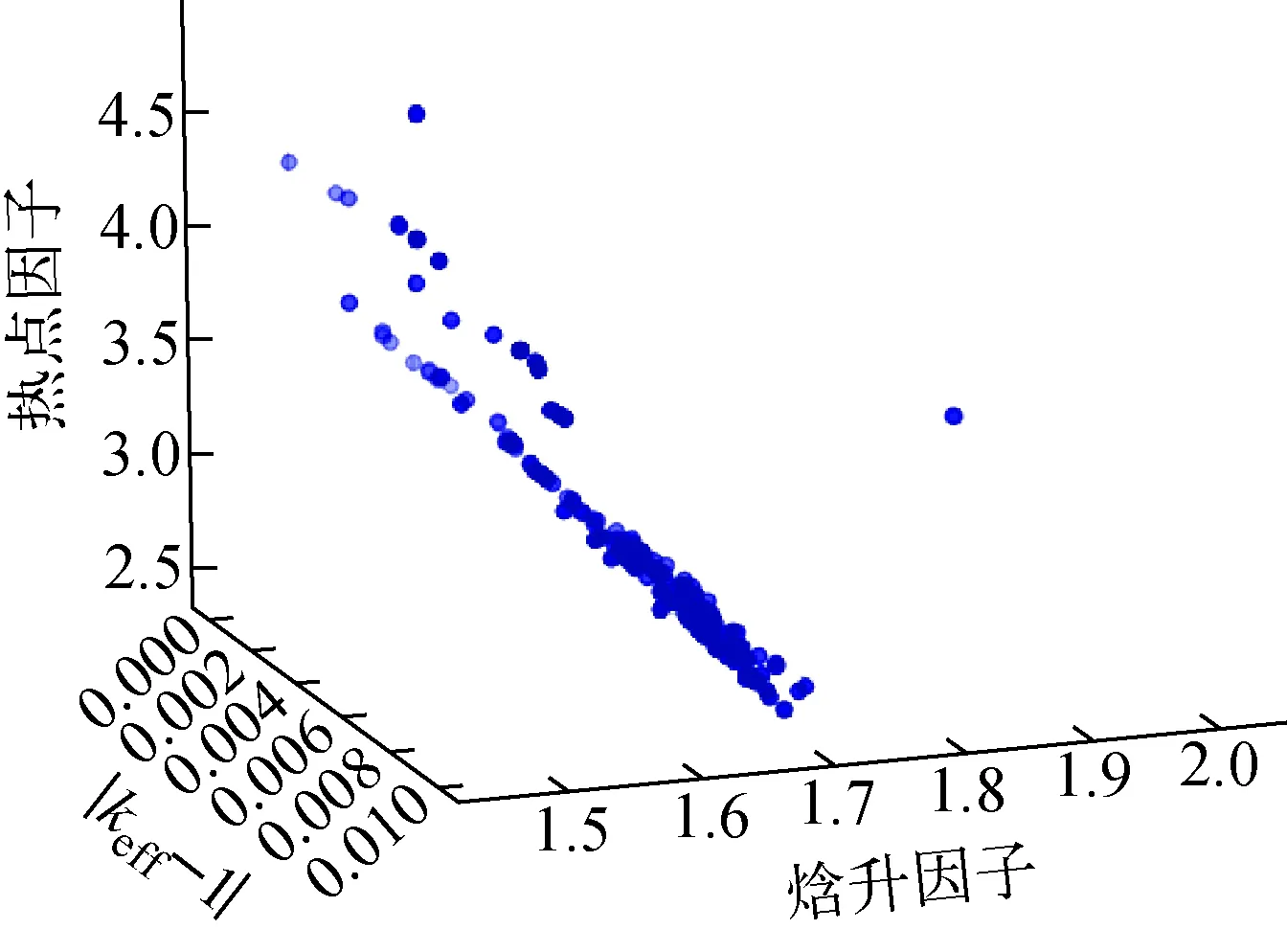
图6 第100代后的优化解集Fig.6 Optional solution set after 100 generations

为检验上述搜索结果是否具有随机性，增加了一次优化搜索，其第1代和第100代的搜索结果分别列于表4、5。

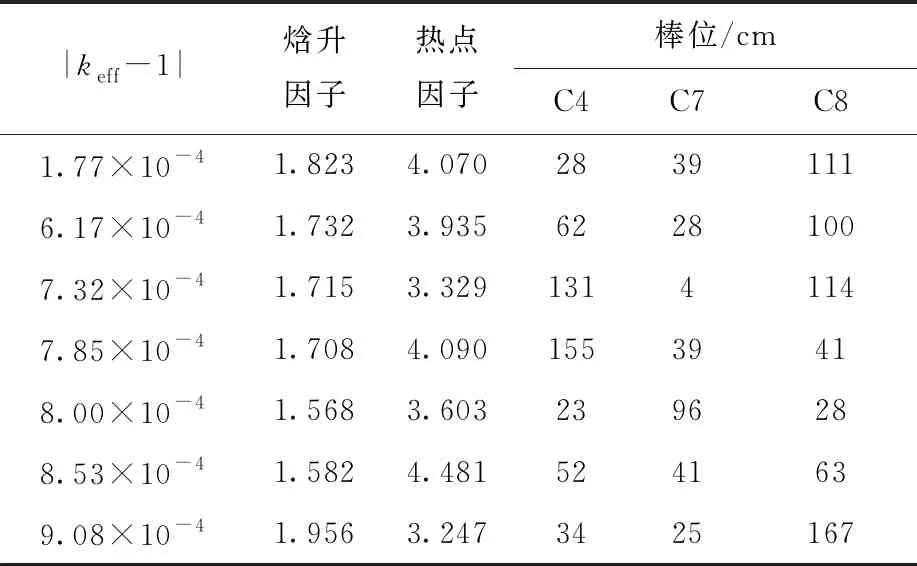
表4 第1代随机产生的初始种群及其目标函数值Table 4 Initial population and its target function value randomly generated by the first generation

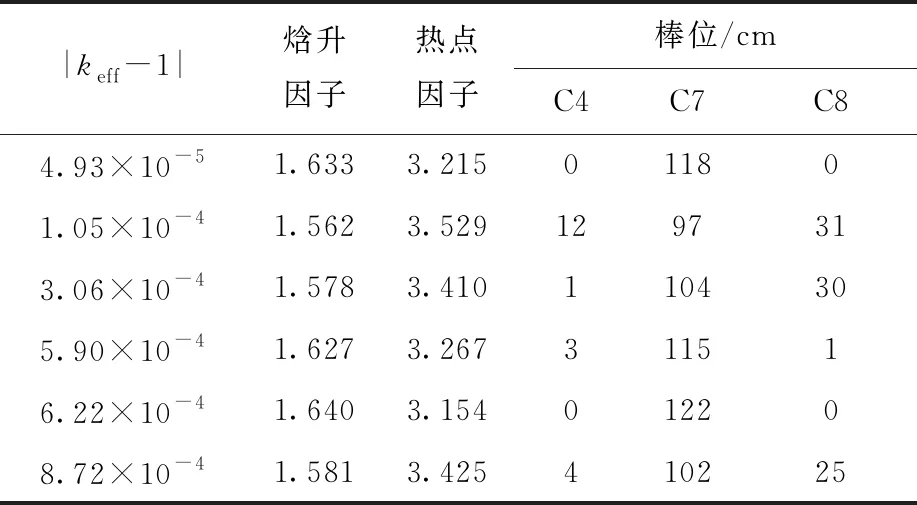
表5 第100代生成的种群中占优的个体及其目标值Table 5 The 100th generation population pareto point and its target value

由表4、5可见，在第1代中随机生成了1个较好的满足热工要求的解。经过100代种群迭代后，仍搜索到与第1次搜索十分接近的结果，表明NSGA-Ⅲ算法具有较强的收敛性，证明了其优化解的搜索能力不是随机的。同时，也证明了该算法对于保留和改善初始较优解的能力。

3 结论

采用NSGA-Ⅲ算法解决了“燕龙”泳池式低温供热堆最优临界棒位搜索问题，并通过“燕龙”泳池式低温供热堆首循环算例验证了算法的有效性，为泳池式低温供热堆提供了完全基于数学过程的搜索方法，该方法可推广到无硼控堆芯最优临界棒位搜索。