BCC 点阵结构力学性能与应用

张璠, 田国富

2001 年， 美国哈佛大学的Hutchinson 教授首次[1]提出点阵结构的概念， 是由杆件在空间上的结点与结点间的连接组成， 按一定规则重复排列，也常被视作微桁架结构。

随着3D 打印技术的成熟， 点阵结构制备的复杂程度和成本大大降低。 同时， 由于点阵结构具有轻质、 减震、 吸能和传热渗透等功能特性[2]，在航空航天、 机械、 医疗、 汽车等行业应用广泛[3～5]。

本文研究点阵结构中最为经典的BCC 点阵结构， 分析其力学性能， 并应用在轻量化设计中，证明点阵结构在轻量化设计中有明显优势。

1 BCC 点阵结构模型与参数

1.1 BCC 点阵单胞的结构

BCC 点阵结构模型中的每个单胞模型由8 根横截面为圆形的杆件组成， 各杆件在中心点相交且长度相同， 每根杆件长度为l， 单胞底边为正方形， 底边长为l1， 单胞的侧边长为l2， 杆件的半径为r， 直径为d， 杆件与底面夹角为θ（ 见图1、 图2）。

图1 BCC 点阵结构单胞模型示意图

图2 BCC 点阵结构

1.2 BCC 点阵结构的相对密度

相对密度用来描述材料的轻质化程度， 也是影响点阵结构力学性能的关键因素之一。 由于点阵结构的结构特殊性， 以及整体结构是由点阵单胞在空间上呈周期性排列分布组成的， 整体结构的相对密度可由单胞的相对密度得到， 所以取单胞的相对密度进行分析。

根据点阵结构的几何参数可得到杆长为：

同时， 根据相对密度的定义可以得到BCC 点阵结构单胞的相对密度为：

2 BCC 点阵结构的等效弹性模量

弹性模量是工程材料重要的性能参数， 负责衡量物体抵抗变形能力， 也是研究材料力学性能的重要指标。 因此， 将点阵结构视为一种材料并研究其等效弹性模量对研究其力学性能十分重要。

为了研究静态力学性能， 参考文献[6] 引入以下假设：

（1） 对制备点阵结构的材料要求连续性、 各向同一性及均匀性。

（2） 组成点阵结构的杆件横截面为圆形。

（3） 点阵结构单胞中所有杆件都属于细长杆。

（4） 当有外部载荷作用时， 各杆件只发生微小变形。

当点阵结构在竖直方向上受到载荷时， 每个杆件承受的压力为Pr， 四个杆件的均分压力载荷为P（见图3）， P=4Pr。

图3 BCC 杆件受力示意图

取其中一个单一胞体中的杆件进行静力学分析， 由于点阵结构具有对称性， 故对点阵结构受力模型进行简化， Pr从顶端点移至B 点产生的弯矩为：

根据得到的结果可知， 点阵结构的等效弹性模量与杆件的半径成正比， 与杆件长度成反比， 即杆件半径越大， 杆件长度越小， 点阵结构的承载能力越强。

3 在轻量化设计中的应用

笔者以典型连杆结构为例， 运用点阵结构对其进行轻量化设计。 根据连杆的工作特点， 对底部的螺栓孔做固定约束， 在顶部圆环内中心设置远程力， X 和Z 方向各100 N。

按照以上载荷边界条件分析（见图4）。

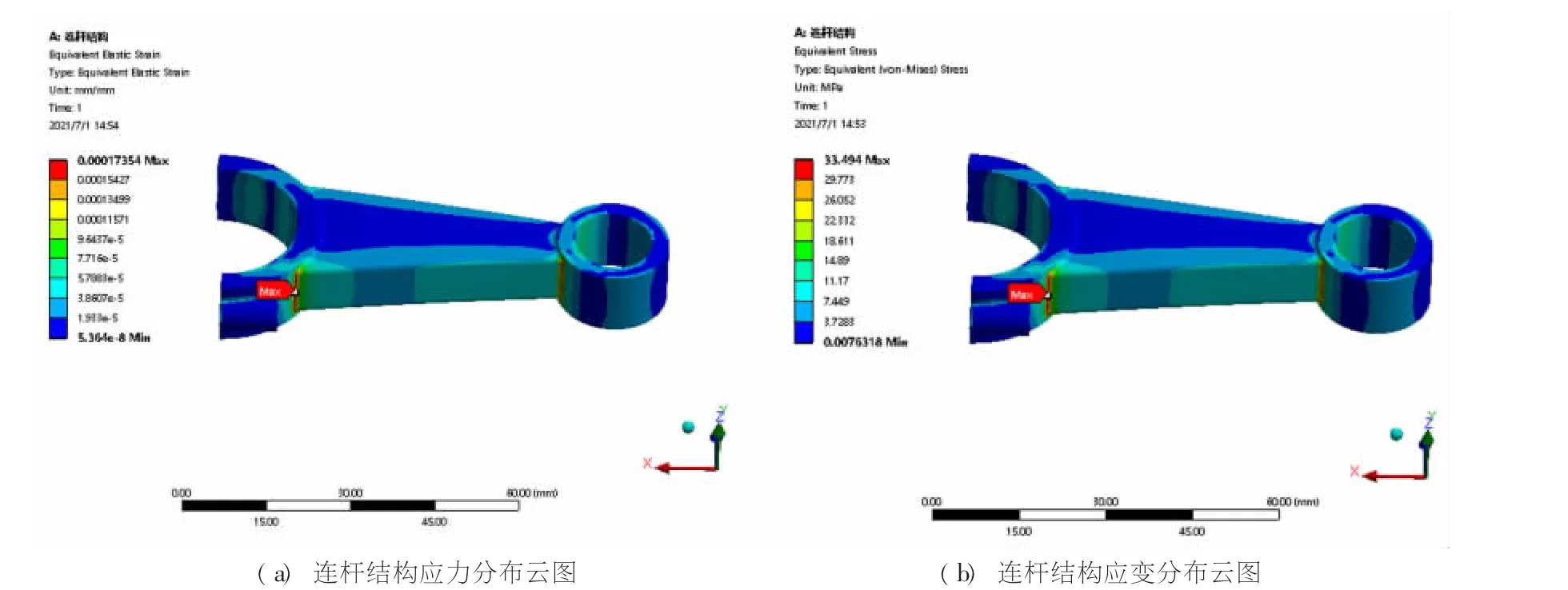
图4 连杆机构有限元分析结果

通过应力分布可以看出， 整体结构最大应力集中在连杆与底部圆环的连接侧， 由于载荷条件的特殊性， 可知整体结构最危险的地方就是连杆与顶部圆环、 底部圆环的连接部分， 此外， 连杆中间部分的应力非常小， 应力集中在外侧， 故从轻量化角度考虑， 填充部分选择在连杆中间位置以实现轻量化设计（见图5）。

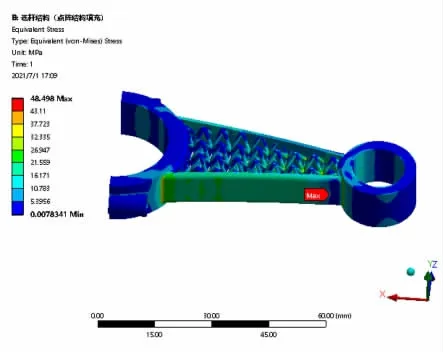
图5 连杆-点阵结构填充效果图

填充后的模型转边界条件与载荷条件保持不变， 再次分析得到填充后的结果（ 见图6～7， 表1）。

表1 连杆结构填充前后有限元分析结果

图6 连杆-点阵结构有限元分析结果

结果表明， 填充前后连杆的质量及体积均发生较大改变， 填充后重量下降41.67%， 体积下降41.34%； 连杆整体结构的应力分布发生改变， 填充前， 连杆中间部分的应力很小， 填充后整体结构的最大应力值变大， 出现在填充部位的点阵结构上。 由应力分布云图可知， 填充改变了填充部分的应力分布， 而其他部分应力分布的改变非常小。 对比发现， 点阵结构的填充不仅改善整体结构的应力分布， 且大大减轻了整体结构的重量和体积， 证明点阵结构在轻量化设计上的优势， 同样表明点阵结构对连杆结构轻量化设计的有效性。 定义相对刚度[7]为最大位移量与模型体积的比值， 通过计算得出填充后模型的比刚度是填充前的2.66 倍，故应用点阵结构同时实现轻质与提升连杆结构刚度的功能。

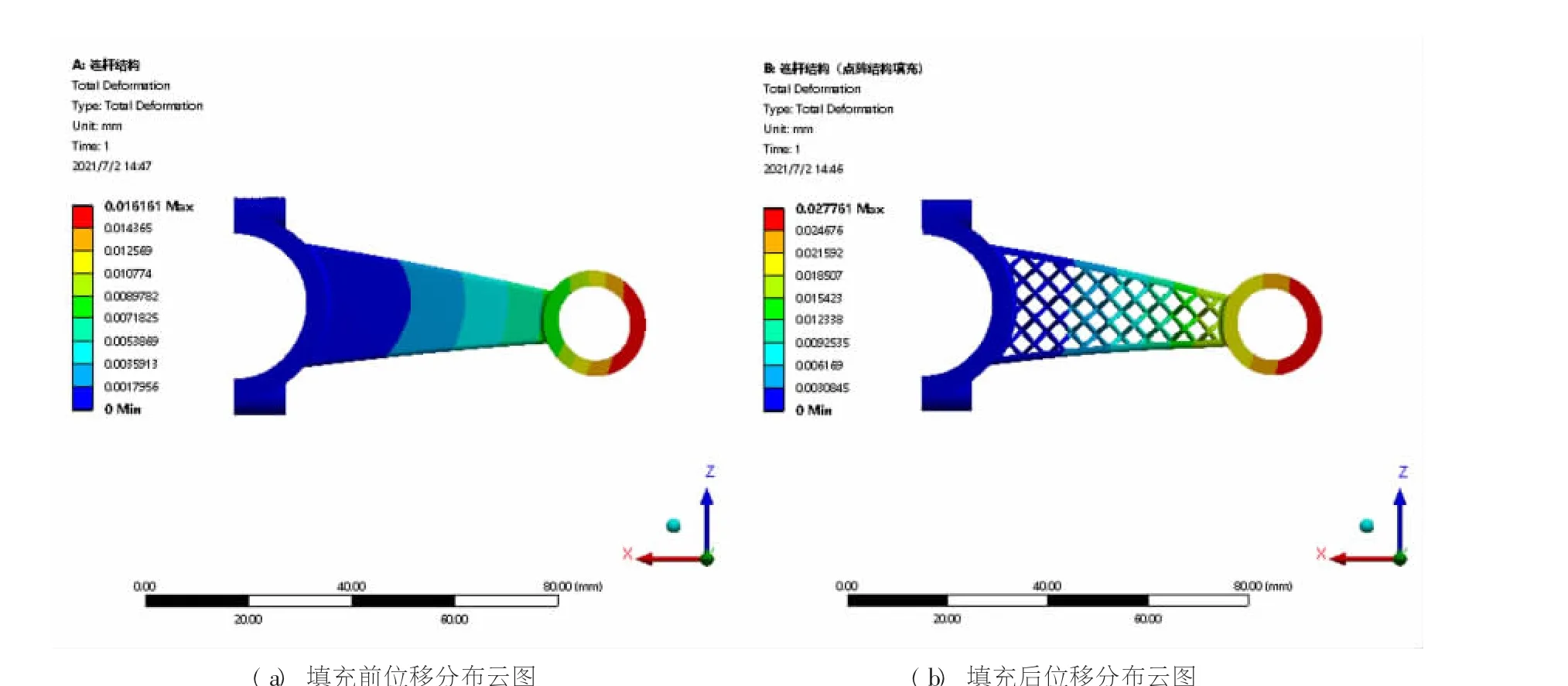
图7 连杆结构填充前后位移分布云图

4 结 语

随着增材制造技术不断发展， 点阵结构的制备更加方便， 成本大大降低， 点阵结构的应用更加广泛。 现在， 全球对点阵结构性能及应用的发掘仍在继续， 包括点阵结构快速建模软件、 点阵结构力学性能分析方法的开发， 对点阵结构特性的探索及点阵结构快速填充技术的实现等。