复合驱动式水下机器人结构及水动力系数计算
李润龙,张 禹,孙艺展
二十一世纪以来, 人类大力开发天基着陆系统、 极地考察机器人等去探索、 开辟人类新的发展空间。 作为地球生命的发源地, 海洋蕴藏着大量矿物资源与原材料供给人类社会可持续发展需要[1]。 目前全球已有大量国家发展海洋相关产业。我国拥有广阔的海洋疆域和海岸线, 拥有大量资源等待开发[2]。 为了更好地了解海洋, 获取实际经济价值, 我们必须持续研发先进的海洋技术,而水下机器人是一个重要的领域。
水下机器人凭借自身灵活机动的特性, 依靠自身电池或者脐带电缆供电, 能够在较长的一段时间内, 进行水下勘探、 水环境监测和水中作业,目前在深海科学考察、 海产品培养、 水环境监测、国防军事研究等多个领域已有较多的实际应用[3],成为各国家优先研制的先进海洋装备。 水下机器人使海洋探测与资源获取进入新阶段。 水下机器人是一种能够代替人类, 在复杂的海洋环境进行水下作业的智能装置。 当前水下机器人主要包括载人水下潜器 (HOV) 、 有缆遥控水下机器人(ROV) 和自治无人水下机器人(AUV) 等几种类型, 其中有缆遥控水下机器人又分为自航式、 拖拽式两种[4]。HOV 自身体积较大, 水下行动较为笨重。 AUV 并不使用脐带电缆进行岸基供电, 所以具有较大的活动范围, 也比较灵活, 但是由于自身携带电池有限, 不能进行长时间的水下作业。 而ROV 由上位机或者母船通过电缆供电, 能够较长时间在水下作业, 是目前应用最广的水下机器人。
本文提出一款复合驱动式水下机器人, 通过螺旋桨推进器和履带爬行机构实现水中游动与海底爬行, 通过数学建模与水动力仿真, 获得相关水动力参数, 为结构优化与运动控制提供数据基础和理论支撑。
1 结构设计
复合驱动式水下机器人由浮游部分、 主框架、爬行部分等装置组成(见图1)。
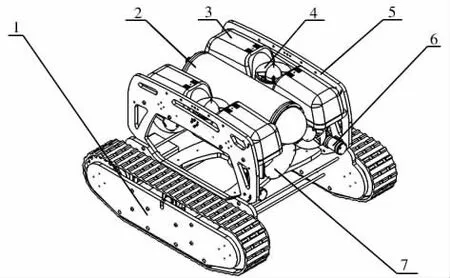
图1 水下机器人结构图
复合驱动式水下机器人采用开架式结构。 其中, 浮游装置主要由电子舱、 电池舱、 推进器、 主框架、 浮力材、 水下灯等组成, 主体框架采用HDPE 材料, 通过两个推进器垂直布置与四个推进器环形矢量布置, 以实现机器人在水下进退、 升沉、 横移、 转艏、 横滚五自由度运动[5]。
爬行装置主要由履带驱动装置及水下电机、 连接杆、 保持架等组成( 见图2) , 采用战车型履带底盘的优点是行驶稳定, 接地比压小, 拥有一定的迎接角和离去角使其具备一定的爬坡、 越障能力,适用于海底环境[6]。
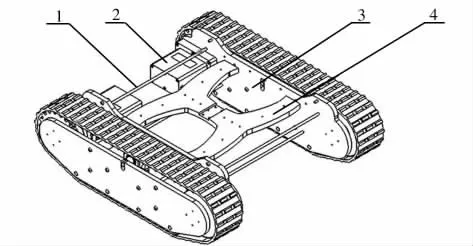
图2 爬行装置结构图
履带驱动装置由防水履带、 导向轮、 驱动轮、支重轮、 托链轮、 传动轴、 张紧装置与侧板等组成( 见图3) 。 其中, 张紧结构与托链轮设计为一体,通过调整螺栓即可进行张紧, 这一结构大大减少机器人的复杂性, 各个轮子与侧板均使用HDPE 材质, 在减轻重量的同时, 还能提供一定的浮力。

图3 履带驱动装置结构图
2 复合驱动式水下机器人运动建模
2.1 坐标系建立与参数定义
为了研究ROV 的运动, 首先需要建立描述ROV 运动的坐标系, 或称参考系。 本文根据国际水池会议 (ITTC) 推荐和造船与轮机工程学会(SNAME) 术语公报的体系, 建立固定坐标系和运动坐标系O-xyz[7](见图4)。

图4 复合驱动式水下机器人坐标系
固定坐标系是一个右手直角坐标系, 它以岸基或海洋任意选取的一点为原点, ζ 轴的正方向垂直指向地心, ζ 轴保持水平, 一般以ROV 的主航向为正向, η 轴与x 轴在水平面内相互垂直。 运动坐标系O-xyz 与固定坐标系同为直角坐标系, 固定于ROV 上, 随船体运动, 原点O 一般选在ROV 的重心G 处, 即O 与G 重合。 Ox 轴指向船艏部, 平行于水线面, Oy 轴垂直于Ox 轴, 指向ROV 右舷,并与水线面平行, Oz 轴指向ROV 正下方, 与水线面垂直(见表1)。

表1 ROV 运动参数定义
2.2 水下机器人的运动建模
(1) 平移运动方程
通过刚体动量定理可以得到水下机器人受到的外力与运动参数之间的关系, 在固定坐标系中为[8]:

一般情况下, 水下机器人运动坐标系原点O与其自身重心G 不重合。 在固定坐标系条件下我们将重心平移速度做如下表示:

式中: V—运动坐标系原点运动速度(m/s) ; Ω—运动坐标系旋转角速度(rad/s) ; RG—运动坐标系原点到重心距离(m)。
Ω×RG为牵连速度, 将式(2) 带入式(1) 可得, 水下机器人在固定坐标系中的重心加速度VG:
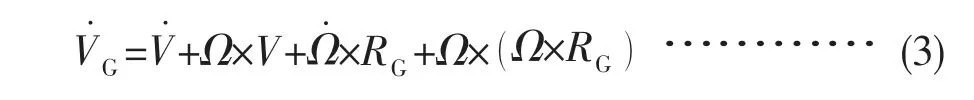
在大地坐标系中原点的加速度设为V˙, 同一坐标系中角加速度设为Ω˙, 将V、 V˙、 Ω、 Ω˙、 RG矢量与其分量带入受到的合力、 关于重心的加速的公式, 整理后可得各分力的表达式, 分别沿着运动坐标系的三个方向, 即复合驱动式水下机器人的平移运动方程:
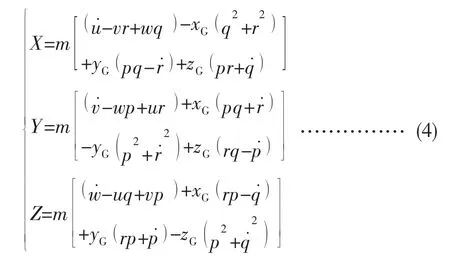
(2) 旋转运动方程
根据动量矩定理: 对于固定坐标系下的运动,刚体对原点动量矩的变化率等于该瞬时外力的合力对原点的矩:

由于复合驱动式水下机器人整体结构关于x-z平面完全对称, y-z 平面近似对称, 所以Ixz=Izx=Ivz=Izv=0。 再将V、 V˙、 Ω、 Ω˙、 RG矢量分量带入上式, 可得水下机器人的旋转运动方程:

由平移运动方程和旋转运动方程共同组成了水下机器人六自由度空间运动方程。
3 基于FLUENT 流体仿真建模
建立CFD 仿真模型, 是数值模拟计算的首要步骤, 机器人长和宽约为600 mm, 高约为365 mm, 在CFD 仿真计算中, 过于复杂的仿真模型结构会使网格划分十分困难, 降低数值计算的求解精度, 所以笔者对模型进行简化处理(见图5)。

图5 简化模型
为了保证模型周围流场能够充分发展, 提高计算结果的准确性, 将控制域长度设置为10 L( L为机器人横向长度) , 流域入口与机器人艏部距离为3 L, 艉部距离流场出口为6 L, 控制域宽度与高度取机器人长度的7 倍, 即7 L[9], 笔者对控制域进行划分(见图6)。
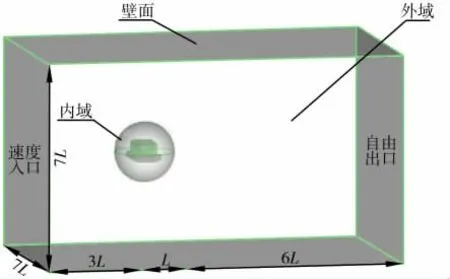
图6 控制域示意图
ROV 模型采用混合网格划分形式, 将控制域划分成内域、 外域两部分[10]。 其中, 内域为包括ROV 整体在内的球形域, 采用四面体非结构化网格划分形式, ROV 本体表面采用三角形非结构化网格划分形式( 见图7) 。 外域由其他剩余的外流场组成, 采用非结构四面体网格和棱柱体网格进行划分, 通过多次实验计算, 最终选取网格数量为150 万。

图7 ROV 表面网格
4 水动力仿真实验
本文基于FLUENT 模拟机器人直航、 斜航及加速直航运动实验, 获取复合驱动式水下机器人相应的水动力系数。
4.1 水平直航
由于ROV 结构左右完全对称, 前后近似对称[11], 上下不对称, 所以仅取y 轴正方向, x 轴和z 轴的正、 负两方向进行直航实验。 以x 方向直航为例, 设定入口流速0.2~1.6 m/s, 得到ROV 以0.8 m/s 在水中沿x 正方向直航运动时的压强云图与速度云图(见图8~9)。
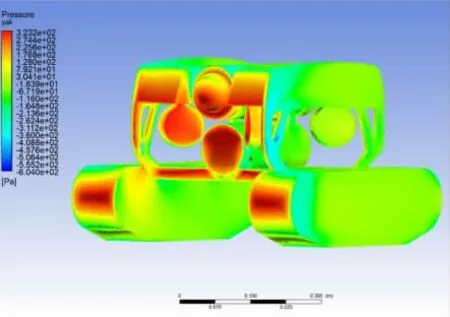
图8 压力云图

图9 XZ 面速度云图
笔者将得到的数据在MATLAB 中拟合, 可以看到, 随着纵向速度增大, ROV 前进与后退的阻力值呈线性增长, 同时, 由于ROV 前后近似对称,模拟纵向运动时, 前进与后退阻力值相差不大(见图10)。
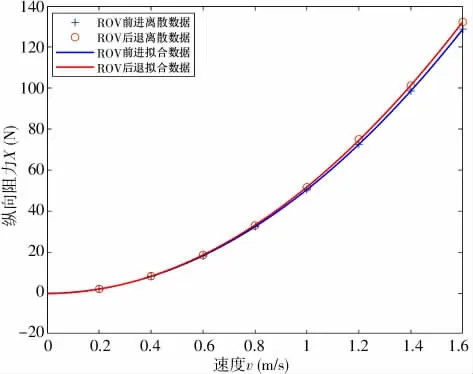
图10 水平面x 方向直航阻力拟合曲线
拟合后得到方程为:
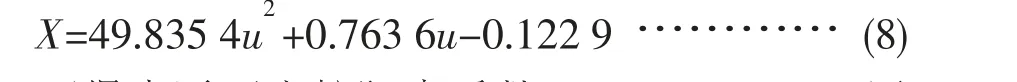
可得水平面直航阻力系数Xuu=-49.835 4, 通过无因次化处理后可得到X′uu=-0.277 4。 通过相同方式的仿真处理, 可以得到沿y、 z 方向直航运动的阻力拟合曲线(见图11~12)。
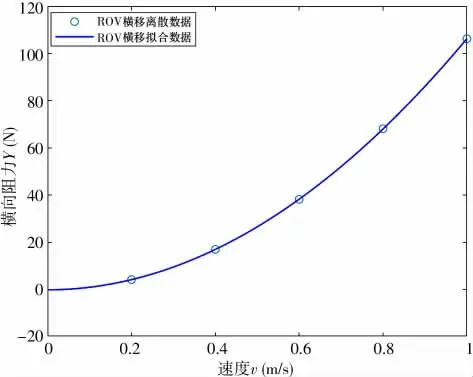
图11 水平面y 方向直航阻力拟合曲线
拟合后得到水平面直航阻力系数Yvv=-105.9,通过无因次化处理后可得到Y′vv=-0.589 4。


得到水平面直航阻力系数Zww=-105.9, 通过无因次化处理后可得Z′ww=-0.589 3。

图12 水平面z 方向直航阻力拟合曲线
4.2 水平斜航
将直航时沿x 轴拖曳的已画好的网格, 通过网格旋转技术, 将网格外域相对于内域, 整体绕z 轴旋转漂角, 分别以0.5 m/s 和1.0 m/s 模拟水平斜航运动。 以ROV 速度U=1.0 m/s 为例, 得到漂角β分别为2°、 4°、 6°、 8°时的速度云图(见图13)。

图13 水平斜航速度云图
笔者将两种速度仿真数据进行拟合, 得到ROV 所受横向力Y、 艏摇力矩N 与横向速度的关系曲线(见图14~15)。
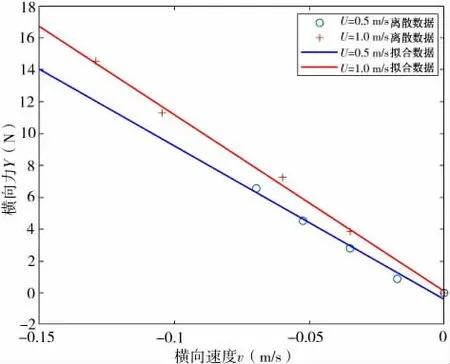
图14 水平斜航阻力拟合曲线
通过拟合, 可得到系数Yv、 Nv, 将其进行无因次化处理后, 可得到水动力系数Y′v=-0.575 9、N′v=-0.331 8。

图15 水平斜航阻力矩拟合曲线
4.3 垂直斜航
笔者将直航时沿x 轴拖曳的网格外域进行旋转, 转动冲角分别取±2°、 ±4°、 ±6°及±8°, 将内、外域相互拼接, 得到垂直斜航所用网格。 分别设置入口流速0.5 m/s 和1 m/s, 模拟水平斜航运动。笔者给出1 m/s 的速度云图(见图16)。
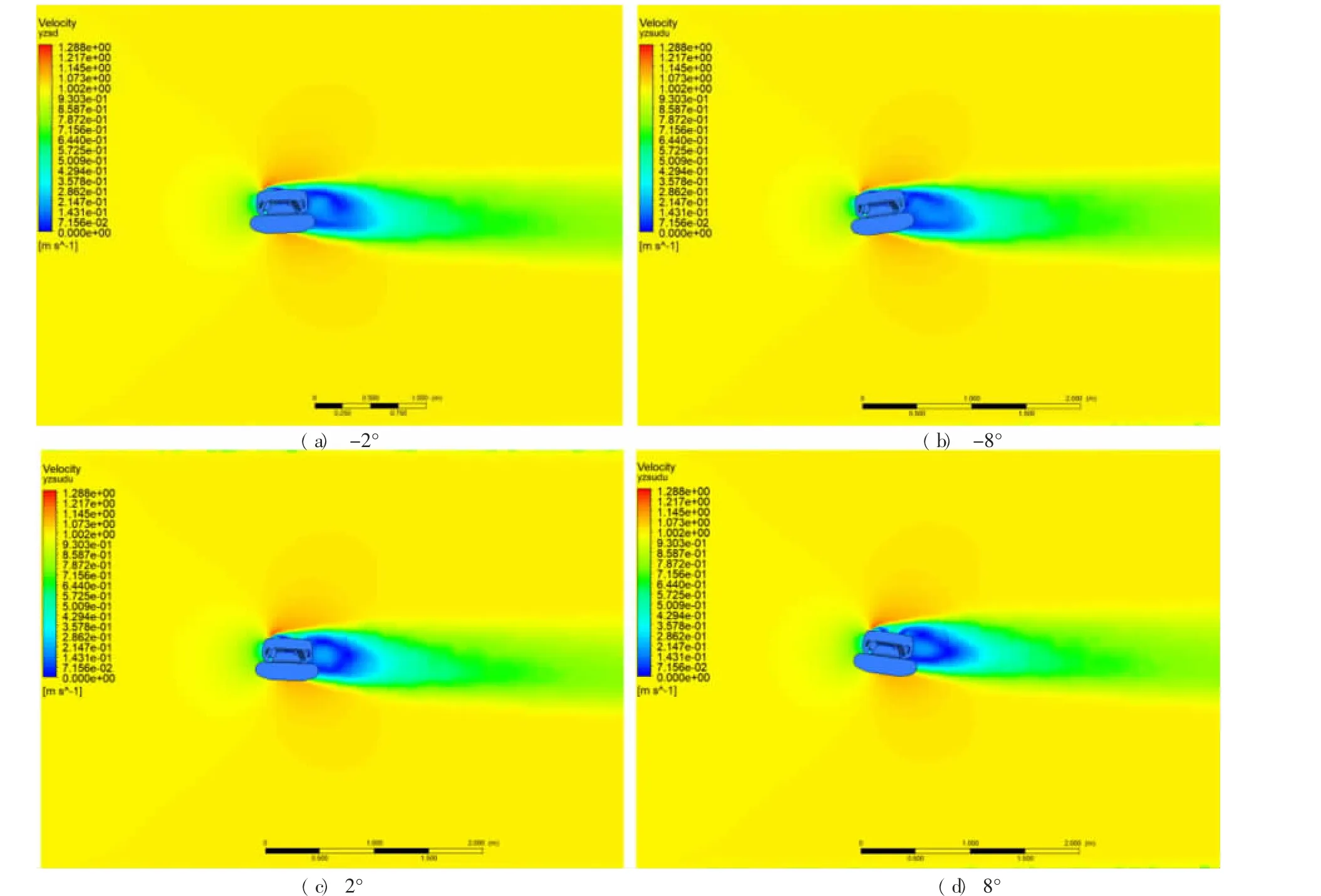
图16 垂直斜航速度云图
将数据进行拟合, 得到ROV 所受横向力Y、俯仰力矩M 与横向速度的关系曲线( 见图17~18)。
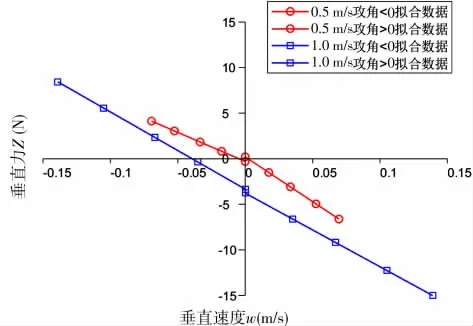
图17 垂直面斜航阻力拟合曲线
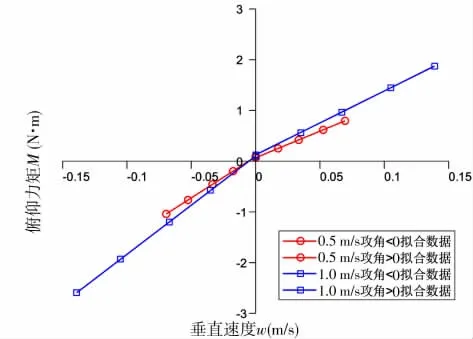
图18 垂直面斜航阻力拟合曲线

4.4 加速直航
ROV 沿x 轴方向做匀加速运动[13]、[14], 模拟中,先计算ROV 以速度1 m/s 直线运动时的纵向阻力为F=-50.528 N, 然后将编写好的UDF 导入到FLUENT 中模拟a=1 m/s2的匀加速运动, 仿真计算时, 初速度V=0.8 m/s, 设置单位时间步长0.001,步数为200, 最大迭代次数为20 步(见图19)。
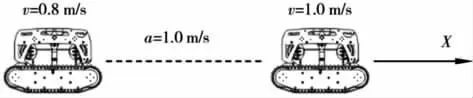
图19 加速直航原理图
根据以上编写UDF(见图20)[15]。

图20 加速直航UDF
计算后得到当速度达到1 m/s 时, 纵向阻力Fa=-65.476 N。 根据牛顿第二定律可得到附加质量为:

5 结 语
本文根据水下作业与海地检测要求, 设计一种复合驱动式水下机器人, 具备水中游动与海底爬行能力。 针对复合驱动式水下机器人的特点, 建立运动方程, 完成模型简化, 对控制域整体进行网格划分, 模拟机器人直航、 斜航及加速直航运动实验,得到相应的水动力系数, 作为模型结构优化及运动控制的数据基础和理论支撑。

