基于永磁弹簧的变刚度关节驱动器设计

都智勇，赵文博，孙龙飞

变刚度机构是仿生关节的关键组成部分， 是区别于传统刚性驱动器的重要部件， 能够直接影响关节的变刚度性能[1]。 它们的区别在于变刚度机构在驱动构件和执行构件间可以串联或并联刚度可调的弹性元件[2]， 通过改变弹性元件受力的大小来实现关节刚度的非线性变化[3]； 根据变刚度柔性关节的特性， 可以实现在非结构环境下人机交互的安全性[4]。 本文依据永磁弹簧在工作时呈现非线性的特点对机器人关节内部变刚度机构进行研究， 设计出一种基于永磁弹簧的变刚度驱动器结构， 使绳索与永磁弹簧相连， 利用蜗轮、蜗杆转动使绳索的长度变化， 改变永磁弹簧的气隙间距， 实现机器人关节刚度的变化。

1 变刚度原理分析

本文的永磁变刚度关节驱动器基于绳索驱动永磁弹簧单元进行构建。 永磁弹簧为一对永磁体同极相对布置， 在永磁体间气隙间距变化的同时， 永磁弹簧的斥力也发生改变（ 见图1） 。 气隙间距越小， 永磁体间斥力越大， 永磁弹簧的等效刚度越大。

图1 永磁弹簧结构示意图

变刚度装置采用柔性绳索经定滑轮牵引动滑轮及移动永磁体沿移动约束方向滑动， 改变永磁弹簧气隙间距， 即固定永磁体与移动永磁体间距。 通过改变绳索长度调整永磁弹簧气隙间距， 改变永磁弹簧的等效刚度。 驱动器内圈在外部扭矩T 的作用下， 永磁弹簧气隙间距改变量为Δx， 关节内圈和外圈产生相对转角θ。 不同气隙间距下的外部力矩T 所产生的角度θ 不同， 关节的等效扭转刚度也不同， 由此实现变刚度控制（见图2）。

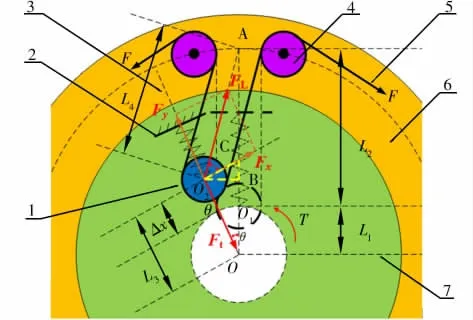
图2 变刚度原理示意图

2 变刚度驱动器结构设计

基于上述绳索-永磁弹簧变刚度的工作原理，笔者设计永磁变刚度关节驱动器（ 见图3） 。 变刚度关节驱动器的内圈与外圈可以相对转动， 永磁弹簧通过支架和直线导轨安装于内圈， 其中， 固定永磁体与支架固连， 移动永磁体安装于滑块， 固定永磁体与移动永磁体发生相对运动形成永磁弹簧（见图3（ a）） 。 绳索绕过外圈定滑轮及滑块动滑轮，通过改变绳索长度调节移动永磁体与固定永磁体间的气隙间距， 改变永磁弹簧初始刚度。 蜗杆驱动蜗轮及与蜗轮连接的绕线轮实现收放线动作， 驱动器输出轴与内圈固定连接， 同步转动（见图3（b））。

图3 变刚度驱动器结构示意图

3 绕线蜗轮蜗杆尺寸计算

笔者计算蜗杆传动的几何尺寸（ 见图4） ， 当每组永磁弹簧产生70 N 的弹力时， 关节中三组永磁弹簧共产生210 N 弹力， 设滑轮半径为15 mm，则蜗杆的输入功率

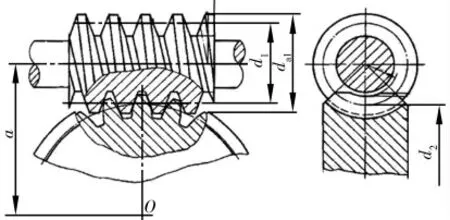
图4 蜗杆传动的几何尺寸

当蜗杆转矩为T1=210×15=3 150 N·mm=3.15 N·m， 蜗杆的转速n1=30 r/min 时， 蜗杆的输入功率P1为9.86 W。

（1） 确定作用在蜗轮上的转矩

因为蜗轮、 蜗杆自锁， 所以蜗杆头数z1=1， 在蜗杆传动设计中， 传动比的公称值按下列数值选取： 5、 7.5、 10、 12.5、 15、 20、 25、 30、 40、 50、60、 70、 80。 本文取z2、 i 的推荐值（见表1）。

表1 z1、z2、i的推荐值

蜗轮的齿数z2一般取27～80。 z2过少将产生根切； z2过大， 蜗轮直径增大， 与之相应的蜗杆长度增加， 刚度减小。

式中： KA—使用系数； KV—动载系数； Kβ—齿向载荷分布系数。

因绕线轮工作载荷稳定， 所以选取Kβ=1， 选取KA=1（ 见表2） ， 蜗轮圆周速度小于3 m/s 时取1.0～1.1， 取KV=1.05， 所以此时确定载荷系数K=1.05。

表2 使用系数KA推荐值

（3） 确定ZE， ZP及[σH]

根据蜗轮材料为铸锡磷青铜ZCuSn10P1， 采取金属模铸造， 蜗杆硬度＞45 HRc， 得出铸锡青铜蜗轮的基本许用应力[σH]′=268 MPa（见表3）。

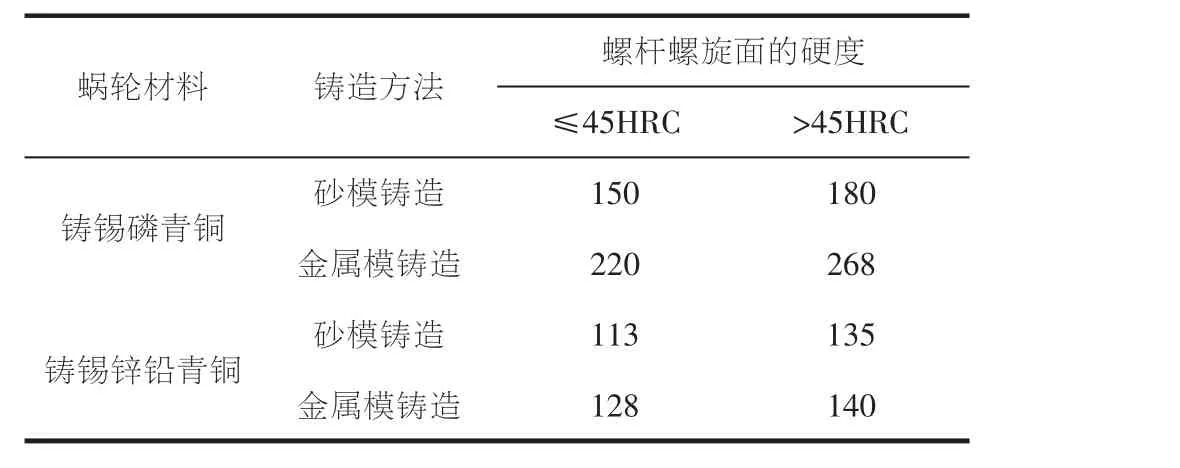
表3 基本许用应力推荐值选取

应力循环次数为速（min-1）； Lh—工作寿命（h）。

式中： j—每转每个轮齿啮合次数； n2—蜗轮的转

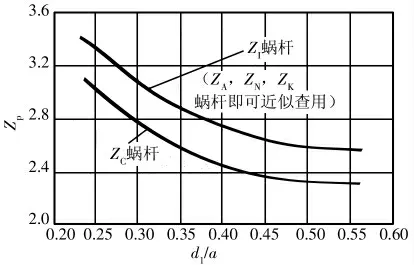
图5 ZP的选取

（5） 主要几何参数

蜗杆直径系数取q=12.5， 蜗轮齿数z2=i×z1=50；计算得出蜗杆的分度圆直径d1=Ø20 mm， 蜗轮分度圆直径d2=Ø80 mm； 蜗杆齿顶圆直径da1=Ø23.2 mm， 蜗轮齿顶圆直径da2=Ø83.2 mm； 蜗杆齿根圆直径df1=Ø16.16 mm， 蜗轮齿根圆直径df2=Ø76.16 mm（见表5）。

表5 蜗轮蜗杆几何尺寸计算

4 结 语

（1） 本文提出一种基于永磁弹簧的变刚度机器人关节驱动器， 运用同极永磁体随气隙间距变化产生的非线性斥力进行关节刚度调节。

（2） 该关节的初始刚度通过电机驱动蜗杆蜗轮产生转动改变绳长， 进而改变永磁弹簧气隙间距得到。 由于蜗轮、 蜗杆可以自锁， 故电机无需始终处于伺服状态， 降低能耗。

表4 蜗杆基本尺寸及其与蜗轮参数的匹配

（3） 通过本文计算得到绕线驱动蜗轮、 蜗杆的结构参数。