关于七上《3.5去括号》一课教学的思考

刘惠

摘要：初中引入正负符号以及代数式概念后，使得去括号、定符号变成计算的难点。实际上学生只要能熟练地掌握“同号得正，异号得负”这一定符号原则，去括号也能变成小菜一碟。因为任何去括号问题都可根据乘法分配律简化为定符号问题和简单的数字乘法问题。

关键词：去括号;乘法分配律;同号得正;异号得负

一、发现问题

教材中总结出去括号法则：括号前面是“+”号，把括号和它前面的“+”号去掉，括号里各项的符号都不改变;括号前面是“-”号，把括号和它前面的“-”号去掉，括号里各项的符号都改变.然而很多学生在运用法则去括号时容易犯错，学生对于哪些项的符号该变还是不该变特别容易混淆，尤其像“-（2m-3）=”，容易错写成“2m+3”，其实是学生并没有理解括号外的“-”是针对括号内各项而言的，或者学生并没有搞清括号内第一项原本是什么符号，以为原本是“-”号，然后根据法则要变号，就变成了正号。为了帮助学生规避这种混乱错误，笔者通过对去括号本质的思考，对这节课的教学进行了部分创新设计，并在实际教学中实施并观察，此教学创举确有成效。

二、教学设计前部分创新

（一）复习回顾

说出下列各数的意义，并化简：①-（+5） ②+（-3） ③+（+2） ④-（-6）

设计意图：多重符号化简的本质是求一个数的自身或其相反数，进而归纳“同号得正，异号得负”，便于学生理解今后去括号时为什么括号里各项的符号都不改变（自身）或者都改变（其相反数）。

（二）新课引入

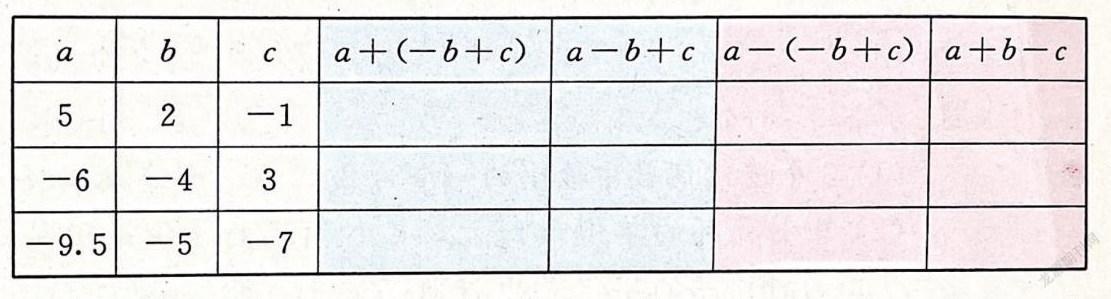
填表：

学生猜想发现：a+（-b+c）=a-b+c;a-（-b+c）=a+b-c

学生归纳法则：括号前面是“+”号，把括号和它前面的“+”号去掉，括号里各项的符号都不改变;

括号前面是“-”号，把括号和它前面的“-”号去掉，括号里各项的符号都改变.

提问1：你是如何理解符号不改变和符号要改变的？

慢慢引导学生回答：“+”号对括号内各项没有影响，因此符号不改变，“-”号是求相反数，括号前的“-”号是作用于括号整体，因此要对括号内各项求相反数。（即a-（-b+c）=a-（-b）-（+c）再对每一项进行多重符号化简）

提问2：3（x+y）=——？-2（x-1）=——？依据是什么？

学生答：3（x+y）=3x+3y，-2（x-1）=-2x+2，依据的是乘法分配律。

设计意图：括号前是数字3或者数字-2，要与括号整体相乘，用乘法分配律将数字与括号内各项都相乘，需先定符号再数字相乘。类比数字与括号整体乘法，学生易理解去括号法则的依据就是乘法分配律，再根据“同号得正，异号得负”定符号，即a-（-b+c）=a-（-b）-（+c）

=a+b-c（其实a-（-b+c）=a-（-b）-（+c）这个又可以归为写成省略括号的和的形式，根据“同号得正，异号得负”定符号，关键还是要理解括号前的“-”号是作用于括号整体的）。

（三）总结归纳

去括号方法1：去括号法则

去括号方法2：依据乘法分配律，重点在于根据“同号得正，异号得负”定符号。

說明：也可跟学生解+（-b+c）可看成+1·（-b+c）;-（-b+c）可看成-1·（-b+c），因此本质就是乘法分配律。这样所有去括号都可运用乘法分配律。当然，去括号两种方法都可以，看学生的接受，让学生自主选择哪种方法更容易。

（四）练习

a+（b-c）=  ;4（-b+c）=  ;-2（m-2）=  ;a-（b+c）=  ;a-（-b+c-d）=  .

提问：你是如何去括号的？哪种方法适合你？

三、创新教学的情况反馈

去括号两种方法已讲授，方法1需先判断括号前的符号，并重点判断括号内第一项的符号，再思考变还是不变。方法2需注意括号外的符号（连同符号的数）与括号内各项都要乘并定符号。让学生用自己的理解运用方法练习去括号，学生自然能选择出适合自己的方法，当然笔者去括号时自然而然地运用的是乘法分配律，眼观括号内外符号，条件反射根据“同号得正，异号得负”定符号。根据实际教学的反馈情况，确实大部分同学认为运用方法2不易错。总之学生只需记住遇到去括号问题一律用乘法分配律与括号内各项相乘并定符号。

四、结语

符号问题和括号问题一直是学生的痛点，也是计算容易出错的地方。当遇到多重符号化简那就有去括号，或者遇到去括号那就有多重符号化简，因此去括号虽然本质是依据乘法分配律，但最终还是要根据“同号得正，异号得负”这一口诀进行化简。而且这一口诀始终贯穿于初中三年的计算问题，因此学生不仅要掌握去括号方法，还要知道其本质。养成对任何知识方法都要“知其然，也要知其所以然”的学习习惯，而不是死记硬背，不明所以。

参考文献：

[1]穆康.浅谈初中数学“去括号法则”的教学与思考[J].学苑教育，2011（01）.

[2]许俊波.初中数学“去括号法则”的教学分析[J].数理化解题研究，2017（11）：22.

[3]邹意.“去括号”教学创新实践[J].中小学数学（初中版），2020（Z2）：106-108.