混有网联车队的道路通行能力分析

秦严严，唐鸿辉，杨金滢，李淑庆

(重庆交通大学 a.交通运输学院，b.重庆市交通运输工程重点实验室，重庆 400074)

近年来，交通系统信息化和智能化技术取得了快速发展，这使得未来交通系统全面实现智能化成为可能.网联车辆可利用车车通信(Vehicle to Vehicle, V2V)及车路通信(Vehicle to Instruction, V2I)技术实现车辆运动信息实时共享，进而形成柔性车队，一定规模的车队组织模式有望实现道路通行能力的极大提升[1-3].

国内外学者对车队组织方面进行了相关研究，部分学者通过研究网联车辆组队，认为队长是提高通行能力的主要因素[4-7].如Chen等[8]通过建立混合交通流通行能力计算公式，研究网联车辆渗透率和车队规模对道路通行能力的影响.Bujanovic等[9]研究了不同车队规模限制下通行能力之间的差异，认为车队规模的大小对于车队机动性十分重要.Zhou等[10]通过建立描述通行能力的解析表达式，仿真验证了较大的车队规模有助于通行能力的提高.而其他学者对车队的研究则大都集中于车队组织控制策略方面[11-13]，部分文献针对人工车辆和自动驾驶车辆混行交通流进行了仿真研究.如秦严严等[14]针对混有人工车辆、自适应巡航控制(Adaptive Cruise Control,ACC)车辆和协同自适应巡航控制(Cooperative Adaptive Cruise Control, CACC)车辆的异质交通流通行能力进行了数值仿真试验，其结果表明异质交通流基本图解析能代替基本路段通行能力仿真实验，进一步地，以混合车流基本图模型为基础，提出了混合交通流(Lighthill-Whitham-Richards，LWR)模型，并论证了所提LWR模型能定量化分析交通拥堵演化的传播机制[15].徐桃让等[16]分析了智能网联车辆与人工驾驶车辆反应时间差异与智能网联车辆比例对异质交通流通行能力的影响，但较少考虑车队组织模式对宏观交通流的建模分析.常鑫等[17]对网联车辆渗透率和车队规模等参数进行敏感性分析，认为网联车辆渗透率提高和车队规模增加有利于提升通行能力.

通过以上分析可以发现，国内外学者对混有网联车队的混行交通流研究涉及多个方面，但较少考虑到混有多种网联车队对混行交通流的影响，研究多种网联车队混行，分析其影响通行能力的最佳车队规模，对研究混合交通流通行能力具有重要意义.基于此，本文作者考虑了两种网联车队的混行交通流，在该混行交通流中，提出分布比例与基本图模型，并分析两种网联车队规模以及两种网联车辆渗透率对通行能力的影响.

1 网联车队混行交通流及数学解析

1.1 跟驰模式分析

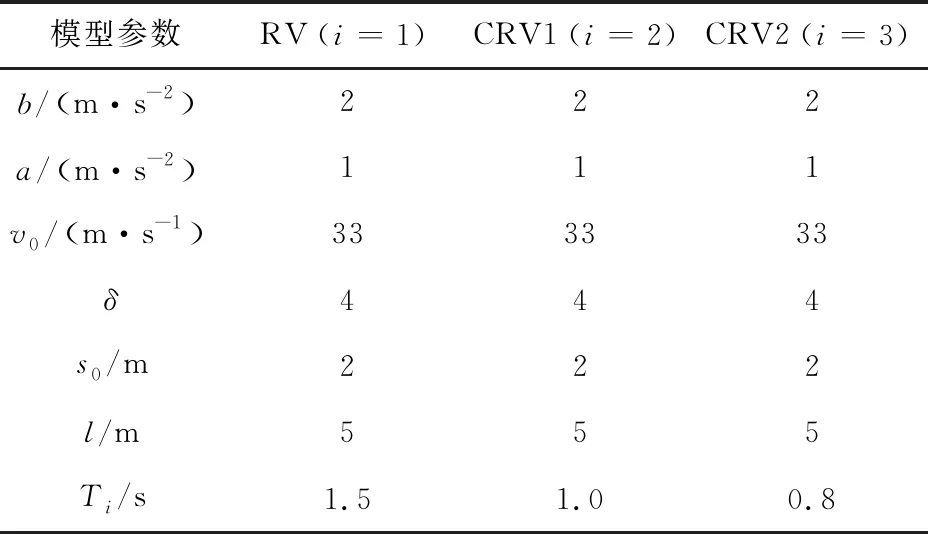
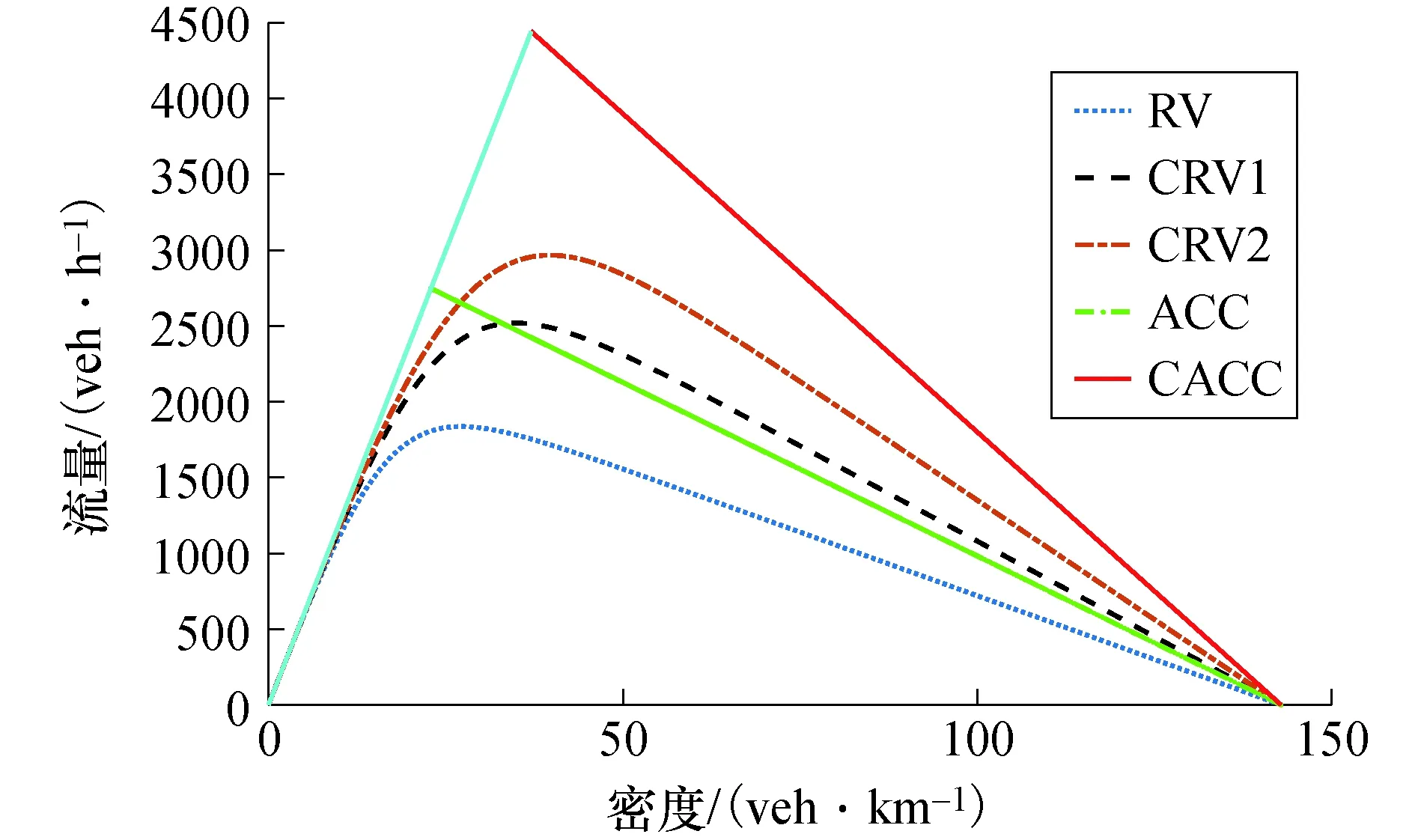
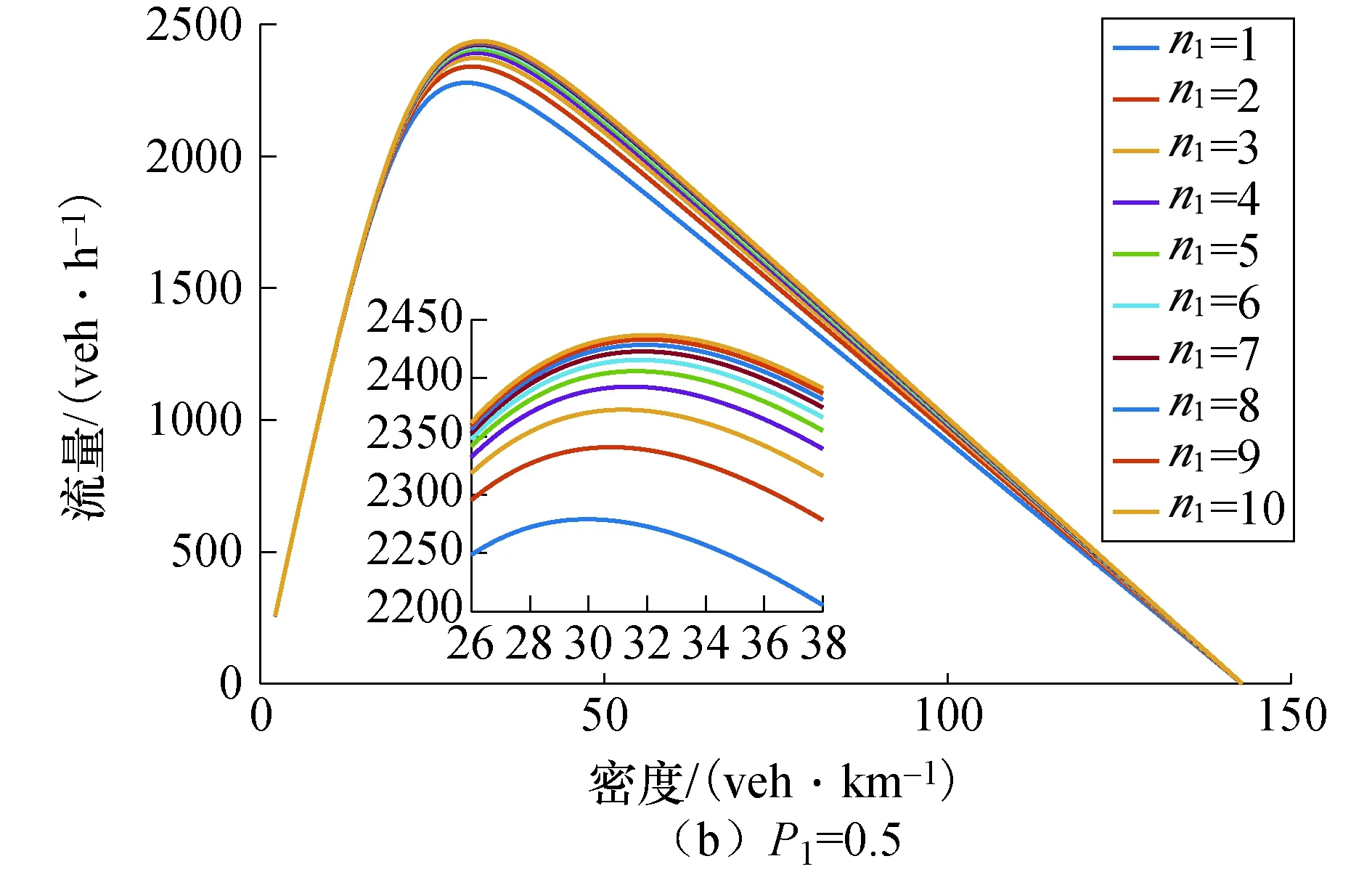
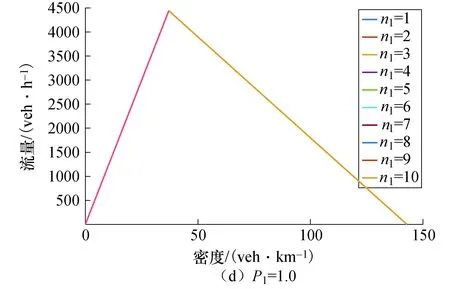
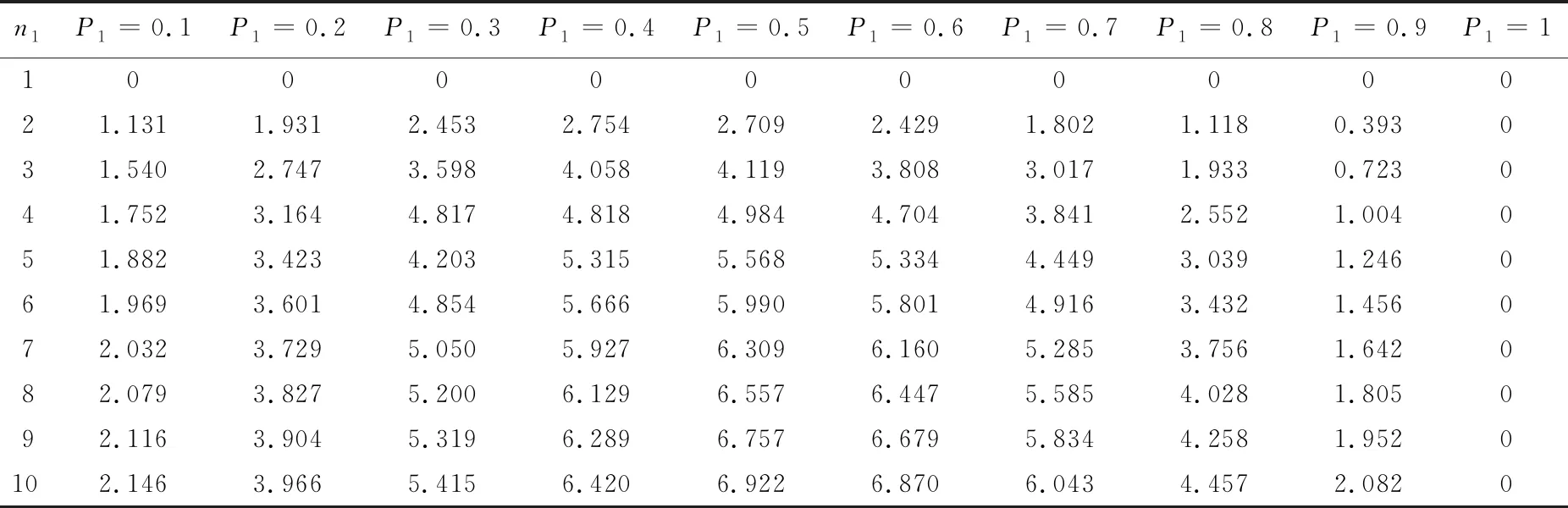
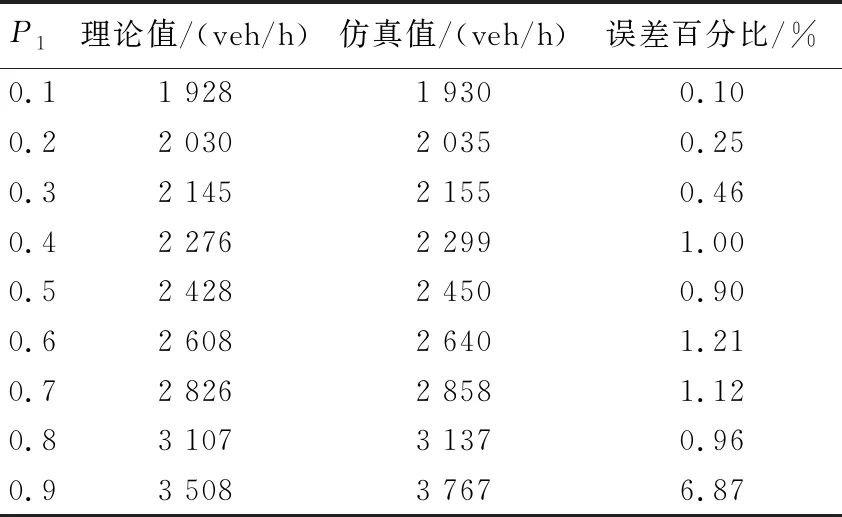
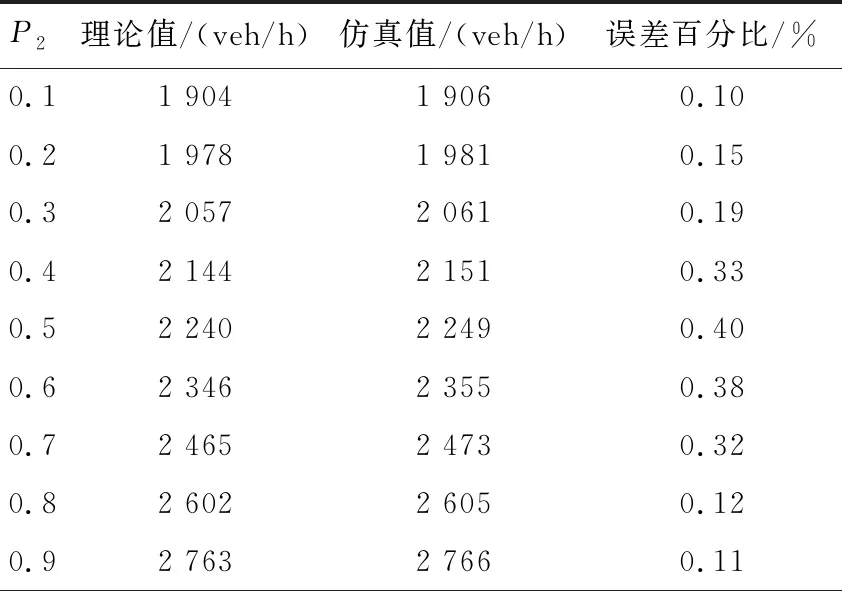
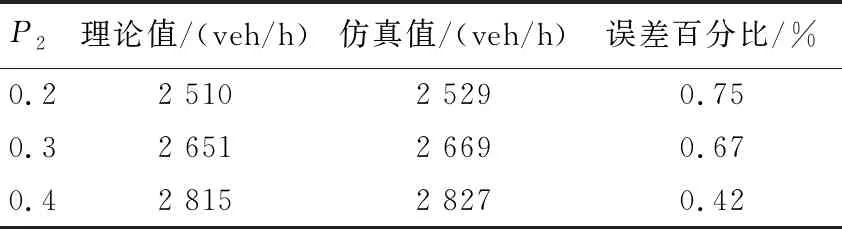
基于车联网技术，空间连续的网联车辆能组成柔性车队，队内车能维持更小的车头间距跟驰前车[17]，在混行交通流中，同类型的网联车辆组成队列，即分别组成网联自动驾驶车队和网联辅助驾驶车队，并设定网联车队最大规模为nmax，当前方车队规模达到nmax时，后随网联车辆将重新组队并成为头车，如图1所示.在图1中，存在三种类型车辆，定义为传统人工车驾驶车辆RV、网联自动驾驶车辆CACC、网联辅助驾驶车辆CRV.CRV为装载了网联设备的人工车辆，它可利用V2V通信技术实现与网联车辆信息共享，起到辅助人工驾驶的作用.通过组合分析可知在混行交通流车队中存在9种跟驰模式，如表1所示.其中，当CACC车队跟驰前车为RV车辆时，由于RV车辆未装载网联设备，无法传递车辆运动信息，此时后方紧随CACC车队头车退化为ACC车辆，队内仍为CACC车辆，而ACC车辆的车头时距大于CACC车辆的车头时距.当CRV车队跟驰前车为RV车辆时，CRV车辆能够依靠网联设备，获取车辆运动信息，辅助驾驶员能及时地做出相应措施，而RV车辆不具备此功能，驾驶员做出反应的时间大于CRV.故后方紧随CRV车队头车(CRV1)的车头时距应大于队内CRV车辆(CRV2)的车头时距但仍然要小于RV车辆的车头时距[16-17]，而当CRV(CACC)车队跟驰CRV车队或CACC车队时，CRV(CACC)车队头车能共享前车车辆运动信息，故它的车头时距同队内车辆相同.混行交通流中平衡态车头间距存在如下关系：hCA

图1 混行交通流网联车队中的跟驰模式Fig.1 Car-following modes of connected vehicle platoon in mixed traffic flow

表1 跟驰模式及比例结构

1.2 数学解析

假设道路上CACC车辆渗透率为P1，CRV车辆的渗透率为P2，P=P1+P2，则RV车辆的比例为1-P1-P2=1-P.设道路总共有N辆车，则有N(1-P)辆RV车辆，NP1辆CACC车辆，NP2辆CRV车辆，则有NP1/n1个CACC车队，NP2/n2个CRV车队，则CACC车队、CRV车队、RV车辆比例分别为

(1)

(2)

(3)

同时，结合图1计算得到ACC、CRV1、CRV2车辆的比例分别为

PACC=PrPCACC=

(4)

PCRV1=

(5)

(6)

2 跟驰模型

2.1 智能驾驶员模型

由1.1节可知，当CRV车队跟驰前车为RV车辆时，由于RV车辆无网联设备，因此无法传递和接受前方车辆的运动信息，而CRV车辆能够实时获取自身及前方车辆的运动信息，为描述他们之间的差异，往往采用具有不同安全车头时距参数的智能驾驶员模型(Intelligent Driver Model, IDM)来反映他们之间的跟驰行为[18].

选择IDM模型作为人工驾驶车辆的跟驰模型，IDM的模型公式为[19]

(7)

依据相关文献[9,13,20]，IDM模型参数的取值如表2所示.

表2 IDM模型参数取值

2.2 PATH实验室模型

近年来，自动驾驶系统取得了快速发展，如特斯拉Autopilot、华为移动数据(Mobile Data Center, MDC)智能驾驶计算平台、以及百度Apollo等，这些自动驾驶系统的底层跟驰模型都能很好描述自动驾驶车辆的特性，但目前只有加州大学PATH实验室的模型是公开的，同时PATH实验室的模型参数标定是通过实车测试得到的数据，能够反映未来CACC车辆跟驰行为，得到了学者的普遍认可.PATH实验室的CACC跟驰模型[21]公式为

(8)

同时PATH实验室应用实车测试数据，标定了基于恒定期望车间时距的ACC跟驰模型，可较好地描述当前ACC车辆的跟驰特性[21].ACC跟驰模型公式为

(9)

式中：ka、kb为控制系数，其值分别为0.23s-2、0.07s-1；ta为ACC期望保持的恒定车间时距，其取值为1.1 s.

3 混有网联车队的交通流基本图模型

3.1 同质交通流基本图模型

针对人工驾驶车辆而言，在交通流平衡态下，令式(7)中加速度和速度差为0，计算可得人工驾驶车辆的平衡态车头间距hi为

(10)

根据交通流密度定义，可计算得到同质交通流中不同类型人工驾驶车辆的同质交通流密度为

(11)

则人工驾驶车辆同质交通流基本图模型为

(12)

式中：k为密度；q为流量.

同理，可分别得CACC、ACC车辆同质交通流基本模型为

(13)

(14)

平衡态速度的取值范围为0～33.3 m/s(自由流速度)，通过式(12)～式(14)分别得到RV、CRV、CRV2、ACC、CACC车辆同质交通流流量-密度基本图解析曲线，如图2所示.

图2 同质交通流流量-密度基本图解析曲线Fig.2 Analytical curves of flow-density basic diagram in homogeneous traffic flow

分析图2可知，当各类车型的同质交通流平衡态密度达到各自临界密度时，他们的通行能力最大，如RV车辆平衡态密度为26.79 veh/km时，最大通行能力为1 832 veh/h；CRV1车辆平衡态密度为34.90 veh/km时，最大通行能力为2 513 veh/h；CRV2车辆平衡密度为39.12 veh/km时，最大通行能力为2 958 veh/h；ACC车辆平衡态密度为22.92 veh/km时，最大通行能力为2 750 veh/h；CACC车辆平衡态密度为37.06 veh/km时，最大通行能力为4 443 veh/h.

3.2 混行交通流基本图模型

(15)

根据交通流密度定义，可以得到混行交通流的密度k为

(16)

则混行交通流的流量-密度基本图模型为

(17)

分析式(17)可知，混行交通流基本图模型与CACC车辆渗透率P1、CRV车辆P2以及CACC车队规模n1和CRV车队规模n2有关.因此，通行能力由两种类型的网联车辆渗透率及两种类型网联车队规模共同确定.

4 通行能力分析

对网联车队规模进行参数敏感性分析时，分别考虑以下三种情景，情景一：混行交通流只涉及两类车辆，即CACC车辆和RV车辆；情景二：混行交通流只涉及两类车辆，即CRV车辆和RV车辆；情景三：混行交通流同时包含三类车辆，即CACC车辆、CRV车辆及RV车辆.

4.1 网联自动驾驶车队规模对通行能力的影响

针对情景一，根据式(17)，令P2取值为0时，分析CACC车辆在不同渗透率下，CACC车队规模对混行交通流通行能力的影响.计算得到取不同渗透率P1时，不同CACC车队规模下的混行交通流流量-密度基本图曲线，如图3所示；以及不同P1、n1值下交通流最大流量变化情况，如表3所示.分析图3、表3数据知，在情景一中，当P1≤0.3，n1>7辆时，最大流量增加率变化量低于0.2%；当P1>0.3，n1>9辆时，最大流量增加率变化量低于0.2%，故当n1取值为7～9辆时，通行能力提升效果最为显著，且P1值为1时，通行能力不受CACC车队规模的影响.

图3 n1值敏感性分析结果Fig.3 Analysis results of n1 value sensitivity

4.2 网联辅助驾驶车队规模对通行能力的影响

针对情景二，根据式(17)，令P1取值为0时，分析CRV车辆在不同渗透率下，CRV车队规模对混行交通流通行能力的影响.

计算得到取不同P2、n2值下交通流最大流量变化情况，如表4所示.

表3 不同n1、P1值下最大流量增加率

表4 不同n2、P2值下最大流量增加率

分析表4数据知，在情景二中，当P2≤0.3，n2>5辆时，最大流量增加率变化量低于0.1%；当P2>0.3，n2>7辆时，最大流量增加率变化量低于0.15%，故当n2取值为5～7辆时，通行能力提升效果最为显著，且P2值为1时，通行能力不受CRV车队规模的影响.

4.3 混有两种车队规模对通行能力的影响

针对情景三，根据式(17)，令P1和P2均不为0且n1和n2取不同值时，交通流最大流量变化情况，如表5～表8所示.

表5 P1=P2=0.3时,不同n2、n1值下最大流量增加率

表6 P1 =0.3且n2=5时,不同n1、P2值下最大流量增加率

表7 P1=0.3且P2=0.3时,不同n2、n1值下最大流量增加率

表8 P2=0.3且n1=8时，不同n2、P1值下最大流量增加率

分析表5数据知，当P1及P2一定时，改变n2并不影响n1的最优取值范围；同理分析表7数据知，P1及P2一定时，改变n1不影响n2的最优取值范围；分析表6数据知，P2不影响n1的最优取值范围；分析表8数据知，P1不影响n2的最优取值范围；结合表3及表4可知，当P1+P2=1时，通行能力与n1及n2的取值无关，此时通行能力仅与P1及P2的取值有关.

4.4 数值仿真

基于Matlab软件进行数值仿真试验，对一条随机分布100辆各种类型车辆的单车道路段，假设CACC车队规模n1=8，CRV车队规模n2=5.分别对上述三种场景进行数值仿真试验，仿真步长为0.01 s，同时考虑到网联车队与传统车辆相对位置随机分布，在每个渗透率下仿真3次，统计不同渗透率下，通行能力的均值.针对场景一，设n1=8，验证不同P1值时，通行能力变化情况；针对场景二，设n2=5，验证不同P2值时，通行能力变化情况；针对情景三，令n1=8，n2=5，P1=0.4时，验证不同P2值时，通行能力变化情况.每种场景下的理论值与仿真结果均值分别如表9～表11所示.

可以看出，仿真结果与理论值基本吻合，验证了理论推导的正确性.

表9 n1=8时，不同P1值下通行能力仿真结果Tab.9 Simulation results of capacity under different P1 values when n1=8

表10 n2=5时，不同P2值下通行能力仿真结果Tab.10 Simulation results of road capacity under different P2 values when n2=5

表11 不同P2值下通行能力仿真结果(n1=8,n2=5,P1=0.4)Tab.11 Simulation results of road capacity under different P2 values (n1=8,n2=5,P1=0.4)

综上所述，当P1与P2之和不为1时，在混行交通流中，CACC车队以车队规模为7～9辆且CRV车队以车队规模为5～7辆时，通行能力提升效果显著，当继续增加车队规模时，虽能提升通行能力，但此时通行能力提升效果受车队规模的影响较小.

5 结论

1)针对混有CACC车队及CRV车队的混行交通流，分析了两种网联车队在混行交通流中可能存在的9种跟驰模式，并建立了能够准确描述这9种跟驰模式的解析表达.提出了混有两种类型网联车队的混行交通流基本图模型，所提混行交通流基本图模型可有效分析两种网联车队规模以及两种网联车辆渗透率对混行交通流通行能力的影响.

2)在混行交通流中，CACC车辆与CRV车辆渗透率之和不为1时，CACC车队以车队规模为7～9辆且CRV车队以车队规模为5～7辆时，通行能力提升效果最为明显；当CACC车辆与CRV车辆渗透率之和为1时，通行能力与车队规模无关，而与CACC车辆与CRV车辆渗透率有关，且CACC车辆渗透率越大，通行能力越大.

3)车路协同环境下网联车队的跟驰模式将发生变化，其对混行交通流通行能力的影响将与车路协同模式紧密相关，因此，分析不同车路协同模式对混行交通流通行能力的影响将是下一步的研究方向.