基于深度学习和粒子滤波的公交车到站时间预测
安宇航,马继辉,刘慧勇,纪安琪
(1.北京交通大学 交通运输学院,北京 100044;2.北京信息科技大学 信息管理学院,北京 100192;3.青岛市市政工程设计研究院有限责任公司,山东 青岛 266000)
公交车到站时间是旅客重要的交通信息之一.准确地预测公交车的到站时间,对于减少乘客的等候时间和增强公共交通的吸引力具有重要意义.为了准确地预测公交车的到站时间,许多学者进行了大量研究[1].
历史趋势法首先应用于预测公交车的到站时间.该方法简单易行,适用于交通条件变化不大的公交线路.当交通状况复杂时,预测精度会降低.为了提高预测精度,探索历史数据之间的内在逻辑,采用时间序列分析方法[2-3]对公交车的运行时间进行短期预测.研究发现,公交运行过程受站点间距、乘客数量、信号灯数量、天气状况、实时交通状况等因素的影响.为了探索各种因素与公交车运行时间的相关性,许多学者提出并应用了变量衰减预测法和统计回归预测法[4-5].卡尔曼滤波(Kalman Filtering,KF)方法可以与状态方程和测量方程相结合.利用实时到站数据,采用递推法预测下一站的到站时间.由于其良好的灵活性和高效性,卡尔曼滤波在公交车到站时间预测领域得到了广泛的应用[6].在此基础上,许多学者根据实际情况将这些方法结合起来,充分利用每种方法的优点对公交车的到站时间进行预测[7-8].预测结果表明,融合方法比单一方法具有更高的预测精度,适用性强.但是,它们有局限性,即不能适应和预测非线性和非高斯复杂交通系统[9],并且实时性较差.
随着粒子滤波技术的进一步发展,已经应用于交通领域[10],如从卫星图像进行道路追踪[11],交通状态估计[12-13].粒子滤波不受噪声模型、非高斯和非线性时变系统模型的限制,具有比卡尔曼滤波更高的精度.目前,粒子滤波技术在公共交通领域基本用来预测公交线路的状态[14-15],也有学者将它运用到公交车辆到站时间预测[16].近年来,随着人工智能技术的发展,深度学习也逐渐被应用在交通预测领域[17-19],在公交车辆到站时间预测中LSTM(Long Short-Term Memory)方法运用的居多[20-21].但单一使用LSTM和粒子滤波方法的平均绝对误差在2 min,预测精度还有待提高.
本文结合深度学习和粒子滤波的优缺点,试图建立一种基于深度学习和粒子滤波的公交车辆到站时间预测模型,并通过实例进行了验证.LSTM模型和粒子滤波算法的优缺点互补,该算法能够降低LSTM模型在进行预测过程中很容易陷入局部最优与过度拟合现象出现的概率;解决了粒子滤波再进行预测时不能客观地反映公交车辆到达各个站点的情况.在预测公交到站时间的领域中,该模型的设计有很好的鲁棒性.本文作者充分分析了公交车到站时间的影响因素,并对采集数据进行归一化处理,作为模型的输入变量进行输入.验证表明,该模型具有较高的预测精度,能够有效减少乘客的候车时间,合理安排换乘,提高公交企业的服务水平和运营效益.
1 模型介绍
1.1 LSTM模型
LSTM是一种特殊的RNN架构,最早由Hochreiter等[22]提出.典型的RNN结构见图1.神经网络层A在t时刻,xt处查看输入,并输出一个值ht,通过一个循环让时间序列信息从一步传递到下一步.RNN的内部循环也可以看作是同一网络的多个副本,每个副本将一些信息传递给其后续节点,最后输出值为hT.LSTM与RNN具有相同的链式结构,但重复模块具有不同的结构.LSTM不是一个单一的神经网络层,而是有4个以特殊方式交互的层.LSTM的重复模块见图2.

图1 RNN基本结构图Fig.1 RNN basic structure diagram
LSTM重复模块中的计算步骤如下:
步骤1 “遗忘门”的sigmoid层决定从单元状态中丢弃哪些信息.查看上一时刻的输出ht-1和当前输入xt,并为上一单元状态Ct-1中的每个维度输出一个决策.输出ft的计算式为
ft=σ(Wf·[ht-1,xt]+bf)
(1)
式中:ft为t时刻的遗忘门状态值;Wf为权重矩阵;bf为偏置矩阵;σ为激活函数.
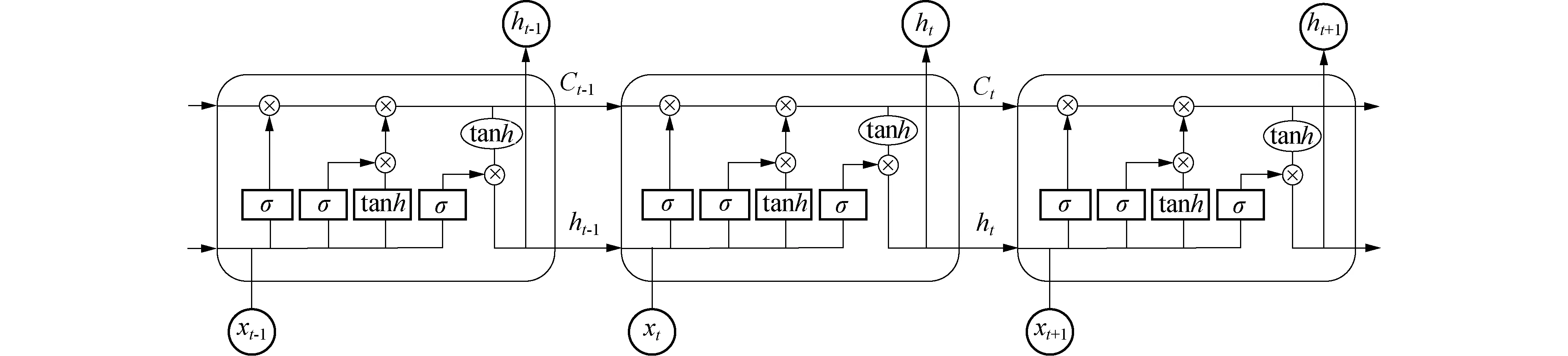
图2 LSTM的重复模块Fig.2 Repeating module in LSTM
步骤2 LSTM决定在单元状态中存储哪些新信息.“输入门”的sigmoid层决定更新哪些值.tanh层输出一个新候选值的向量,生成候选记忆.LSTM 更新单元状态,从旧的单元状态Ct-1变成新的单元状态Ct中.过程计算为
it=σ(WI·[ht-1,xt]+bI)
(2)
(3)
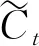
步骤3 将之前的单元状态Ct-1进行更新为
(4)
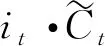
步骤4 最后由LSTM计算输出. “输出门”sigmoid层决定输出单元状态的哪一部分.单元状态通过tanh层,两者相乘得到一个新的单元状态,即为输出结果ht.计算的数学形式为
ot=σ(Wo·[ht-1,xt]+bo)
(5)
ht=ot·tanh(Ct)
(6)
式中:ot为输入值经过sigmoid函数后输出的状态;Wo为权重矩阵;bo为偏置矩阵.
1.2 粒子滤波
粒子滤波是利用大量随机样本和蒙特卡洛模拟技术来完成偏差递归滤波的过程.其基本思想如下:首先,选择一个重要概率密度,并进行随机抽样,得到具有相应权重的随机样本.其次,根据状态观察,调整粒子的权重大小和位置.然后,这些样本用于近似状态的后验分布.最后,取样本集的加权和作为状态估计值.
离散时间非线性状态方程和观测方程分别为
Xj=f(Xj-1,Wj-1)
(7)
Zj=h(Xj,Vj)
(8)
式中:Xj、Zj分别为状态变量、测量变量;Wj-1为过程噪声;Vj为观测噪声;f(x)为当前时刻状态与前一时刻状态之间的映射函数;h(x)为测量结果与当前状态之间的映射函数.
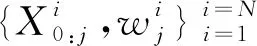
(9)
式中:q为重要性密度函数.
SIS的一个常见问题是粒子退化.本文提出了随机重采样方法来解决这个问题,随机重采样可以随时进行,但频率过高的重采样会增加计算负担,频率过低的重采样又会降低效率.因此,有必要定义一个重采样有效性的度量方法来计算有效样本的大小.这个衡量标准用来确定粒子的退化程度.本文采用相对效率Neff来衡量重要性采样造成的退化程度.Neff计算式为
(10)
粒子过多会增加算法的运行时间,降低算法的实时性能.如果粒子数量太少,粒子会严重退化.根据式(9),本文探讨了重采样标准.如果Neff满足Neff<2N/3,则需要重采样;否则,算法将进入下一步,不重采样.因此,不需要每次都进行重采样.根据样本情况,算法可以自适应地决定是否重采样,降低算法的复杂性.
2 公交车辆到站时间预测模型
2.1 公交车到站过程分析
首先,公交车从起始站出发,按规定的路线行驶.然后,公交车经过不同的公交车站和交叉口.当公交车到达车站时,公交车将进入公交车站,停下来等待乘客上下车,然后离开公交车站.最后,公交车运行全线并到达终点站.公交车的运行过程见图3.

图3 公交车运行过程Fig.3 Bus operation process
本文旨在准确预测公交车辆到站时间.Tj-1为到达j-1站的时间;tj-1为j-1站的停车时间;Tj-1,j为从j-1站到j站的区间运行时间;Tj为j站的实际到站时间.利用Tj-1,tj-1和Tj-1,j建立了公交车到站时间预测模型,去预测到达j站的到站时间.Tjj为j站的预测到达时间.j站到站时间的实际时间和预测时间,两者之间存在一定的误差.误差ΔTj为
ΔTj=Tjj-Tj
(11)
当误差减小时,实际值更接近预测值,模型更准确.
2.2 基本影响因素分析
2.2.1 车辆实时位置与速度
公交车辆到站时间的基本影响因素为实时位置、速度和历史的数据(由GPS数据获取),其他辅助数据包括:公交车牌号、线路编号、线路名称、运行时间、运行位置(经纬度)、运行速度、进出站时间.
2.2.2 GPS数据处理
为了提高预测模型的精度和计算车辆每秒的定位信息,需要对GPS数据进行线性插值.按时间顺序收集了一组GPS定位点{P1,P2,…,Pi,Pj,…,Pn},(1≤i≤n,j=i+1).点Pi有很多属性,包括时间ti、经度坐标xi、纬度坐标yi和速度vi等.相邻两个坐标点的线段定义为PiPj,长度为Lij.假设两个数据点的运行为均加速或均减速.以Pi为起点,得到了一个新的线段集{Pi+1,Pi+2,,…,Pi+k,…,Pj-1}(1≤k≤m).线段PiPi+k的长度为Li,ik.新线路集的条件为
dij=Lij/m
(12)
m=tj-ti
(13)
Li,ik=kdij
(14)
(15)
vi+k=vi+aij·k
(16)
式中:dij为插值距离;aij为两点之间的加速度;k为插值点的一个变量,1≤k≤m,m为时差,也即为在线段PiPj中最大的插点数量.
将插值{Pi+1,Pi+2,,…,Pi+k,…,Pj-1}加到原集合{P1,P2,,…,Pi,Pj,…,Pn}(1≤i≤n,j=i+1).可以每秒近似地计算出公交车位置信息,处理效果见图4.
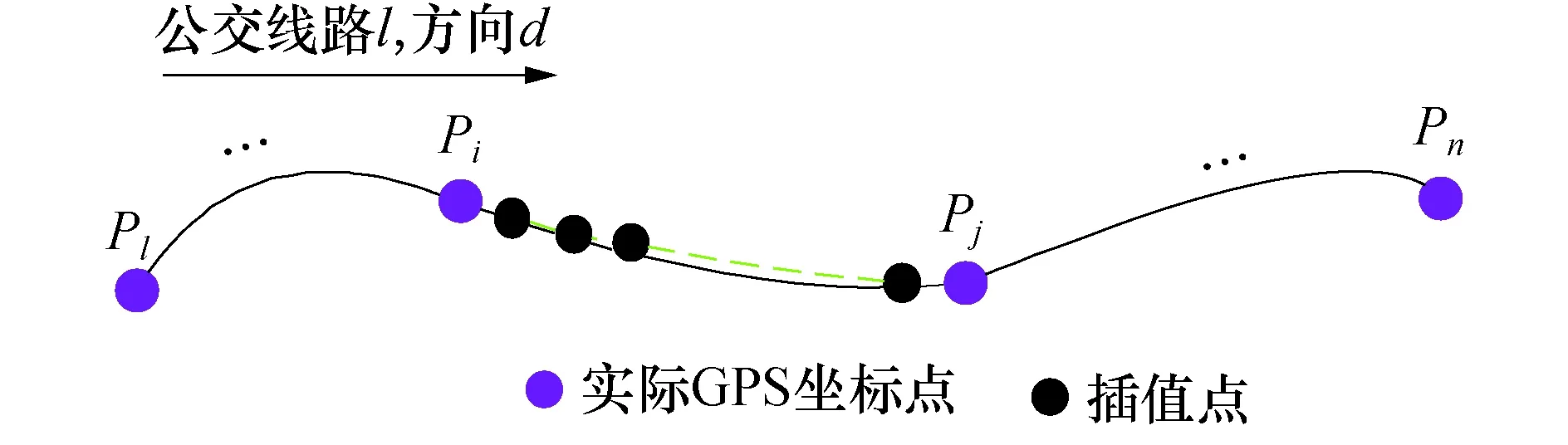
图4 数据插值效果Fig.4 Diagram of the data interpolation effect
2.3 其他影响因素分析
公交车具有常规定点运行特性.公交车在运行过程中受到各种影响因素的影响,如天气、路况[23]、交叉口、驾驶员、乘客和交通突发事件等[24].为了更加准确地预测公交车的到站时间,需要对公交车到站时间的影响因素进行选择,建立预测模型.
2.3.1 天气影响
在交通运输中,天气状况的好坏会影响车辆的运行.在天气恶劣的情况下,为了保证安全行驶,车辆的行驶速度往往会很慢,从而导致车辆的运行速度很慢,公交车的到站时间会延迟.如,在雨雪天气,降低道路的摩擦系数,导致车速变慢;在雾霾天气,由于能见度变低,车速也会相对较慢.本文基于降雨/雪量多少和雾(霾)因素将天气状况分为4个等级,见表1.

表1 天气状况
2.3.2 道路等级
公交车的运行时间也会受到道路等级的影响.不同等级的道路的设计车速不同,导致运行时间也会出现差异,从而影响公交车的到站时间.如,城市快速路和主干路车道数多,设计车速高,公交车的运行时间就会缩短;而在次干路和支路,设计车速较低,公交车的运行时间相对较长.根据城市道路要求[25],本文将道路等级分为4类,见表2.

表2 道路等级
2.3.3 公交车站台类型
公交车站台类型主要对公交车的在站台停靠时间和进出站时间造成影响,从而影响公交车的运行时间.本文将公交车站台分为3种类型,见表3.

表3 公交车站台类型
2.3.4 交叉口和地铁站
公交车站台距离交叉口过近或附近有地铁站也会对公交车的运行状态产生影响.若公交车站台100 m附近内有交叉口则设为1,无交叉口则设为0;若距离公交站点200 m附近有地铁站点则设为1,无地铁站点则设为0.
2.3.5 工作日和非工作
工作日相对于非工作日由于出行需求较多,高峰时段较为拥堵,会对公交车的运行时间产生影响.本文将工作日设为1,非工作日设为0.
2.3.6 公交车站点上下车人数
上下车人数直接影响到公交车在站点的停靠时间,从而影响公交车的运行时间.通常在高峰时段公交车的发车频率相对较高,乘客在公交站点的等待时间会减少,公交车站点汇聚的乘客相对较少,公交车的上下车人数相对减少,上下车时间也会对应缩短.
2.4 公交车到站时间预测模型
本文预测公交车到站的场景为:假设距离乘客最近的公交车在j-1站和j站之间,而乘客此时在j+a站点,想要知道距离自己最近的公交车合适到达j+a站点,即需求站点的时间.
本模型为LSTM+粒子滤波串联模型:LSTM的输入变量为公交车牌号、线路编号、线路名称、运行时间、运行位置(经纬度)、运行速度、进出站时间、天气、道路等级、公交车站台类型、交叉口和地铁站、是否工作日和公交车站点的上下车人数.输出变量为M个预测到站时间.将LSTM的输出变量作为粒子滤波的粒子,通过粒子滤波进一步选择最优的预测值.
LSTM-粒子滤波模型的流程图见图5.
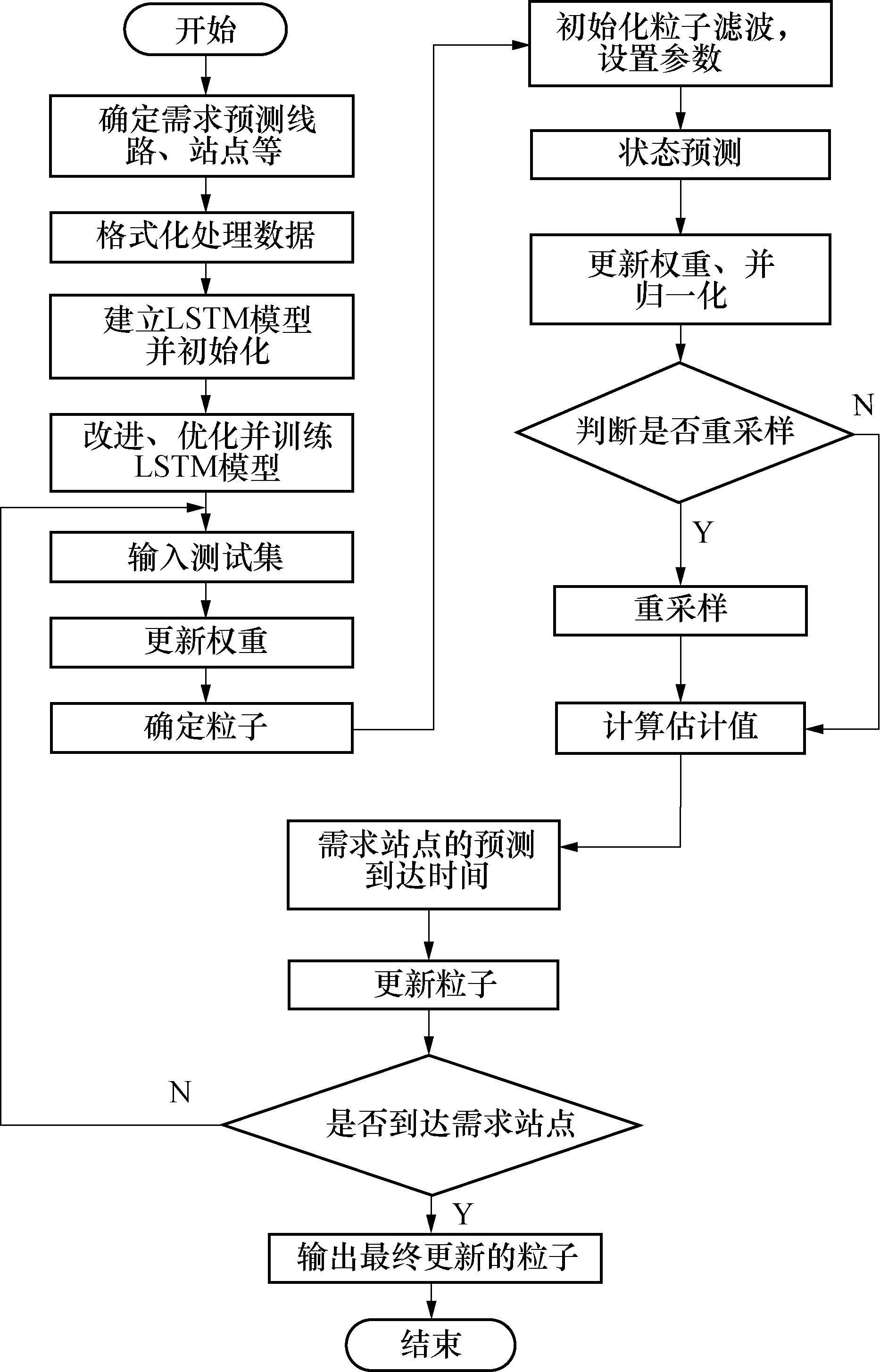
图5 LSTM-粒子滤波模型算法的流程图Fig.5 Flow chart of LSTM and particle filter model algorithm
具体的步骤为:
步骤1 将数据分为两部分“训练集和测试集”,确定LSTM输入变量.
步骤2 由经验确定LSTM每个参数的大致范围,通过Keras库建立M个LSTM模型,将模型进行初始化.
步骤3 将训练集输入到不同参数的LSTM模型中进行训练,将训练集的预测结果和实际结果进行对比,通过损失函数和优化函数等对权重进行不断地更新.
步骤4 再将测试集输入到训练好的M个LSTM模型中,得到所需站点m的M个预测到站时间.
步骤5 粒子滤波调整过程:把LSTM的预测过程作为粒子滤波的状态转移过程,将M个LSTM模型产生的M个预测到站时间作为粒子,不断对其进行权重更新和重采样,最终输出误差最小的结果.
①初始化参数.对粒子滤波算法参数进行初始化,如初始迭代变量j为0,粒子数为N.
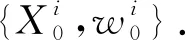
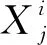
(17)
⑤判断是否进行重采样.如果Neff满足Neff<2N/3,则进行重采样,将复制权值大的粒子,得到新的粒子集;否则,不进行重采样进入下一步.
⑥估计状态值.状态j在式(18)中估计.然后,更新后验概率密度函数.
(18)
步骤6 判断公交车是否到达需求站点.若j=j+a,算法结束,证明公交车到达需求站.否则,j=j+1,转到第步骤4.
3 案例分析
3.1 模型的参数选择
本文借助Python中的Keras库进行LSTM网络的搭建;LSTM网络的结构层数为两层;输出维度为一维;时间步长[2,4];迭代次数为200;初始学习率为0.000 1;一次性输入到神经网络中训练的数据个数为30;隐藏层神经元个数为13.粒子滤波的权重计算式为
(19)
式中:Zk为观测时间;ξ为式(8)中Vk的标准差.
3.2 数据的选择和处理
本文选取北京市公交300路、345快线、438路和464路4条典型的公交线路作为研究线路,300路和345快线为长线路,464路是短线路,345快线、438路和464路是多边形线路,300路是环形线路且经过旅游区和贸易区,345快线、438路和464路经过大学和居民小区.这4条线路具有普遍的代表性.本次实验中4条线路的公交站点数量见表4.

表4 公交站点
选取连续30 d(工作日和非工作日)的数据,其中300路共有3 678车次的数据;345快线共有2 854车次的数据;438路共有2 989车次的数据;464路共有3 245车次的数据,按时间分为早高峰(7:00—9:00)、平峰(10:00—12:00)、晚高峰(16:00—18:00)三类,采取1—27日为训练集数据,28—30日为测试数据.4条线路的公交站点示意图见图6.
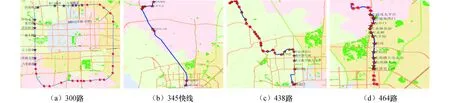
图6 样本线路中的公交站点信息Fig.6 Bus stop information in the sample route
3.3 选择误差指数
模型的预测效果用平均绝对误差MAE来衡量[26],可以直接反映预测值与实际值之间的偏差.
(20)
3.4 模型预测结果
4条典型线路的预测结果见图7.选取28、29、30日数据用于检验模型的预测效果.这4条线路的预测结果表明,平均绝对误差均在80 s内,预测结果准确,满足公交车到站时间预测的要求.结果表明,LSTM-粒子滤波模型适合预测各种类型公交线路的到站时间,且效果显著.
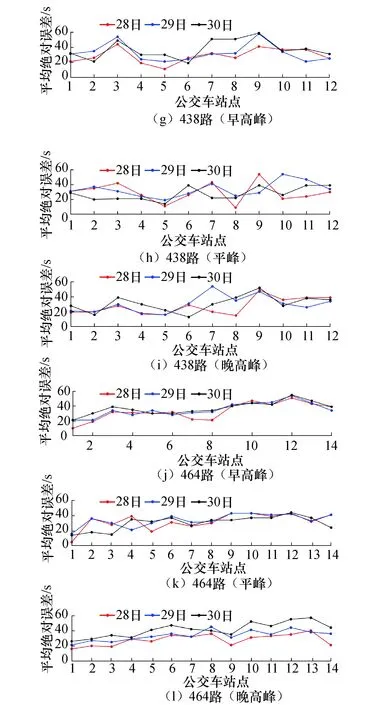
图7 4条典型线路的预测结果Fig.7 Predicted results of four typical lines
3.5 效果对比分析
为了进一步说明LSTM-粒子滤波模型的适用性和准确性,与LSTM和粒子滤波单独使用时进行比较.以3月29日为例,采用3种方法预测4条公交线路在早高峰、平峰和晚高峰的公交车到站时间.3种预测方法的结果对比见图8.
由图8可见,对于4条实验线路,LSTM-粒子滤波模型的平均绝对误差小于LSTM和粒子滤波单独使用时的平均绝对误差.LSTM-粒子滤波模型的平均绝对误差仅在10~80 s的小范围内波动,而LSTM和粒子滤波算法单独使用时的平均绝对误差波动范围为30~120 s.因此,应用LSTM-粒子滤波模型预测公交车的到站时间具有更高的精度和准确度.
平均绝对误差MAE见表5.由表5可见,LSTM-粒子滤波模型的平均绝对误差低于LSTM和粒子滤波算法单独使用时的平均绝对误差.总体来看,各线路的平均绝对误差均小于80 s,满足公交车到站时间预测的需求.早高峰时,LSTM-粒子滤波模型的平均绝对误差为37.98 s,LSTM的平均绝对误差为49.44 s,粒子滤波的平均绝对误差为59.39 s,LSTM-粒子滤波模型与LSTM、粒子滤波相比分别增加了17.11%、31.00%.同样,与LSTM和粒子滤波相比,在平峰期,LSTM-粒子滤波模型的平均绝对误差分别增加了16.24%、33.71%.在晚高峰期,则分别增加了23.73%、34.87%.在对公交车辆到站时间预测时,LSTM-粒子滤波模型的预测精度都高于LSTM和粒子滤波的单独运用.因此,LSTM-粒子滤波模型可以更有效地预测公交车的到站时间,具有较好的准确性.
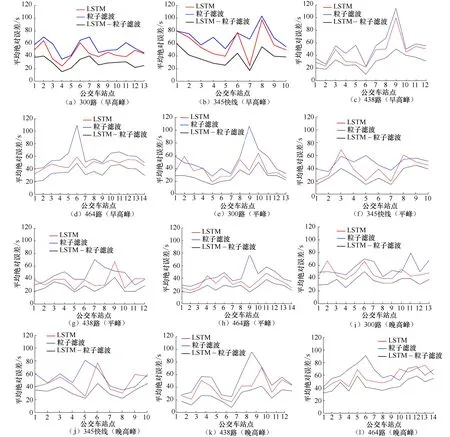
图8 3种预测方法对比Fig.8 Comparison of three prediction methods
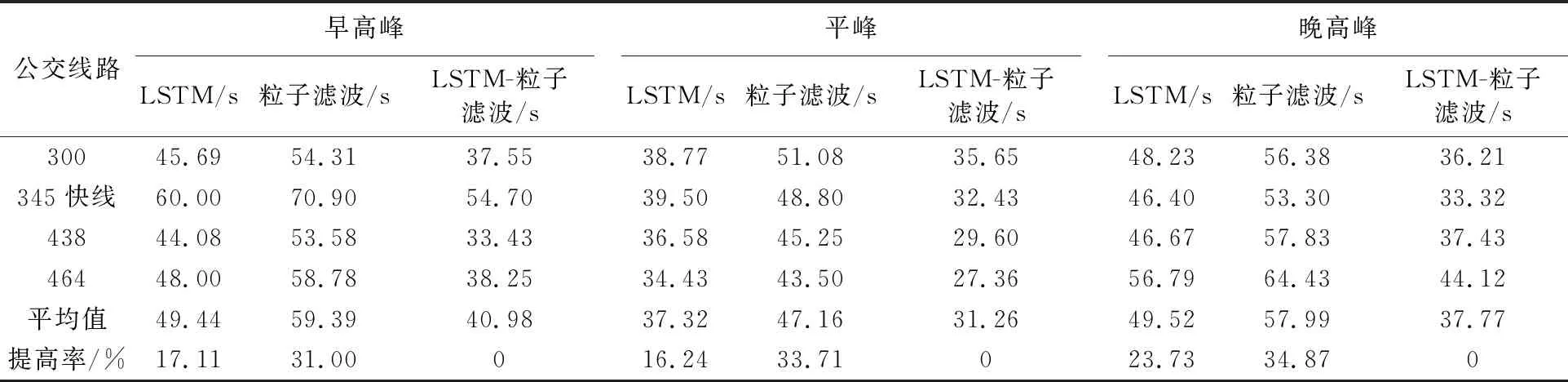
表5 线路的平均绝对误差
4 结论
1)结合LSTM模型和粒子滤波的优缺点,建立一种基于深度学习和粒子滤波的公交车辆到站时间预测模型,并对其中的LSTM模型进行了改进,避免其在进行预测时陷入局部最优解,从而降低预测精度.
2)分析了公交车到站时间的影响因素,选择GPS数据、天气、道路等级、公交车站台类型、运行方向、交叉口和地铁站、是否工作日和公交车站点的上下车人数,并对采集数据进行归一化处理,作为模型的输入变量,有效地提高了模型的预测精度.
3)对北京市4条典型公交线路进行分析和验证,选取平均绝对误差MAE作为评价指标.结果表明,LSTM-粒子滤波模型能更准确地预测公交车的到站时间:平均绝对误差在80 s以内.并与LSTM和粒子滤波单独使用时进行比较:LSTM-粒子滤波模型在早高峰的平均绝对误差分别增加了17.11%、31.00%;在平峰期,平均绝对误差分别增加了16.24%、33.71%;在晚高峰期,则分别增加了23.73%、34.87%.该模型具有较高的预测精度,能够有效减少乘客的候车时间,合理安排换乘,提高公交企业的服务水平和运营效益.
今后,将进一步探索与公交车运行状态相关的影响因素,运用更科学的方法对LSTM参数进行设置,提高预测的准确性.

