把握课后延伸，有效渗透数学思想

邹雨珊

摘 要：在“双减”背景下，如何设计课后作业既能有效地减轻学生过重的负担，又能体现思维成长成为当下学界高度关注的教育话题。文章在对单元整体内容分析的基础上，设计出发展学生“空间观念”“应用意识”及“创新意识”的探究性作业，让学生在兴趣高涨的前提下高效地完成课后延伸，有效地渗透数学思想。

关键词：探究性作业;创新意识;数学思想

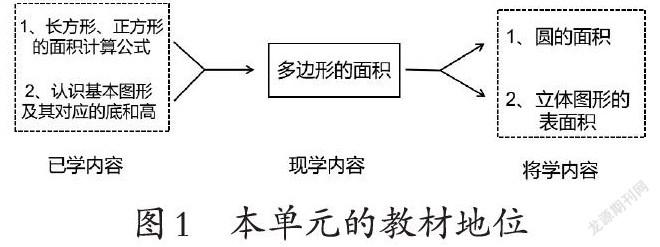
人教版五年级上册“多边形的面积”是小学阶段较为系统地学习几何图形面积计算的重要内容，同时也是能让学生充分感受和积累转化经验的学习材料。在分析该单元的教学内容和教学目标的基础上，设计有趣、有效的实践性作业，实现知识的有效延伸和数学思想的有效渗透。

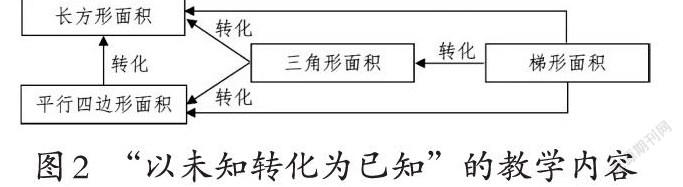
一、“以未知转化为已知”的教学内容

（一）承前启后的教材地位

本单元是以长方形计算为基础，以图形内在联系为线索，以未知转化为已知的基本方法开展学习的，发展空间观念的重要载体，更是后续推导圆的面积和立体图形表面积的重要依据。

（二）重视操作体验，渗透“转化”数学思想

教材以转化思想探索图形面积的计算方法，而组合图形和不规则图形更是这些基本图形的综合运用。所以在教学中要突出转化思想，让学生通过动手操作，将所研究的图形转化为熟悉的图形，促进知识的迁移和学习能力的提高。

（三）切忌固化学生思维

推导多边形面积计算公式有许多途径与方法。例如在探究梯形面积计算公式中，可以鼓励学生将梯形的面积分成两个三角形，或分成一个平行四边形和一个三角形，还可以用两个一样的梯形拼成一个平行四边形等，所以教师在教学中要注意放手让学生自主探究，发散学生的思维，提高学生的应用意识和创新意识。

二、发展空间观念的教学目标

教师不仅需要引导學生探索和掌握平行四边形、三角形、梯形的面积公式，会计算组合图形和不规则图形的面积，而且需要在学生进行观察、猜想、验证等操作活动中，渗透平移、旋转、转化等数学思想，发展合情推理能力，促进学生空间观念的发展，渗透估测意识，让学生了解解决问题方法的多样性，培养学生的应用意识和创新意识。

三、指向思维发展的探究性作业

基于以上分析，教师有必要做好课堂教学中的延续和补充，设置发展学生“空间观念”“应用意识”及“创新意识”的探究性作业，促进学生综合能力的提高，进一步深化教学目标。

（一）问题式前置性作业，发展“空间观念”

本单元各图形面积计算公式的推导都要转化为熟悉的图形。所以在课前融合美育，布置问题式前置性作业，让学生在问题的引导下先自主探索，后课堂展示。这样不仅提高课堂的效率，而且增强了学生的自信心和兴趣。例如：本单元在学习三角形的面积之前，为了让更多学生充分理解“转化”的数学思想方法，可以先布置问题式的前置作业：

学生在问题的引导下，回顾平行四边形面积推导的过程，并通过拼一拼、摆一摆的方法尝试将该三角形转化成熟悉的图形，并用已学过的图形推导出三角形的面积公式，最后在课堂上展示出来。这一系列的操作过程中，学生初步体验了图形的平移、旋转以及转化的数学思想方法，促使空间观念得到进一步发展。

（二）多元化操作实践，渗透“应用意识”

1. 推理达人

本单元以图形内在联系为线索，将未知转化为已知。学习完该单元，教师可让学生利用同样的方法探究特定圆的面积，以此渗透学生的应用意识，为后续推导圆的面积公式打下基础。例如可以设定以下作业：一个能通过数方格测量的特定圆，而另外一个是利用剪一剪、拼一拼、平移和旋转等方法，将其转化成熟悉的图形后再求面积，让学生在推理中收获成功的体验。

2. 估算达人

为了让学生积累活动经验，培养学以致用的学习态度，在学习完本单元后，教师可以布置学生采取实际行动量一量、算一算家里室内的面积，培养学生数学应用意识和渗透学生估算思想。

3. 小讲解员

“理”越辩越明，“道”越论越清。教师可布置学生借助思维导图、错题本或某一道题拍摄讲解视频，要求学生讲解分析过程，让学生在表达过程中加强逻辑思维训练。例如面对“将一个平行四边形拉成长方形，面积是否变大，周长是否没变”这个问题，学生可以通过数形结合分析：将平行四边形拉成长方形后，底和长相等，而高拉成宽后变长了，所以面积会变大，而周长依旧是原来的四条边，所以周长不变。学生说的过程就是梳理的过程，也是学生自我审视的过程，更是发展“应用意识”的过程。

（三）发散思维，提升“创新意识”

1. 分层实行以图导思

思维导图在数学教学中的运用，是激发学生自主学习、提升学生创新意识内在要求，但班级内学生的知识水平和接受能力是有差异的，所以以图导思也要考虑因材施教。例如：在该单元学习结束后，部分学生只需设计出运用不同公式计算出不同图形面积的思维导图;而对于善于总结的学生，则要求他们将每一个知识点自主巧妙地链接起来，将多边形面积计算公式进行关联，以此转化学生思想和提升学生的创新意识。

2. 发散思维求组合图形面积

在探索组合图形面积的计算时，教师要相信学生的创造力，并在教学中启发学生从不同的角度发散思维、勇于创新。例如教材中例4需要求解房子侧面墙的面积，学生在课堂上通过自主探究汇报出常规的割补方法，在课后延伸中可以鼓励学生思考其他的方法——先将组合图形分割成三角形和正方形，将上面的三角形变形为同底等高的三角形，然后把整个图形转化成了一个完整的梯形。课后给予学生足够的鼓励和充足的时间去思考，发散学生的思维，让学生获得成功的体验，从而提升学生的创新意识。

把握课后延伸，设计实践性作业，留有充裕的时间让学生自主探索，激发学生乐于学习的积极性，拉近知识与生活的距离，让学生的空间观念、应用意识和创新意识得到切实、有效的发展。

参考文献

[1]丁玉成.有效衔接 实现思维跨越——人教版五年级上册“简易方程”单元探究性作业设计[J].教学月刊小学版（数学），2021（10）.

[2]徐平惠.小学高年级数学课后探究性作业设计[J].考试周刊，2019（77）.

[3]钱建兵.思想贴近儿童 方法引领课堂 活动提升能力——五年级上册“多边形的面积”教材解析与教学建议[J].小学数学教育，2015（Z4）.

[4]刘善娜.单元整体视角下小学数学探究性作业的设计[J].教学月刊小学版（数学），2021（10）.