整数除法与编程融合的创新实践

李海国

整数除法计算教学需要把学生从程序的操作引领到以理解除法运算本质为基础的概念理解中，借助程序设计融合整数除法与连减，沟通知识的内在联系，这就需要对计算教学的教学流程进行创新，从运算的本质上深入思考设计程序算法，从教学支架上构思帮助学生实现水平提升。

计算教学到底能给学生带来什么？考试中往往以计算题来考察学生是否掌握，如果仅仅以让学生能正确计算为指标来衡量计算教学的话，相当于把学生看成了“计算器”，降低了计算教学的价值。在实际的教学中，大多数教师还是坚持让学生多练，以能否正确计算为最主要目标来进行教学，如何能改变现状，在计算教学中实现更高的价值追求呢？本文以人教版四年级上册第六单元除法是两位数的除法《例7》一课为例，开展教学的创新实践，探索计算教学如何实现学生更高的发展。

一、教材的基本教学流程

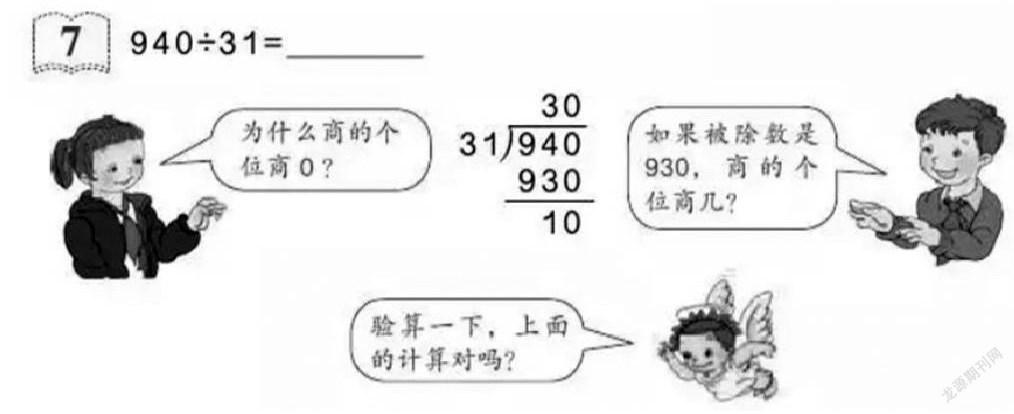
教材的第一项主要内容是教学例7，题目是940÷31=，教材图片中的一位女学生说：“为什么商的个位商是0？”，另一位男学生说：“如果被除数是930，商的个位是几？”小精灵说：“验算一下，上面的计算对吗？”;通过三个问题让学生通过讨论理解为什么要商0，一是不够商1时要商0占位，二是0除以31商为0，进而在验算中，验证商的正确性。

第二项内容是归纳计算方法，让学生比较除数是一位数和二位数的计算方法有什么不同，进而归纳出除数是两位数除法的一般方法，也就是计算的程序步骤。至于为什么是这样的程序，缺少解释说明。实际教学中多数教师也是按这样的环节来教学，追求会算、算对。

二、教学过程的重新设计

在解决实际问题中，学生经常会遇到除数是三位数、甚至四位数的除法，学生往往束手无策，表示教材没有教过，这节课也确实是整数除法的最后一课，为什么会出现如此情况？就是因为教材在这里没有适当地迁移，没有让学生理解整数除法的可迁移的本质，到底要从哪里商起？为解决此问题，进行了创新设计。

教学目标：

（一）利用交流、举例、猜想理解商个位商0的本质取决于什么。

（二）利用竖线和程序沟通除数是不同数位除法的联系。体会从高位除是连续减一个除数的优化策略。

教学过程：

（一）出示情境

玩具店老板用640元在网上买21元的汽车模型，可以买几个？

（二）探索

1. 独立解答，并要证明自己做的是正确的，同桌交流想法。

2. 交流：你是怎么想的？有什么质疑？商的个位不写可以吗？商1行吗？为什么要商0？

3. 用数线尝试：

教师引入一个一个减的方法，让学生逐步优化，为什么不一个一个减？

用减法表示，并与除法竖式比较，有什么联系？

设计意图：让学生建立整数除法与连减的直观内在的联系，优化连减的策略，为后续的编程，迁移到除数是多位数的除法做好铺垫。

4. 猜想：

猜想一：通过观察被除数个位上是0，商的个位一定是0，对吗？请寻找证据说明。

猜想二：被除数个位上不是0，商的个位上一定也不是0，对吗？寻找证据说明。

5. 总结：商个位商0与被除数的个位上是几，有必然的联系吗？思考与什么有关系？

设计意图：学生在是否商0时易受被除数的数字影响，有的学生一看到被除数上有0，就在其上面商0，为克服学生的刻板错误，在寻求证据交流中，建立商0与余数的非人为的本质的联系。

6. 编程：想要用电脑程序来解决所有整数除法的问题，你有什么想法和思考？

① 引导举例概括，不管除数是几位数，都可以一个一个来减。

② 让这生用程序来试一试。

③ 比较：200000000÷2，看人和电脑哪个快？为什么人算得快？有什么区别？

设计意图：通过程序设计任务来整合多位数的除法，教师举例除数是一位数、两位数、三位数，借助数线发现相同的地方，进而解释用这样的想法编写的程序。学生尝试后发现无论除数是几位数都能很快算出来，有的学生会感受到程序的优越性与自己的无力。基于此设计比较的环节，让人与电脑比赛，学生已经算出好长时间了但电脑迟迟没有计算出来，学生满心欢喜。这时让学生比较有什么区别，优化减的策略，从减一个除数到从减10n个除数，体会为什么除数是几位数就要从被除数的前几位商起的道理。

（三）总结

1. 你还想知道什么？

2. 程序中的彩蛋：电脑程序中有一个致命的漏洞，你能找出来吗？

教学感受：课上得挺快的，学生笑声不断，思维不断。学生眼中始终闪着智慧的火花，看着很是享受。在“找彩蛋”环节时，学生不断尝试，尝试除0时，电脑直接死机了，就不由自主地欢呼了起来。教师接着问为什么会这样，又勾起了学生探索的欲望，此时已经下课了，但没有一个学生着急下课，还在与同桌探讨自己的想法。

三、从理解除法本质上与编程融合

学生学习整数除法，从除数一位数到两位数，分了很多的知识点，从整数到试商、调商、有0的除法，无非都是在学习竖式计算的一种程序性知识，既然是程序性知识，就是有一定的步骤。如果让电脑用一个程序来解决所有的整数的除法，这个程序该如何，这就要从本质上来理解。不管是平均分还是包含除，都是连续减一个相同的数（除数）。平均分里，每次每份分一个，一次分掉一个除数，相当于一次从总数里减一个除数;包含除里，一次减一个除数，减几次，商就是几。不管除数是几位数，这个方法都是通用的，那就连续减除数，直到余数小于除數为止。

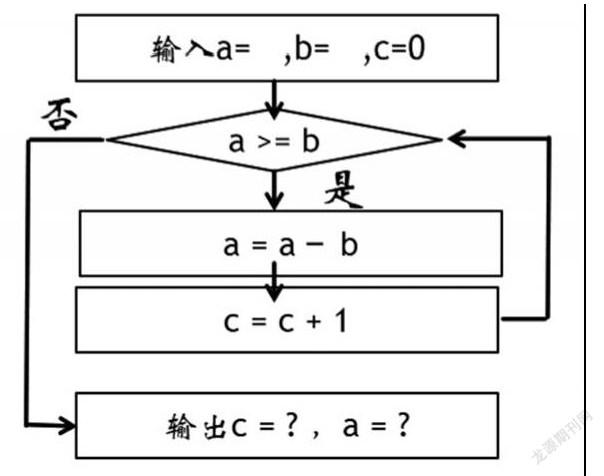
下面编的python程序，就是以除法本质的思考来设计的。当被除数大于或等于除数时，就从被除数a里减去除数b，同时c记为1。这时再循环到条件判断“a>=b”，如果成立，继续减，同时c再加1。一直这样循环，直到条件不成立时，减了多少次商就是几，这个数据就被c记录了下来，c就是商的值。

既然一个一个减通用，为什么还要学习竖式呢？因为一个一个减除数确实通用，但不实用，如果24000000除以2，一个一个减，要减一亿多次，所以在实践中人们进行了优化，即从10n个减数开始，直接一次先减108个2，有余的，再依次往下想，再减107个2，这个速度很快。这也就能解决为什么除数是两位数就要看被除数的前两位的意义，本质上就是从10n个减数开始，n就是被除数的位数，如被除数是四位数，先从一千个减数开始减，不够减时，再从一百个减数开减，依次从高向低。这样优化后减得就快了，与减法建立必要的联系，这样学生学习就融会贯通了。

四、从教学支架上支撑与编程的融合

要实现上面的融合创新，已经超越了学生的现有水平，就需要为学生搭建一个支架。一个是猜想，让学生通过两个猜想的验证过程中，寻求商个位是0的本质是什么，就是余下的数小于除数了。另一个是“数线”，研讨过程中，有的教师就提出了质疑，已经学了竖式，还要用数线，岂不多此一举吗？这是因为：

1. 它是直观支架，避免“空对空”，符合学生认知特点。

2. 利于探索除法的算理，在直观感受中，优化减除数的策略。

3. 基于理解的模型。

因为学生在某个水平上的问题不能解决的情况下，学习者会折回到低一级的水平上，重新去拓展目前仍不够充分的理解。也正是因为数线的支撑，学生通过电脑程序的对比，对除法的本质、计算方法的融合才能更进一步。

五、融合创新实践的思考

从这一案例中可以看出，学生是否有创新思维，关键是教师在教学上是否有创新思维。

1. 教师要尝试发散性思维。以原有的经验为基础，尝试从不同角度思考问题，不能同样的内容每次都是重复，要敢于做出不同尝试，哪怕失败了又何妨？正好从失败中吸取教训，改进后再实践。

2. 教师要尝试扩展式思维。将研究对象扩展，将除数位数、图象表征、程序表达等联系起来思考。不能见树只是树，要站到更高的高度，整体、全局、深入地看待问题，将教材呈现的内容进行扩展、补充，让学生的思维扩展，不仅能算除法是两位数的除法，也能扩展到除数是多位数的除法，理解运算的本质是相同的。

3. 教师要尝试与新技术进行融合。新的技术往往带来新的思考，结合学生课外常用的“海龟编辑器”，就可以将数学的程序性知识，通过编程来解决，两者互为促进，提升了学生的思维水平。

创新不易，哪怕是一丁点的改进，也是进步。敢于尝试不同的策略、不同的技术，不断思考，将之在数学的本质上进行融合，学生的思考也就會在活动中更加深入，教师的创新也就带动学生的创新，学生不仅知道为什么这样算，还能进行程序设计的创新，岂不比只能正确计算更好、更有价值！