多Agent的动态信念和知识推理

林 颖，卫 龙

(1.宁德师范学院马克思主义学院，福建 宁德 352100；2.安徽大学哲学学院，安徽 合肥 230039）

Agent（主体）是人类智能、动物智能和机器智能的统一模型[1]3。理性Agent具有知识、信念、愿望、意图和行为，如何对这些概念及其相互关系进行形式化是分析哲学、逻辑学和人工智能长期关注的课题。如何形式化地表征“动态信念和知识对单主体行为的影响”，国内外不乏这方面的逻辑模型。在多主体环境下，如何形式化地描述动态信念和知识对多主体行为的影响呢？本文构建的关于动态信念和知识的多主体逻辑（简记为BDL逻辑），试图回答这一问题。

一、引言

在20世纪，关于Agent研究主要集中在两个方面：一是知识和信念等信息方面；二是承诺和义务等动机方面。后来的发展主要包括：面向主体的编程、对理性主体进行形式化的BDI结构、对多主体系统进行形式说明和验证的逻辑、受限理性主体逻辑和认知机器人学、对理性主体（各个方面的）行动进行说明和推理的逻辑。以上这些主要研究了主体的信息和行动特征，而忽略了主体动机方面的特征。在随后的研究中，用以下内容对这些逻辑框架进行了扩展，包括：不确定性行动、认知测试和交际行动、模拟缺省推理行动[2]。执行行动的结果可以被定义为“行动的执行所导致的事件状态”[3]。

多位学者使用不同的方法研究了面向Agent的系统。在对主体和多主体系统进行研究和形式化时，经常用到逻辑方法，尤其是模态逻辑。在所有主体系统中，较为著名的具有模态特征的主体形式系统有：动态逻辑和认知逻辑的融合系统[4]、BDI系统[5]、KARO框架[6]、知识和信念的时态逻辑[7]、关于信念和更新的模态逻辑框架[8]、动态认知逻辑[9]。

在这些系统中，最为著名且应用最广的是BDI系统。BDI系统[5]认为：Agent是具有信念、愿望和意图（Belief-Desire-Intention，简称BDI）这三种心智态度的理性主体；信念是主体系统的信息内容；愿望是主体系统的动机状态；意图是主体系统的慎思内容。因此，BDI表征了主体的信息、动机和慎思状态。当慎思（deliberation）受制于资源时，这些心智态度决定了主体系统的行为，因而是达成适当或最优性能的关键[10]。主体行为可以看成是“由系统直接执行的时态逻辑说明”[11]。IRMA系统[12]和PRS-类系统[13]，都是对理性主体的BDI逻辑系统的不同实现。

BDI逻辑能够描述信念和知识对主体行为的影响，而BDI逻辑的基础系统是命题动态逻辑PDL（简称PDL）[14]。PDL逻辑有两种语言：程序语言和命题语言，能够对程序或行动进行推理。模态逻辑系统S5[15]能够对知识进行推理，公式□φ可以解读为“主体知道φ”。因此，对PDL中测试算子的语义和形式系统进行重新描述，并采用“能够对抽象行动和具体行动加以区分的”新的行为表示方法，就可以达到对多主体环境下的动态信念和知识建模的目的。这种新的测试算子被称为信息测试算子，可以用来把特定主体的信念和知识形式化为动态模态词。这种信息测试算子与K(D)45和S5这类系统中的“能够对主体的信念和知识进行形式化的模态词”类似。这种把PDL和S5进行融合后得到的逻辑就是本文重点研究的动态信念和知识的多主体逻辑（简称BDL），该逻辑是BDI逻辑的变种。

在哈瑞（Harel）等[14]、布拉克布恩（Blackburn）等[15]、斯密迪特（Schmidt）[16]和提西孔思科（Tish‐kovsky）[17]、张晓君[1]等文献的基础上，本文试图形式化地描述动态信念和知识与多主体行为之间的关系。其基本思路是：通过引入信念或者知识的确认行动，把主体的隐性信息态度（信念或者知识）进行显性化。信念（或者知识）确认行动是通过改进后的测试算子（即信息测试算子）进行建模。信息测试算子只具有确认信念或者知识状态中的公式的能力，不具有很强的确认当前世界所有真实性质的能力。

BDL逻辑语言具有较强的表达力，这种表达力主要是通过向主体信念中引入动态性来实现的，即把新的信息测试算子整合进主体信念中。虽然信息测试算子具有许多优点，但是对抽象行动和具体行动进行区分也是至关重要的，有了这种区分才能够对多主体间的合作与团队协同进行推理，而不仅仅是对单主体的推理[18]。

二、BDL逻辑的语言和语义

由于主体行为具有不可预测性，即必须反映系统的不确定性，这就要求其形式语义学是状态语义学。此外，要求主体具有智能，可以把简单的行动组合成复杂的行动。允许任意主体执行的行动称为抽象行动；抽象行动可以是原子行动也可以是复合行动。抽象行动只是主体可以执行的真实而具体的行动的名称。任何具体的行动总是与某个主体相关联，因为不同的主体可以以不同的方式执行（抽象）行动。

假设主体希望自己可以选择如何执行一个行动，这也是非确定性行动或者执行替代路径的动机。非确定性实际上意味着主体没有关于系统行为的完整信息，或者很难获取或者存储此类信息。此外，即使与不同的主体相关联的具体行动也可以由复杂的行动组成，这一性质对于描述多主体的团队协作非常有利。

由于主体具有智能，它们必须对世界有一些了解，或者至少有一些信念或者知识。可以把主体的信念（或者知识）看作是主体相信（或者知道）的公式集。因为主体在其活动中执行行动和“学习”，所以在信念（或知识）与行动之间必须有某种相互依存的关系。获得关于主体信念或者知识的信息，其实是主体头脑中的某种行动。主体的信念和知识通过动态信息测试算子进行整合，该算子确认主体的信念（或知识），而不是像命题动态逻辑PDL中的经典测试算子那样确认实际状态的性质。

（一）BBDDLL逻辑的语言

BDL逻辑语言由四种不相交的成分组成：主体集Ã、抽象行动集Π1、具体行动集Π2和公式集Σ。抽象行动可以是原子行动，也可以是复合行动。具体行动是“具体主体执行的”抽象行动，它们也可组合成复杂的具体行动，这些行动的语义必须包含主体的非确定性。通常，用公式描述多主体系统的性质。

使用如下集合和逻辑联结词可定义BDL逻辑的语言L：命题变元的可数集Δ={p，q，r，…}、抽象原子行动变元的可数集Π0={a，b，c…}，以及主体变元的可数集Ã={i，j，k，…}。逻辑联结词包括经典联结词，→和⊥，信息测试算子，行动公式的标准命题动态逻辑PDL的联结词∪（程序不确定性选择算子）、；（程序的序列合成算子）和*（程序迭代算子），以及动态模态算子[]（box算子）。抽象行动、具体行动和公式可以同时使用归纳的方式加以定义，使得抽象行动集Π1、具体行动集Π2和公式集Σ是满足以下条件的最小集合。 ∩

（1）Π0⊆ Π1，Δ{⊥}⊆ Σ；

（2）如果φ∊Σ并且α，β∊Π1，那么φ，α*，α∪β，α；β∊Π1

（3）如果α∊Π1并且i∊Ã那么αi∊Π2；

（4）如果α，β∊Π2那么α*，α∪β，α；β∊Π2；

（5）如果φ，ψ∊Σ并且α∊Π2那么φ→ψ，[α]φ∊Σ。

﹁，⊤，^，ˇ，↔这些公式联结词可以用通常的方式由经典联结词→和⊥加以定义。diamond算子〈〉是box算子[]的对偶，即〈α〉φ↔﹁[α]﹁φ。信念算子Bi定义为模态算子(⊤?)i。公式Bip读作“主体i相信p”。

公式集Σ的任意子集在分离规则、概括规则和替换规则下封闭。

分离规则：如果φ且φ→ψ成立，那么ψ成立，即φ，φ→ψ⊢ψ。

概括规则：如果φ成立，那么[α]φ成立，即φ⊢[α]φ。

其中φ，ψ∊Σ并且α∊Π2。

注记：（1）如果变元x在φ中的所有出现都被ψ中的项s替换，那么公式ψ是用s替换x时φ的替换实例，记作ψ=φ{s/x}。（2）令a是原子抽象行动，j是具体行动α中的主体变元，那么在a替换aj的情况下，公式ψ是φ的替换实例，记作ψ=φ{α/aj}。（3）对于任意两个公式集Γ和Λ，Γ⊕Λ表示同时包含Γ和Λ的最小逻辑；具体地说，PDL和S5融合后的逻辑记作：PDL⊕S5。

（二）BBDDLL逻辑的语义

BDL模型是四元组M=〈S，f，g，⊨〉的克里普克模型，使得M1=〈S，f，⊨〉是PDL模型，M2=〈S，g，⊨〉是S5模型；其中S是一个非空的状态集，f是把每个具体行动a与一个二元关系f(a)关联起来的映射，g是从主体集合到S上的传递关系和欧几里得关系集的映射，⊨是克里普克模型上的真值关系。任何BDL模型都必须满足以下10个条件。对于任何具体行动α和β，映射f应该满足的一般条件是：

(M1)：f(α∪β)=f(α)∪f(β)

(M2)：f(α；β)=f(α)∘f(β)

(M3)：f((α)*)=(f(α))*

这里“∘”表示关系组合，*是关系上的自返传递闭包算子。对于任何抽象行动α、β和主体i，把具体行动与抽象行动联系起来的映射f应该满足的条件是：

(M4)：f((α∪β)i)=f(αi∪βi)

(M5)：f((α；β))i=f(αi；βi)

(M6)：f((α*)i)=(f(αi))*

关于真值关系的标准条件必须为真，其中s表示任意状态，ψ和φ是任意公式，α是任意具体行动：

(M7)：M，s⊭⊥

(M8)：M，s⊨φ→ψ ⇔ M，s⊨φ ⇒ M，s⊨ψ

(M9)：M，s⊨[α]φ ⇔ ∀t((s，t)∊f(α)⇒ M，s⊨φ)

信息测试算子的语义为：

公式φ在模型M的状态s中有效，记作M，s⊨φ；如果φ在模型的所有状态下都有效，那么就说φ在模型M中是有效的。BDL逻辑是在所有BDL模型中有效的公式集。

三、BDL逻辑的公理化、可判定性和复杂性

通过如下公理、分离规则、概括规则和替换规则，可以给出BDL逻辑的希尔伯特式公理化系统。BDL逻辑包含如下公理：

(A1)经典命题逻辑的公理

(A2)无测试行动的命题动态逻辑PDL的类似公理：

(A2.3)[ai；bj]p↔[ai][bj]p

(A2.4)[(ai)*]p→p^[ai]p

(A2.5)[(ai)*]p→[ai][(ai)*]p

(A2.6)p^[(ai)*](p→ [ai]p)→ [(ai)*]p

(A3)信念算子的K45公理：

(A3.1)Bip→BiBip

(A3.2) ﹁Bip→ Bi﹁Bip

(A4)抽象行动与具体行动之间的对应公理：

(A4.2)[(a；b)i]p↔[ai；bi]p

(A4.3)[(a*)i]p↔[(ai)*]p

(A5)信息测试算子公理：

由于BDL逻辑是由命题动态逻辑PDL和模态逻辑S5融合而成，融合逻辑系统可以继承其组成逻辑的诸多优良性质，如可靠性、完全性、有穷模型性质和可判定性[19][20]。由于PDL和S5都具有这四个性质，因此BDL逻辑也具有这四个性质。利用模态逻辑和动态逻辑方法，可以给出BDL逻辑这四个性质的证明；但是由于新的信息测试算子的存在，只需对其证明进行必要的修改即可，因此本文只给出其结论，并不给出这四个性质的详细证明。

定理 11（完全性）：上述BDL公理系统对于所有BDL模型类是完全的。

现在讨论BDL逻辑的有用扩展。在一些多主体系统中的一些主体比BDL逻辑中的主体具有更高的智能。通常要求主体的信念能够充分反映系统的性质，这时，主体的信念实际上变成了知识。为了使主体具有这种额外智能，需要在BDL逻辑中添加T公理：Bip→p，这时的BDL逻辑中信念算子Bi就是S5系统中的模态词，代表知识算子。此外，还要求主体信念具有一致性，该性质可以通过在BDL逻辑中添加D公理来表示：Bip→﹁Bi﹁p。

在对智能主体进行建模时，一个关键问题就是弄清信息态度和行动之间的联系。信息态度和行动之间最广为人知和最自然的联系是无学习和完美回忆（perfect recall）[21]。无学习性质通常由NL公理模式来表示：[ai]Bip→Bi[ai]p，其中Bi通常表示认知算子；其意思是：主体i事先知道其行动的结果，即：不需要学习。完美回忆通常由公理模式PR来表示：Bi[ai]p→[ai]Bip；它表示在执行一个行动之后，主体的知识（有时是信念）具有持久性。

还可以要求这些模型具有如下性质：

等价性：∀igi是一个等价关系

持续性：∀i∀s∃t(s，t)∊gi

左交换性：∀i∀α(gi∘f(αi)⊆f(αi)∘gi)

右交换性：∀i∀α(f(αi)∘gi⊆gi∘f(αi)

定理 22（完全性）：令L是由公理T、D、NL和PR的任意组合而形成的BDL逻辑的扩展系统，那么L相对于“具有等价性、持续性、左交换性和右交换性的相应组合的”所有模型类而言，都是完全的。

定理 44（可判定性和复杂性）：由公理T、D、NL和PR的所有可能组合构成的BDL逻辑的所有扩张逻辑的可满足性问题，以及BDL逻辑本身的可满足性问题，在EXPTIME（确定性指数时间）中是很难判定的，但是在2EXPTIME（即2倍确定性指数时间）内是可以判定的。

现在在BDL⊕T中定义（完全测试）命题动态逻辑PDL的一个翻译。选择一个主体，比如主体i，然后定义从PDL公式到公式集Σ的映射h如下：

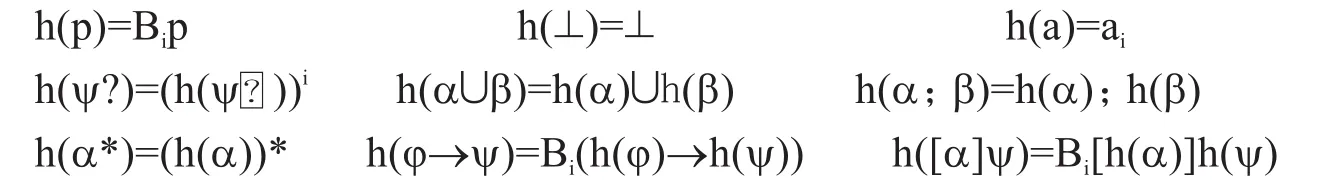
下面的定理表明，翻译函数h在两个方向上都保持了公式的真值。

定理 55：对于任意命题动态逻辑PDL公式φ，φ∊PDL，当且仅当，h(φ)∊ BDL⊕ T。

施归纳于公式集Σ中公式的结构，即可证明定理5。或者参照张晓君（2017）[1]102-103中的等级BDI逻辑到PDL的翻译函数的类似证明亦可得证。

没有（经典）测试算子的命题动态逻辑PDL是BDL逻辑的一个子逻辑。因此，BDL逻辑可以对BDL逻辑中的简单程序（如while程序）进行推理。为了能够对任何程序进行推理，定理5对BDL逻辑进行了最小强化。

信息测试行动最重要的特征是：可以使主体的内隐信念得到显性化。确认公式的行动和确认公式的否定的行动都可以为主体提供信念（知识），这种组合行动是一种信息行动[23]。任何确认公式及其否定公式的行动都是“二选一测试”（alternative test）[24]。该测试的特点是：被测公式的真假不应受到实际测试行为的影响，即测试的结果应与被执行的测试的状态相对应，这一特性称为真实性（truthfulness）

“二选一测试”具有最小更新性质，其意思是：这种测试不能从“与测试行为无关的主体的信念集中”添加或者删除公式。这意味着，如果一个主体在下载文件之前认为“北京是中国的首都”，那么在文件下载后她仍然会认为“北京是中国的首都”。

四、结束语

本文的研究表明：（1）把模态逻辑S5系统与命题动态逻辑PDL进行融合，并对PDL逻辑中的测试算子的语义和形式系统进行重新描述，可以得到动态信念和知识的多主体逻辑BDL；这种新的信息测试算子能够使得主体的动态信息（如知识）、这些动态信息的真实性和信念得以保持；（2）BDL逻辑是信念-愿望-意图逻辑BDI（其基础系统是PDL逻辑）的变种，采用“能够对抽象行动和具体行动加以区分的”新的行为表示方法，可以达到对多主体环境下的动态信念和知识建模的目的；（3）BDL逻辑不仅可以表达共同的信念和共同的知识，而且这种带有信念和知识模态词的多主体逻辑比PDL逻辑具有更强的表达力；（4）BDL逻辑的复杂性在2EXPTIME（即2倍确定性指数时间）之内；（5）BDL逻辑不仅可以表征多主体环境下信念或者知识的自然属性，而且还可以表征信念或者知识与行动之间的交互。

未来的工作可以考虑：如何在BDL逻辑框架中，对“能够对知识进行推理的”其他逻辑进行适当的公理化？这些逻辑的可判定性如何？