斜顶直帮回采巷道围岩应力分布研究

李世辉，李世领

(淮南矿业集团，安徽 淮南 232001)

0 前 言

回采巷道围岩应力分布是回采巷道支护设计的重要依据。斜顶直帮巷道以其不破顶的优点在倾斜煤层开采中得到了广泛应用。针对受力条件，圆形和椭圆形断面巷道受力条件较好，其巷道围岩稳定性较高，直墙半圆拱、直墙三心拱等弧顶断面巷道次之，矩形、梯形、斜顶直帮和斜顶斜帮等巷道最差。其中，斜顶直帮巷道受力情况尤为复杂，同时，由于斜顶直帮巷道断面的不规则性，其应力分布解析解求解一直是一个难题。

众多国内外学者[1-4]运用复变函数法求解了矩形巷道围岩应力分布的解析解，分析了侧压系数、巷道面积、巷道跨高比等因素对矩形巷道围岩应力分布和应力集中系数分布的影响规律；袁林等[5]和李明等[6]结合矩形巷道围岩应力求解方法和粘弹性相关理论，求出了矩形巷道围岩在广义开尔文本构模型和鲍尔丁-汤姆逊本构模型情况下的应力分布随时间的演化规律。

现有文献对椭圆形、矩形等规则断面巷道围岩应力分布的研究较为充分，但是缺少针对斜顶直帮巷道的理论研究。本文参考前人的研究成果，使用Laurent级数近似斜顶直帮巷道围岩区域到复平面上单位圆内的共形映射函数，然后运用复变函数法求出斜顶直帮巷道围岩应力分布解析解。以潘三煤矿某工作面回风巷为工程背景，分析了斜顶直帮巷道围岩主应力和主应力集中系数分布特征。

1 斜顶直帮巷道围岩应力分布求解

不考虑巷道围岩的自重应力，斜顶直帮巷道所受围岩应力条件用垂直应力σV、水平应力σH和剪应力τ表示，斜顶直帮巷道受力如图1所示。

图1 斜顶直帮巷道受力示意图

本文运用科学计算软件编程，求解复系数Cn。

根据实部与虚部相对应的原则，z平面上点的坐标与ξ平面上点的坐标之间的对应关系为：

(1)

围岩应力可由复平面上的2个复位势函数φ(Z)和ψ(Z)确定：

(2)

式中，复变函数φ0(ξ)和ψ0(ξ)表示在定义域内满足Cauchy-Riemann条件的解析函数，可展开为Taylor级数；σ1和σ3为巷道所受应力条件的最大主应力和最小主应力；α1和α3为最大主应力σ1和最小主应力σ3与x轴的夹角。

通过边界条件可求得解析函数φ0(ξ)和ψ0(ξ)，具体求解过程见参考文献[1-3]，这里不再赘述。

然后可通过式(3)求得围岩应力分布。

(3)

由斜顶直帮巷道围岩应力分布的求解过程和求解结果可看出斜顶直帮巷道围岩应力分布与巷道围岩的弹性模量和泊松比无关，只与巷道断面形状和巷道应力条件有关。

2 应力分析

煤层倾角在22°～35°，平均24°，为典型的倾斜煤层。回风巷沿煤层顶板掘进，形成典型的斜顶直帮巷道。为方便对巷道围岩的应力分析，对巷角进行编号，回风巷断面如图2所示。依据地应力测试结果，取垂直应力σV=13.2 MPa，水平应力σH=19.5 MPa，剪应力τ=-0.2 MPa。

图2 回风巷断面(单位：mm)

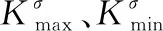
(a)最大主应力集中系数

由图3(a)可知，在巷道角点处，最大主应力和最大主应力集中系数达到最大值，最大主应力集中系数最大值超过了2.5。与其他巷角相比较，在巷角A处，表明在巷角A处，最大主应力集中系数取值最大且应力集中范围最广。在巷角D处，最大主应力集中系数取值最小且应力集中范围最小。高帮围岩浅部的最大主应力集中系数小于低帮浅部，如图3(a)所示。

由图3(b)可知，斜顶直帮巷道最小主应力集中系数整体呈现花形分布。在巷道角点处，最小主应力集中系数达到了最大值，最小主应力集中系数最大值超过了2.5。与其他巷角相比较，在巷角A处，最小主应力集中系数取值最大且应力集中范围最广。在巷角D处，最小主应力集中系数取值最小且应力集中范围最小。巷道表面的最小主应力集中系数为0。在两帮和顶底板围岩中部，最小主应力集中系数较小，如图3(b)所示。并且高帮围岩内的最小主应力降低区分布范围远大于低帮。

由图3(c)可知，在巷角处，最大剪应力集中系数达到最大值，最大剪应力集中系数最大值超过了5。与其他巷角相比较，在巷角A处，最大剪应力集中系数取值最大且应力集中范围最广。在巷角D处，最大剪应力集中系数取值最小且应力集中范围最小。顶底板最大剪应力集中系数整体大于两帮。高帮区域面积大于低帮，表明高帮最大剪应力集中系数整体大于低帮。由此可知，巷角是斜顶直帮巷道中稳定性最差的部位，且巷角A相对于其他巷角稳定性更差，巷角D稳定性相对于其他巷角稳定性较好。两帮较顶底板稳定，低帮较高帮稳定，且高帮失稳区范围和失稳区深度远大于低帮。因此，巷道顶板的支护强度应当大于两帮，高帮的支护强度大于低帮。同时，应当加强对巷角的支护强度，尤其是巷角A。

3 结 论

1)斜顶直帮巷道的共形映射函数的最大绝对误差为14.9 mm，平均绝对误差为1.5 mm，四个巷角的曲率半径分别为11.4、34.5、36.5和93.3 mm。斜顶直帮巷道的共形映射函数精度很高，可用于斜顶直帮巷道应力分布求解。

2)斜顶直帮巷道围岩最大主应力、最小主应力、最大剪应力的集中系数的最大值均出现在巷角处，主应力集中系数最大值分别超过2.5、2.5和5，巷角是斜顶直帮巷道的薄弱部位。

3)顶底板最大剪应力集中系数整体上大于两帮，两帮较顶底板稳定；高帮最大剪应力集中系数整体上大于低帮，且最大剪应力增高区面积远大于低帮，低帮较高帮稳定。

[ID:012879]