基于二子空间协同训练算法的半监督软测量建模

罗顺桦，王振雷，王昕

（1 华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237；2 上海交通大学电工与电子技术中心，上海 200240）

引 言

在工业生产过程中，及时跟踪和有效预测主导变量，例如产物的质量指标，对保持生产过程的稳定性与可靠性极为重要。为了解决主导变量难以直接测量的问题，软测量技术利用与主导变量密切相关的辅助变量，如易于测量的液位、温度、进料量等，构建数学模型，对主导变量进行在线预测。因此，相比于价格高昂且滞后大的在线仪表分析法，拥有经济可靠、动态响应迅速等优势的软测量技术在工业生产中得到了广泛的应用[1-2]。

目前，常用的软测量建模技术有基于过程反应机理建模[3]、基于数据驱动建模[4-5]以及混合建模方法[6]。不同于需要掌握复杂工艺机理的机理建模，基于数据驱动的软测量建模技术仅需利用输入输出等过程数据获取辅助变量与主导变量之间的数学关系，常用的实现方法有回归分析建模[7]、支持向量机(support vector machines,SVM)建模[8-10]以及人工神经网络[11-12]等。机器学习中将同时包含辅助变量和主导变量的数据，即输入和输出的数据称为有标签数据；只包含辅助变量而缺失主导变量的数据称为无标签数据。典型的基于数据驱动的软测量建模过程是有监督学习，需要大量的有标签数据。在很多工业生产过程中，相比于大量易于获取的辅助变量数据，主导变量数据的获取通常依靠实验分析以及专业知识技术，大量时间与资金的投入使获取主导变量数据的成本随之增加，这将导致软测量建模中的输入输出数据失衡，模型拥有有限的有标签数据，从而极大影响了软测量模型的预测可靠性和系统的泛化能力。

不同于有监督学习，半监督学习[13-15]利用大量的无标签数据并辅助少量有标签数据进行模型的训练，通过捕获无标签数据中的潜在信息，提升学习性能。根据方法的不同，半监督学习方法主要分为四种，即基于生成式模型的方法(generative models)[16]、半监督SVM 方法(transductive support vector machines)[17]、基于图的方法(graph-based semi-supervised learning)[18]和协同训练算法(co-training)[19]。

对比于其他的半监督学习方法，协同训练算法简单高效且理论比较完备，没有对数据结构的特殊要求。其基本原理为：首先使用有标签数据集建立两个具有差异性的学习器，并在模型训练过程中不断挑选无标签数据到对方学习器的数据集中，直到满足指定条件。通过捕获无标签数据中的有效信息，从而实现模型稳定性与可靠性的进一步改进[20]。Pierce 等[21]运用带有人为纠正的协同训练算法挑选无标签数据，提高基本名词短语的识别能力。Steedman 等[22]利用未经处理的句子作为无标签数据，使用协同训练算法提高语法分析器的预测能力。Zhou 等[23]挖掘未标记数据的信息，进而提高基于内容的图像检索能力。为了解决协同训练算法中的多视图问题，Goldman 等[24]提出不需要充分冗余视图的算法，该算法思想是两个或多个标准的监督学习算法可能在标记的数据中检测到不同的模式，从而生成两个不同的分类器以进行协同训练的方式来增强分类器性能。但由于使用交叉验证的方式挑选无标签数据，因此该方法会产生巨大的计算开销，同时仅适用于有标签数据较多的情况。Zhou 等[25]提出了更为简单与便于应用的“三体训练法(tri-training)”，该算法通过建立三个分类器以解决对标记置信度的显式估计问题，从而提高模型的泛化能力。但在多数分类器预测错误的情况下，将会在迭代中挑选不合适的无标签数据，从而导致模型的预测性能下降。

早期的半监督学习研究主要聚焦在分类任务上,直到Zhou等[26]提出了协同训练回归算法(CORGE)，设计出适用于回归任务中的标记置信度估计，并将协同训练算法应用到软测量技术上。Bao等[27]提出将数据集在变量维度上均分成两组数据，并结合偏最小二乘算法(PLS)进行回归训练的协同训练偏最小二乘模型。李东等[28]将有标签数据按照奇偶分组的方式分成两份，结合递归PLS(RPLS)和递归bp(RBP)建立半监督异构自适应软测量模型co-traning RPLS-RBP。

利用两组具有显著差异性的数据集进行协同训练建模，亦是协同训练回归中的重要方向[29]。然而目前的研究较少涉及该方向，缺乏利用数据自身属性与特征分析对数据集进行分类的指导方法，数据集分组的随机性与不确定性较强，致使数据信息的分布混乱，模型难以聚焦并挖掘出数据自身的特性，学习器之间存在严重的训练特性交叉重叠现象，从而影响协同训练模型的预测精度。

为此本文提出一种基于二子空间协同训练算法的半监督软测量建模方法。该模型依据辅助变量自身与主成分子空间PCS 和残差子空间RS 两个特征子空间的相关性程度，将数据变量拆分成两个具有分歧性的数据集，从而进行协同训练，共同用于对主导变量的预测。因此，该模型不仅在数据降维中去除了冗余信息和噪声以实现重要变量的提取，并在分组中同时考虑了PCS与RS的各自局部特征，最终拆分为两组相互独立分歧的数据集。最后通过乙烯精馏塔塔顶乙烷浓度软测量建模和TE 平台仿真验证本文所提模型的有效性。

1 背景知识

1.1 主成分分析法（PCA）

主成分分析方法(principal component analysis，PCA)是一种使用最广泛的数据特征提取和降维算法。在软测量建模中，对辅助变量进行特征提取，能有效地去除冗余信息、去除噪声。PCA 的主要思想是将n维特征映射到k维特征空间(n＞k)，在降维的同时保留较多原始数据的信息。

给定一组n维样本X={xi}m i=1，m为样本个数，其降维过程如下。

(1) 对样本X进行标准化处理得到X̂，其中均值为：

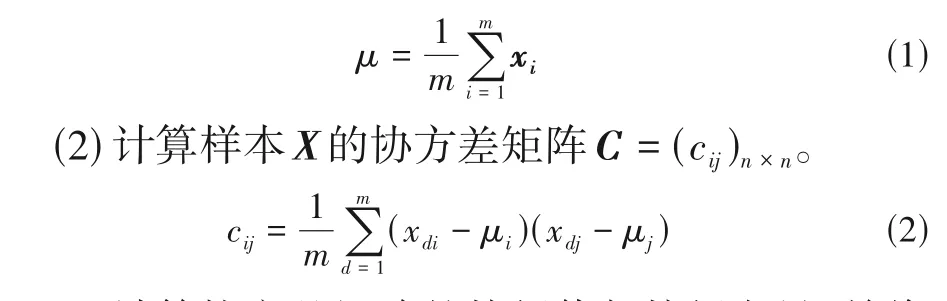
(3)计算协方差矩阵的特征值与特征向量，并将特征值由大到小进行排列，即为λ1≥λ2≥···≥λn，因此特征值所对应的特征向量构成矩阵Φ。

(4) 根据特征值累计贡献率的要求α选择降维后的维数k，假设α=80%。

(5) 特征向量q1,q2, ···,qk构成主成分子空间PCS，而特征向量qk+1,qk+2, ···,qn构成残差子空间。

(6)将X̂进行低维映射得到低维数据Y。

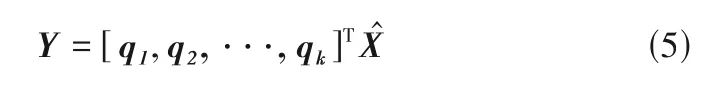
1.2 K近邻算法（KNN）

KNN (K-nearest neighbour) 算法是一种较为成熟的惰性学习方法，既可运用在分类任务中，也可以用于回归问题上。不同于神经网络模型，作为一种非参数的建模方法，KNN 无须单独的训练阶段而能快速地进行回归预测，从而节省大量的时间，更加适用于拥有大量无标签数据的半监督学习。KNN 的主要思想为：对于每一个新数据x，使用对应的距离度量，找出基于x的k个最相近的样本。由于不同距离的k个样本对x将产生不同的权重影响，因此x的最终预测值为k个样本输出的加权平均值。其中常用的距离度量有：

(1)欧式距离

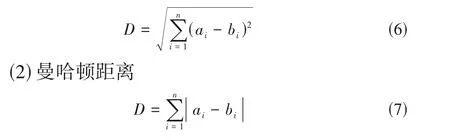
其中，a和b表示n维空间中的两个点。

1.3 协同训练算法（COREG）

协同训练算法能有效地利用无标签数据中所包含的有效信息，进而改善与提升模型的相关性能，是半监督学习中常用的方法之一。协同训练算法(COREG)挑选置信度高的无标签数据到数据集中，实现模型的有效更新和改进。

COREG的具体算法步骤如下：

设L={X,Y}={(x1,y1),(x2,y2), ···,(xl,yl)} 表示有标签数据集，U表示无标签数据集，其中X为辅助变量输入数据，Y为主导变量输出数据，l为有标签数据的个数。令L1=L2=L作为模型的两组有标签数据集，使用带有不同距离指标系数p的KNN 算法分别建立出两个初始回归模型h1和h2。随后，取i等于1和2，以计算第i个模型的相关参数。

(1)计算有标签数据集Li的均方根误差Ri，针对每个无标签数据xu，使用hi计算其预测值yu。

(2) 将新样本组合(xu,yu)添加到原数据集Li中组成新数据集Li'，建立新的回归模型hi'，并计算Li'的均方根误差Ri'。其中u为无标签数据的个数。

(3) 计算Ri和Ri'的差值Δxu作为每个无标签数据xu的置信度，从中挑选置信度最大值的无标签数据xu，组合成新的有标签数据(xu,hi(xu))交叉放置到数据集中，即(xu,h1(xu))放入L2，(xu,h2(xu))放入L1。其中置信度的公式为：

2 基于TSCO-KNN的软测量模型

2.1 二子空间（TS）

二子空间(two subspace，TS)是一种依据变量特性，将模型中的数据变量拆分为两个独特的子空间的分块方法，形成两个具有差异性的数据集。在传统的PCA对数据进行降维时，数据被分解为两个特征子空间，分别为主成分子空间PCS 和残差子空间RS。TS方法首先定义辅助变量与PCS及RS的相关性指标，确定各辅助变量与这两个特征子空间相关性系数，随后通过相关性的分类调整，将辅助变量进行分割，从而形成两个具有差异性的辅助变量子空间。

(1)P1R0子空间：即仅与PCS 相关而与RS 不相关的辅助变量所构成的子空间；

(2)P0R1子空间：即与PCS 不相关仅与RS 相关的辅助变量所构成的子空间。

其中，1 表示相关，0 表示不相关。二子空间的形成具体步骤如图1所示。

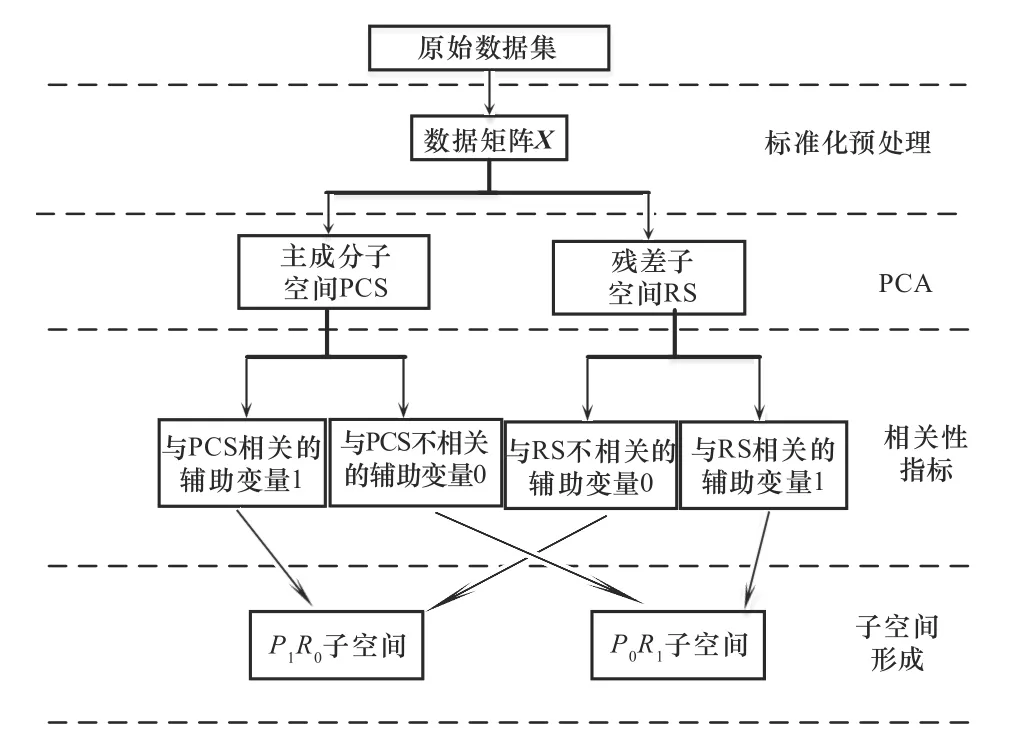
图1 二子空间的构建图Fig.1 Construction of two subspace

如图1所示，数据矩阵X经过PCA 降维后，会分别形成主成分子空间PCS 和残差子空间RS。这里使用复相关系数定义各辅助变量与PCS 和RS 的相关性指标。

在计算得到各辅助变量xi对应的相关性系数αi和βi后，由于缺乏先验知识，本文利用相关性系数的均值作为阈值，以区分与PCS和RS相关或不相关的辅助变量，即

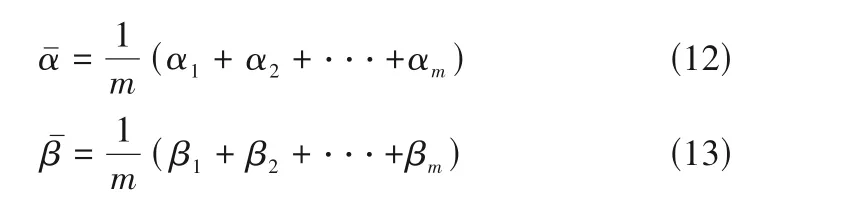
可以看出，相比于囊括全部变量的原始数据空间，使用二子空间进行划分而得的单个子空间拥有着数量更少的变量，且这部分变量代表了原始空间中的大部分特征信息。因此，二子空间方法在起到数据降维作用的同时，也充分地保留了原始数据的信息，防止了潜在信息丢失的问题。同时，根据上述相关性规则划分所得的子空间，包含着最具有密切关联的辅助变量，且各辅助变量仅存在于二子空间之一中，即不会发生变量重叠的问题，由此二子空间彼此之间具有最大限度的差异性。在协同训练中，要求两个数据集中数据具有相同的变量维度，然而根据TS 方法得出的两个子空间中的数据的变量数有可能不完全相同（如P1R0子空间数据变量数为k1，P0R1子空间数据变量数为k2，假设k1＞k2），此时需要根据相关性系数，在变量数较多的子空间中，将相关性系数较低的变量剔除，以达到k1=k2。由于变量的多样性，从目前的仿真结果看来，并未出现k1比k2多很多或者k2比k1多很多的情况。若在未来的研究中出现此类情况，可探索新的定义阈值的方法，以使两个子空间中的数据变量相对均匀。

2.2 基于二子空间协同训练模型TSCO-KNN

协同训练算法要求算法中的两个模型具有一定的差异性。在PCA 降维中，PCS和RS都是原始数据经过线性投影所得，而辅助变量在投影过程中拥有着不同的投影权值，导致即使大部分的原始数据的信息保留到PCS中，但仍有小部分原始数据信息遗留在RS中。二子空间的方法利用数据自身的分布与特性，挖掘出数据与两个特征子空间之间的潜在关系，通过数据集的拆分方法，形成两组具有差异性的数据集，从而更加有效准确地挑选无标签数据进行协同训练。

二子空间协同训练模型的主要步骤如下：首先，使用二子空间TS 方法，从辅助变量自身特性出发，确定各辅助变量与PCS及RS两个特征子空间相关性程度，通过相关性指标对辅助变量进行分割，由于辅助变量的独立分布不重叠，原有的有标签数据集L将拆分为两个具有显著差异性的子空间分块，即P1R0子空间L1={X1,Y1}和P0R1子空间L2={X2,Y2}。使用KNN算法对两个子空间数据集建模，分别得到两个独特且拥有显著差异性的回归器模型hi(Li)，其中i= 1,2。并通过模型hi(Li)计算出其对应的均方根误差Ri。接着，针对每个无标签数据xu，使用hi(Li)计算其预测值yu，并将新样本组合(xu,yu)添加到原数据集Li中组成新数据集Li'={Li∪(xu,yu)}，进而建立新的回归模型hi'(Li')，并计算Li'的均方根误差Ri'。最后计算Ri和Ri'的差值Δxu作为每个无标签数据xu的置信度，对应置信度最大值的无标签数据xu将被挑选出来，组合成新的有标签数据(xu,hi(xu))交叉放置在L3-i中。

当满足停止条件，中止训练后，使用最终的有标签数据建立两个新的回归模型，且两个新模型的回归预测值作为最终的预测值。

基于二子空间协同训练模型TSCO-KNN 的步骤如表1所示。

表1 基于二子空间协同训练模型TSCO-KNN的算法流程Table 1 Algorithm based on two-subspace collaborative training model TSCO-KNN

3 仿真应用

为了验证本文所提基于二子空间协同训练算法的预测性能，分别对田纳西-伊斯曼过程（TE process）的成分E 和乙烯精馏塔塔顶乙烷浓度进行软测量建模和比较。模型的评估指标参数为以下三种，通过这些指标衡量回归预测算法的性能。

(1)均方误差(MSE)。通过计算观测值和真值差值的平方和与样本个数m比值，MSE 可以评价数据的变化程度，MSE 的值越小，说明预测模型对实验数据的描述具有更好的精确度。公式为：

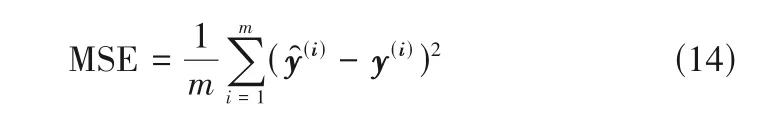
其中，m表示观测个数；y̑(i)表示第i个观测值；y(i)表示第i个真值。

(2)均方根误差(RMSE)。通过计算观测值与真值偏差的平方和与样本个数m比值的平方根，均方根误差可衡量观测值与真值之间的偏差，使结果的单位和数据集一致，从而避免出现量纲问题。公式为:

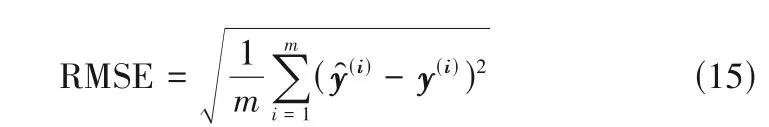
(3)平均绝对误差(MAE)。通过计算观测值和真值的绝对值之和与观测个数的比值，平均绝对误差反映出观测值误差的实际情况。公式为：

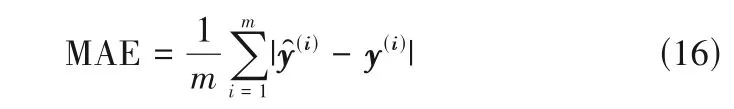
为了验证本文模型的优越性，将其与cotraining KNN(1)模型和co-training KNN(2)模型进行对比分析，三组模型所用相近的样本k均为5。cotraining KNN(1)模型为经典的COREG 模型，使用欧式距离和曼哈顿距离作为不同的距离指标系数；cotraining KNN(2)模型将数据在变量维度上进行对半拆分，使用前一半变量和后一半变量分别建立回归模型。其中co-training KNN(2)模型与TSCO-KNN模型均使用欧式距离作为距离指标系数。另外，训练的循环次数为80，原因在于对应KNN这类传统学习算法，当训练样本个数达到一定数量后，继续增添训练集样本个数难以对模型精度有显著提升，反而会造成一定的时间浪费。同理在实际工业生产过程中，如果每次循环都从大量的无标签样本中选取最优样本，时间损耗将难以估计。因此，可根据实际情况设置循环次数和无标签数据样本范围。

3.1 TE软测量仿真

依据实际化工反应过程，美国Eastman 化学公司开发了具有开放性和挑战性的化工模型仿真平台Tennessee Eastman(TE)仿真平台，其产生的数据具有时变、强耦合和非线性特征，广泛用于测试复杂工业过程的控制和故障诊断模型[30]。

TE 过程共包含着12个控制变量和41个测量变量，其中测量变量为A 进料、反应器压力、气提器温度等22个过程变量，以及流6、9、11中的19个成分变量。本文使用22个过程变量作为辅助变量输入，流6成分D、E、F作为主导变量输出。将原有训练集和测试集数据集进行合并，取前1000个样本数据作为新训练集，剩余460个样本数据作为新测试集。在仿真实验中，分别从训练样本中随机选取数据集中的10%、20%和50%作为有标签数据（即100组，200组，500 组），剩余的训练样本对输出变量进行覆盖，作为无标签数据以进行模型的训练。训练的循环次数为80。当训练结束后，使用模型对460 组测试样本进行对主导变量的数值预测，以评估模型的预测性能。为了更加清晰地观察实验结果，图2 只选取了前200个样本点进行展示。

以有标签数据比例为50%为例，由表2 和图2的仿真实验结果可以得出：对于流6 成分D、E、F，co-traning KNN(1)与co-traning KNN(2)的预测数值维持在小幅度范围内变化，在大部分时间点上数值都较为严重地偏离真实值，无法跟踪变化波动较大的数值。相比之下，TSCO-KNN 模型的预测效果明显好于co-training KNN 模型，大部分的预测值能很好地拟合真实值。其中，以流6 成分E 为例，相比于co-training KNN(1)，本文模型在RMSE 指标上提高了35.37%；在MSE指标上提高了58.22%；在MAE指标上提高了35.78%；相比于co-training KNN(2)，本文模型在RMSE 指标上提高了33.05%；在MSE 指标上提高了55.17%；在MAE指标上提高了34.02%。

图2 有标签比例为50%的co-training KNN(1)、co-training KNN(2)、TSCO-KNN模型效果对比Fig.2 Comparison of the effects of co-training KNN(1),co-training KNN(2),and TSCO-KNN models with a label ratio of 50%

表2 有标签比例为50%下三种模型的性能评估（TE）Table 2 Evaluation（TE）of the three models with a label ratio of 50%

另外，以成分E 为例，图3 表示在不同有标签比例下三组模型的RMSE 值对比。可以看出，在任何有标签数据比例下，TSCO-KNN 模型的性能都远胜于co-traning KNN 模型。而且，随着有标签数据比例的逐渐提高，模型性能提升的幅度也逐渐降低，原因在于使用数量较多有标签数据训练所得的模型已有一定的预测精度，在此基础上利用无标签数据的潜在信息的效果甚微。另一方面，在有标签数据比例变化时，co-training KNN 模型的RMSE 值仅有着微弱的改变，从中推测TE工业过程或适用于其他的回归学习器，使用不同的回归学习器或能产生更好的预测效果。

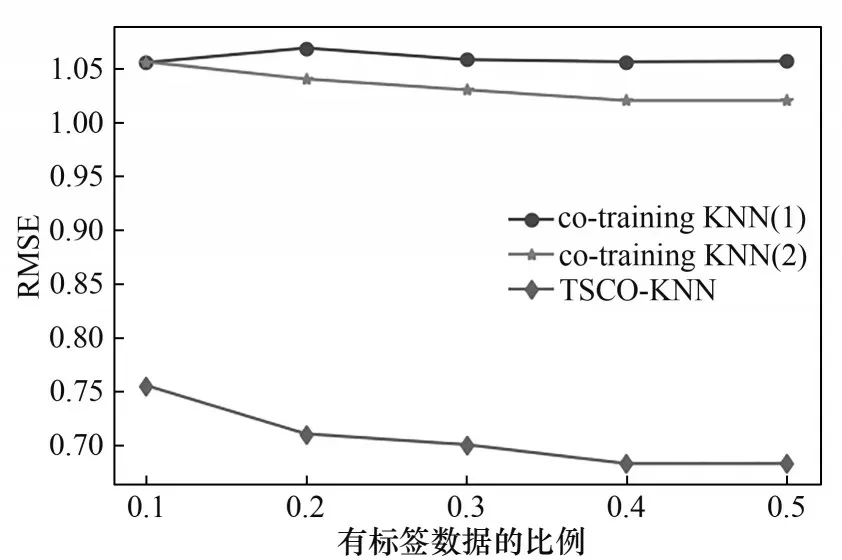
图3 不同有标签数据比例下成分E的RMSE值Fig.3 RMSE values of component E under different labeled data ratios

3.2 乙烯精馏塔塔顶乙烷浓度软测量仿真

本文使用乙烯工业过程中的乙烯精馏塔塔顶乙烷浓度软测量来验证本文所提方法的有效性和优越性。图4 为乙烯精馏塔的生产流程图，该塔主要实现将输入的乙烷、乙烯及微量甲烷和氢气等混合物，分离成为聚合级乙烯（塔顶釆出）和乙烷（塔釜釆出）。塔顶聚合级乙烯产品中乙烷浓度的有效测量和控制是精馏塔操作的关键。

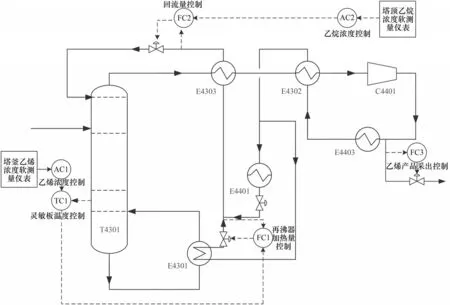
图4 乙烯精馏塔流程图Fig.4 Ethylene distillation tower flow chart

选取乙烯精馏塔塔顶乙烷浓度作为软测量模型的输出；精馏塔的主要过程变量——塔顶压力、塔顶温度、塔底温度、回流量、灵敏板温度等38个变量为辅助变量。

根据实际生产现场的工艺流程，仿真数据为2016 年10 月18 日18 点38 分到2016 年10 月20 日3 点58 分之间的乙烯精馏塔的现场采集数据，共为2000 组。为了验证TSCO-KNN 模型的有效性以及实验结果的可靠性，本文使用不同的有标签数据比例分别进行仿真实验。首先将2000 组数据按照奇偶分组方式均分成两部分，分别为1000组训练样本和1000组测试样本。并在仿真实验中，分别从训练样本中随机选取数据集中的10%、20%和50%作为有标签数据（即100 组，200 组，500 组），剩余的训练样本对输出变量进行覆盖，作为无标签数据以进行模型的训练。当训练结束后，使用模型对1000组测试样本进行对乙烯精馏塔塔顶乙烷浓度的数值预测，以评估模型的预测性能。

由表3～表5和图5、图6的仿真实验结果可以得出：在各种有标签比例下，co-training KNN(1)模型的预测效果存在着较大的偏差，co-training KNN(2)模型的效果比前者稍好，而TSCO-KNN 模型的预测值都更好地跟踪真实值的变化趋势，其预测效果明显好于co-training KNN(1)模型和co-training KNN(2)模型。当有标签比例为10%时，相比于co-training KNN(1)，TSCO-KNN 模型在RMSE 指标上提高了39.51%，在MSE 指标上提高了63.39%，在MAE 指标上提高了35.63%；相比于co-training KNN(2)，TSCO-KNN 模型在RMSE 指标上提高了19.36%，在MSE 指标上提高了34.92%，在MAE 指标上提高了15.30%。当有标签比例为20% 时，相比于cotraining KNN(1)，TSCO-KNN 模型在RMSE 指标上提高了45.90%，在MSE 指标上提高了70.52%，在MAE指标上提高了41.18%；相比于co-training KNN(2)，TSCO-KNN 模型在RMSE 指标上提高了29.34%，在MSE 指标上提高了49.65%，在MAE 指标上提高了25.97%。当有标签比例为50% 时，相比于co-training KNN(1)，TSCO-KNN 模型在RMSE 指标上提高了52.74%，在MSE 指标上提高了77.54%，在MAE指标上提高了49.44%；相比于co-training KNN(2)，TSCO-KNN 模型在RMSE 指标上提高了35.94%，在MSE 指标上提高了58.82%，在MAE 指标上提高了32.57%。同时，随着有标签数据比例增加，两个模型的性能评估参数值都在下降，模型的预测效果逐渐提高，与理论分析基本吻合。

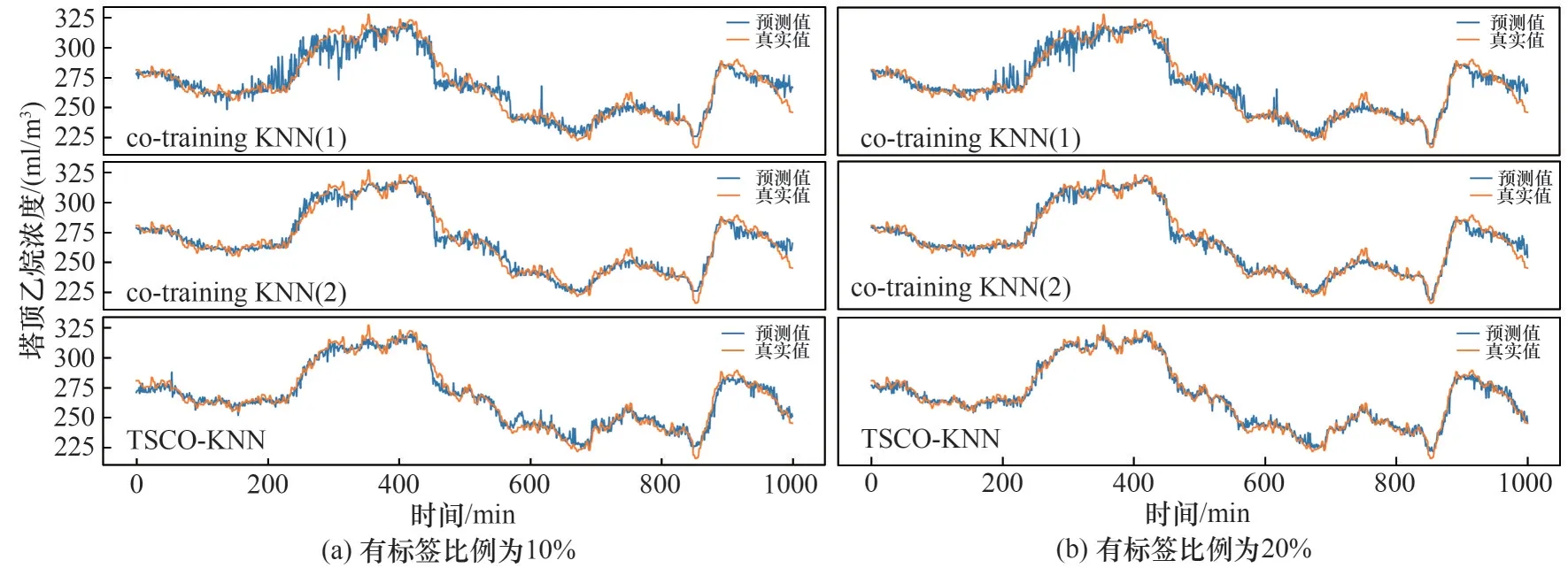
图5 有标签比例为10%和20%下的co-training KNN(1)、co-training KNN(2)、TSCO-KNN模型效果对比Fig.5 Comparison of co-training KNN(1),co-training KNN(2),TSCO-KNN model effects with label ratios of 10%and 20%

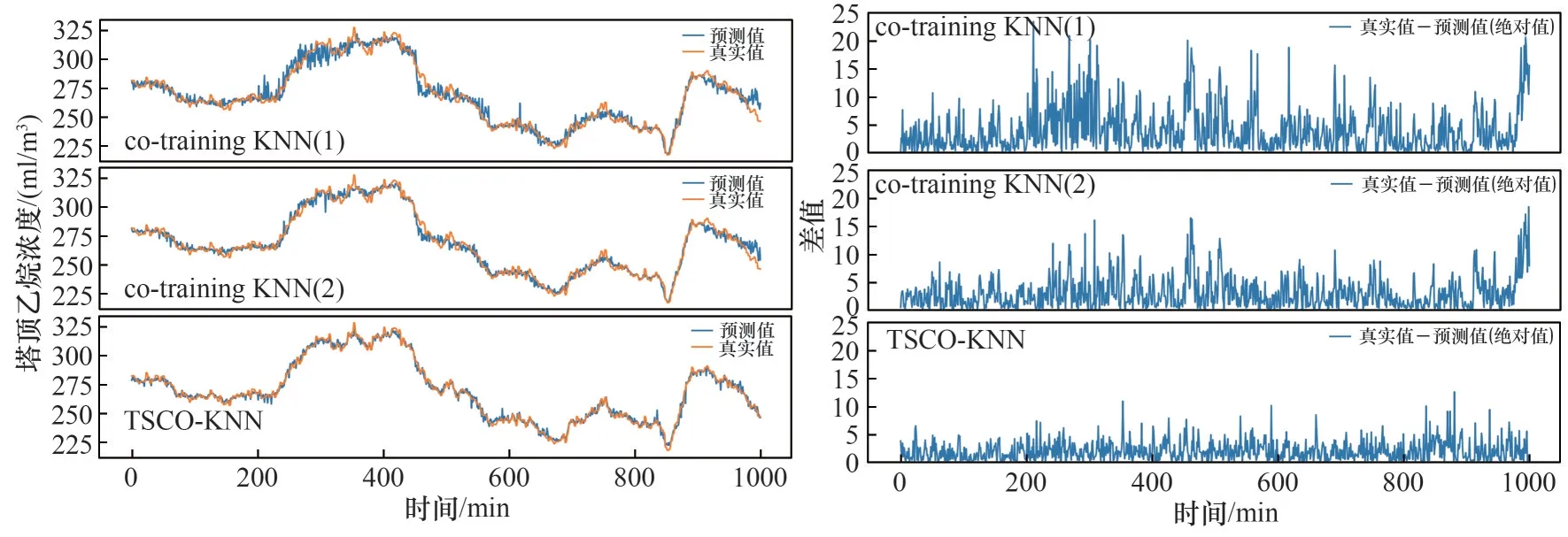
图6 有标签比例为50%下的co-training KNN(1)、co-training KNN(2)、TSCO-KNN模型效果对比和差值对比Fig.6 Comparison of co-training KNN(1),co-training KNN(2),TSCO-KNN model effect and difference with a label ratio of 50%

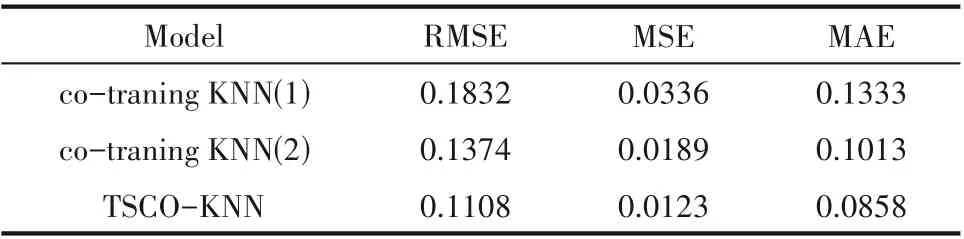
表3 有标签比例为10%下三种模型的性能评估Table 3 Evaluation of the three models with a label ratio of 10%

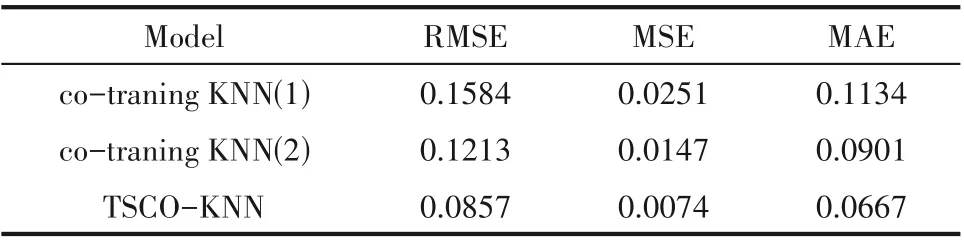
表4 有标签比例为20%下三种模型的性能评估Table 4 Evaluation of the three models with a label ratio of 20%

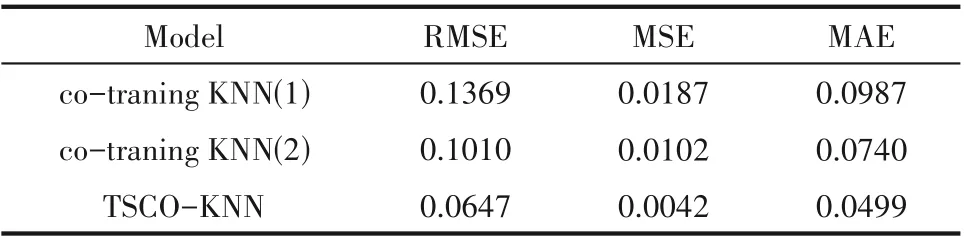
表5 有标签比例为50%下三种模型的性能评估Table 5 Evaluation of the three models with a label ratio of 50%

3.3 仿真分析

上述两组实验数据体现了TSCO-KNN 模型具有更高的预测性能。原因在于传统的协同训练方法，囊括了全部变量的原始数据空间，致使学习器之间存在严重的训练特性交叉重叠。而TSCO-KNN 模型通过二子空间的数据分组后，一方面由于数据的变量维数降低，使用欧式距离作为距离度量的KNN回归学习器能显著地减少预测误差，提高其自身的预测性能；另一方面，由于各自包含着与PCS和RS相关性程度最高的变量，且变量相互独立不重叠，使得两个子空间具有显著的分歧性且各自代表着数据中局部重要特性。然而在不同的实际生产过程中，不同的回归学习器或产生不同的预测效果，未来的研究中会进一步探索最优学习器的挑选和使用。

4 结 论

针对工业过程中有标签数据和无标签数据比例严重失衡的问题，本文在传统的协同训练回归算法的基础上，提出基于二子空间协同训练算法的半监督软测量建模方法。该模型利用数据变量自身特性将数据集拆分为两个具有显著差异性的辅助变量子空间，从而进行协同训练。最后，从乙烯精馏塔和TE 的仿真实验看出，本文的TSCO-KNN 模型在不同标签比例的仿真中都表现出更高的预测性能。